مفاهیم مقدماتی حسابان (بخش چهارم) – به زبان ساده
در بخشهای قبلی از این سری «راهنمای مفاهیم مقدماتی حسابان» دیدیم که میتوانیم فرایند تفکر خود را با قیاسهایی از اشعه ایکس و تایملپس و نمودارها توصیف کنیم.

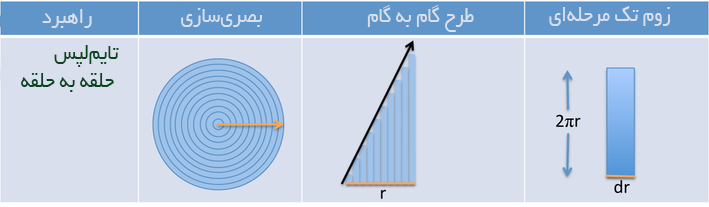
با این حال این روش دشواری برای برقراری ارتباط است. در ادامه اصطلاحهای رسمی ریاضیاتی که برای توضیح مفاهیم شهودی فوق استفاده میشوند را میبینید:
| مفهوم شهودی | نام رسمی | نماد |
|---|---|---|
| اشعه ایکس (جداسازی) | مشتقگیری | d/dr |
| تایملپس (چسباندن به هم) | انتگرالگیری | ∫ |
| جهت پیکان | مشتق یا انتگرال (با توجه به یک متغیر) | dr به معنی حرکت در راستای r |
| آغاز/پایان جهت | کران یا بازه انتگرالگیری | 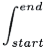 |
| قاچ | عبارت زیر انتگرال (شکلی که باید به هم چسبیده شود مانند یک حلقه) | 2πr |
در ادامه این اصطلاحهای جالب را بررسی میکنیم.
مشتق
مشتق به الگوی برشهایی که هنگام قرار دادن شکل زیر اشعه ایکس به دست میآیند گفته میشوند. مشتق به وسیله خط روند مشخص میشود که میتواند صاف، به صورت صعودی یکنواخت، صعودی/نزولی و یا حالتهای دیگر باشد. با این که مشتق دنباله کاملی از برشها ایجاد میکند؛ اما میتوانیم یک برش منفرد نیز داشته باشیم.
برای مثال تابع را در نظر بگیرید. این تابع مقادیر مربع ممکن را توصیف میکند (1، 4، 9، 16، 25 و غیره) و میتوانیم آنها را روی یک نمودار رسم کنیم. اما میتوانیم همزمان مقدار (f(x را در یک نقطه خاص مانند x=3 نیز به دست آوریم.
مشتق نیز وضعیت مشابهی دارد. به طور رسمی مشتق به الگوی کامل برشهایی که با استفاده از اشعه ایکس به دست میآوریم گفته میشود. با این وجود میتوانیم یک برش خاص را نیز با درخواست مشتق در یک نقطه خاص به دست آوریم. مشتق نیز یک تابع مانند است و ریاضیدانها هر زمان صحبت از مشتق باشد، فرض میکنند که در مورد کل تابع صحبت میکنیم مگر این که یک برش خاص درخواست شده باشد.
اینک سؤال آن است که برای به دست آوردن مشتق به چه چیزی نیاز داریم؟ برای به دست آوردن مشتق تنها به خود شکل و همچنین مسیری که برش مییابد نیاز داریم. در واقع از جمله زیر استفاده میشود: «از فلان الگو با توجه به فلان جهت مشتق بگیر». برای نمونه:
- مشتق یک دایره با توجه به شعاع آن، حلقه تولید میکند (که همواره افزایشی است).
- مشتق دایره با توجه به محیط آن، قاچها را تشکیل میدهد (که اندازه یکسانی دارند).
- مشتق دایره با توجه به محور x، برش را ایجاد میکند (که ابتدا افزایش مییابند و پس از رسیدن به یک اوج دوباره کاهش مییابند).
عمل مشتقگیری به نام دیفرانسیل نیز نامیده میشود، زیرا ما مشغول یافتن تفاوت بین بخشهای متوالی یک شکل در مسیر رشد هستیم. برای مثال همچنان که شعاع یک دایره رشد مییابد، حلقه بیرونی دیسک کنونی نسبت به دیسک بعدی نیز افزایش مییابد.
انتگرال، جهتها و قاچها
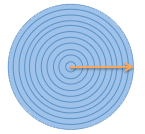
انتگرال به معنی چسباندن دستهای از قاچها در کنار هم (همان رویکرد تایملپس که در این سری مقالات دنبال کردهایم) و اندازهگیری نتیجه نهایی است. برای نمونه ما حلقهها را در کنار هم میچسبانیم و میبینیم که مجموع آنها به صورت πr2 در میآید که مساحت دایره است.
در ادامه مواردی که برای یافتن انتگرال نیاز داریم را ملاحظه میکنید:
- بخشهای مختلف را در کدام جهت باید به هم بچسبانیم؟ برای مثال در راستای شعاع دایره
- چه موقع آغاز کنیم و چه موقع متوقف شویم؟ ما باید از آغاز فلش شروع کرده و نوک پیکان کار خود را خاتمه دهیم. بدین ترتیب در مثال دایره از نقطه مرکزی دایره (0) آغاز کرده و تا پایان یافتن شعاع r کار خود را ادامه میدهیم.
- هر گام چه اندازه است؟ در این مثال دایره هر گام به اندازه یک حلقه است.
البته توصیف فوق تا حدودی کلی است، چون برای مثال بزرگی هر گام انتگرال را معین نکرده است. بنابراین ما باید دقیقاً بیان کنیم که هر مرحله انتگرال باید چه اندازه باشد. این گام به لحاظ فنی «Integrand» نامیده میشود.

در ادامه به چند نکته در مورد متغیر اشاره کنیم:
- اگر ما در راستای شعاع دایره r حرکت کنیم، در این صورت dr بخش کوچکی از شعاع است که در هر مرحله زیر انتگرال قرار میگیرد.
- ارتفاع حلقه به اندازه محیط آن است که برابر با 2πr است.
بنابراین چند نکته مهم است که باید به خاطر بسپارید.
dr خود نام یک متغیر است و به معنی d×r نیست. در واقع این متغیر بخش کوچکی از شعاع را در که مرحله کنونی قرار دارد نشان میدهد. نماد dr، dx یا هر چیز دیگر غالباً با یک فاصله از عبارت زیر انتگرال جدا میشود، برای مثال به صورت 2πr dr و این رابطه نیز ضرب تصور نمیشود.
همچنین باید بدانید که اگر r تنها متغیر مورد استفاده در انتگرال باشد، در این صورت فرض میگیریم که dr نیز زیر انتگرال وجود دارد. بدین ترتیب دقیقاً به همان معنی است. همچنین در صورتی که دو متغیر زیر انتگرال باشند، باید مشخص شود که در هر مرحله نسبت به کدام یک انتگرال میگیریم.
در نهایت باید به خاطر داشته باشید که r (شعاع) مانند رویکرد تایملپس تغییر مییابد و از 0 شروع شده و در نهایت به مقدار پایانی میرسد. زمانی که r را در چارچوب یک مرحله بنگریم بدین معنی خواهد بود که «اندازه شعاع در مرحله کنونی r است»، پس دقت کنید که در این مرحله r به معنی شعاع نهایی نیست.
این مباحث تا حدودی سردرگمکننده هستند. بنابراین در ادامه سعی میکنیم آنها را با هم تمرین کرده و بهتر درک کنیم.
تمرین کردن اصطلاحها
اگر بخواهیم مانند افراد خبره در مورد حسابان صحبت بکنیم، راهبرد اشعه ایکس خود را به صورت زیر میتوانیم توصیف کنیم:
| مفهوم شهودی | توصیف رسمی | نماد |
|---|---|---|
 | مشتقگیری از مساحت دایره با توجه به شعاع | مساحت d/dr |
 | مشتقگیری از مساحت دایره با توجه به محیط | مساحت d/dp |
 | مشتقگیری از مساحت دایره با توجه به محور x | مساحت d/dx |
به خاطر داشته باشید که مشتق صرفاً یک شکل را به مراحلی مانند حلقههایی با اندازه 2πr dr تقسیم میکند که اندازهگیری را آسانتر میکند. اگر یک حجمی که با لِگو ساختهایم را به آجرهای لگو تقسیم کنیم، صرفاً لگوهایی خواهیم داشت که روی زمین پخش شدهاند. اینک ما به انتگرال نیاز داریم تا قطعات لگو را در کنار هم قرار داده و اندازه حجم جدید را به ما اعلام کند. بنابراین دو اصطلاح مشتق و انتگرال با یکدیگر همکاری میکنند.
- مشتق میگوید: من شکل را برای تو تقسیم میکنم تا به صورت تکههایی با ارتفاع 2πr و عرض dr درآید.
- انتگرال میگوید: من تکههای مختلف را کنار هم به مانند یک مثلث قرار میدهم تا بتوانم آن را اندازهگیری کنم. مساحت کلی مثلث (قاعده × ارتفاع تقسیم بر 2) خواهد بود که در این مورد برابر با πr2 است.
در ادامه انتگرالهایی که برای اندازهگیری مراحل شکلهای مختلف موردنیاز است ارائه کردهایم:
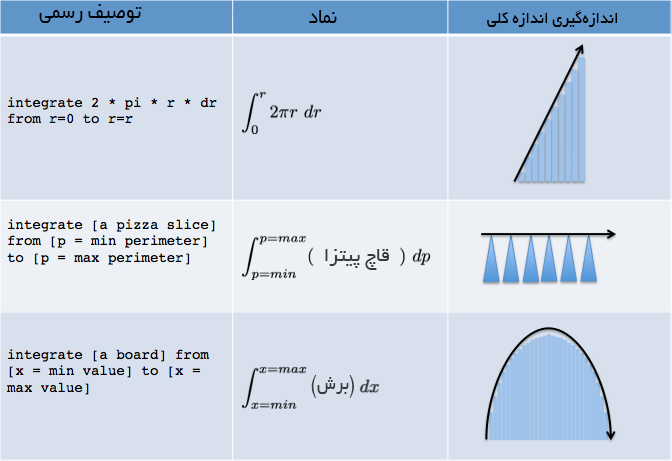
چند نکته لازم است در مورد مفاهیم مشتق و انتگرال بیان کنیم.
ما در اغلب موارد عبارت زیر انتگرال را به صورت یک «قاچ پیتزا» یا «برش» نامعین با استفاده از یک نام رسمی مانند (s(P یا (b(x بیان میکنیم. بنابراین باید ابتدا انتگرال را تنظیم کنیم و سپس در مورد فرمول دقیق برش یا قاچ نگران باشیم.
از آنجا که هر انتگرال نماینده قاچهایی از دایره اصلی ما است، میدانیم که یکسان خواهند بود. همچنین میدانیم که چسباندن مجموعهای از برشها از یک شکل، همواره شکل نهایی را به دست میدهد.
انتگرال غالباً به صورت «مساحت زیر منحنی» توصیف میشود. گرچه این تعریف صحیح است؛ اما همه واقعیت را بیان نمیکند. درست است که ما برشهای مستطیل زیر منحنی را به هم میچسبانیم؛ اما این نکته باعث میشود رویکرد اشعه ایکس و تایملپس را کاملاً نادیده بگیریم. چرا ما کلاً میخواهیم با یک مجموعه از برشها در برابر یک منحنی سر و کار داشته آبشیم. در اغلب موارد دلیل آن است که اندازهگیری آن برشها بسیار سادهتر از خود شکل است.
برای مطالعه بخش بعدی این مطلب روی لینک زیر کلیک کنید:
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- آموزش مشتق گیری و انتگرال گیری عددی در محاسبات عددی
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- آموزش جامع حساب دیفرانسیل و انتگرال پیش دانشگاهی
- انتگرال — به زبان ساده
- انتگرال و روش های محاسبه — به زبان ساده
- انتگرال توابع مثلثاتی — از صفر تا صد
==












