جریان متناوب (Alternating Current) – از صفر تا صد
پیشتر در مطلب القای فارادی یاد گرفتیم که چگونه میدان مغناطیسی متغیر با زمان میتواند نیروی محرکه القایی ایجاد کند. با توجه به این قانون میتوان با دوران یک سیمپیچ در میدان مغناطیسی، نیروی محرکه القایی ایجاد کرده و از آن استفاده کرد. بدلیل متفاوت بودن اندازه نیروی محرکه ایجاد شده در هر لحظه، به جریان الکتریکی ایجاد شده «جریان متناوب» (Alternating Current) گفته میشود. در این قسمت قصد داریم تا در مورد این نوع از جریانها و روابط حاکم بر آنها صحبت کنیم.


منبع AC
با توجه به متغیر بودن جریان و ولتاژ متناوب، از نماد زیر جهت نشان دادن منبع متناوب جریان الکتریکی استفاده میشود.

رابطه زیر بیان کننده نمونهای از ولتاژ متناوب الکتریکی است.
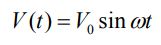
در رابطه بالا V0 تحت عنوان دامنه شناخته میشود. همچنین این رابطه نشان میدهد که ولتاژ الکتریکی بین V۰ ± تغییر میکند. نمودار زیر تغییرات زمانی ولتاژ را نشان میدهد.

از ریاضیات مفهوم تابع دورهای را میشناسیم. در حقیقت به تابع یا کمیتی که در زمان تکرار میشود، تابع یا کمیت دورهای (Periodic) گفته میشود. برای چنین توابعی اعداد ثابتی همچون دوره (T) و فرکانس (f) تعریف میشود. برای ولتاژ، مقدار فرکانس برابر با f=1/T و ω = 2π f نشان دهنده فرکانس زاویهای است.واحد فرکانس، هرتز و واحد دوره، ثانیه است.
زمانی که یک منبع ولتاژ به مداری RLC متصل شده باشد، انرژی دائمی تولید شده توسط منبع، منجر به جبران انرژی تلف شده در مقاومت میشود. نوسانات بار، جریان و اختلاف پتانسیل، تحت عنوان نوسانات اجباری شناخته میشوند.
پس از سپری شدن زمان گذار اولیه، جریانی متناوب (AC) که در نتیجه اختلاف پتانسیل نوسانی است، در مدار جریان میشود. جریان مذکور مطابق با رابطه زیر، با زمان تغییر میکند.
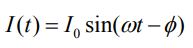
طبق رابطه بالا دامنه و فرکانس ولتاژ بهترتیب برابر با I0 و Φ است.
مدار جریان متناوب
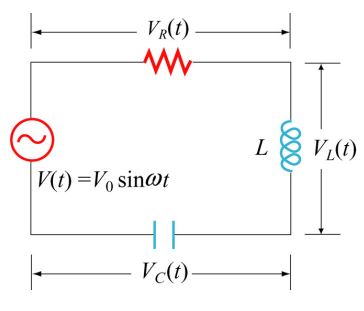
قبل از بررسی مدار RLC در ابتدا اجازه دهید تا حالتی ساده را بررسی کنیم که در آن مداری مطابق با شکل زیر به منبعی متناوب متصل شده است. با اعمال قانون کیر-شهف برای مدار پایین، داریم:
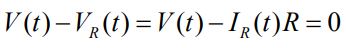
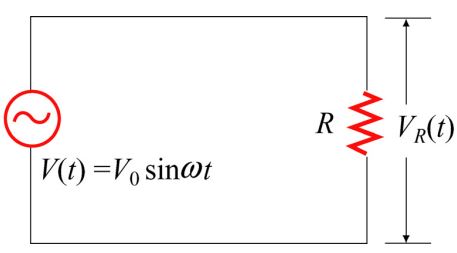
در این رابطه VR(t) = IR(t) R، افت ولتاژ لحظهای در مقاومت در نظر گرفته میشود. همچنین جریان لحظهای در مقاومت برابر است با:
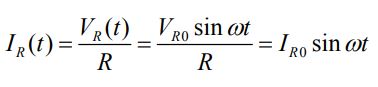
در این رابطه VR0 = V0 و IR0 = VR0/R بهترتیب جریان و ولتاژ ماکزیمم را در مقاومت الکتریکی نشان میدهند. با مقایسه رابطه با رابطه بالا، اندازه φ برابر با صفر بدست میآید. این مقدار نشان دهنده همفاز بودن ولتاژ و جریان الکتریکی است. در حقیقت این دو کمیت در یک زمان به مقدار ماکزیمم خود و در یک زمان به مینیممشان میرسند.
نمودار زیر وابستگی زمانی جریان و ولتاژ الکتریکی را در مقاومت نشان میدهد.
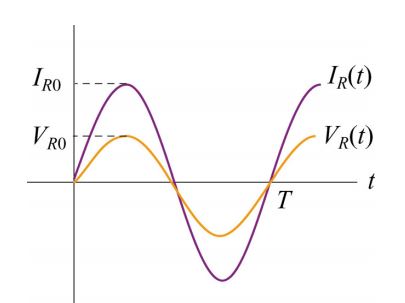
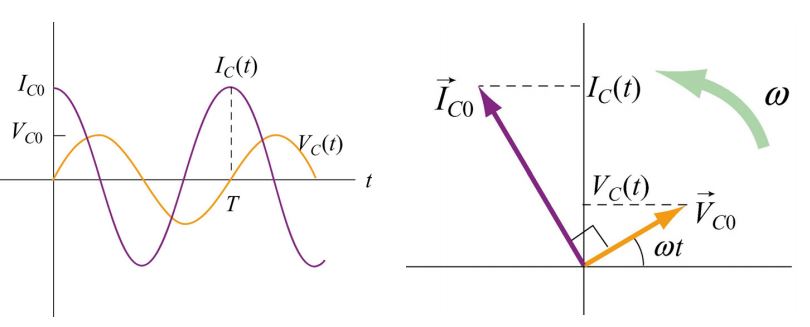
رفتار (IR(t و (VR(t را میتوان با استفاده از نمودار فازیِ شکل زیر نمایش داد.

«فازور» (Phasor)، برداری دورانی است که ویژگیهای زیر را دارد.
- طول فازور متناسب با دامنه کمیت است.
- بردار بهصورت پادساعتگرد با سرعت زاویهای ω دوران میکند.
- تصویر بردار فازور روی محور y، نشان دهنده اندازه کمیتها است.
با توجه به اینکه فازور مفهومی برداری است، در نتیجه بایستی با استفاده از بردار آن را نمایش داد. اندازه فازور برابر با مقدار ثابت V R0 است. اندازه این بردار در راستای محور عمودی برابر با VR0= sin ωt است. این مقدار نشان دهنده (VR(t و برابر با افت پتانسیل در مقاومت الکتریکی، در زمان t است. همین مفهوم را میتوان برای جریان الکتریکی عبوری از مقاومت نیز تعریف کرد.
با استفاده از فازور نشان داده شده در شکل ۲ میتوان دید که جریان و پتانسیل الکتریکی در هر لحظه همجهت هستند. مقدار میانگین جریان الکتریکی در یک دوره با <I> نمایش داده میشود. این عدد ثابت برابر است با:
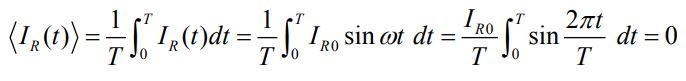
دلیل صفر شدن عبارت بالا، صفر شدن میانگین < sin ωt > است. با توجه به دورهای بودن کمیتهای مربوط به جریان متناوب، روابط زیر جهت میانگینگیری پرکاربرد هستند.

با توجه به روابط بالا، میتوان دید که مقدار میانگین توان دوم جریان، غیرصفر است. این مقدار در رابطه زیر محاسبه شده است.
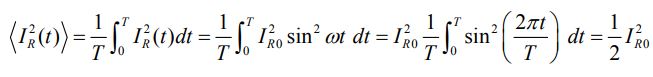
عددی تحت عنوان «مقدار موثر» (rms) میتواند مفید باشد. این مقدار برابر است با:
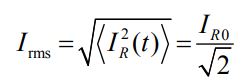
به طریقی مشابه ولتاژِ rms بهشکل زیر بدست میآید.

برای نمونه ولتاژ rms و فرکانس برق خانگی بهترتیب برابر باو f=60 Hz هستند. از این رو توان تلف شده در مقاومت برابر است با:
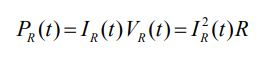
با جایگذاری روابط جریان و ولتاژ الکتریکی در رابطه بالا و میانگیری از آن، توان میانگین مطابق با رابطه زیر محاسبه میشود.
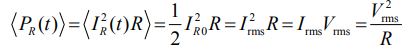
مدار خالص القایی
مداری شامل یک منبع AC و القاگر را مطابق با شکل زیر در نظر بگیرید.
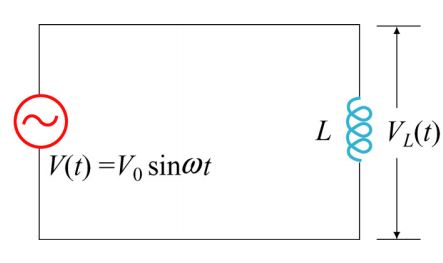
با توجه به مفاهیم بیان شده در مطلب مدار RLC، مدار بالا معادل با اتصال القاگر به خازنی با ظرفیت بینهایت است. با اعمال قانون کیر-شهف اصلاح شده برای مدار مفروض، داریم:
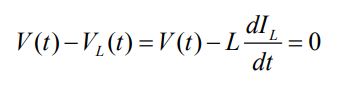
رابطه بالا را میتوان بصورت زیر بازنویسی کرد:
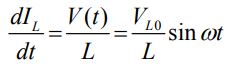
در رابطه بالا V0L برابر با V0 است. با انتگرالگیری از رابطه بالا داریم:
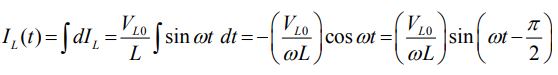
در بدست آوردن رابطه بالا، از قانون زیر استفاده شده است.
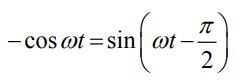
همچنین با مقایسه رابطه بالا و (I(t) = I0 sin (ωt-φ، دامنه جریان در القاگر برابر با رابطه زیر بدست میآید.
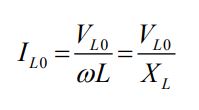
در رابطه بالا XL = ωL است و آن را تحت عنوان «راکتانس القایی» (Inductive Reactance) میشناسند. این کمیت از جنس مقاومت الکتریکی است؛ از این رو واحد SI آن برابر با اهم (Ω) در نظر گرفته میشود.
تفاوت XL با مقاومت این است که راکتانس القایی بهصورت خطی با فرکانس زاویهای ω تغییر میکند. بهطور دقیقتر راکتانس القایی بهصورت خطی با فرکانس زاویهای افزایش مییابد. این تغییر در نتیجه این واقعیت است که در فرکانسهای بالاتر، جریان الکتریکی با زمان افزایش مییابد. به بیانی دیگر، راکتانس القایی با نزدیک شدن ω به صفر، به همین مقدار نزدیک میشود. با مقایسه روابط بالا با یکدیگر مقدار φ برابر با π/۲+ بدست میآید.
نمودار ولتاژ، جریان و فازور مرتبط با آنها در دو نمودار زیر نشان داده شده است.
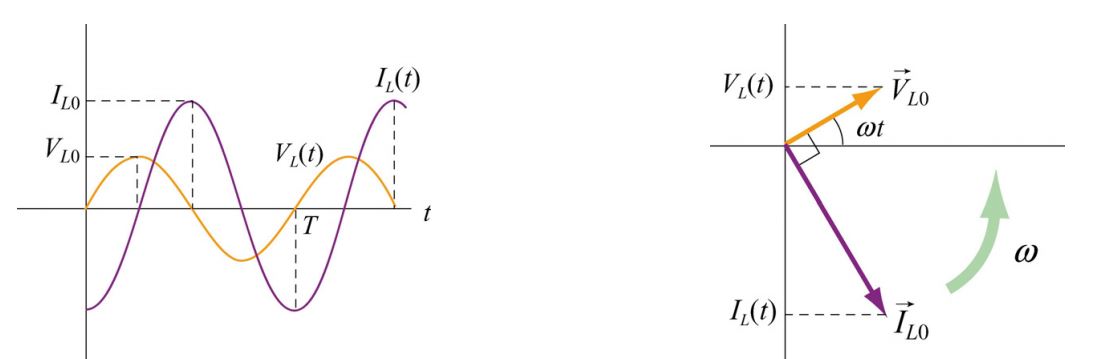
همانطور که در نمودارهای بالا نیز میبینید، جریان (IL(t و (VL(t به اندازه π/۲+ با یکدیگر فاصله دارند. برای نمونه پس از ماکزیمم شدن ولتاژ، به اندازه ۱/۴ زمان سیکل طول میکشد تا جریان به مقدار ماکزیمم خود برسد.
مدار خالص خازنی
مدار خالص خازنی به مداری مطابق با شکل زیر اشاره دارد که در آن از القاگر و مقاومت الکتریکی استفاده نشده باشد.
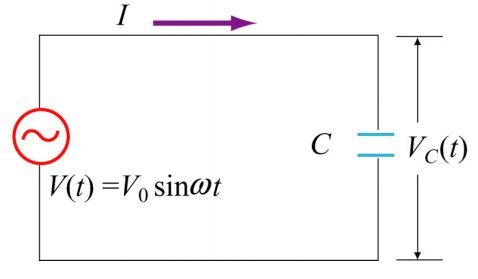
قانون کیر-شهف در این حالت برابر است با:
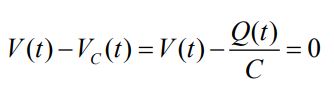
این رابطه را میتوان بر حسب بار الکتریکی، به شکل زیر بیان کرد:
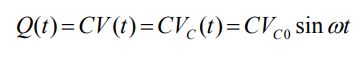
در این رابطه نیز VC0 برابر با V0 است. با استفاده از تعریف جریان الکتریکی داریم:
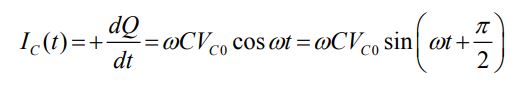
در بدست آوردن رابطه بالا نیز از قانون مثلثاتی (Cos ωt = sin (ωt + π/2 استفاده شده. رابطه بالا، مقدار ماکزیمم جریان الکتریکی را برابر با مقدار زیر بدست میدهد.
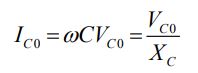
در این رابطه، مقدار ثابت Xc برابر با عبارت زیر است.
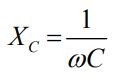
عبارت بالا با عنوان «راکتانس خازنی» (Capacitance Reactance) شناخته میشود. واحد SI این کمیت برابر با اهم و اندازه آن، نشان دهنده مقاومت موثر مدار خالص خازنی است. توجه داشته باشید که XC بهطور معکوس با C و ω رابطه دارد و مقدار این کمیت برابر با کم شدن فرکانس واگرا میشود. با مقایسه روابط بالا با هم، اختلاف فاز برابر با مقدار زیر بدست میآید.
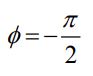
در در نمودار زیر، ولتاژ، جریان و نمودار فازوری جریان الکتریکی نشان داده شده است.
توجه داشته باشید که در زمان t=0، ولتاژ دو سر خازن برابر با صفر و جریان الکتریکی مدار، بیشینه است. بنابراین جریان الکتریکی به اندازه ۱/۴ زمان کل سیکل، زودتر به مقدار ماکزیمم خود میرسد.
مدار سری RLC
مطابق با شکل زیر، مداری شامل مقاومت، القاگر، خازن و منبع الکتریکی را در نظر بگیرید. با اعمال قانون کیر-شهف برای نمودار زیر، میتوان نوشت:
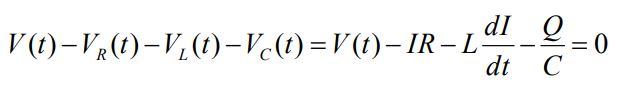
رابطه بالا ما را به معادله دیفرانسیل زیر میرساند.
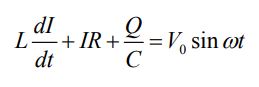
فرض کنید که در حالت اولیه، خازن باردار نیست؛ بنابراین جریانِ I=dQ/dt متناسب با افزایش بارهای الکتریکی در خازن است. از این رو معادله بالا را میتوان بهصورت زیر بازنویسی کرد.
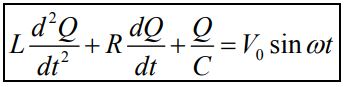
یکی از جوابهای ممکن برای رابطه بالا برابر است با:
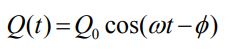
در این رابطه دامنه و فاز بهترتیب برابر با مقادیر زیر هستند.
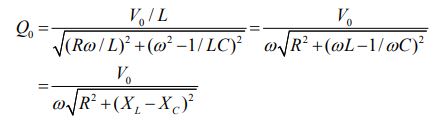
همچنین اختلاف فاز φ برابر است با:
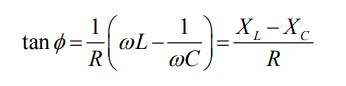
رابطه کلی مربوط به جریان I را بهشکل زیر فرض میکنیم.
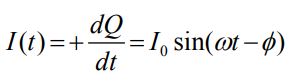
دامنه رابطه فوق برابر با مقدار زیر است:
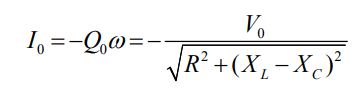
توجه داشته باشید که دامنه و اختلاف فاز در تمامی نقاط مدار با یکدیگر برابر هستند. در تصاویر زیر، نمودارهای ولتاژ، جریان و فازوری آنها نشان داده شده است.
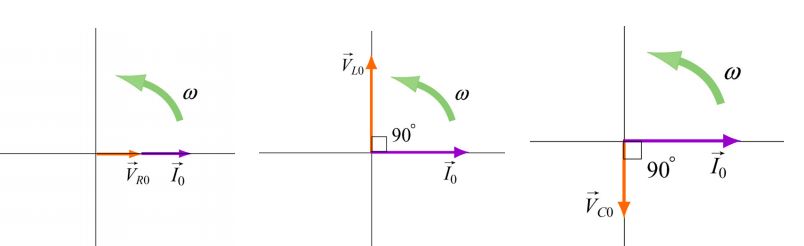
با توجه به تصاویر بالا، ولتاژ لحظهای هر کدام از اجزاء مدار در سه رابطه زیر نشان داده شدهاند.
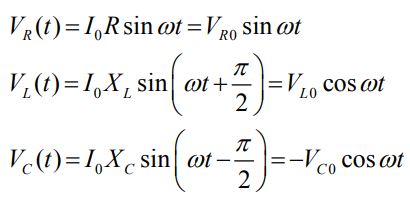
ثوابت روابط فوق برابر با مقادیر زیر هستند.
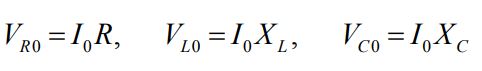
مقادیر بالا، دامنه اختلاف پتانسیل در المانهای مدار RLC را نشان میدهند. با استفاده از نمودار فازوری، روابط برداری بین ولتاژها را میتوان به شکل زیر بیان کرد:
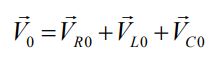
نکته جالب در مورد اختلاف فاز این است که در مدار RLC نیز جریان الکتریکی به اندازه π/۲ از ولتاژِ خازن جلوتر و به همین میزان از ولتاژِ القاگر عقبتر است. شکلهای زیر، نمودار ولتاژ فازوری و برآیند آنها را نشان میدهند.
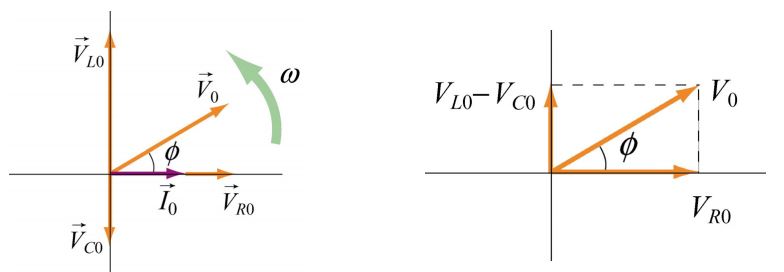
با استفاده از نمودار سمت چپ تصویر بالا، اندازه برآیند ولتاژها برابرند با:
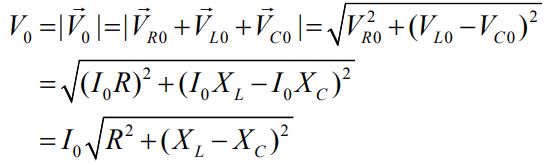
نکته بسیار مهم در مورد بررسی جریان متناوب در مدار RLC این است که نمیتوان با جمع جبری مقادیر ولتاژ ماکزیمم اجزاء مدار، مقدار ماکزیمم را بدست آورد.
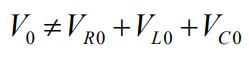
دلیل ارائه نامساوی بالا این است که ولتاژ اجزا مدار در یک زمان ماکزیمم یا مینیمم نمیشوند و در زمانهای متفاوتی به بیشینه خود میرسند.
امپدانس (Impedance)
در بالا گفتیم که راکتانس القایی XL = ωL و راکتانس خازنی XC = 1/ωL نقش مقاومت موثر را در مدارات خالص القایی و خازنی بازی میکنند. حال این سوال مطرح میشود که در مدار RLC که هر سه جزء مقاومت، خازن و القاگر وجود دارند، مقاومت موثر به چه شکل تعریف میشود؟
در مدار RLC، مقاومت موثر در مفهومی تحت عنوان امپدانس معرفی میشود. امپدانس در یک مدار RLC، با استفاده از رابطه زیر بدست میآید.
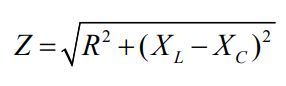
شکل برداری Z ،XL ،XC در زیر نشان داده شده است.
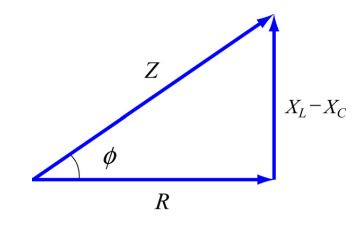
واحد امپدانس نیز همچون راکتانس خازنی و القایی برابر با اهم هستند. جریان الکتریکی I، بر حسب Z، به شکل زیر قابل بیان است:
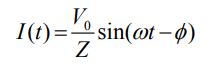
رابطه مربوط به Z نشان میدهد که این مقدار نیز همچون راکتانس وابسته به فرکانس زاویهای ω است.
تشدید
رابطه نشان میدهد که دامنه جریانِ I0=V0/Z، زمانی ماکزیمم است که اندازه Z به مقدار مینیمم خود برسد. زمانی این اتفاق رخ خواهد داد که XL=XC باشد یا معادل با آن رابطه ωL=1/ωC بین فرکانسها برقرار باشد. در نتیجه:
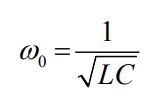
به فرآیندی که در آن جریان I0 ماکزیمم شود، فرآیند تشدید و به فرکانسی که این اتفاق در آن رخ دهد، فرکانس تشدید گفته میشود. در حالت تشدید، Z=R و دامنه و اختلاف فازِ جریان بهترتیب برابر با مقادیر زیر هستند.
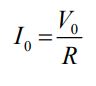
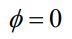
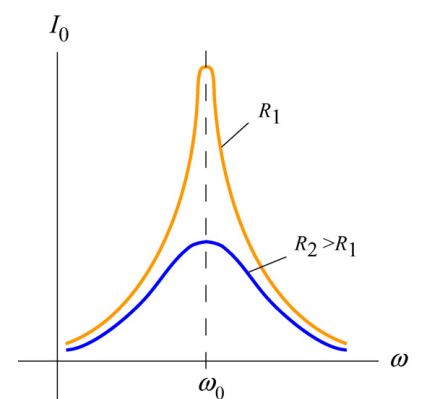
در حالت تشدید، جریان الکتریکی در ماکزیمم مقدار خود قرار دارد. نمودار زیر نشان دهنده تغییرات دامنه جریان بر حسب فرکانس زاویهای است.
توان در مدارهای AC
در مدار سریِ RLC، توان تحویل داده شده به مدار در هر لحظه برابر است با:
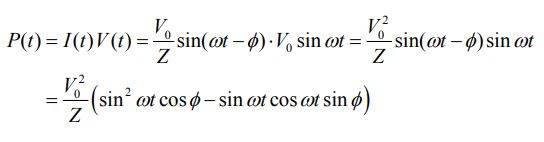
با استفاده از رابطه sin (ωt - φ) = sin ωt cos φ - cos ωt sin φ میانگین توان تحویل داده شده به مدار در یک سیکل برابر است با:
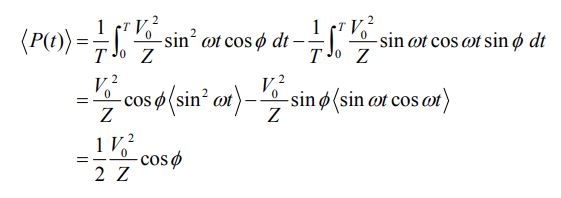
البته عبارت بالا را میتوان بر حسب RMS، به شکل زیر بیان کرد:
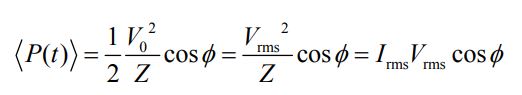
عدد Cos φ تحت عنوان ضریب توان شناخته شده و مقدار آن برابر است با:
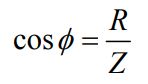
از این رو مقدار میانگین توان <(P(t> برابر است با:
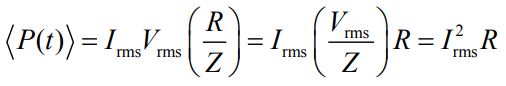
در نمودار زیر میزان توان تحویل داده شده به مدار در فرکانسهای زاویهای مختلف نشان داده شده است.
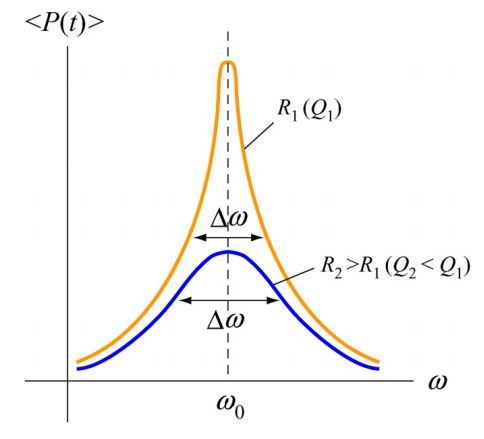
نمودار بالا نشان میدهد که در حالت تشدید (ω=ω0)، توان تحویل داده شده به مدار، در ماکزیمم مقدار خود قرار دارد. در این حالت Cos φ =1 است و مقادیر R و Z با یکدیگر برابر هستند (Z=R).
در حالت تشدید، ماکزیمم توان تحویلی به مدار برابر است با:
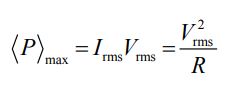
عرض قله
همانطور که در بالا نشان داده شد، توان تحویلی به مدار از صفر شروع شده، به مقداری ماکزیمم رسیده و سپس افت میکند. معمولا فرکانسهایی که در آن توان از نصف مقدار ماکزیممش بیشتر باشد، در یک دسته قرار میگیرند. با توجه به شکل زیر بین دو فرکانسِ +ω و -ω، توان تحویل داده شده به مدار، بیشتر از نصف توان ماکزیمم است. فرض کنید باشد. به این فاصله عرض قله گفته میشود. جهت بدست آوردن Δω، در ابتدا رابطه مربوط به مقدار میانگین توان را بهشکل زیر بنویسید.
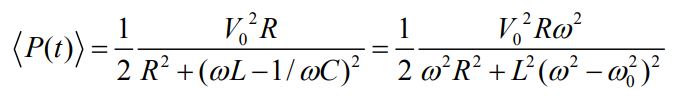
از آنجایی که است، در +ω و -ω، مقدار توانِ ماکزیمم نصف خواهد بود. از این رو جهت بدست آوردن فرکانسهای مذکور میتوان نوشت:
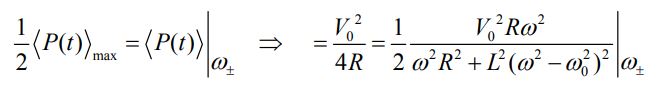
با توجه به عبارت فوق، رابطه مربوط به فرکانسهای مد نظر برابر است با:
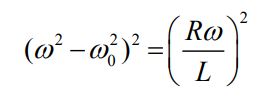
رابطه بالا دو حالت را پیش خواهد آورد.
حالت اول
در حالت اول پاسخ جذر بالا را مثبت فرض میکنیم. در این حالت داریم:
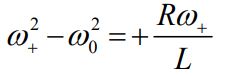
با حل رابطه بالا، حد بالای عرض فرکانس برابر با مقدار زیر بدست میآید.
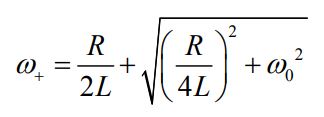
حالت دوم
با محاسبه جذر مفروض و فرض کردن علامت منفی برای آن، -ω برابر با مقدار زیر بدست میآید.
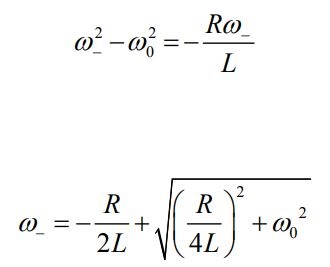
با بدست آمدن حد بالا و پایین فرکانس، عرض آن برابر با مقدار زیر بدست میآید.
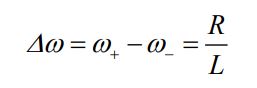
زمانی که ω∆ معلوم باشد، عددی ثابت تحت عنوان ضریب کیفیتِ Q را میتوان مطابق با رابطه زیر تعریف کرد. این عدد برابر است با:
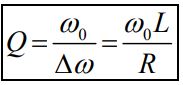
ترانسفورماتور
ترانسفورماتور دستگاهی است که با استفاده از آن میتوان جریان AC یا DC را افزایش یا کاهش داد. مطابق با شکل زیر نوع معمول این دستگاه از هستهای آهنی ساخته شده که سیمی فلزی دور آن پیچیده شده است. سیمپیچ اولیه از N1 حلقه تشکیل و به منبع متغیر (V1(t متصل شده. این در حالی است که سیمپیچ دوم دارای N2 حلقه و متصل به بار مقاومتی R2 است.
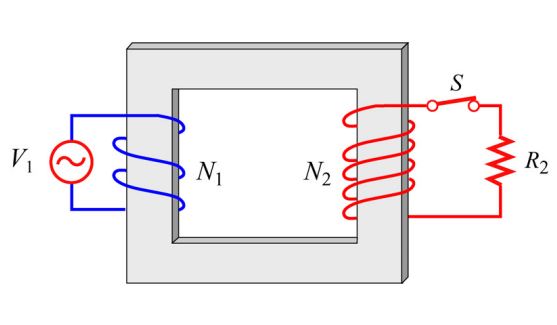
عملکرد ترانسفورماتور بر این مبنا است که اگر دو سیمپیچ در کنار یکدیگر قرار گرفته باشند و در یکی از آنها جریانی متناوب وجود داشته باشد، در دیگری نیز جریانی متناوب القا خواهد شد.
برای سیمپیچ شماره ۱، با فرض مقاومت ناچیز سیمپیچ، قانون القاء فارادی را میتوان به شکل زیر بیان کرد:
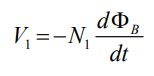
در رابطه فوق ΦB برابر با شار مغناطیسی عبوری از یک حلقه از سیمپیچ شماره ۱ است. معمولا از هستههای آهنی، جهت ارتباط میان سیمپیچ اول و دوم استفاده میشود. دلیل این استفاده این است که تمامی شار عبوری توسط سیمپیچ شماره ۱ از سیم پیچ دوم عبور کند.
از طرفی ولتاژ القا شده در سیمپیچ دوم نیز برابر است با:
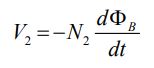
در حالتی که با ترانسفورماتوری ایدهآل مواجه هستیم، تلفات توان ناشی از اثر ژول را میتوان در نظر نگرفت؛ بنابراین تمامی توان متصل شده به سیمپیچ اول به سیمپیچ دوم انتقال خواهد یافت. یا به بیانی دیگر:
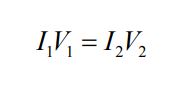
اگر فرض کنیم که هیچ مقداری از شار مغناطیسی تولید شده توسط سیمپیچ شماره ۱ از هسته نشت نشود و تمامی آن به سیمپیچ شماره ۲ منتقل شود، با ترکیب دو روابط بالا داریم:
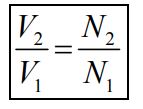
همچنین با ترکیب دو رابطه بالا، رابطه بین تعداد دورهای سیمپیچ و جریان آنها نیز بهشکل زیر بدست میآید.
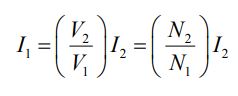
روابط بالا نشان میدهد که با افزایش تعداد دور میتوان ولتاژ خروجی را افزایش و با کاهش آن ولتاژ را کاهش داد.
مدار موازی RLC
در گذشته در مورد مدار RLC بحث شد. در این قسمت قصد داریم تا در مورد مواردی صحبت کنیم که در آن مطابق با شکل زیر از سه جز خازن، مقاومت و القاگر بهصورت موازی استفاده شده است.

در مدار بالا ولتاژ الکتریکی با رابطه (V (t) = V0 sin (ωt تغییر میکند. بر خلاف مدار سری RLC، در این حالت اختلاف ولتاژ لحظهای دو سر هر جزء با یکدیگر برابر است. همچنین در مقاومت، ولتاژ و جریان الکتریکی با یکدیگر همفاز هستند. البته دقت داشته باشید که در این حالت جریان در هرکدام از اجزا متفاوت است.
جهت بررسی این مدار، در ابتدا جریان الکتریکی موجود در مقاومت را برابر با رابطه زیر فرض میکنیم.
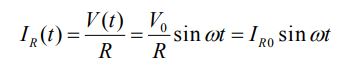
با داشتن ولتاژ دو سر القاگر، میتوان رابطه زیر را جهت بدست آوردن جریان آن بدست آورد.
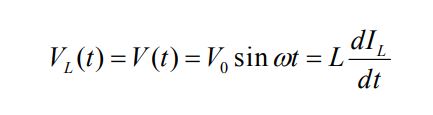
با انتگرالگیری از رابطه بالا داریم:
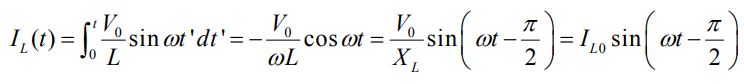
در رابطه بالا مقادیر LL0=V0/XL و XL=ωL، برابر با راکتانس القایی هستند. به طور مشابه با نوشتن ولتاژ دو سر خازن داریم:
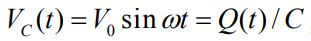
با مشتق گیری از رابطه فوق، جریان الکتریکی، برابر با رابطه زیر بدست میآید.
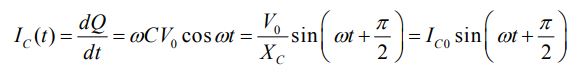
در رابطه بالا ثوابت XC=1/ωC و IC0=V0 راکتانس خازنی هستند. با بکارگیری قانون گره، رابطه جریانها در شاخهها را میتوان بهصورت زیر بیان کرد:
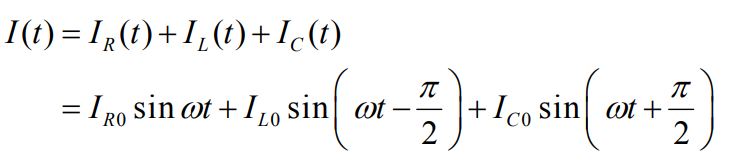
جریانهای ارائه شده در بالا را میتوان با استفاده از نمودار فازوری ارائه شده در زیر توصیف کرد.
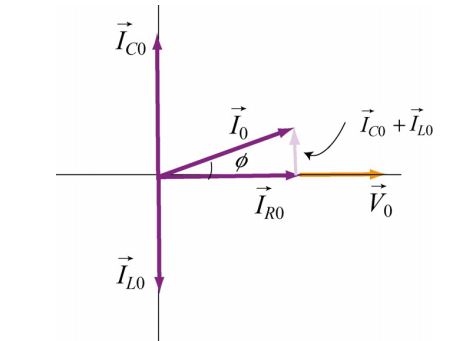
با استفاده از نمودار فازوری ارائه شده در بالا داریم:
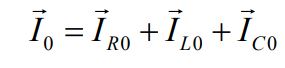
با توجه به رابطه بالا، ماکزیمم میزان جریان (I0)، به شکل زیر قابل محاسبه کرد.
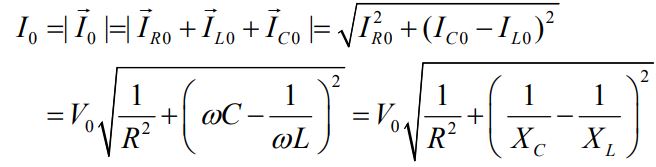
همانند حالت سری، در این حالت نیز نمیتوان با استفاده از جمع جبری مقادیر جریان، جریان ماکزیمم را یافت. با استفاده از رابطه بالا و رابطه I0=V0/Z، امپدانس معکوس مدار برابر با رابطه زیر بدست میآید.
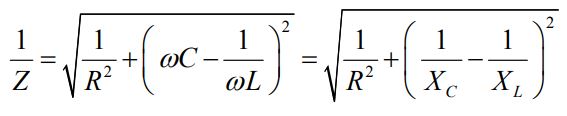
رابطه بین امپدانس، مقاومت و راکتانس در شکل زیر نشان داده شده است.
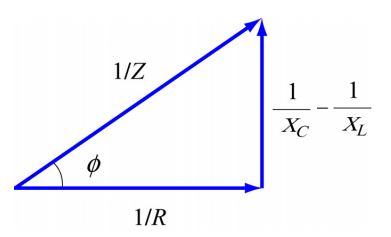
با استفاده از نمودار فازوری شکل ۳، اختلاف فاز را میتوان مطابق با رابطه زیر بدست آورد.
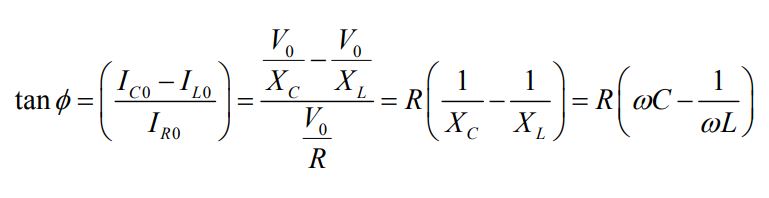
شرایط تشدید برای مدار موازی RLC، نتیجه زیر را میدهد.
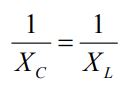
در نتیجه فرکانس تشدید برابر است با:
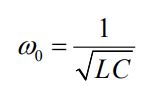
نتیجه بالا از این نظر برجسته است که اندازه فرکانس تشدید برابر با حالت سری است. در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی برق، آموزشهای زیر نیز به شما پیشنهاد میشوند:













با سلام و احترام
می خواستم بپرسم فرمول w=1/RC از کجا بذست می آید؟
(در آموزش فیلترهای پایین گذر به آن اشاره داشتید)
با تشکر و سپاس
اگه برای مبحث سه فازم ویدئو درست کنین خیلی خوبه. تشکر
آقا دمتون گرم خیلی عالی بود. من رشتم چیز دیگه ایه به این مبحث برخوردم باید یاد میگرفتم 1.5 ساعته فول شدم. خدا امواتتو بیامرزه.
سلام
چرا خازن در فرکانس های پایین جریان را از خور عبور نمیدهد
ممنون از مطالبتون
با سلام و تشکر از همراهی شما با مجله فرادرس
راکتانس یک خازن که ماهیتی شبیه به مقاومت دارد با رابطه زیر به دست میآید:
Xc=1/ωC=1/2πfC
اگر در رابطه فوق به جای f مقادیر کوچک فرکانس (نزدیک به صفر) قرار دهیم،آنگاه به مقدار بینهایت میرسیم که نشان دهنده عدم هدایت خازن در فرکانسهای بالا است که میتوان آن را مدار باز نشان داد.