کنترل فازی – از صفر تا صد
در آموزشهای قبلی مجله فرادرس، با برخی از رویکردهای طراحی سیستمهای کنترل از قبیل کنترل پیشبین مدل آشنا شدیم. در این آموزش، با یک روش کنترلی دیگر، به نام کنترل فازی آشنا میشویم.
امروزه کاربرد مجموعههای فازی در کنترل خودکار توجه زیادی را به خود جلب کرده است. در سال ۱۹۷۴، اولین کاربرد موفق منطق فازی در مهندسی کنترل، در یک فرایند آزمایشگاهی گزارش شد. کنترل کوره پخت سیمان یکی از اولین موارد کاربرد صنعنتی کنترل فازی بود. پس از ارائه اولین محصول تجاری در سال ۱۹۸۷ به بازار، که در تولید آن از منطق فازی استفاده شده بود، کاربرد کنترل فازی (Fuzzy Control) افزایش قابل توجهی یافت. امروزه تعدادی از محیطهای طراحی به کمک رایانه (CAD) برای طراحی فازی با سختافزار VLSI جهت اجرای سریع ادغام شدهاند. تاکنون، کنترل فازی به سیستمهای مختلفی از قبیل لوازم برقی، قطارها، ترافیک و... اعمال شده است.
کنترلکننده منطق فازی، یک پروتکل کنترلی را با قواعد «اگر-آنگاه» توصیف میکند؛ مثلاً «اگر دما پایین باشد، کمی شیر گرمایش را باز کن.» ابهام (عدم قطعیت) در تعریف عبارات زبانی (مثلاً دمای پایین)، با استفاده از مجموعههای فازی، که مجموعههایی با مرزهای دارای همپوشانی هستند، نمایش داده میشود (شکل ۱).

در چارچوب مجموعه فازی، یک عنصر خاص در دامنه میتواند همزمان به چند مجموعه متعلق باشد (با درجات عضویت متفاوت ). برای مثال، به مجموعه دماهای بالا با عضویت و مجموعه دماهای متوسط با عضویت تعلق دارد. این انتقال تدریجی از عضویت به عدم عضویت، به تولید یک خروجی استدلالی هموار با قواعد اگر-آنگاه فازی کمک میکند.
تاریخچه کنترل فازی
کنترل فازی از یک رساله دکتری در زمینه هوش مصنوعی متولد شد. این رساله بین سالهای ۱۹۷۲ تا ۱۹۷۴ به انجام رسید. هدف پژوهش، این بود که کامپیوترها با مشاهده کار یک انسان، یاد بگیرند آن را انجام دهند. آزمایشی که برای پژوهش مورد نظر انتخاب شد، کنترل یک نمونه موتور بخار بود. ورودیهای کنترل در دسترس این سیستم، دو مورد بودند: «گرما» که فشار بخار در یک بویلر را تولید میکرد و «دریچه گاز» که بخار را به تک سیلندر موتور تزریق میکرد و روی سرعت آن تأثیر میگذاشت. هدف کنترل، ثابت نگه داشتن فشار بویلر و سرعت موتور بود. برای اینکه درک بهتری از چگونگی گسترش کنترل فازی از این پروژه پژوهشی داشته باشیم، باید با چند موضوع کلیدی آن آشنا شویم. در ادامه، این موارد را بیان میکنیم.
محیط محاسباتی
یک کامپیوتر هیبریدی تقریباً مانند مینیکامپیوتر PDP-8S با کلمات 8K (کلماتی ۱۲ بیتی) با رم هسته مغناطیسی برای انجام محاسبات ساخته شد. نوار کاغذی اصلیترین بستر برای ذخیره و پشتیبانی اطلاعات بود. در آن زمان، ماوس هنوز اختراع نشده بود و ارتباط از طریق تلهتایپ انجام میشد. ورودیها و خروجیهای موتور بخار با این کامپیوتر هیبریدی تنظیم و خوانده میشدند. اجرای یک بار آزمایش، مستلزم این بود که تلهتایپ سرعت و فشار فعلی را چاپ کرده و منتظر بماند تا اپراتور با تایپ تنظیمات مقادیر گرما و دریچه گاز پاسخ دهد. با فشار دادن کلید بازگشت، کامپیوتر این تنظیمات را حمل کرده و با تایپ قرائتهای جدید سرعت و فشار پاسخ میداد. این عملیات تا جایی ادامه پیدا میکرد که دیگ از آب خالی شده و آماده شروع یک اجرای دیگر قابل انجام میشد.
چارچوب نظری پژوهش
این مطالعه عاری از هرگونه فرمولبندی خاص ریاضی بود. با توجه به منابع محدود محیط محاسباتی، سادهترین کار، شروع با استفاده از رویکرد یادگیری بیزی بود. ایده کار بهروزرسانی احتمالات کنش اعمالی به موتور بخار بود. واضح است که این روش ساده بوده و احتمال میرفت همگرایی احتمالاتِ یادگیری شده با شکست مواجه شود. دلیل این شکست هم مشخص بود؛ اپراتور انسانی علاوه بر حالت فعلی، حالات گذشته سیستم را نیز در نظر میگرفت. الگوریتم باید به گونهای بازبینی میشد تا حالات قبلی را نیز شامل شود. اما این نگرانی وجود داشت که الگوریتم پیچیدهتر شود و به رم موجود آسیب بزند.
ورود نظریه مجموعه فازی
برای حفظ جایگاه پژوهش، یک رویکرد جایگزین مورد بررسی قرار گرفت. نظریه مجموعههای فازی، تقریباً از سال ۱۹۶۵ وجود داشت، اما در سال ۱۹۷۳، دکتر زاده مقالهای در مجله IEEE SMC منتشر کرد که به جای شرح نظریه با عبارات نظری مجموعههای سنتی، راهی برای تشکیل الگوریتمها بر اساس مجموعههای فازی ارائه داد. یک الگوریتم کنترل فازی به ماشین «میگوید» که چگونه موتور بخار را کنترل کند، به جای آنکه با مشاهده کنشهای اپراتور انسانی یاد بگیرد که چه کاری را انجام دهد. ممدانی اولین الگوریتم کنترل فازی را در ۴ روز ساخت و آن را به سهولت برای مدل موتور بخار بررسی کرد. این الگوریتم شامل تعدادی قوانین فازی بود؛ از جمله: «اگر خطای فشار بسیار مثبت است و تغییر خطای فشار متوسط منفی نیست، آنگاه گرما را به اندازه خیلی مثبت تغییر بده.» در این قانون، متغیرهای اندازهگیری و کنترل با حروف پررنگ (بولد) و مقادیر فازی آنها به صورت کج (ایتالیک) نمایش داده شدهاند.
دلایل استفاده از کنترل فازی
نظریه کنترل رایج از مدل ریاضی (تحلیلی) صریح یک فرایند تحت کنترل و مشخصات رفتار مطلوب حلقهبسته برای طراحی یک کنترلکننده استفاده میکند. اگر به دست آوردن مدل دشوار باشد یا (بخشی از آن) ناشناخته یا بسیار غیرخطی باشد، این رویکرد با مشکل مواجه خواهد شد. طراحی کنترلکننده برای کارهای روزمره به ظاهر ساده، مانند رانندگی یک خودرو یا محکم گرفتن یک جسم شکستنی، هنوز در رباتیک با چالش همراه است. این در حالی است که انسان این کارها را به آسانی انجام میدهد. تاکنون، بشر از مدلهای ریاضی یا مسیرهای دقیق برای کنترل چنین فرایندهایی استفاده نکرده است.
بسیاری از فرایندهای صنعتی که با اپراتورهای انسانی کنترل میشوند، نمیتوانند از روشهای کنترل رایج برای خودکار شدن بهره ببرند، زیرا عملکرد این کنترلکنندهها اغلب نسبت به اپراتورها مناسب نیست. یکی از دلایل این امر، آن است که کنترلکنندههای خطی که اغلب در کنترل سنتی مورد استفاده قرار میگیرند، برای سیستمهای غیرخطی مناسب نیستند. دلیل دیگر این است که انسان اطلاعات مختلفی را جمعآوری، و استراتژیهای کنترل را با یکدیگر ترکیب میکند که نمیتوان آنها را در یک قانون کنترل تحلیلیِ تنها تجمیع کرد.
اصل اساسی کنترل دانشبنیان (خبره)، ثبت و پیادهسازی تجربه و دانش موجود خبرهها (یعنی اپراتورهای فرایند) است. یک نوع خاص کنترل دانشبنیان کنترل قاعدهمحور فازی است که در آن، کنشهای کنترلی متناظر با شرایط خاص سیستماند و بر اساس قوانین اگر-آنگاه فازی توصیف شدهاند.
در این کنترلکنندهها، از مجموعههای فازی برای تعریف مفهوم مقادیر کیفی ورودیها و خروجیهای کنترلکننده استفاده میشود؛ مثلاً خطای «کوچک» و عمل یا کنش کنترلی «بزرگ». منطق فازی میتواند ماهیت پیوسته فرایندهای تصمیمگیری انسانی را ضبط کند و به همین ترتیب، بهبود قطعی نسبت به روشهای مبتنی بر منطق دودویی یا باینری (که به طور گسترده در کنترلکنندههای صنعتی مورد استفاده قرار میگیرند) دارد.
کار اولیه در کنترل فازی، با اهداف زیر انجام شد:
- تقلید از کنشهای کنترلی یک اپراتور انسانی باتجربه و متخصص (بخش دانشبنیان)
- یافتن یک درونیابی هموار بین خروجیهای مجزا که معمولاً به صورت رایج به دست میآیند (بخش منطق فازی).
پس از کارهای اولیه، کاربرد کنترل فازی وسعت پیدا کرد. با این حال، دو انگیزه اصلی آن همچنان پابرجاست: ماهیت زبانی کنترل فازی آن را برای توضیح دانش فرایندی که باید کنترل شود یا رفتار کند ممکن میسازد. جنبه درونیابی کنترل فازی نیز منجر به دیدگاهی میشود که در آن، سیستمهای فازی به عنوان تقریب تابعی هموار دیده میشوند.
در اغلب موارد، از کنترلکننده فازی برای کنترل فیدبک استفاده میشود. هرچند، از آن میتوان در سطح نظارتی، مانند یک دستگاه خودتنظیم در یک کنترلکننده PID رایج نیز استفاده کرد. همچنین، کنترل فازی را میتوان از یک مدل فازی به دست آورد که از شناسایی سیستم به دست آمده است. اغلب کنترلکنندههای فازی به صورت زیر هستند:
- کنترلکننده ممدانی (زبانی) با نتایج فازی یا تک عنصری. این نوع کنترلکننده معمولاً به عنوان کنترلکننده حلقهبسته استفاده میشود.
- کنترلکننده تاکاگی-سوگنو (TS) که معمولاً به عنوان یک کنترلکننده نظارتی مورد استفاده قرار میگیرد.
کنترلکننده ممدانی
کنترلکننده ممدانی (Mamdani Controller) معمولاً به عنوان یک کنترلکننده فیدبک مورد استفاده قرار میگیرد.
از آنجایی که قاعدهمحوری یک نگاشت استاتیکی بین متغیرهای قبلی و بعدی است، باید از فیلترهای دینامیکی خارجی برای به دست آوردن رفتار دینامیکی مطلوب کنترلکننده استفاده کرد (شکل ۲).
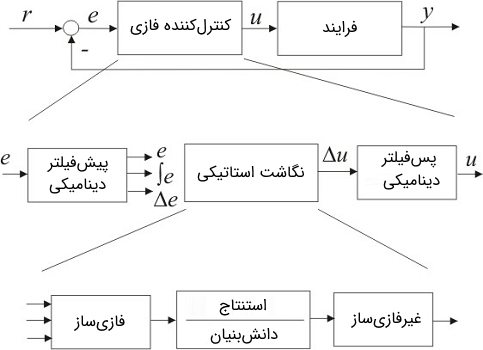
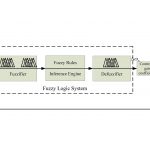
پروتکل کنترل به فرم قواعد اگر-آنگاه در پایگاه قواعد ذخیره میشود که بخشی از پایگاه دانش است. در حالی که قوانین مبتنی بر دانش کیفی هستند، توابع عضویتی که عبارات زبانی را تعریف میکنند، یک استنتاج هموار را برای متغیرهای فرایند عددی و نقاط تنظیم ارائه میدهند. فازیساز (Fuzzifier) درجات عضویت متغیرهای ورودی کنترلکننده را در مجموعههای فازی مرجع تعیین میکند. ساز و کار استنتاج یا همان موتور استنتاج این اطلاعات را با دانشِ ذخیره شده در قواعد ترکیب کرده و خروجی سیستم مبتنی بر قواعد را تعیین میکند. برای اهداف کنترل، یک سیگنال کنترل قطعی یا دقیق لازم است. غیرفازیساز (Defuzzifier) مقدار این سیگنال قطعی را از خروجیهای کنترلکننده فازی محاسبه میکند.
در شکل ۲، میتوان دید که نگاشت فازی تنها بخشی از کنترلکننده فازی است. پردازش سیگنال قبل و بعد از نگاشت فازی ضروری است. پیشفیلترها و پسفیلترها ورودیها و خروجیهای کنترلکننده را پردازش میکنند. این فیلترهای دینامیکی معمولاً مقیاسبندی سیگنال و فیلترسازی دینامیکی را انجام میدهند، مثلاً مشتق و انتگرال خطای کنترل یا سیگنال کنترل را محاسبه میکنند.
این تفکیک کنترلکننده به یک نگاشت استاتیکی (ایستا) و فیلترهای دینامیکی (پویا) را میتوان برای اغلب ساختارهای کنترل کلاسیک انجام داد. برای درک بهتر، یک کنترلکننده PID را در نظر بگیرید که معادله آن به صورت زیر است:
که در آن، سیگنال کنترلی است که به فرایند تحت کنترل اعمال میشود و سیگنال خطا، یعنی اختلاف بین خروجی مطلوب و خروجی اندازهگیری شده فرایند است. معادله (۱) یک تابع خطی (از نظر هندسی، یک ابرصفحه) است:
که در آن، ، ، و پارامترهای مربوط به بهرههای ، و هستند. فرم خطی (۲) را میتوان به یک تابع غیرخطی تعمیم داد:
در یک کنترلکننده منطق فازی، تابع غیرخطی با یک نگاشت فازی نمایش داده میشود. بدیهی است که کنترلکنندههای فازی را میتوان مشابه با کنترلکنندههای ، ، یا خطی، با استفاده از فیلترهای دینامیکی مناسب، مانند مشتقگیرها و انتگرالگیرها طراحی کرد.
ماهیت سیستمهای فازی ممدانی، بسیار نزدیک به ماهیت کنترل دستی است. این نوع کنترلکنندهها با مشخص کردن خروجی به ازای ترکیبهایی از سیگنالهای ورودی مختلف تعریف میشوند. هر ترکیب سیگنال ورودی به صورت قاعدهای به فرم زیر است:
: اگر به صورت باشد و ... و به صورت باشد، آنگاه به صورت است ().
در این کنترلکنندهها، ممکن است از بعضی رابطها یا عملگرهای دیگر، مانند «یا» (OR) یا «نه» (NOT) نیز استفاده شود. در سیستمهای فازی ممدانی، مجموعههای فازی مقدم (Antecedent) و مؤخر (Consequent) اغلب به صورت مثلثی یا گاوسی انتخاب میشوند. همچنین، رایج است که توابع عضویت ورودی، به گونهای با یکدیگر همپوشانی داشته باشند که مقادیر عضویت قاعده مقدم همیشه به ۱ جمع شوند (مجموعشان ۱ شود). در این حالت، و اگر پایگاه قواعد به فرم عطفی باشد، میتوان هر قاعده را به عنوان تعریف مقدار خروجی برای یک نقطه در فضای ورودی تفسیر کرد. این نقطه در فضای ورودی، با به دست آوردن مراکز مجموعههای فازی ورودی به دست میآید. در نتیجه، مقدار خروجی، مرکز مجموعه فازی خروجی است (روش مرکز مساحت).
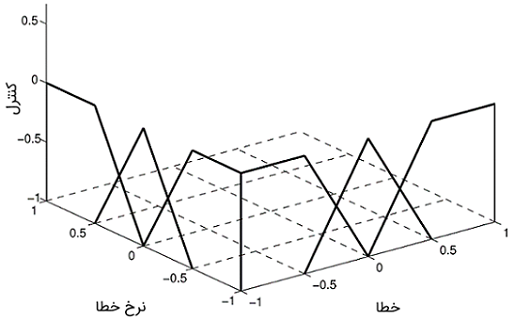
همانطور که در شکل ۳ نشان داده شده است، استدلال فازی، منجر به یک درونیابی نرم (هموار) بین نقاط فضای ورودی میشود.
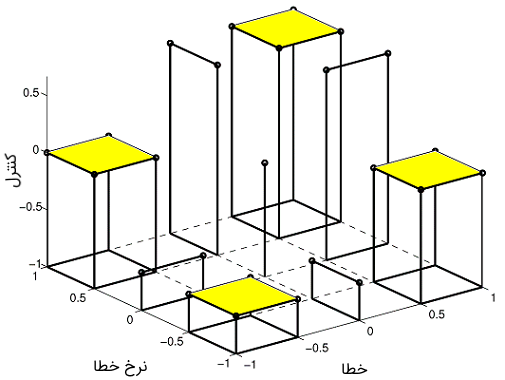
مثال: کنترلکننده PD فازی
همتای فازی یک کنترلکننده PD خطی را در نظر بگیرید. پایگاه قواعد دو ورودی (خطای و تغییر خطای ) و یک خروجی، یعنی قانون کنترل دارد. یک مثال از پایگاه قواعد در جدول زیر نشان داده شده است.
| PB | PS | ZE | NB | ||
| ZE | NS | NS | NB | NB | |
| PS | ZE | NS | NB | NS | |
| PB | PS | ZE | NB | ZE | |
| PB | PS | PS | NS | PS | |
| PB | PB | PS | ZE | PB | |
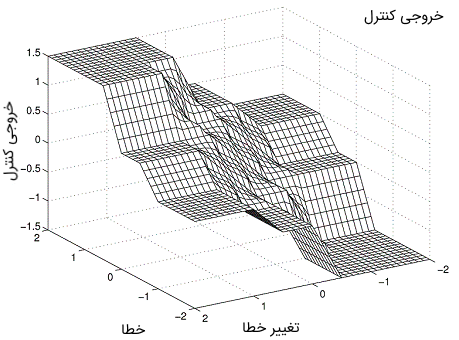
پنج عبارت زبانی (NB یعنی بسیار منفی، NS یعنی کمی منفی، ZE یعنی صفر، PS یعنی کمی مثبت و PB یعنی بسیار مثبت) برای هر متغیر استفاده میشود. هریک از درایههای جدول بالا یک قاعده را تعریف میکند. برای مثال، بیان میکند: «اگر کمی منفی (NS) و صفر (ZE) باشد، آنگاه کمی منفی (NS) است.» شکل 6 سطح کنترل حاصل را با ترسیم عمل کنترلی استنباطی برای مقادیر گسسته شده و نشان میدهد. در کنترل PD فازی، اختلاف اغلب به عنوان تقریبی برای مشتق استفاده میشود.
کنترل فازی تاکاگی-سوگنو
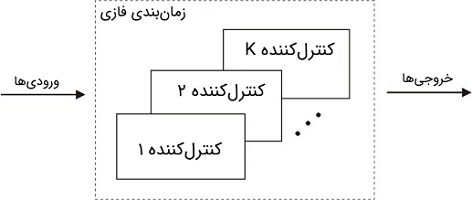
رویکرد کنترلکنندههای فازی تاکاگی-سوگنو (Takagi-Sugeno Controller) یا TS بسیار شبیه کنترلکنندههای زمانبندی بهره (Gain Scheduling) هستند.
در این روش، چندین کنترلکننده تعریف میشود که هریک از آنها در یک ناحیه خاص از فضای ورودی کنترلکننده معتبر است. خروجی کنترلکننده کلی با درونیابی کنترلکنندههای خطی محلی به دست میآید (شکل ۷).
مثالی از یک پایگاه قواعد کنترل TS به صورت زیر است:
- : اگر پایین باشد، آنگاه
- : اگر بالا باشد، آنگاه
در این مثال، متغیر مقدم، مرجع است، در حالی که متغیرهای مؤخر، به ترتیب، خطای و مشتق آن هستند. بنابراین، خروجی کنترلکننده ترکیبی خطی از و است، اما پارامترهای نگاشت خطی به مرجع بستگی دارند:
اگر کنترلکنندههای خطی فقط در پارامترهایشان با هم تفاوت داشته باشند، کنترلکننده TS یک فرم مبتنی بر قاعده از ساز و کار زمانبندی بهره است. در کنترل ناهمگن (Heterogeneous Control) میتوان از قوانین کنترل مختلف برای ناحیههای کاری متفاوت استفاده کرد. در مورد دوم، مثلاً کنترل بهینه زمان برای انتقالهای دینامیکی را میتوان با کنترل PD یا PID در مجاورت نقاط تعیین شده ترکیب کرد. بنابراین، کنترلکننده TS را میتوان یک نوع کنترل نظارتی در نظر گرفت.
کنترل نظارتی فازی
یک سیستم واسط فازی را میتوان در یک سطح بالاتر نظارتی از کنترل سلسلهمراتبی به کار برد. کنترلکننده نظارتی، یک کنترلکننده ثانویه است که کنترلکننده موجود را به گونهای تقویت میکند تا اهدافی که بدون نظارت امکان نخواهد داشت محقق شوند. برای مثال، یک کنترلکننده نظارتی میتواند پارامترهای یک کنترلکننده سطح پایین را بر اساس اطلاعات فرایند تنظیم کند (شکل ۸).
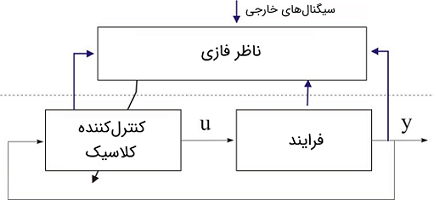
به این ترتیب، رفتار استاتیکی و دینامیکی سیستم کنترل سطح پایین را میتوان برای مقابله با غیرخطی بودن یا تغییرات در شرایط زیستمحیطی یا کاری اصلاح کرد. یک مزیت ساختار نظارتی این است که میتوان آن را به سیستمهای کنترل موجود قبلی افزود. از این رو، همیشه میتوان از کنترلکنندهای اصلی (اولیه) به عنوان کنترلکنندههای اولیه استفاده کرد و کنترلکننده نظارتی را به گونهای تنظیم نمود که عملکرد آن بهبود یابد.
یک ساختار نظارتی را میتوان برای پیادهسازی استراتژیهای کنترلی مختلف در یک کنترلکننده تکی به کار برد.
یک مثال، انتخاب کنترلکننده تناسبی با یک بهره بالا در هنگامی است که سیستم بسیار دور از سیگنال مرجع مطلوب باشد و کنترل PI را در نزدیکی سیگنال مرجع سوئیچ کند. از آنجایی که پارامترها برای هر پاسخ دینامیکی تغییر کردهاند، کنترلکنندههای نظارتی در حالت کلی غیرخطی هستند.
بسیاری از فرایندهای صنعتی با کنترلکنندههای PID کنترل میشوند. علیرغم مزایای این کنترلکنندهها، وقتی شرایط عملکرد تغییر کند، باید دوباره آنها را تنظیم کرد. این عیب را میتوان با استفاده از یک ناظر فازی برای تنظیم پارامترهای کنترلکننده سطح پایین رفع کرد. بدین ترتیب، میتوان مجموعهای از قواعد را از خبرهها برای تنظیم بهرههای و یک کنترلکننده PD، برای مثال بر اساس نقطه تنظیم فعلی ، به دست آورد. قواعد میتوانند اینگونه باشند: اگر خروجی فرایند بالا باشد، آنگاه کمی بهره تناسبی را کاهش بده و به اندازه متوسط بهره مشتقی را زیاد کن.
کنترلکننده TS را میتوان به عنوان یک نسخه ساده از کنترل نظارتی در نظر گرفت. به عنوان مثال، قواعد تاکاگی-سوگنوی شکل ۸ را میتوان برحسب قواعد ممدانی یا یگانه (Singleton) نوشت که خروجیهای آنها پارامترهای و است. این کنترلکنندهها در مسیر یک کنترلکننده PD استاندارد در یک سطح پایینتر قرار داده میشوند.
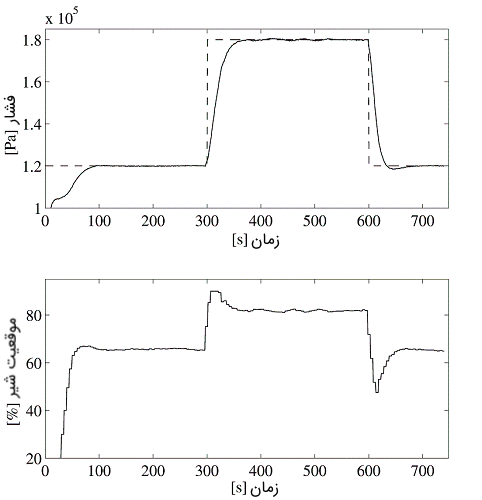
مثال: کنترل فشار
یک کنترلکننده فازی نظارتی برای کنترل فشار یک مخزن تخمیر آزمایشگاهی در شکل ۹ نشان داده شده است.
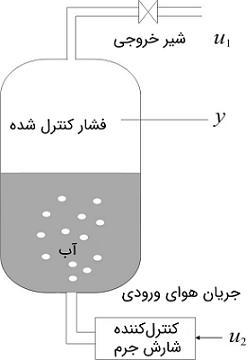
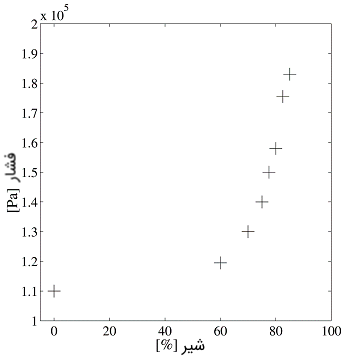
حجم مخزن تخمیر ۴۰ لیتر است که ۲۵ لیتر آب در آن قرار دارد. در ته مخزن هوا با آهنگ شارش ثابت به آب تزریق میشود و با یک کنترلکننده محلی شارش جرم ثابت نگه داشته میشود. فشار هوای بالای سطح آب با یک شیر خروجی در قسمت فوقانی مخزن کنترل میشود. با یک آهنگ شارش ورودی ثابت، سیستم یک ورودی تکی (موقعیت شیر) و یک خروجی تکی (فشار هوا) دارد. به دلیل ساز و کارهای فیزیکی اصلی و همچنین به دلیل رفتار غیرخطی شیر، فرایند یک مشخصه حالت ماندگار غیرخطی دارد که در شکل ۱۰ نشان داده شده است.
یک ناظر تکورودی-دوخروجی در شکل ۱۱ نشان داده شده است. ورودی ناظر، موقعیت شیر () است و خروجیهای آن، بهره تناسبی و انتگرالی یک کنترلکننده PI سنتی و رایج هستند. ناظر در هر نمونهبرداری از حلقه کنترل سطحپایین (۵ ثانیه) بهرههای PI را بهروز میکند.
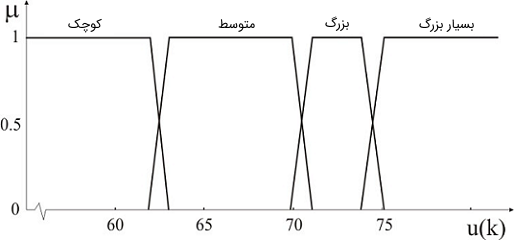
دامنه موقعیت شیر بین ۰ تا ۱۰۰ است و با توابع عضویت کوچک، متوسط، بزرگ و خیلی بزرگ مدل شده است (شکل ۱۲).
 " width="514" height="240">
" width="514" height="240">بهرههای P و I کنترلکننده PI متناظر با هریک از مجموعههای فازی هستند که به صورت زیر داده شدهاند.
| بسیار بزرگ | بزرگ | متوسط | کوچک | / بهرهها |
| ۱۴۰ | ۱۵۵ | ۱۷۰ | ۱۹۰ | |
| ۵۰ | ۷۰ | ۹۰ | ۱۵۰ |
مقادیر و از طریق شبیهسازی در ناحیههای متناظر با موقعیتهای شیر به دست میآیند. خروجی کلی ناظر به عنوان یک میانگین وزندار از بهرههای محلی محاسبه میشود. کنترلکننده فازی نظارتی، در شرایط نامی، در شبیهسازیها تنظیم و آزمایش شده و مستقیماً (بدون تنظیمات اضافه) به فرایند اعمال میشود. نتایج کنترل زمانحقیقی در شکل ۱۳ نشان داده شدهاند.
کنترل فازی مبتنی بر مدل
اگرچه کنترل فازی در ابتدا به عنوان یک روش طراحی کنترل فارغ از مدل و مبتنی بر دانش یک اپراتور انسانی بود، پژوهشهای کنونی تقریباً به روشهای کنترل فازی مدلبنیان اختصاص یافتهاند و میتوانند پایداری و قوام سیستم حلقهبسته را تضمین کنند.
در این رویکرد فرض میشود که یک مدل فازی در دسترس است و فرایندی را که باید کنترل شود توصیف میکند. سپس یک کنترلکننده فازی طراحی میشود که ساختار آن با ساختار مدل سیستم منطبق است. این ایده که برای سیستمهای فازی TS، موسوم به جبرانسازی توزیع شده موازی است، بسیار مثمر ثمر بوده است.
برای شرح این رویکرد، مدل تاکاگی-سوگنوی پیوسته (CTS) به فرم فضای حالت زیر را در نظر بگیرید:
که در آن، درجات تحقق قوانین (تعیین شده با درجات عضویت) هستند و در شرایط جمع محدب صدق میکنند و ، و ماتریسهای مدل فضای حالت محلیاند که فرض میشود مشاهدهپذیر و کنترلپذیر است. قانون جبرانسازی توزیع شده موازی (PDC) برای سیستم (۶) به صورت زیر است:
هدف، طراحی با در نظر گرفتن یک قانون کنترل مقاوم است. توابع اسکالر بالا و ماتریسهای متقارن را در نظر بگیرید. مسائل طراحی کنترل مختلفی را میتوان بیان کرد؛ مثلاً یافتن حداقل شرایط محافطهکارانهای که نامساوی زیر را تضمین میکند:
بر همین اساس، روشهای ترکیبی مختلفی ارائه شدهاند.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای سیستمها و منطق فازی
- آموزش سیستمهای فازی در متلب
- مجموعه آموزشهای مهندسی کنترل
- آموزش کنترل هوشمند با متلب
- سیستم کنترل حلقه باز — به زبان ساده
- تقلب نامه (Cheat Sheet) کنترل خطی
- پاسخ سیستم مرتبه دوم — از صفر تا صد
^^












