ژیزمان در نقشه برداری چیست؟ – تعریف، فرمول و محاسبه – به زبان ساده
ژیزمان در نقشه برداری، زاویه ساعتگرد بین شمال شبکه با امتداد مورد نظر است. این زاویه، به عنوان معیاری برای تشخیص جهتگیری یا سمتِ امتدادهای روی زمین مورد استفاده قرار میگیرد. ژیزمان، ارتباط بسیار نزدیکی با دیگر زاویههای مهم در نقشهبرداری دارد. آزیموت، زاویه حامل و ژیزمان معکوس، از جمله زاویههای مرتبط با ژیزمان هستند. در این مقاله، قصد داریم به تعریف ژیزمان در نقشه برداری، نحوه محاسبه آن را به همراه حل چند مثال و تمرین میپردازیم. علاوه بر این، رابطه بین ژیزمان با دیگر زاویهها نظیر ژیزمان معکوس، زاویه حامل و آزیموت را مورد بررسی قرار میدهیم.

نقشه برداری چیست ؟
«نقشهبرداری» (Surveying)، علم و هنر اندازهگیری موقعیت نسبی نقاط یا جزئیات عوارض زیر یا روی سطح زمین است. دادههای حاصل از نقشهبرداری، به منظور نمایش ویژگیهای زمین بر روی کاغذ پیاده میشوند و در اغلب پروژههای مهندسی مورد استفاده قرار میگیرند. نقشهبرداری، یکی از گرایشهای مهم رشته مهندسی عمران است. با این وجود، مبانی آن در اجرای تمام پروژههای مرتبط با زمین (معدنکاری، زمینشناسی، اکتشاف و ساخت و ساز)، کاربرد دارد. یکی از اصول نقشهبرداری، تعیین موقعیت و امتدادهای مبنا است.
تعیین موقعیت در نقشه برداری چیست ؟
«تعیین موقعیت» (Positioning)، مشخص کردن مختصات نقاط دلخواه روی زمین در یک دستگاه مختصات معلوم است. این دستگاه مختصات، باید دارای مبدا، محور، امتداد مبنا و دیگر پارامترهای تعیین موقعیت باشد.
امتداد مبنا در نقشه برداری چیست ؟
امتداد مبنا یا «خط مبنا» (Reference Line)، یک امتداد اختیاری و ثابت است که به منظور توجیه نقشه در منطقه یا تعیین موقعیت امتدادهای دیگر مورد استفاده قرار میگیرد. نصفالنهار جغرافیایی، نصفالنهار مغناطیسی و شمال شبکه (محور Y در صفحه)، از رایجترین امتدادهای مبنا محسوب میشوند. امتداد شمال شبکه در تعیین ژیزمان کاربرد دارد.
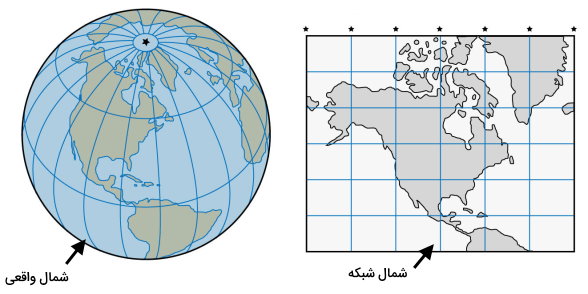
امتداد شمال شبکه چیست ؟
«شمال شبکه» (Grid North)، امتداد شمال در شبکه متعامد نقشهها است. این امتداد، با علامت GN (مخفف عبارت انگلیسی شمال شبکه) مشخص میشود. تصویر زیر، مقایسه بین شمال واقعی (شمال جغرافیایی) و شمال شبکه را نمایش میدهد.
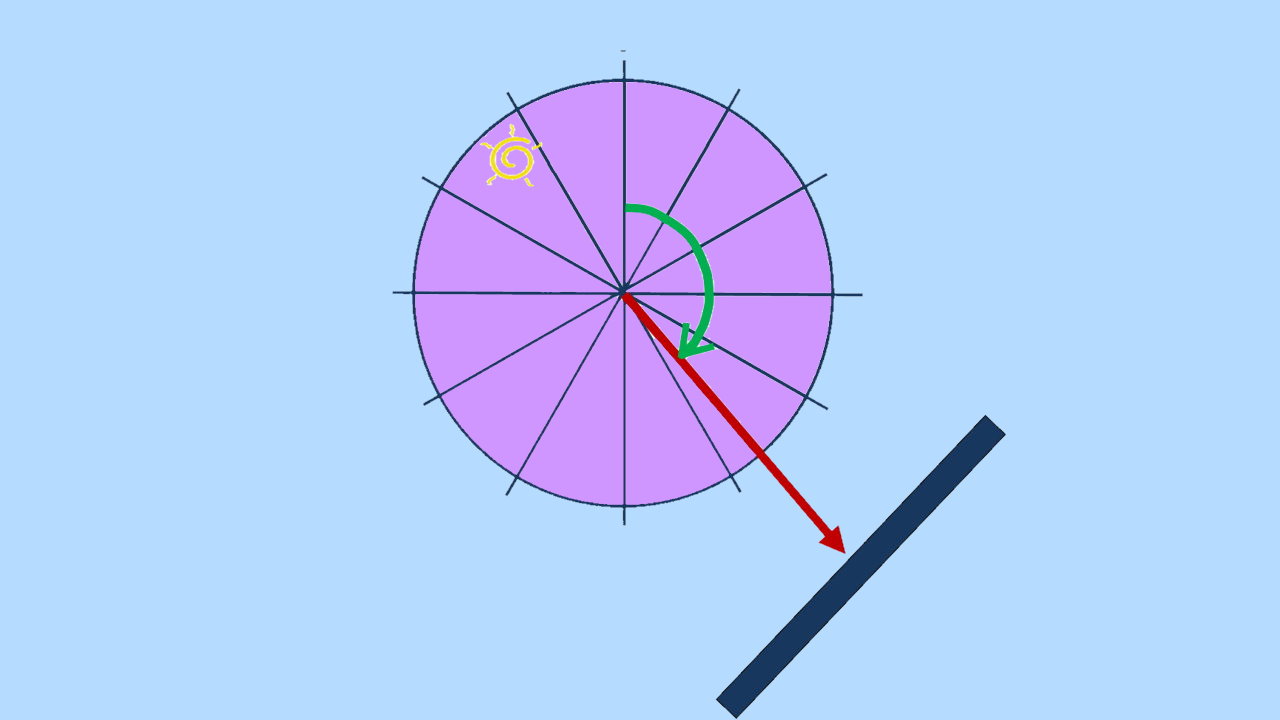
ژیزمان در نقشه برداری چیست ؟
«ژیزمان» (Gisement)، زاویه بین امتداد مورد نظر با امتداد شمال شبکه است. این زاویه، در جهت حرکت عقربههای ساعت (جهت ساعتگرد) اندازهگیری میشود. ژیزمان، به عنوان یک زاویه در تعیین جهت یا سمتِ امتدادهای روی زمین مورد استفاده قرار میگیرد. این امتدادها، نسبت به شمال شبکه سنجیده میشوند.
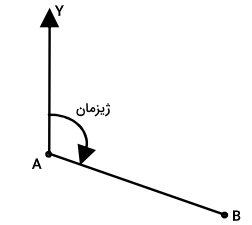
به عنوان مثال، تصویر بالا در نظر بگیرید. در این تصویر، امتداد AY، جهت شمال شبکه را نمایش میدهد. مطابق با تعریف، زاویه بین این امتداد با امتداد AB در جهت حرکت عقربههای ساعت، ژیزمان AB است.
ویژگی های ژیزمان در نقشه برداری چه هستند ؟
بر اساس تعریف، ژیزمان سه ویژگی دارد:
- ژیزمان، یک زاویه افقی است و در یک سطح افقی سنجیده میشود.
- امتداد مبنای اندازهگیری ژیزمان، شمال شبکه است.
- جهت اندازهگیری ژیزمان، ساعتگرد است.
ژیزمان در نقشه برداری چگونه نمایش داده می شود ؟
ژیزمان در نقشهبردای، با استفاده از حرف انگلیسی G و نقاط انتهایی امتداد مورد نظر نشان داده میشود. به عنوان مثال، در تصویر زیر، AY، امتداد شمال شبکه و AB، یک امتداد دلخواه را نمایش میدهد. ژیزمان AB، زاویهای است که امتداد AY با امتداد AB در جهت ساعتگرد میسازد.
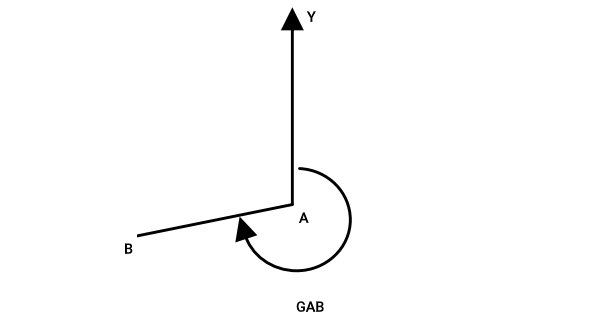
در نقشهبرداری، علامت GAB، بیانگر ژیزمان امتداد AB نسبت به AY است. ترتیب حروف در نمایش ژیزمان اهمیت دارد. به عنوان مثال، GAB، بیانگر ژیزمان معمولی و GBA، معرف ژیزمان معکوس است.
در رابطه با دروس تئوری و نرمافزارهای کاربردی حوزه نقشهبرداری و فتوگرامتری، فرادرس، چندین فیلم آموزشی جامع و کاربردی را تهیه کرده است که میتوانند شما را در یادگیری این مبحث کمک کنند. لینک مشاهده این فیلمها در ادامه آورده شده است.
- برای مشاهده مجموعه فیلمهای آموزش فتوگرامتری و نقشهبرداری + اینجا کلیک کنید.
ژیزمان معکوس چیست ؟
اگر محل قرارگیری امتداد مبنا را از روی نقطه ابتدایی امتداد مورد نظر به روی نقطه انتهایی آن انتقال دهیم، اندازه زاویه بین امتداد مبنا و امتداد مورد نظر در جهت ساعتگرد، ژیزمان معکوس خواهد بود. به عنوان مثال، دو نقطه A و B را در نظر بگیرید. فرض میکنیم نقطه A، ابتدا و نقطه B، انتهای امتداد خط واصل این دو نقطه است.
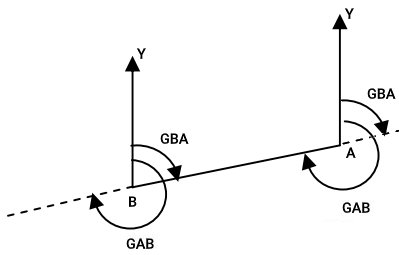
بر اساس تصویر بالا، در صورت در نظر گرفتن امتداد مبنا بر روی نقطه ابتدایی A، اندازه زاویه ساعتگرد بین AY و AB، به عنوان ژیزمان اصلی (GAB) و زاویه ساعتگرد بین AY و ادامه BA (خطچین)، به عنوان ژیزمان معکوس در نظر گرفته میشود. در صورت در نظر گرفتن امتداد مبنا بر روی نقطه انتهایی B، اندازه زاویه ساعتگرد بین BY و AB، به عنوان ژیزمان معکوس (GBA) و زاویه ساعتگرد بین BY و ادامه AB (خطچین)، به عنوان ژیزمان در نظر گرفته میشود.
رابطه بین ژیزمان و ژیزمان معکوس چیست ؟
امتداد بین دو نقطه، همواره با یکدیگر زاویه نیمصفحه (زاویه ۱۸۰ درجه) میسازند. ژیزمان معکوس، از جمع یا تفریق این زاویه با ژیزمان اصلی به دست میآید. رابطه بین ژیزمان ژیزمان معکوس، به صورت زیر نوشته میشود:
اگر اندازه ژیزمان، کوچکتر از ۱۸۰ درجه باشد، ژیزمان معکوس از جمع ژیزمان و زاویه ۱۸۰ درجه به دست میآید:
اگر اندازه ژیزمان، بزرگتر از ۱۸۰ درجه باشد، ژیزمان معکوس برابر با اختلاف ژیزمان و زاویه ۱۸۰ درجه میشود:
با توجه به روابط بالا میتوانیم نتیجه بگیریم که اندازه ژیزمان معکوس، همواره بین ۰ تا ۱۸۰ درجه است.
رابطه بین ژیزمان و ژیزمان معکوس بر حسب گرادیان
اگر اندازه ژیزمان بر حسب گرادیان داده شد، از رابطه زیر برای تعیین ژیزمان معکوس استفاده میکنیم:
برای امتدادی با ژیزمان بزرگتر از ۲۰۰ گرادیان، از علامت منفی (-) و برای امتدادی با ژیزمان کوچکتر از ۲۰۰، از علامت مثبت (+) در رابطه بالا استفاده میشود. اندازه ژیزمان معکوس، همواره بین ۰ تا ۲۰۰ گرادیان قرار دارد.
مثال ۱: محاسبه ژیزمان معکوس از روی ژیزمان
ژیزمان یک امتداد، برابر با ''۴۳'۲۱°۱۹۰ است. ژیزمان معکوس را به دست بیاورید.
فرمول ژیزمان معکوس، با توجه به اندازه ژیزمان نوشته میشود. در اینجا، ژیزمان امتداد، از ۱۸۰ درجه بیشتر است. بنابراین، ژیزمان معکوس از رابطه زیر به دست میآید:
مقدار ژیزمان را به جای GAB درون رابطه بالا قرار میدهیم:
در نتیجه، ژیزمان معکوس برابر با ''۴۳'۲۱°۱۰ است.
مثال 2: محاسبه ژیزمان از روی ژیزمان معکوس
ژیزمان امتداد AB با ، کدام گزینه است؟
صورت سوال، ژیزمان AB را از ما میخواهد اما مقدار ژیزمان برای امتداد BA یا همان GBA را به ما داده است. این مقدار، ژیزمان معکوس را نمایش میدهد. به دلیل بیان اندازه ژیزمان معکوس بر حسب گرادیان (g)، از فرمول زیر به منظور محاسبه ژیزمان استفاده میکنیم:
از آنجایی که نمیدانیم ژیزمان AB از ۲۰۰ گرادیان کوچکتر یا بزرگتر است، محاسبات را برای هر دو حالت (علامت منفی و علامت مثبت) انجام میدهیم. به این منظور، ابتدا علامت منفی را برای رابطه بالا در نظر میگیریم:
ژیزمان هر امتداد، بین ۰ تا ۴۰۰ گرادیان (۰ تا ۳۶۰ درجه) قرار دارد. بنابراین، ژیزمان امتداد AB نمیتواند ۵۵۰ گرادیان باشد. اکنون، سوال را با استفاده از رابطه بین ژیزمان و معکوس ژیزمان با علامت مثبت حل میکنیم:
حاصل رابطه بالا، ۱۵۰ گرادیان شد. این زاویه، بین ۰ تا ۴۰۰ گرادیان (محدوده موجه ژیزمان) قرار دارد. بنابراین، ژیزمان امتدادی با معکوس ۳۵۰ گرادیان، برابر با ۱۵۰ گرادیان است.
زاویه حامل در نقشه برداری چیست ؟
به کوچکترین زاویهای که یک امتداد با محور Yها (امتداد شمال شبکه) میسازد، زاویه حامل یا اصطلاحا «بیرینگ» (Bearing) میگویند. این زاویه، همواره بین ۰ تا ۹۰ درجه (۰ تا ۱۰۰ گرادیان) قرار دارد. تصویر زیر، تفاوت بین ژیزمان و زاویه حامل را نمایش میدهد.
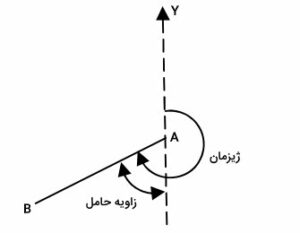
همانطور که در تصویر بالا مشاهده میشود، اندازهگیری زاویه حامل، لزوما به صورت ساعتگرد نیست؛ چراکه مقدار این زاویه، با توجه به کوچکترین زاویه بین امتداد مورد نظر و امتداد شمال شبکه به دست میآید و به جهت اندازهگیری بستگی ندارد.
زاویه حامل در نقشه برداری چگونه نمایش داده می شود ؟
زاویه حامل در نقشه برداری، با حرف انگلیسی V و عنوان نقاط ابتدایی و انتهایی امتداد مورد نظر نمایش داده میشود. به عنوان مثال، نقاط A و B در تصویر زیر را در نظر بگیرید. زاویه بین امتداد این دو نقطه با شمال شبکه (زاویه VAB)، همان زاویه حامل است.
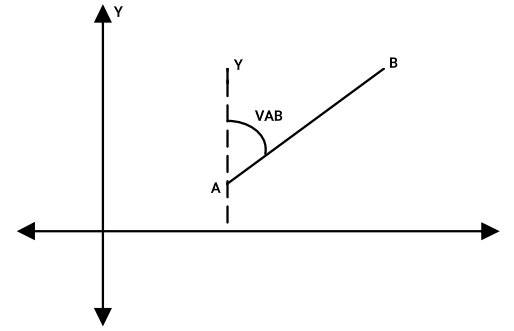
در مثال بالا، مقدار زاویه حامل با ژیزمان برابری میکند. با این وجود، این اتفاق تنها زمانی رخ میدهد که امتداد مورد نظر (امتداد AB) در ربع اول محورهای مختصات قرار گرفته باشد. برای مشخص کردن ربع قرارگیری زاویه حامل، میتوانیم مقدار آن را بین علائم معرف جهتهای اصلی قرار دهیم. به عنوان مثال، امتداد AB، در ربع اول قرار دارد.
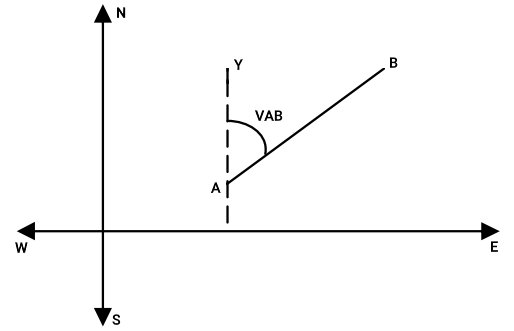
ربع اول، محدوده بین جهتهای شمال (N) و شرق (E) را دربرمیگیرد. از اینرو، زاویه حامل امتداد AB، به صورت زیر نمایش داده میشود:
اگر زاویه حامل برابر با ۴۵ درجه بود، آن را به شکل زیر نمایش میدادیم:
اگر زاویه حامل با همین اندازه در ربع سوم (محدوده بین جهتهای جنوب S و غرب W) قرار میگرفت، نمایش آن به صورت زیر تغییر میکرد:
زاویه حامل چگونه محاسبه می شود ؟
محاسبه زاویه حامل، با توجه به مختصات نقاط ابتدایی و انتهایی امتداد مورد نظر انجام میگیرد. به عنوان مثال، امتداد AB را در نظر بگیرید. قصد داریم اندازه زاویه حامل این امتداد (VAB) را به دست بیاوریم. اختلاف نقاط ابتدایی (A) و انتهایی (B) در راستای محور Y، با علامت ΔY و اختلاف بین آنها در راستای محور X، با علامت ΔX نمایش داده میشود. با رسم این اندازهها، یک مثلث قائمالزاویه به وجود میآید.

بر اساس قواعد حاکم بر مثلثهای قائمالزاویه (روابط مثلثاتی)، اندازه زاویه حامل برابر میشود با:
به عبارت دیگر، اگر قدر مطلق معکوس تانژانت یا آرک تانژانت را برای نسبت اختلاف افقی به اختلاف عمودی دو نقطه به دست بیاوریم، در واقع زاویه حامل امتداد آن دو نقطه را تعیین کردهایم.
مثال ۳: تعیین زاویه حامل از روی مختصات
مختصات دو نقطه با عنوانهای A و B عبارت است از:
زاویه حامل امتداد AB را تعیین کنید.
به منظور تعیین زاویه حامل، باید اختلاف نقاط ابتدایی و انتهایی امتداد مورد نظر را در راستای X و Y به دست بیاوریم. مختصات این نقاط، عبارت هستند از:
اختلاف A و B در راستای X، به صورت زیر محاسبه میشود:
اکنون میتوانیم برای تعیین زاویه حامل، از رابطه زیر استفاده کنیم:
تانژانت زاویه برابر با ۰/۶۲۵ میشود. بنابراین، جواب رابطه بالا (اندازه زاویه حامل) برابر است با:
امکان تعیین زاویه حامل با استفاده از ژیزمان نیز وجود دارد که در بخش بعدی به آن میپردازیم.
رابطه بین زاویه حامل و ژیزمان در نقشه برداری چیست؟
رابطه بین زاویه حامل و ژیزمان در نقشه برداری، با توجه به ربع قرارگیری امتداد مورد نظر تعیین میشود. جدول زیر، این رابطه را برای زاویههای اندازهگیری شده بر حسب درجه نمایش میدهد.
| ربع قرارگیری امتداد مورد نظر | نحوه نمایش زاویه حامل | فرمول زاویه حامل |
| ربع اول | NVE | |
| ربع دوم | SVE | |
| ربع سوم | SWE | |
| ربع چهارم | NWE |
در صورت اندازهگیری زوایا بر حسب رادیان، رابطه بین ژیزمان و زاویه حامل مطابق با جدول زیر خواهد بود.
| ربع قرارگیری امتداد مورد نظر | نحوه نمایش زاویه حامل | فرمول زاویه حامل |
| ربع اول | NVE | |
| ربع دوم | SVE | |
| ربع سوم | SWE | |
| ربع چهارم | NWE |
به کمک روابط ارائه شده در جداول بالا و مختصات دو نقطه ابتدایی و انتهایی امتداد مورد نظر، میتوانیم زاویه حامل و سپس ژیزمان امتداد را به دست بیاوریم. البته برای این کار، به یک جدول دیگر نیز نیاز داریم. این جدول، به منظور تعیین ربع قرارگیری امتداد، بر اساس علامت ΔX و ΔY مورد استفاده قرار میگیرد.
| ربع قرارگیری امتداد مورد نظر | علامت ΔX | علامت ΔY |
| ربع اول | + | + |
| ربع دوم | + | - |
| ربع سوم | - | - |
| ربع چهارم | - | + |
برای سنجش خود و اطمینان از یادگیری مطالب ارائه شده، سوال زیر را حل کنید.
تمرین و آزمون
نقاط A و B با مختصات زیر را در نظر بگیرید:
ربع قرارگیری، زاویه حامل و ژیزمان امتداد AB به ترتیب کدامیک از گزینههای زیر است؟
ربع دوم، ۲۲۵ درجه، ۴۵ درجه
ربع چهارم، ۴۵ درجه، ۳۱۵ درجه
ربع دوم، ۴۵ درجه، ۳۱۵ درجه
ربع چهارم، ۲۲۵ درجه، ۴۵ درجه
حل سوال را با تعیین ربع قرارگیری امتداد AB شروع میکنیم. مختصات نقاط ابتدایی و انتهایی AB عبارت هستند از:
با توجه به این مختصات داریم:
علامت ΔX، منفی و علامت ΔY، مثبت است. بنابراین، امتداد AB به ربع چهارم محورهای مختصات اشاره دارد. بر اساس مقادیر ΔX و ΔY، میتوانیم زاویه حامل را توسط رابطه زیر به دست بیاوریم:
تانژانت زاویه ۴۵ درجه برابر با ۱ میشود. از اینرو، زاویه حامل امتداد AB برابر با ۴۵ درجه است:
اکنون، با استفاده از مقدار زاویه حامل و ربع قرارگیری امتداد AB، امکان محاسبه ژیزمان فراهم میشود. امتداد AB، در ربع چهارم قرار دارد. به همین دلیل، رابطه آن با زاویه حامل عبارت است از:
مقدار زاویه حامل را در رابطه بالا قرار میدهیم و آن را بر حسب ژیزمان حل میکنیم:
در نتیجه، ژیزمان امتداد AB برابر با ۳۱۵ درجه است.
محاسبه ژیزمان در نقشه برداری چگونه است ؟
در نقشهبرداری، محاسبه ژیزمان امتدادهای متوالی، مانند امتداد ضلعها در پیمایش بسته، به طور مجاز انجام نمیگیرد. در اغلب موارد، این زاویهها با استفاده از یک ژیزمان معلوم به دست میآید. به عبارت دیگر، در صورت معلوم بودن ژیزمان یک امتداد و زاویه راس مجاور آن، امکان محاسبه ژیزمان امتداد بعدی فراهم میشود. به عنوان مثال، دو ضلع متوالی AB و AC را در نظر بگیرید.
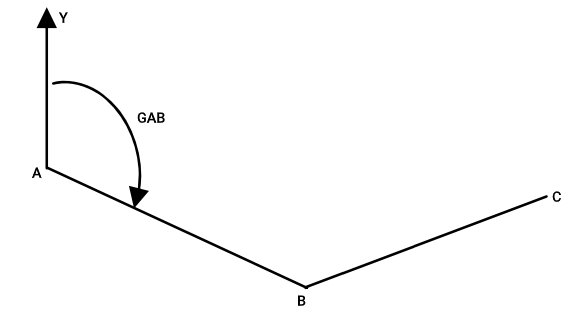
راستای Y، امتداد مبنای اندازهگیری ژیزمان (شمال شبکه) را نمایش میدهد. از اینرو، زاویه GAB، همان ژیزمان امتداد ضلع AB است.
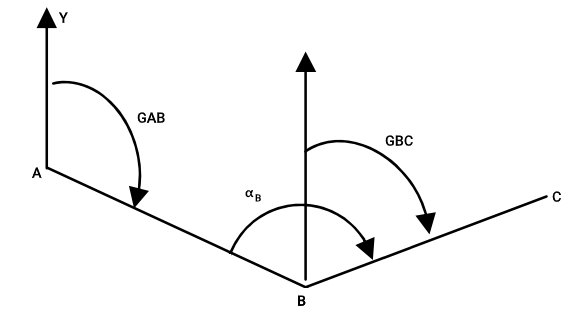
اگر زاویه راس B (زاویه بین ضلعهای AB و BC) را برابر با αB باشد، اندازه ژیزمان امتداد ضلع BC از رابطه زیر به دست میآید:
در صورت اندازهگیری بر اساس گرادیان، رابطه بالا به شکل زیر نوشته میشود:
به فرآیند استفاده از ژیزمان یک امتداد برای به دست آوردن ژیزمان امتداد مجاور، انتقال ژیزمان میگویند.
اثبات رابطه انتقال ژیزمان
اثبات رابطه انتقال ژیزمان، بسیار ساده است. به این منظور، ضلع با ژیزمان معلوم را ادامه میدهیم. اندازه زاویه بین امتداد ضلع مجاور (ضلع با ژیزمان نامعلوم) را برابر با Δ در نظر میگیریم.

با توجه به زوایای نمایش داده شده در تصویر بالا، داریم:
رابطه دوم را بر حسب Δ بازنویسی میکنیم:
سپس، این رابطه را درون رابطه اول قرار میدهیم:
به این ترتیب، ژیزمان امتداد ضلع BC برابر میشود با:
مثال ۴: محاسبه ژیزمان یک ضلع از پیمایش بسته
در یک پیمایش بسته، ژیزمان ضلعی با نقطه ابتدایی A و نقطه انتهایی B برابر با ۱۰۵/۳۱۵۴ گرادیان است. اگر زاویه راستگرد راس B، برابر با ۱۳۱/۱۵۴۷ گرادیان باشد، ژیزمان ضلع BC برابر با چند گرادیان میشود؟
در این مثال، قصد داریم ژیزمان یک ضلع را با توجه به ژیزمان ضلع مجاورش به دست بیاوریم. به دلیل بیان زاویهها بر حسب گرادیان، رابطه مورد استفاده برای تعیین ژیزمان ضلع مجهول عبارت است از:
- : ژیزمان ضلع مورد نظر
- : ژیزمان معلوم و مجاور BC برابر با ۱۰۵/۳۱۵۴ گرادیان
- : زاویه راس B یا زاویه بین امتداد معلوم و مجهول برابر با ۱۳۱/۱۵۴۷ گرادیان
مقادیر معلوم را درون رابطه بالا قرار میدهیم:
در نتیجه، ژیزمان ضلع BC برابر با ۳۶/۴۷۰۱ گرادیان است.
محاسبه آنلاین ژیزمان
یکی از روشهای محاسبه ژیزمان یک امتداد بر اساس مختصات نقاط ابتدایی و انتهایی، استفاده از ابزارهای اینترنتی و وبسایتهای مخصوص این کار است. وبسایت OmniCalculator (+)، از گزینههای مناسب برای انجام ای محاسبات به شمار میرود. با وارد شدن به ماشینحساب آزیموت در این وبسایت، کادرهایی مشابه با کادرهای تصویر زیر به نمایش درمیآیند.
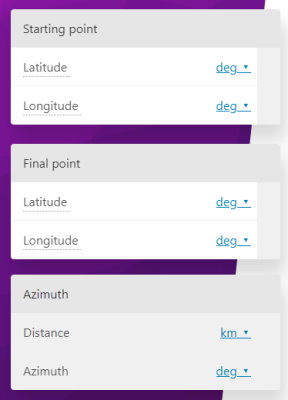
بخش «Starting Point»، به مختصات نقطه شروع امتداد و بخش «Final Point»، به مختصات نقطه پایان امتداد اختصاص دارد. با وارد کردن عرض جغرافیایی در کادر «Latitude» و طول جغرافیایی در کادر «Longitude»، طول ضلع بین نقطه ابتدایی و انتهایی در کادر «Distance» و اندازه ژیزمان امتداد ضلع در کادر «Azimuth» به نمایش درمیآید. یکی از ویژگیهای ابزار بالا، امکان تنظیم واحدهای ورودی و خروجی است. به این ترتیب، کاربر میتواند مختصات نقاط را بر حسب درجه یا گرادیان وارد کرده و ژیزمان را بر حسب درجه یا رادیان محاسبه کند.
معرفی مجموعه فیلم های آموزش نقشه برداری و فتوگرامتری
نقشهبردای، از فعالیتهای ثابت و مهم در حوزههای مرتبط با علوم زمین و مهندسی سازه است. برنامهریزی و امکانسنجی بسیاری از پروژههای مهندسی نظیر کشاورزی، معدنکاری، راهسازی، پلسازی، ساختمانسازی و غیره، بر اساس دادههای حاصل از عملیاتهای نقشهبرداری و فتوگرامتری انجام میگیرد. به دلیل اهمیت بالای این حوزه، فردارس، مجموعهای از آموزشهای تئوری و نرمافزاری را در زمینه دروس و مهارتهای ضروری نقشهبرداری تهیه کرده است. لینک مشاهده فیلمهای این مجموعه در ادامه آورده شده است.
- برای مشاهده مجموعه فیلمهای آموزش فتوگرامتری و نقشهبرداری + اینجا کلیک کنید.
تفاوت آزیموت و ژیزمان در چیست ؟
در برخی از موارد، ژیزمان با عنوان «آزیموت» (Azimuth) بیان میشود. تعریف آزیموت، شباهت بسیار زیادی به تعریف ژیزمان دارد. به زاویه افقی بین دو امتداد در جهت ساعتگرد، سمت یا آزیموت میگویند. امتداد مبنا برای اندازهگیری آزیموت، میتواند یک امتداد فرضی (دلخواه)، نجومی (جغرافیایی)، مغناطیسی، شبکه و هر امتداد دیگری باشد. به عنوان مثال، تصویر زیر را در نظر بگیرید. خطچینها، امتداد شمال واقعی (خطوط نصفالنهار جغرافیایی) را نمایش میدهند.
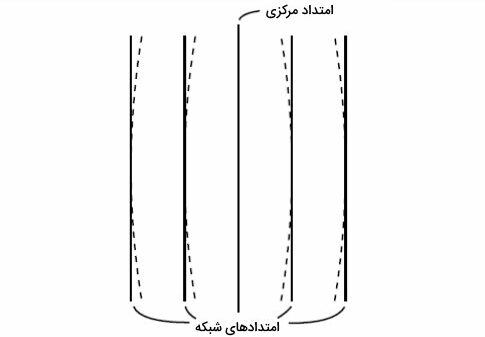
خطوط توپر، شمال شبکه هستند. یکی از این خطها، دقیقا با خط نصفالنهار مطابقت دارد. به این خط، امتداد مرکزی میگویند. امتدادهای شبکه، موازی با امتداد مرکزی رسم میشوند. در صورت اندازهگیری آزیموت بر اساس خطوط نصفالنهار جغرافیایی، مقدار آزیموت واقعی یا جغرافیایی به دست میآید. در صورت اندازهگیری آزیموت بر اساس خطوط شبکه، آزیموت شبکه یا همان ژیزمان به دست میآید.
در نهایت میتوانیم بگوئیم که ژیزمان، یکی از انواع آزیموت است. البته، اصطلاح آزیموت، بیشتر در علوم زمین، مخصوصا برداشتهای زمینشناسی کاربرد دارد. به عنوان مثال، زاویه و امتداد لایهبندیهای زمین، از اصلاح آزیموت استفاده میشود. در حوزه نقشهبرداری، ژیزمان، کاربرد و رواج بیشتری دارد.
سوالات متداول در رابطه با ژیزمان در نقشه برداری
در این بخش، به برخی از پرتکرارترین سوالات در رابطه با مبحث ژیزمان در نقشه برداری به طور خلاصه پاسخ میدهیم.
ژیزمان یعنی چه ؟
ژیزمان، یعنی زاویهای که هر امتداد با امتداد شمال شبکه در جهت ساعتگرد میسازد.
علامت ژیزمان چیست ؟
علامت ژیزمان، حرف انگلیسی G است.
امتداد مبنای اندازه گیری ژیزمان چیست ؟
شمال شبکه، مبدا اندازهگیری یا همان امتداد مبنای ژیزمان است.
ژیزمان در نقشه برداری چند درجه است ؟
زاویه ژیزمان بین ۰ تا ۳۶۰ درجه یا ۰ تا ۴۰۰ گرادیان است.
ژیزمان معکوس در نقشه برداری چیست ؟
ژیزمان معکوس، زاویهای است که جمع یا اختلاف آن با ژیزمان، برابر با ۱۸۰ درجه میشود. اندازه این زاویه، بین ۰ تا ۱۸۰ درجه یا ۰ تا ۲۰۰ گرادیان است.
فرمول محاسبه ژیزمان معکوس در نقشه برداری چیست ؟
ژیزمان معکوس از فرمول «°۱۸۰ ± ژیزمان = ژیزمان معکوس» به دست میآید. برای ژیزمان بزرگتر از ۱۸۰ درجه از علامت منفی (-) و برای ژیزمان کوچکتر از ۱۸۰ درجه، از علامت مثبت (+) استفاده میکنیم.
آزیموت و ژیزمان در نقشه برداری چه تفاوتی دارند ؟
امتداد مبنای ژیزمان، شمال شبکه است؛ در حالی که امتداد مبنای آزیموت، میتواند شمال شبکه یا هر امتداد دیگری مانند نصفالنهار جغرافیایی، نصفالنهار مغناطیسی و غیره باشد.
تفاوت زاویه حامل ژیزمان در نقشه برداری چیست ؟
زاویه حامل، کوچکترین زاویهای است که یک امتداد با امتداد مبنا میسازد. ژیزمان، زاویه ساعتگرد بین امتداد مبنا با یک امتداد است. برخلاف ژیزمان، اندازهگیری این زاویه میتواند پادساعتگرد نیز باشد. ژیزمان بین ۰ تا ۳۶۰ درجه تغییر میکند؛ در صورتیکه بازه اندازه زاویه حامل بین ۰ تا ۹۰ درجه است.













بسیار مختصر و مفید
ممنون از شما