هموارسازی نمایی سری زمانی – راهنمای کاربردی

در طبیعت و دنیای اطراف ما، پدیده‌هایی وجود دارند که با طول زمان دچار تغییر می‌شوند. این تغییرات می‌تواند به عوامل مختلفی وابسته باشد. گاهی ممکن است یک روند صعودی (یا نزولی) در تغییرات مربوط به ویژگی‌های یک پدیده مشاهده شود یا تغییرات فصلی باعث پدید آمدن تفاوت و اختلاف شود. هدف تحلیل سری زمانی، تشخیص یا ایجاد یک مدل سری زمانی است که در آن، بخش تصادفی و بخش غیرتصادفی از یکدیگر جدا شده و قابل تشخیص شوند، بطوری که بتوان آینده آن پدیده تصادفی را به طور کلی مشخص کرد. از شیوه‌های جداسازی بخش تصادفی از غیرتصادفی، می‌توان به هموارسازی نمایی سری زمانی (Smoothing) اشاره کرد. هموارسازی نمایی سری زمانی تکنیکی است که به کمک آن هموارسازی صورت گرفته و داده‌های مربوط به گذشته، رفته رفته نقش کمتری در محاسبه میانگین خواهند داشت. این سیر نزولی به صورت نمایی تغییر کرده و در نتیجه به آن هموارسازی نمایی می‌گویند.

برای آشنایی بیشتر با مدل‌های سری زمانی و مفاهیم اولیه آن بهتر است نوشتار سری زمانی در علم داده — از صفر تا صد و تحلیل سری زمانی — تعریف و مفاهیم اولیه را مطالعه کنید. همچنین خواندن نوشتار سری زمانی در SPSS — راهنمای کاربردی و تحلیل سری زمانی با پایتون — معرفی انواع مدل ها نیز خالی از لطف نیست.

هموارسازی نمایی سری زمانی

به منظور مشخص کردن وضعیت داده‌های سری زمانی باید بخش تصادفی را از بخش غیرتصادفی جدا کرد. به این منظور باید مدل را ایستا (Stationary) نمود به این معنی که روند و تغییرات دیگری که ماهیت تصادفی ندارند را از داده‌ها خارج کرد. چنین عملی را هموارسازی (Smoothing) می‌نامند.

هموارسازی نمایی سری زمانی با میانگین متحرک (Exponentially Weighted Moving Average) یا EWMA، یک روش برای محاسبه میانگین از مقادیر، به طور پیوسته است. به این معنی که با ورود یک متغیر جدید، میانگین نیز تغییر خواهد یافت. اثر تغییری که مقدار جدید به میانگین وارد می‌کند به صورت «تابع نمایی کاهشی» (Decreasing Exponentially) از زمان است. به این معنی که اثر داده‌های دورتر روی میانگین متحرک کمتر و اثر داده‌های اخیر روی میانگین متحرک بیشتر است و این اثر به صورت نمایی تغییر می‌کند.

از مزایای استفاده از هموارسازی نمایی سری زمانی با میانگین متحرک می‌توان به سادگی و سرعت انجام محاسبات اشاره کرد.

در الگوریتم‌های EWMA از یک فاکتور کاهنده (Decay Factor) استفاده می‌شود که با علامت $$\alpha$$‌ مشخص می‌شود. هر چه $$\alpha$$ بزرگتر باشد، اهمیت و نقش داده‌های اخیر در تعیین و پیش‌بینی مقدارهای آینده بیشتر شده و اثر داده‌های گذشته کمرنگ‌تر می‌شود. این فاکتور مقداری در بازه $$(0,1)$$ دارد.

الگوریتم محاسباتی برای EWMA به شکل زیر خواهد بود.

1. مقدار $$x_t$$ را در مقدار $$\alpha$$ ضرب کنید.
2. مقدار میانگین متحرک در زمان $$t-1$$ را در $$(1-\alpha)$$ ضرب کنید.
3. حاصل جمع مرحله ۱ و ۲ را به عنوان مقدار زمان سری زمانی هموار شده در $$t$$ در نظر بگیرید.
4. عملیات را از مرحله ۱ تکرار نمایید.

فرض کنید که یک سری زمانی با ۵ مشاهده دارید که برحسب زمان در نمودار زیر ترسیم شده‌اند.

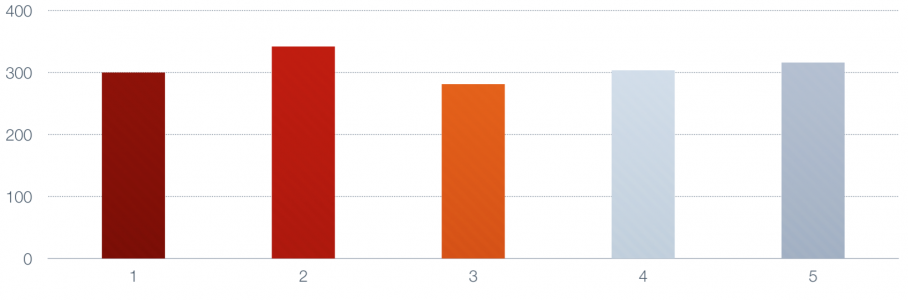
فرض کنید مقدار $$\alpha$$ برابر با $$0.5$$ در نظر گرفته شده است. می‌خواهیم مراحل هموارسازی میانگین متحرک را روی این داده‌ها اجرا کنیم.

در گام اول مشخص است که میانگین متحرک، همان مقدار اول است زیرا مشاهداتی قبل از آن وجود ندارد.

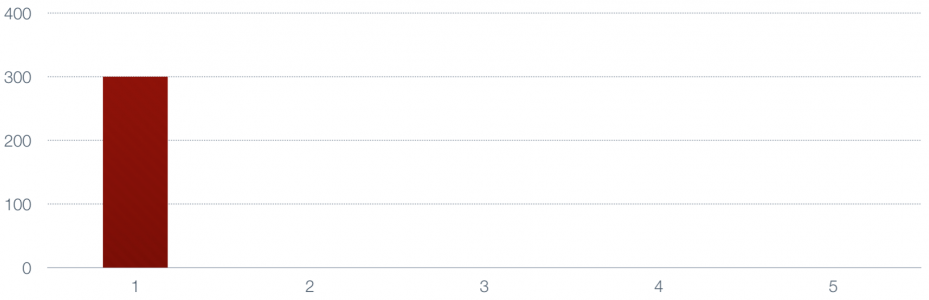
با گرفتن میانگین وزنی با وزن $$\alpha$$ بین مقدار مربوط به مشاهده اول و دوم، دومین نقطه هموارسازی ایجاد می‌شود.

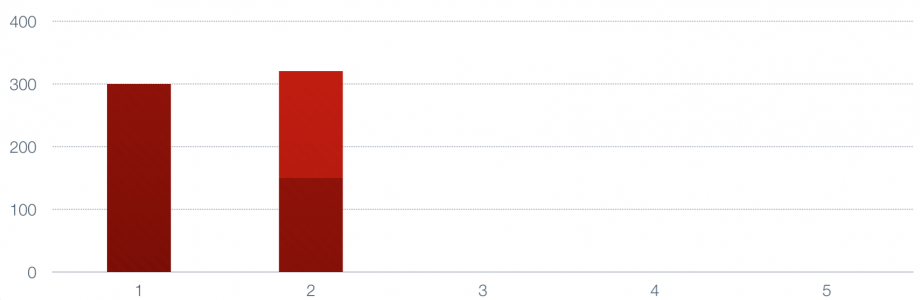
ارتفاع ستون جدید در نمودار، مقدار هموار شده را نشان می‌دهد. از آنجایی که سهم مشاهده اول و دوم در محاسبه این میانگین یکسان است، ارتفاع این مستطیل به طور مساوی بین دو رنگ قرمز پررنگ و کم‌رنگ تقسیم شده است.

حال نقطه سوم الی آخر را برای مقادیر هموار شده محاسبه و در نمودار ترسیم می‌کنیم. رنگ هر قسمت در ستون مربوط به نقاط هموار شده بیانگر سهم آن نقطه در محاسبه میانگین متحرک است.

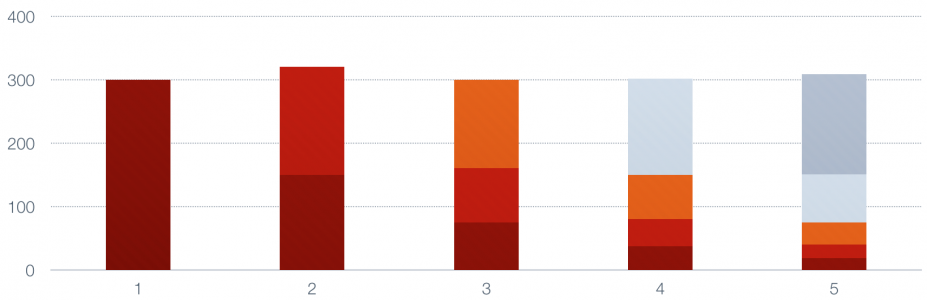
همانطور که مشخص است، سهم مشاهده اول که با رنگ قرمز پررنگ مشخص شده، در محاسبه نقاط هموار شده با روش هموارسازی نمایی میانگین متحرک به صورت نمایی رو به کاهش است. از طرفی در نقطه آخر، سهم مشاهده پنجم، نصف سهم بقیه نقاط است.

در تصویر زیر این تغییر نمایی برای وزن یا اثر مشاهده اول روی مشاهدات دیگر مشخص شده است.

در ادامه به رابطه‌ای که برای محاسبه هموارسازی نمایی میانگین متحرک احتیاج داریم، اشاره خواهیم کرد. همچنین مشخصات داده‌هایی که می‌توانیم برایشان مدل‌سازی انجام دهیم، مورد بحث قرار خواهد گرفت. در این بین با نمودارهایی کار خواهیم کرد که مربوط به تعداد وظایف CPU برحسب زمان در یک سیستم رایانه‌ای است. تصویر زیر این تغییرات را در نمودار مربوطه نشان داده است. فرض کنید محور افقی زمان برحسب ثانیه است و محور عمودی نیز تعداد عملیات (Task) را نشان می‌دهد.

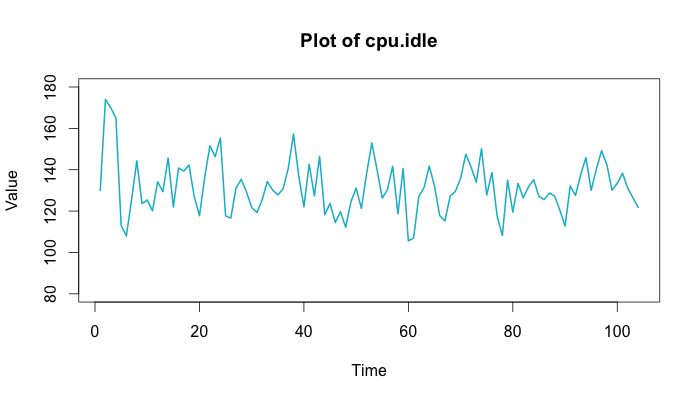
با توجه به این نمودار، مشخص است که تعداد وظیفه‌هایی که CPU در زمان انجام می‌دهد، دارای نوسانات زیادی است ولی در کل به نظر می‌رسد که حول یک مقدار ثابت (مثلا میانگین با مقدار ۱۳۰) تغییرات پایدار هستند. به چنین داده‌ها و فرآیند سری زمانی، ایستا (Stationary) می‌گویند. به این ترتیب اگر بخواهیم مقداری را برای آینده تعداد وظایف پیش‌بینی کنیم، باید مقداری حدود ۱۳۰ باشد. البته ممکن است مقدار ۱۳۰، پیش‌بینی خیلی خوبی نباشد ولی به راحتی و سادگی بدست آمده است و البته پیش‌بینی چندان بدی هم نیست.

هموارسازی نمایی در سری زمانی با میانگین متحرک

منظور از «هموارسازی نمایی» (Exponential Smoothing)، استفاده از عملگر میانگین متحرک (Moving Average) با وزن‌هایی است که به صورت نمایی از نقطه شروع کاهش پیدا می‌کنند. چنین شیوه هموارسازی را «هموارسازی نمایی سری زمانی میانگین متحرک» (Exponentially Weighted Moving Average) یا EWMA می‌نامند.

فیلم آموزش شبکه های مخابراتی (رایگان) در فرادرس

کلیک کنید

فرض کنید روی سری زمانی $$x_t$$ هموارسازی صورت گرفته و یک سری زمانی جدید با نام $$s_t$$ ساخته شده است. شیوه هموارسازی میانگین متحرک نمایی، در این حالت به شکل زیر بیان شده است.

$$\large s_t=\alpha x_t+(1-\alpha)s_{t-1}$$

رابطه ۱

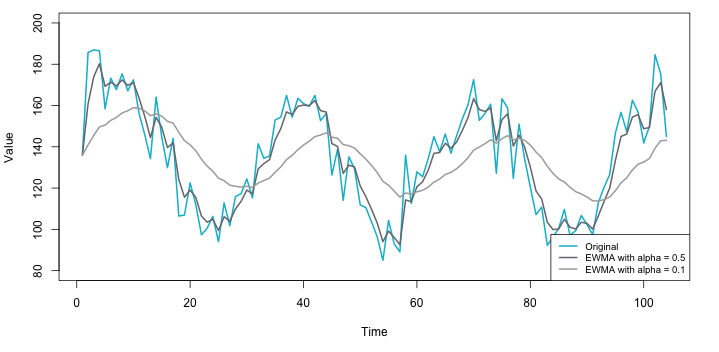
در نتیجه به نظر می‌رسد که هموارسازی روی داده مربوط به زمان $$t$$، حاصل میانگین وزنی $$x_t$$ و $$s_{t-1}$$ است که با وزن‌های $$\alpha$$ و $$1-\alpha$$ انجام شده است. تصویر زیر نتیجه این هموارسازی را به ازاء $$\alpha=0.5$$ و $$\alpha=0.05$$ نشان می‌دهد.

مشخص است که با در نظر گرفتن $$\alpha=0.5$$ منحنی خیلی هموار به نظر نمی‌رسد، زیرا سهم $$x_t$$، با نوسانات زیاد، با سهم داده‌های هموار شده زمان قبل $$s_{t-1}$$ در مدل برابر است. ولی زمانی که $$\alpha=0.05$$ است، هموارسازی بیشتر صورت گرفته و سهم مقادیر $$s_{t-1}$$ در میانگین‌گیری بیشتر است.

نکته: از آنجایی که صحبت از میانگین وزنی می‌کنیم، مشخص است که وزن‌ها باید در بازه $$(0,1)$$ باشند. از طرفی جمع وزن‌ها نیز برای نقاط با واحد (یک) برابر است.

فرض کنید قرار است براساس داده‌های سری زمانی تا زمان $$t$$ (یعنی $$x_t$$)، مقدار $$x_{t+1}$$ را پیش‌بینی کنید. اگر مقدار وزن $$\alpha$$ را در مدل ۱ کم کنید، نقش مقدار قبلی $$x_t$$ را کم کرده و در عوض نقش $$s_{t}$$ را افزایش داده‌اید. همانطور که در نمودار بالا نیز دیده شد، در مجموع، هموارسازی می‌تواند پیش‌بینی ساده و نسبتا مناسبی ارائه کند. در نتیجه $$s_t$$ برآوردگر $$x_t$$ خواهد بود.

انتخاب مقدار وزن ($$\alpha$$) در هموارسازی نمایی سری زمانی

فرض کنید که در یک سری زمانی می‌خواهیم میانگین متحرک با وزن یکسان برای همه مشاهدات داشته باشیم. اگر میانگین متحرک براساس $$n$$‌ مشاهده، بدست آید، متوسط طول عمر هر مشاهده در محاسبه میانگین متحرک چقدر است؟

با کمی دقت متوجه خواهید شد که این طول عمر برابر با حدودا $$\dfrac{n+1}{2}$$ است. به تصویر زیر دقت کنید.

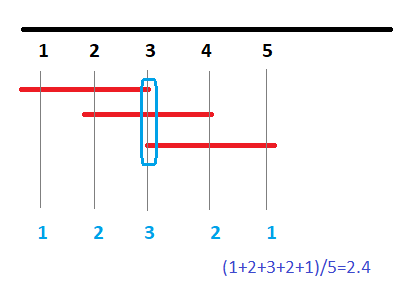
در اینجا ۵ نقطه در نظر گرفته شده و میانگین متحرک براساس سه مشاهده صورت گرفته. در نتیجه متوسط عمر نقاط برابر با $$2.6$$ است که به $$2.4$$ بسیار نزدیک است. با افزایش تعداد نمونه‌ها، به تقریب مناسبی از $$\dfrac{n+1}{2}$$ خواهیم رسید.

حال فرض کنید که می‌خواهید یک هموارسازی نمایی میانگین متحرک با وزن‌های برابر برای مشاهده ایجاد کنید. به این ترتیب کافی است که از عکس متوسط طول عمر استفاده کنید و $$\alpha=\dfrac{2}{n+1}$$ قرار بگیرد.

برای مثال فرض کنید قرار است که یک سری زمانی بر اساس نمونه‌هایی که هر ثانیه یک‌بار گرفته می‌شوند، توسط هموارسازی نمایی میانگین متحرک، پیش‌بینی شود. داده‌های مربوط به یک دقیقه جمع‌آوری شده‌اند. اگر میانگین متحرک برای زمان $$t$$ وابسته به $$t-1$$ باشد آنگاه مقدار $$\alpha$$ برابر با $$0.03278$$ خواهد بود.

$$\large \alpha= \dfrac{2}{61}= 0.032786885$$

موضوع مهم هنگام استفاده از برآورد حاصل از هموارسازی به این شکل، ایستا بودن فرآیند سری زمانی است، به این معنی که میانگین آن ثابت بوده و فرآیند دارای روند نیست. سوال مهم در اینجا این است که زمانی که نوسانات ایستا نبوده و تغییرات به صورت روند (Trend) یا فصلی (Seasonality) در سری زمانی وجود داشته باشد، به چه طریق باید عمل کرد؟

ایستایی، روند و تغییرات فصلی در هموارسازی نمایی سری زمانی

ویژگی‌های متعددی برای یک سری زمانی وجود دارد ولی در اینجا فقط به سه خاصیت اصلی یعنی ایستایی، روند و تغییرات فصلی اشاره خواهیم داشت.

• ایستایی (Stationary): به ثابت بودن میانگین تغییرات یک سری زمانی، ایستایی می‌گویند. به این ترتیب روند صعودی یا نزولی در نمودار ترسیم شده یک سری زمانی وجود نداشته و به نظر می‌رسد که تغییرات در داده‌های سری زمانی به صورت تصادفی و حول یک نقطه رخ می‌دهد. معمولا در بررسی چنین سری زمانی، از هموارسازی «میانگین متحرک وزنی نمایی» (EWMA) استفاده می‌شود.
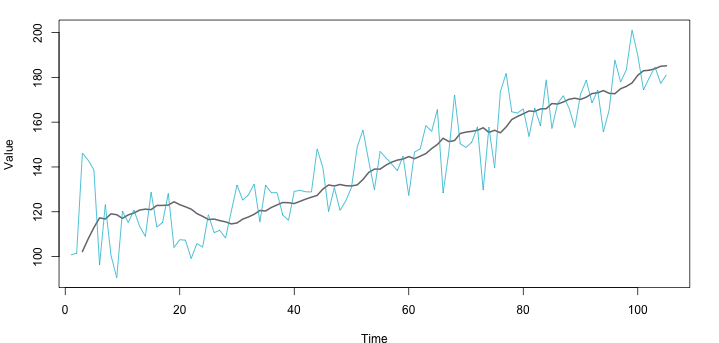
• روند (Trend): به تغییرات طولانی مدت در یک سری زمانی که طبق یک الگوی مشخص ظاهر می‌شود، روند گفته می‌شود. برای مثال روند صعودی یا نزولی نشان می‌دهد که مقدارهای مربوط به یک سری زمانی در کل افزایش دارند یا رو به کاهش هستند. معمولا تغییرات کلی که توسط روند مشخص می‌شود، به صورت معادله یا رابطه یک خط راست است. در تصویر زیر یک سری زمانی با روند صعودی را مشاهده می‌کنید.

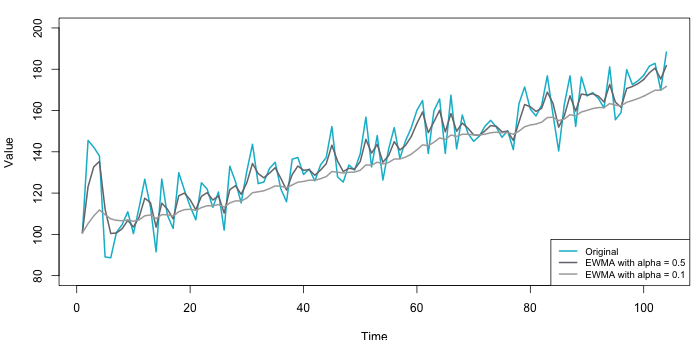
نکته: اگر روند به صورت درجه ۲ باشد، هموارسازی به شکل یک مخروط خواهد بود. در زیر، مدل هموارسازی نمایی دیده می‌شود که با سه پارامتر $$\alpha, \beta , \gamma$$ مشخص شده است.

$$\large s_t=\alpha\dfrac{x_t}{g_{t-L}}+(1-\alpha)(s_{t-1}+b_{t-1})\\ \large b_t=\beta(s_t-s_{t-1})+(1-\beta)b_{t-1})\\ \large g_t=\gamma\dfrac{x_t}{s_t}+(1-\gamma)g_{t-L}$$

رابطه ۲

• تغییرات فصلی: گاهی تغییرات تناوبی در سری زمانی، مرتبط با تغییرات فصلی است. به این معنی که تقریبا در مقاطع مشخصی از زمان، رفتار سری زمانی تکرار می‌شود. به عنوان یک مثال مناسب می‌توان به تغییرات دمایی در طول سال‌ها اشاره کرد که به صورت تناوبی تغییر می‌کند.

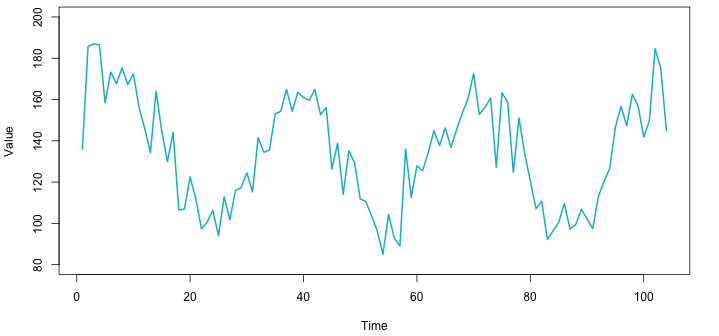
نتیجه اعمال هموارسازی نمایی سری زمانی (میانگین متحرک وزنی نمایی) روی این گونه سری‌های زمانی در تصویر زیر دیده می‌شود.

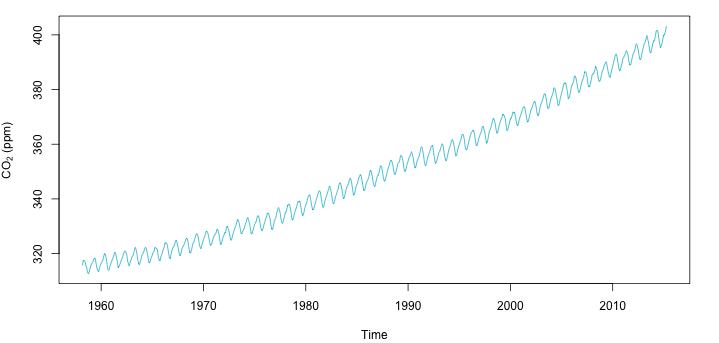
ممکن است در یک سری زمانی، هم اثر تغییرات فصلی (تناوبی) و هم روند دیده شود. در تصویر زیر تغییرات میزان گازکربنیک در اتمسفر در سال‌های مختلف ترسیم شده که نشان می‌دهد روند و تغییرات فصلی در سری زمانی تاثیرگذار هستند و از طرفی یک روند افزایشی سریع، در سال‌های ۱۹۸۰ به بعد رخ داده است.

هموارسازی نمایی سری زمانی مضاعف و درجه سه

در سال ۱۹۵۰، چارلز هولت (Charles Holt) متوجه شد که مدل هموارسازی نمایی، برای مدل‌بندی سری‌های زمانی همراه با روند، دچار مشکل می‌شود. او مدل هموارسازی نمایی ساده (طبق رابطه ۱) را تغییر داد و نتیجه کار او به نام روش هموارسازی هولت معروف شد. در روش هموارسازی هولت، دوبار هموارسازی صورت می‌گیرد. در گام اول هموارسازی براساس مقدار واقعی سری زمانی است و در گام بعدی نتایج هموارسازی، دوباره هموار می‌شوند.

$$\large s_t=\alpha x_t+(1-\alpha)(s_{t-1}+b_t)\\ \large b_t=\beta(s_t-s_{t-1})+(1-\beta)b_{t-1}$$

رابطه ۳

البته برای محاسبه مقدار پیش‌بینی طبق این الگو، باید احتیاط کرد. همانطور که دیده می‌شود در هر مرحله، یک رابطه خطی بین مقدار هموار شده در زمان $$t$$ و $$t-1$$ ایجاد شده است که $$\beta$$ شیب این خط است که باید در محاسبات پیش‌بینی به کار رود. فرض کنید که می‌خواهید مقدار سری زمانی را برای $$m$$‌ واحد زمانی بعد از $$t$$ بدست آورید. به این ترتیب می‌نویسیم:

$$\large F_{t+m}=s_t+mb_t$$

رابطه 4

همانطور که مشخص است رابطه ۴، معادله یک خط راست است، که براساس رابطه ۳ ساخته می‌شود.

نکته: اگر بخواهید مقدار سری زمانی را در زمان $$t+1$$ مشخص کنید، کافی است مقدار $$m$$ را ۱ انتخاب کنید.

زمانی که علاوه بر روند، تغییرات فصلی نیز در داده‌های سری زمانی وجود داشته باشد، استفاده از هموارسازی نمایی در سری زمانی مرتبه ۳، مناسب است. پیتر وینترز (Peter Winters) که دانشجوی هولت بود، روش استادش را گسترش داد و مدل دیگری را برای هموارسازی توسعه داد. او با دخالت دادن عامل تغییرات فصلی مدل جدیدی معرفی کرد که براساس پارامتر $$L$$‌ که وابسته به تغییرات فصلی است، هموارسازی را انجام می‌دهد.

به این ترتیب مدل پیش‌گو برای مقدار سری زمانی در فاصله $$m$$ از زمان $$t$$ به شکل زیر خواهد بود.

$$\large F_{t+m} = (s_t+mb_t)g_{t-L+m}$$

رابطه ۵

مقدار $$g_{t-L+m}$$ و $$b_t$$ باید براساس رابطه ۲ صورت گیرد.

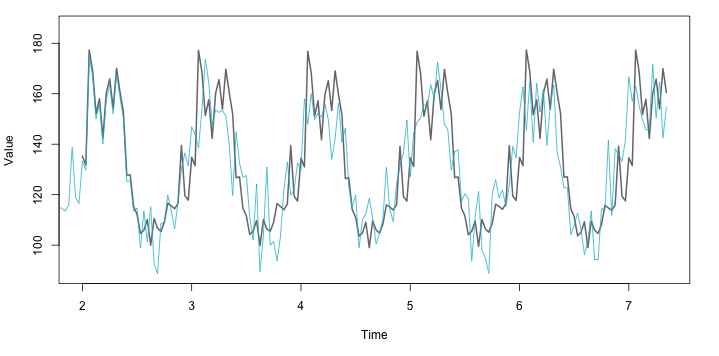
نمونه هموارسازی و پیش‌بینی سری زمانی، توسط روش هموارسازی نمایی مرتبه ۳ در تصویر ۸ دیده می‌شود. همانطور که مشخص است این مدل به خوبی از عهده پیش‌بینی مقادیر قبلی برآمده و مدلی قابل اعتماد برای داده‌های سری زمانی با روند و تغییرات فصلی به نظر می‌رسد.

هموارسازی نمایی در سری زمانی برای از بین بردن اثر داده‌های دورافتاده

زمانی که با داده‌های جریانی (Streaming Data) مواجه هستیم، باید به سرعت،‌ مشاهدات پرت (Outlier) یا نامتعارف (Abnormal) شناسایی شده و کنار گذاشته شوند.

متاسفانه ذات داده‌های جریانی، این امکان را برای شناسایی داده‌های پرت فراهم نمی‌کند در نتیجه باید نقش آن‌ها را در پیش‌بینی‌ها کاهش دهیم. راه مناسب برای بررسی داده‌های جریان و حذف اثر داده‌های نامتعارف، استفاده از هموارسازی است، بخصوص که هموارسازی نمایی میانگین متحرک با توجه به وزن‌دهی به مشاهدات، این کار را به بهترین وجهی انجام می‌دهد. پیاده‌سازی الگوریتم و نحوه محاسبات برای هموارسازی نمایی میانگین متحرک برای داده‌های ساختگی توسط کدهای زیر که با زبان Go‌ نوشته شده‌اند، صورت پذیرفته است.

همچنین برای آزمایش این کدها و عملکرد آن‌ها روی یک مجموعه داده فرضی بهتر است برنامه زیر را اجرا کنید.

خلاصه و جمع‌بندی

تشخیص ناهنجاری‌ها و مقابله با آن در زمان واقعی (Real Time) یکی از مشکلاتی است که در پیش‌بینی‌ها باید مورد بررسی قرار گیرد. زیرا در سری زمانی نمی‌دانید در آینده چه داده‌ای ظاهر خواهد شد و همیشه براساس گذشته فرآیند تصادفی مدل را ساخته‌اید.

به همین دلیل پیش‌بینی و مدل‌سازی براساس داده‌های سری زمانی می‌تواند واقعاً پیچیده باشد، اما بسیاری از تکنیک‌ها و روش‌های ساده و کارآمد مانند EWMA یا (Exponentially Weighted Moving Average) با اضافه کردن کمی زمان و هزینه، می‌توانند بهترین نتیجه را بوجود آورند.

البته استفاده از  تکنیک‌های پیچیده‌تر برای موارد بسیار خاص مناسب بوده و پیش‌بینی را با دقت بیشتری انجام می‌دهند ولی به پیچیدگی مدل و هزینه‌های محاسباتی نیز می‌افزایند. در این نوشتار با هموارسازی هولت وینترز آشنا شدیم و براساس نمودارها و روابطی که معرفی کردیم، ساختار آن را آموزش دادیم.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب سری زمانی هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های پیش‌‌ بینی و تحلیل سری‌‌ های زمانی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده
• سری زمانی در علم داده — از صفر تا صد
• تابع خودهمبستگی (Autocorrelation Function) — مفاهیم و کاربردها

^^