سری زمانی در SPSS — راهنمای کاربردی
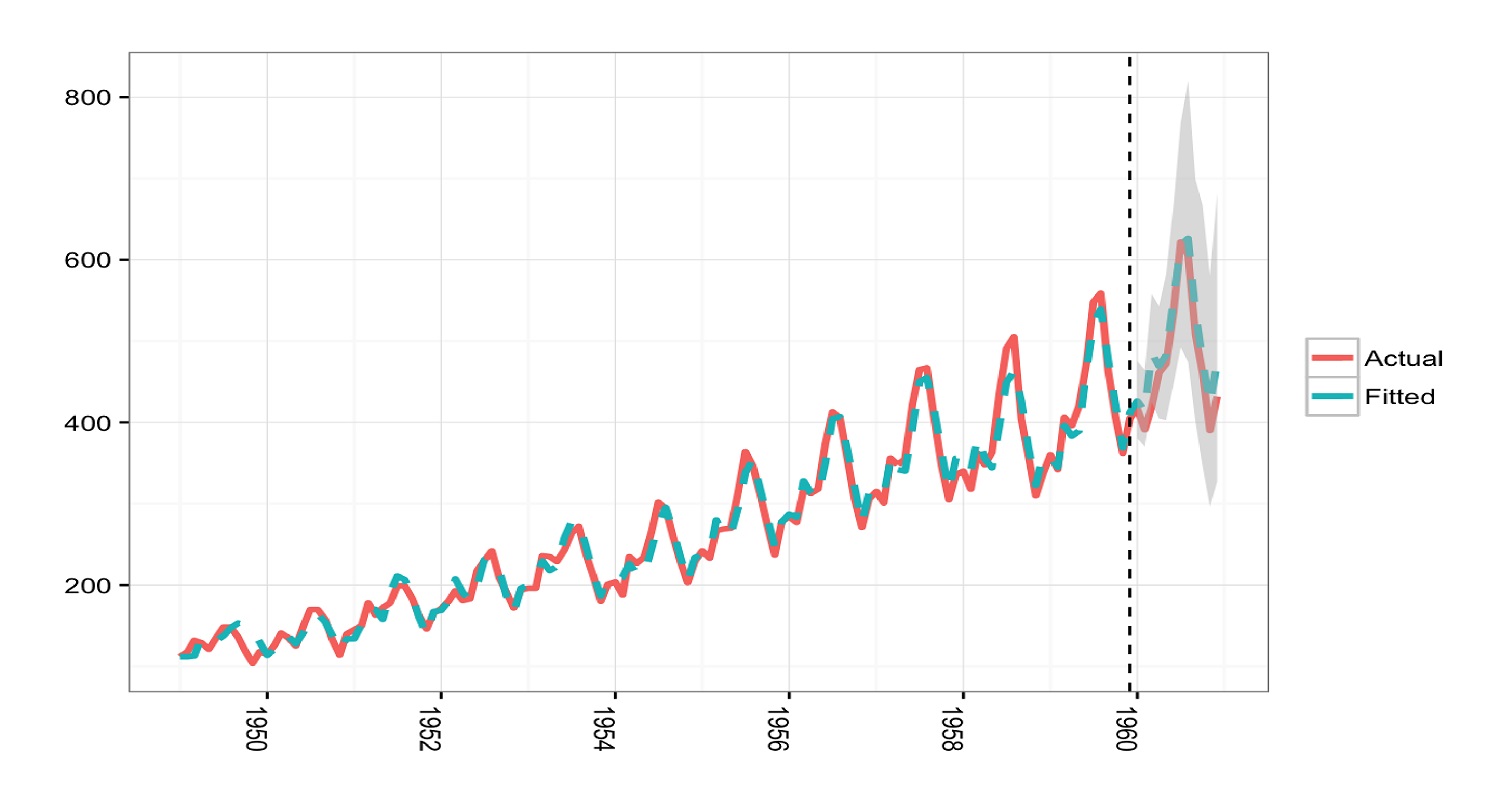
دادههای وابسته به زمان، رفتار متفاوتی با دادههای انواع دیگر تحلیلهای آماری دارند. در سریهای زمانی (Time Series)، مشاهدات با یکدیگر وابستگی داشته در حالیکه در تحلیلهای دیگر مانند تحلیل و آزمون فرض میانگین، شرط مستقل و تصادفی بودن مشاهدات از شرطهای اولیه انجام چنین تحلیلهایی محسوب میشوند. تحلیل سری زمانی در SPSS به علت اینکه محاسبات به راحتی و با نمودارهای گویا صورت میگیرد در بین کاربران از محبوبیت خاصی برخوردار است. بنابراین در این نوشتار به بررسی تحلیلهای سری زمانی در SPSS میپردازیم و در این بین از پرونده اطلاعاتی میزان تولید غله در آمریکا استفاده میکنیم که از طریق (+) قابل دسترسی است. به این ترتیب با ورود این دادهها، کار تحلیل سری زمانی در SPSS را مرور و مورد بررسی قرار میدهیم.
از کاربردهای مهم تحلیل سریهای زمانی میتوان به پیشبینی (Forecasting) رفتار پدیدههای تصادفی مرتبط با زمان اشاره کرد و بوسیله مدلبندی و بررسی سازگاری دادهها با یکی از مدلهای مختلف سری زمانی، قادر به تعیین مقدارهای آتی پدیده تصادفی خواهیم بود.
برای آشنایی بیشتر با روشها و مدلهای تحلیل سری زمانی بهتر است مطلب تحلیل سری زمانی — تعریف و مفاهیم اولیه را مطالعه کنید. همچنین خواندن نوشتارهای دنبالهای تحلیل سری زمانی با پایتون — مقدمات و مفاهیم اولیه، تحلیل سری زمانی با پایتون — معرفی انواع مدل ها و تحلیل سری زمانی با پایتون — مدل های ترکیبی و پیچیده نیز خالی از لطف نیست.
سری زمانی در SPSS
در دیگر نوشتارهای فرادرس با مفاهیم اولیه سریهای زمانی و نحوه مدلبندی دادههای وابسته به زمان صحبت کردیم. ولی در این نوشتار سعی داریم که به نحوه انجام این تحلیلها به کمک یک نرمافزار کاربردی آشنا شویم. سری زمانی در SPSS ساده است و احتیاج به دستورات متعدد ندارد، بلکه بیشتر تحلیلهای اولیه را SPSS به طور خودکار انجام داده و نتایج را به ما نشان میدهد.
البته برای تعیین دقت و کارایی مدل ارائه شده توسط نرمافزار باید، ارزیابیهایی نیز توسط کاربر انجام شود که در ادامه به آنها نیز خواهیم پرداخت.
مدلهای سری زمانی در SPSS
از شیوه و مدلهای مختلفی برای تعیین ساختار دادههای حاصل از یک پدیده وابسته به زمان استفاده میشود. یکی از کاملترین مدلها را میتوان مدل ARIMA در نظر گرفت که اغلب به آن مدل «خودهمبسته یکپارچه میانگین متحرک» (Autoergressive Integrated Moving Average) میگویند.
چنین مدلی از سه بخش تشکیل شده است. بخش اول همانطور که از نامش پیداست، خودهمبسته (Autoregressive) بودن دادهها را مشخص و مدلبندی میکند. بخش دوم نیز یکپارچگی (Integrated) و بخش سوم نیز میانگین متحرک (Moving Average) است که برای هموارسازی مقادیر سریزمانی به کار میرود. ترکیب این مدلها، منجر به وجود مدلی کامل و توانا خواهد شد. در این نوشتار چنین مدلی را برای تحلیل سری زمانی دادههای رشد گیاه جو دو سر ( Oats Yield per Acre) در آمریکا از سال ۱۸۷۶ تا ۲۰۱۵ مورد استفاده قرار میدهیم. این دادهها سالانه تهیه شده و از اینجا (+) قابل دریافت است.
میزان برداشت جو دو سر از حدود نیمهکتار از مزارع آمریکا در سالهای یاد شده، اندازهگیری شده و به عنوان یک متغیر پیوسته در نظر گرفته میشود. این مقادیر در طول ۱۴۰ سال ثبت شدهاند در نتیجه به نظر میرسد تعداد مشاهدات برای تشکیل یک مدل سریزمانی مناسب باشد. خوشبختانه در هیچ سالی نیز داده مشاهده نشده (Missing) وجود ندارد.
مراحل انجام یک سری زمانی در SPSS
یک مدل سریزمانی ARIMA دارای پارامترهای مختلفی است که باید شناسایی شده و توسط دادهها برآورد شوند. این پارامترها که به ترتیب آنها را با p برای مدل خودهمبستگی (AR)، پارامتر d یا درجه تفاضلی (بخش یکپارچگی) برای مدل Integrated، پارامتر q برای مدل میانگین متحرک (Moving Average) نشان میدهند، مشخصههای اصلی مدل ARIMA محسوب میشوند. چنین مدلی براساس این پارامترها به صورت زیر نمایش داده میشود.
$$\large ARIMA(p,d,q)$$
مدل اتورگرسیو میانگین متحرک به بیان ریاضی به صورت زیر نوشته میشود.
$$\large x_t=a_1x_{t-1}+a_2x_{t-2}+\cdots +a_{p}x_{t-p}+w_t+b_1w_{t-1}+\cdots+b_qw_{t-q}$$
این رابطه را به شکل سادهتری نیز میتوان نشان داد. کافی است از نماد جمع در رابطه استفاده کنیم.
$$\large x_t=\sum_{i=1}^p a_ix_{t-i}+w_t+\sum_{i=1}^qb_iw_{t-i}$$
واضح است که تفاضلگیری به منظور ایستایی (Stationary) مدل در ARIMA به کار میرود. هدف در اینجا برآورد پارامترهای $$a_i$$ و $$b_i$$ است که به کمک شناسایی $$p$$، $$d$$ و $$q$$ صورت میگیرد که به آنها مرتبه یا درجههای مدل میگویند.
ابزار مناسب برای تشخیص مرتبههای مدل، رسم نمودار ACF یا تابع خود همبستگی (Autocorrelation Function) و PACF یا خودهمبستگی جزئی (Partial Autocorrelation Function) و مطابقت آنها با الگویهای اصلی مدل ARIMA است. به این منظور دستورات زیر را اجرا میکنیم.
از فهرست Analysis گزینه Forecasting و دستور Autocorrelations را انتخاب میکنیم. متغیر Oats Yield per Acre را به عنوان متغیر مورد تحلیل در کادر Variables قرار میدهیم. برای رسم نمودارهای مربوطه نیز کافی است در قسمت Display گزینههای Autocorrelations و Partial autocorrelations را انتخاب کنیم.
با انجام این کار، خروجیها به صورت زیر در خواهند آمد. ضریب همبستگی سریالی براساس تاخیرهای (Lags) مختلف در این نمودارها قابل مشاهده است.
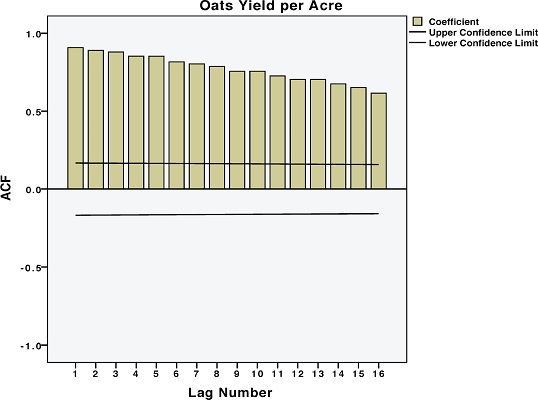
از آنجایی که همبستگیهای سریالی (خود همبستگیها) برای مشاهدات به سمت صفر میل نمیکند، شرط ایستایی (Stationary) سری زمانی زیر سوال میرود. بنابراین باید بوسیله تفاضلگیری (Difference) مدل را ایستا کرد. برای این کار کافی است که در پنجره Autocorrelations گزینه Difference را با مرتبه ۱ فعال کنید. نمودار بعدی نتیجه ایستا کردن دادهها را در نمودار تابع خودهمبستگی (ACF) نشان میدهد.
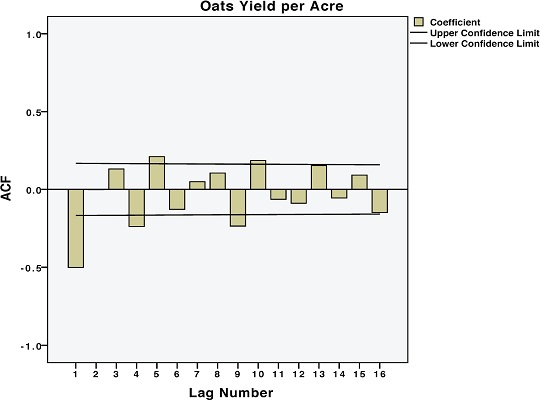
این نمودار نیز در تاخیر (Lag) اول، میزان همبستگی منفی بزرگی را نشان میدهد که البته با افزایش تاخیرها، به صفر میرسد. مشخص است که روند تابع ضریب همبستگی سریالی، نزولی است و به سمت صفر میل میکند. در نتیجه مدل در این حالت ایستایی، براساس تفاضلگیری مرتبه اول داشته است، بنابراین بهتر است که پارامتر یکپارچهسازی (Integrated) را به صورت $$d=1$$ در نظر بگیریم.
حال بهتر است نگاهی هم به نمودار تابع ضریب همبستگی جزئی بیاندازیم.
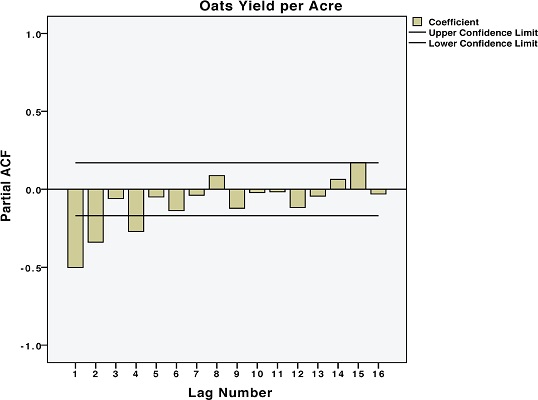
براساس نمودار تابع ضریب خودهمبستگی جزئی و تابع ضریب خودهمبستگی به نظر میرسد که انتخاب مدل میانگین متحرک مرتبه ۱ یعنی $$q=1$$ مناسب باشد. به این ترتیب مدل $$ARIMA(0,1,1)$$ برای ایجاد مدل سری زمانی دادهها به کار خواهد رفت. حال به دستور برآورد پارامترهای مدل ARIMA در SPSS میپردازیم.
برآورد پارامترهای مدل سری زمانی در SPSS
خوشبختانه در SPSS امکان مدلسازی دادههای سری زمانی به شکل بسیار سادهای وجود دارد. کافی است از فهرست Analysis گزینه Forecasting را باز کرده و دستور Create Traditional Model را انتخاب کنید.
پنجرهای به شکل زیر ظاهر خواهد شد.
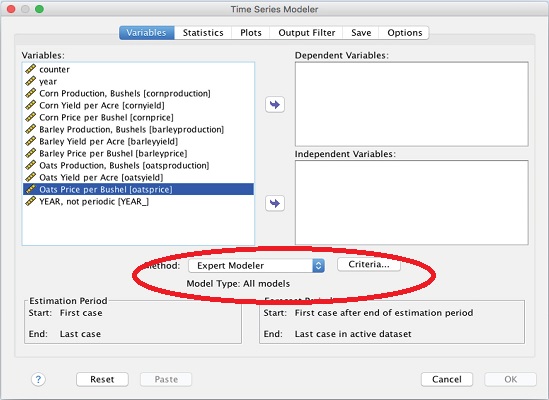
متغیر Oats Yeild per Acre که با نام oastyeild مشخص شده را در کادر سمت راست (Dependent Variables) وارد کنید. در پایین پنجره نیز شیوه مدلسازی را از حالت مدلساز هوشمند (Expert Modeler) به ARIMA تغییر دهید. این قسمت توسط یک بیضی قرمز رنگ در تصویر بالا دیده میشود.
حال لازم است با توجه به نمودارها و تحلیلهایی که قبلا انجام دادهاید، پارامترهای مدل ARIMA را مشخص کنید. برای انجام این کار دکمه Criteria را که در تصویر مشخص شده، کلیک کنید تا پارامترهای مربوط به تعیین مرتبههای مدل ARIMA ظاهر شود.
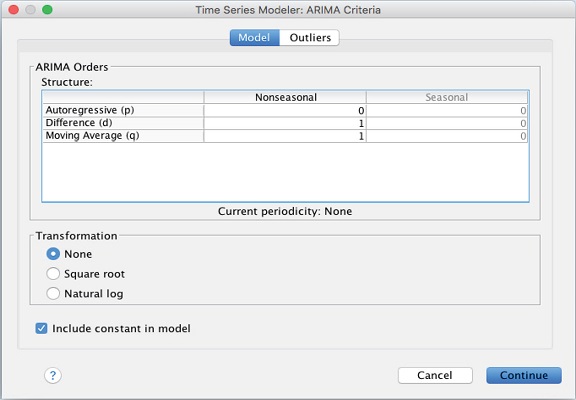
هر یک از مقادیر مربوط به مرتبههای $$p$$، $$d$$ و $$q$$ را مطابق با تصویر بالا تنظیم کنید و دکمه Continue را بزنید. با این کار به پنجره اولیه بازگشته و نام مدل و درجه یا رتبههای مدل مطابق با آنچه تنظیم کردهاید، ظاهر خواهد شد.
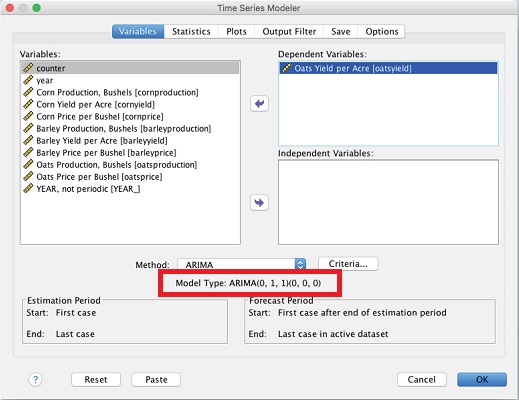
اگر میخواهید، هنگام محاسبات مربوط به مدل سری زمانی در SPSS، آمارههای دلخواهتان نمایش داده شود، از برگه Statistics استفاده کنید. در این میان شاخصهایی مانند Stationary R Square و مربع ضریب همبستگی R به همراه مقادیر برازششده آماره Ljung-Box و مشاهدات دورافتاده نیز مفید هستند.
برای ارزیابی مدل ساخته شده نیز نمایش نمودارهای تابع خودهمبستگی باقیماندهها (خطا) که به Residual autocorrelation function معروف است ضروری است. همچنین مشاهده نمودار تابع خودهمبستگی جزئی نیز ما را در ارزیابی صحیح همراهی میکند.
با تکمیل این پنجرهها و اجرای دستور سری زمانی، خروجی سری زمانی در SPSS برای مجموعه دادههای مورد نظر مطابق با تصویر زیر در جدول و نمودارها، ظاهر میشود.
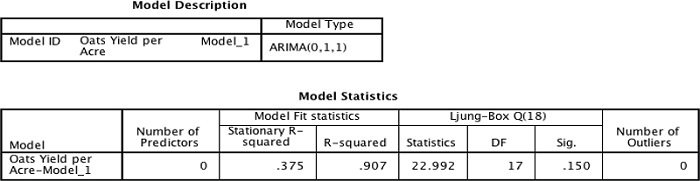
در ابتدا، جدولی به عنوان معرفی مدل برازش شده دیده میشود. سپس آمارههای درخواست شده ظاهر میشوند. همانطور که دیده میشود، ضریب همبستگی بین مشاهدات و مقادیر برازش شده که در R-Squared دیده میشود، بزرگ بوده و خبر از برازش مناسب دادهها میدهد. همچنین براساس آماره Q با مقدار احتمال $$0.150$$ فرض صفر که تصادفی بودن فرآیند را مشخص میکند، رد نمیشود. به این ترتیب از آنجایی که مدل را بدون خودهمبستگی در نظر گرفتیم، به نظر میرسد که مدل مناسبی را پیدا کردهایم. در نمودارهایی که در ادامه ایجاد شدهاند، این شرایط برای باقیماندهها نیز مورد بررسی قرار گرفتهاند. فرض بر این است که باقیماندهها مستقل از یکدیگر بوده و تصادفی هستند. برای نمایش این وضعیت نمودارهای ACF و PACF برای باقیماندهها کمک گرفته شده است.
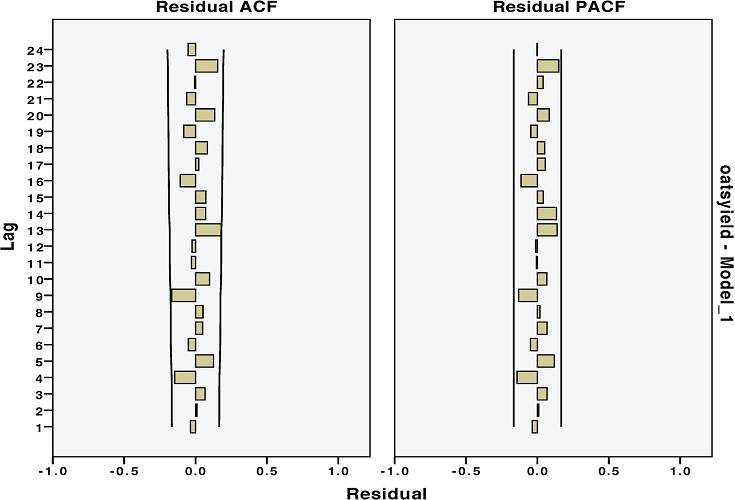
همانطور که دیده میشود این ضرایب همبستگی مقدار کوچکی داشته و بدون یک روند، خودهمبستگی بین باقیماندهها در تاخیرهای مختلف تغییر میکند. بنابراین ارزیابی مدل، آن را مناسب تشخیص میدهد.
جمعبندی و خلاصه
در این نوشتار با سریزمانی ARIMA آشنا شده و شیوه پیادهسازی آن را برای دادههای واقعی توسط SPSS فرا گرفتیم. همچنین برای ارزیابی مدل، از نمودار و شاخصهای آماری استفاده کرده و مدل مناسبی برای مجموعه دادههای واقعی میزان محصول جو دوسر در آمریکا ارائه شد. در انتها نیز به کمک بررسی باقیمانده (خطا) مدل، تایید شد که مدل بدست آمده برای توصیف پدیده تصادفی وابسته به زمان (سری زمانی) مناسب است.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای پیش بینی و تحلیل سری های زمانی
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای SPSS
- ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده
- سری زمانی در علم داده — از صفر تا صد
- تابع خودهمبستگی (Autocorrelation Function) — مفاهیم و کاربردها
^^











با سلام و وقت بخیر
اگر در این مدل missing data داشته باشیم چه کاری باید انجام دهیم؟؟
درود به شما خواننده گرامی؛
معمولا هنگامی که با دادههای گمشده در یک تحلیل آماری مواجه میشویم، به دو شیوه میتوان عمل کرد. یا مشاهده مورد نظر را نادیده گرفت. یا برای مقدار گمشده یک جایگزین انتخاب یا محاسبه کرد.
برای آشنایی بیشتر با نحوه رفتار با داده های گمشده و همچنین انواع آنها، به نوشتارهای داده گمشده یا ناموجود (Missing Data) در R – روش های پاکسازی داده ها یا داده های گمشده در SPSS — راهنمای کاربردی مراجعه کنید.
با آرزوی تندرست و بهروزی
سلام اقای دکتر عذر میخام اگه بخوام سری زمانی بدون تاخیر.با تاo خیر یک ماهه و تاخیر چندماهه داشته باشم چکار باید بکنم .ممنون میشم به ایمیلم پاسخ بدین
سلام و درود
از اینکه با مجله فرادرس همراه هستید بسیار خرسندیم!
در سری زمانی، تشخیص الگوها و مدلهای امری ضروری است. برای این که متوجه بشوید که تاخیرات (Lag) در مدل شما به چه میزان است، ترسیم نمودارهای ACF و PACF لازم است. برمبنای این که رفتار این گونه نمودارها چگونه است، میزان تاخیر در مدل مشخص میشود. پس در حقیقت تشخیص تاخیر زمانی در دادهها و مدل میانگین متحرک برمبنای نمودارها تعیین میشود. منظور از تاخیر نحوه میانگین گیری در مدل میانگین متحرک است که میخواهید از هر چند مشاهده میانگینگیری صورت بگیرد. پس ربطی به تاخیر ثبت دادهها ندارد. ممکن است دادهها در تاریخهای نامخشصی ثبت شده باشند ولی شما به یک مدل با تاخیر (Lag=۲) برسید.
باز هم از اینکه مطالب فرادرس را دنبال می کنید سپاسگزاریم.
از فرادرس بعیده همچین آموزش ناقص و گنگی
اصلا مشخص نیست داده ها چی هست سالانه اس ماهانه اس فصلیه؟؟
سلام و سپاس از توجه شما به مطالب فرادرس
دادههای مربوط به این نوشتار به صورت سالانه تهیه شده است. نحوه دریافت این دادهها در متن مورد اشاره قرار گرفته است.!
با تشکر از همراهی شما با مجموعه مجله فرادرس