نیروهای غیرموازی در استاتیک — به زبان ساده
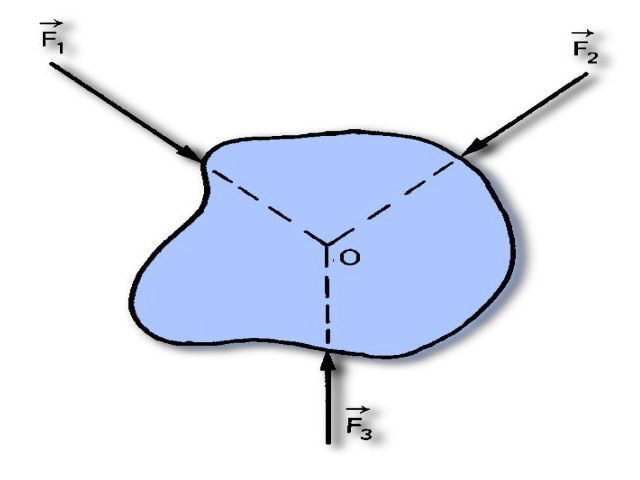
در مطالب گذشته وبلاگ فرادرس در مورد مفاهیم مربوط به استاتیک، گشتاور و نیرو بحث شد. از این رو در این مطلب قصد داریم تا نیروهای غیرموازی را در یک سیستم معرفی کرده و نحوه بدست آوردن تعادل آنها را با استفاده از چند مثال توضیح دهیم.
نیروهای غیرموازی
همانطور که در مطلب استاتیک نیز توضیح داده شد، به منظور بدست آوردن اندازه نیروهای موجود در یک سیستم ایستای دوبعدی، سه معادله باید حل شوند. این سه معادله شامل تعادل در راستاهای $$ x , y $$ و تعادل گشتاوری در راستای عمود به صفحه است.
این معادلات را میتوان به صورت زیر بیان کرد:
$$ \large \Sigma F _ x = 0 \ \mathbf { o r } \ \Sigma F _ H = 0 $$
$$ \large \Sigma F _ y = 0 \ \mathbf { o r } \ \Sigma F _ V = 0 $$
$$ \large \Sigma M _ O = 0 $$
بدیهی است که روابط فوق تا $$ 3 $$ مجهول را حل میکنند. در حالتی که سیستم بیش از $$ 3 $$ مجهول داشته باشد، تحت عنوان نامعین استاتیکی شناخته میشود. سازههای نامعین در مقوله استاتیک قرار نگرفته و در مطالب مربوط به مقاومت مصالح مورد بررسی قرار میگیرند. در آینده و در مطلبی جداگانه این نوع از سیستمها را نیز بررسی خواهیم کرد.
مثال ۱
خرپایی را مطابق با شکل زیر در نظر بگیرید. با توجه به نیروهای وارد شده به این خرپا، عکسالعملهای وارد شده به آن در نقاط $$ A $$ و $$ B $$ را بیابید.
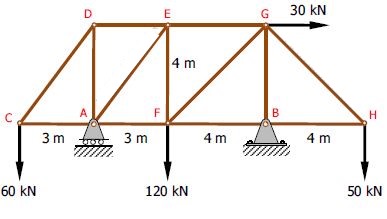
در حل مسائل استاتیک نحوه انتخاب سیستم در سرعت رسیدن به پاسخ بسیار موثر است. توجه داشته باشید که تکیهگاهِ $$ A $$ به صورت غلتکی است؛ بنابراین نیرویی افقی در آن وجود ندارد. در نتیجه برای بدست آوردن عکسالعمل در تکیهگاه $$ A $$، در اولین گام حول نقطه $$ B $$ گشتاورگیری کرده و به این صورت نیرو در این تکیهگاه به صورت زیر بدست خواهد آمد.
$$ \large \begin {gather*} Σ M _ B = 0 \\\\
7 R _ A + 4 ( 30 ) + 4 ( 50 ) = 10 ( 60 ) +4 ( 120 ) \\\\
R _ A = 108.57 k N \end {gather*} $$
بر خلاف $$ A $$ در تکیهگاه $$ B $$ هم نیروی افقی و هم نیروی عمودی وجود دارد. به منظور بدست آوردن عکسالعمل عمودی، کافی است حول نقطه $$ A $$ گشتاورگیری کرده، عکسالعمل عمودی در این نقطه برابر با مقدار زیر بدست خواهد آمد.
$$ \large \begin {gather*} Σ M _ A = 0 \\ \\
7 B _ V + 3 ( 60 ) = 3 ( 120 ) + 4 ( 30 ) + 11 ( 50 ) \\ \\
B _ V = 121.43 k N \end {gather*} $$
نیروی افقی نیز با نوشتن تعادل در راستای افقی، برابر میشود با:
$$ \large \begin {gather*} Σ F _ H = 0 \\ \\
B _ H = 30 k N \end {gather*} $$
نهایتا اندازه و جهت نیرو در $$ B $$، برابر میشود با:
$$ \large \begin {gather*} R _ B = \sqrt { { B _ H } ^ 2 + { B _ V } ^ 2 } = \sqrt { 30 ^ 2 + 121.43 ^ 2 } \\ \\ \Rightarrow R _ B = 125.08 \, \text { kN} \end {gather*} $$
$$ \large \tan \theta _ { B x } = \dfrac { B _ V } { B _ H } = \dfrac {121.43} { 30 } $$
$$ \large \theta _ { B _ x } = 76.12 ^ \circ $$
بنابراین اندازه نیرو در تکیهگاه $$ B $$ برابر با $$ R _ B = 12.08 \, \text{ kN}$$، در جهت $$ 76.12 ^ \circ $$ شمال غربی است.
مثال ۲
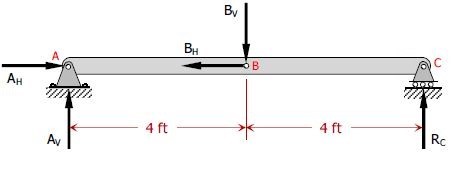
قرقرهای به قطر $$ 4 \ \ \text f \text t $$، جرمی برابر با $$ 200 \ \ \text l \text B $$ نگه داشته است. تیر نیز در وسط طولش با قرقره پین شده است. همچنین مطابق با شکل، در نقطه $$ C $$، تکیهگاه به صورت غلتک است. با صرف نظر کردن از جرم تیر، عکسالعملها را در نقاط $$ A , C $$ بدست آورید.
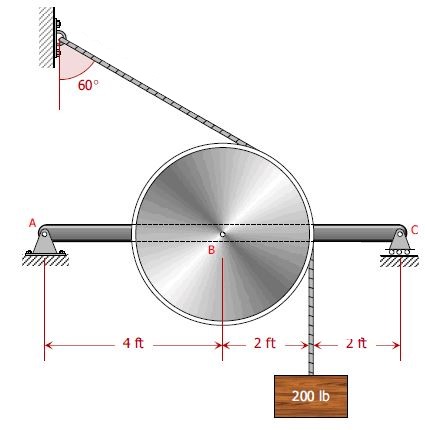
به منظور پاسخ به این سوال، باید نیروی کشش موجود در فنر را بدانیم. اندازه این نیرو برابر است با:
$$ \large T = 200 \ \ \text l \text B $$
در حقیقت این نیرو با گشتاورگیری حول نقطه $$ B $$، به دست آمده است. در ادامه نمودار آزاد قرقره نشان داده شده است.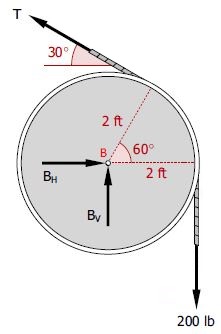
با نوشتن تعادل برای تکیهگاه $$ B $$(این تکیهگاه هم روی قرقره و هم روی تیر قرار گرفته)، نیروهای افقی و عمودی به صورت زیر بدست خواهند آمد.
$$ \\ \large \begin {gather*} Σ F _ V = 0 \\ B _ V + T \sin30 ^ ∘ = 200 \\ B _ V + 200 \sin30 ^ ∘=200 \\ B _ V=100 lb \end {gather*} $$
$$ \\ \large \begin {gather*} Σ F_ H = 0 \\ B _ H = T \cos30 ^ ∘ \\ B _ H = 200 \cos30 ^ ∘ \\ B _ H = 173.20 lb \end {gather*} $$
در مرحله بعد با رسم نمودار آزاد تیر به صورت زیر و نوشتن تعادل حول نقطه $$ A $$، اندازه نیرو در نقطه $$ C $$ برابر میشود با:
$$ \large \begin {gather*} Σ M _ A = 0 \\
8 R _ C = 4 B _ V \\
8 R _ C = 4 ( 100 ) \\
R _ C = 50 l b \end {gather*} $$
همچنین با محاسبه گشتاور حول نقطه $$ C $$، عکسالعمل افقی در تکیهگاه $$ C $$ برابر میشود با:
$$ \large \begin {align*} Σ M _ C & = 0 \\ 8 A _ V & = 4 B _ V \\ 8 A _ V & = 4 ( 100 ) \\ A _ V & = 50 l b \end {align*} $$
در مرحله بعد با نوشتن تعادل در راستای افقی، نیروی افقی نیز برابر با عدد زیر بدست میآید.
$$ \large \begin {align*} Σ F _ H & = 0 \\ A_H & = B _ H
A _ H = 173.20 lb \end {align*} $$
در نتیجه اندازه عکسالعمل در $$ A $$ برابر میشود با:
$$ \large \begin {align*} R _ A & = \sqrt { { A _ H } ^ 2 + { A _ V } ^ 2 } \\ R_A & = \sqrt{173.20^2 + 50^2} \\ R _ A & = 180.27 \, \text{ lb} \end {align*} $$
همچنین جهت این نیرو برابر است با:
$$ \large \begin {align*} \tan θ _ { A x } & = \dfrac { A _ V } { A _ H }
\\ \tan θ _ { A x } & = 50173.20 \\ \Rightarrow θ _ { A x } & = 16.1^∘ \end {align*} $$
بنابراین اندازه عکسالعمل در تکیهگاه $$ A $$ برابر با $$ R _ A = 180.27 \, \text { lb} $$ بوده که با محور افقی زاویه $$ 16.1^ \circ $$ میسازد.
در برخی از موارد میتوان با استفاده از فرضیاتی حل مسئله را آسانتر کرد. برای نمونه در نتیجه قانون سوم نیوتن میتوان گفت عکسالعمل تکیهگاه همواره به جسمی که به آن سطح نیرو وارد میکند، عمود است. در ادامه مثالی ارائه شده که با استفاده از این فرض میتوان نیروها را در سطح محاسبه کرد.
مثال ۳
مطابق با شکل زیر فرض کنید میلهای بین دو سطح شیبدار قرار گرفته است. نیروی $$ T $$ به منظور افقی ماندن تیر چقدر باید باشد.

نیرویی که به تیر در نقاط $$ A , B $$ وارد میشود، عمود است.
بنابراین در حالت کلی دو نیروی خارجیِ عمودی و دو نیرو نیز در نقاط $$ A $$ و $$ B $$ به تیر وارد میشود. بنابراین میتوان مثلث نیرویی را به صورت زیر در نظر گرفت.
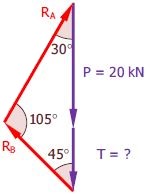
توجه داشته باشید که مثلث فوق معادل با برآیند نیروهای عمودی وارد به تیر است. از این رو میتوان از قانون سینوسها به منظور بدست آوردن رابطه بین $$ R _ A $$ و $$ T $$ به صورت زیر استفاده کرد.
$$ \large \begin {gather*} \dfrac { R _ A } { \sin 45 ^ \circ } = \dfrac { 20 + T } { \sin 105 ^ \circ } \\ R _ A = 0.732 ( 20 + T ) \\ R _ A = 14.641 + 0.732 T \end {gather*} $$
حال با گشتاورگیری حول نقطه $$ B $$ و جایگذاری رابطه فوق به جای $$ R _ A $$، اندازه $$ T $$ برابر میشود با:
$$ \large \begin {gather*} Σ M _ B = 0 \\\\
4 ( R _ A cos30 ^ ∘ ) = 3 ( 2 0 ) + 1 ( T ) \\\\
4 ( 14.641 + 0.732 T ) cos30 ^ ∘ = 60 + T \\\\
50.7179 + 2.5357 T = 60 + T \\\\
1.5 3 57 T = 9.2 8 21
\Rightarrow T = 6.04 k N \end {gather*} $$
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:










