نمونه آماری چیست؟ — به زبان ساده

برای تحلیل و شناخت رفتار یک پدیده (طبیعی یا غیرطبیعی) که برمبنای شانس یا احتمال عمل می‌کند، به داده و اطلاعات احتیاج داریم. این اطلاعات را می‌توان هم برمبنای سرشماری و با توجه به جامعه آماری، جمع‌آوری کرد یا با توسل به نمونه‌گیری، به بخشی از اطلاعات جامعه دسترسی پیدا کرده و به کمک نمونه آماری خصوصیات و ویژگی‌های جامعه را تشخیص داد. هر چند استفاده از جامعه و سرشماری نسبت به نمونه آماری اولویت دارد ولی گاهی به علت نامتناهی بودن جمعیت یا هزینه و زمان زیاد برای بررسی جامعه، دست به نمونه‌گیری می‌زنیم. در این متن به موضوع نمونه آماری و خصوصیات آن اشاره خواهیم داشت و از جنبه آماری به مسئله نمونه‌گیری می‌پردازیم.

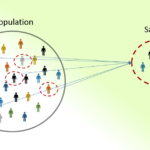
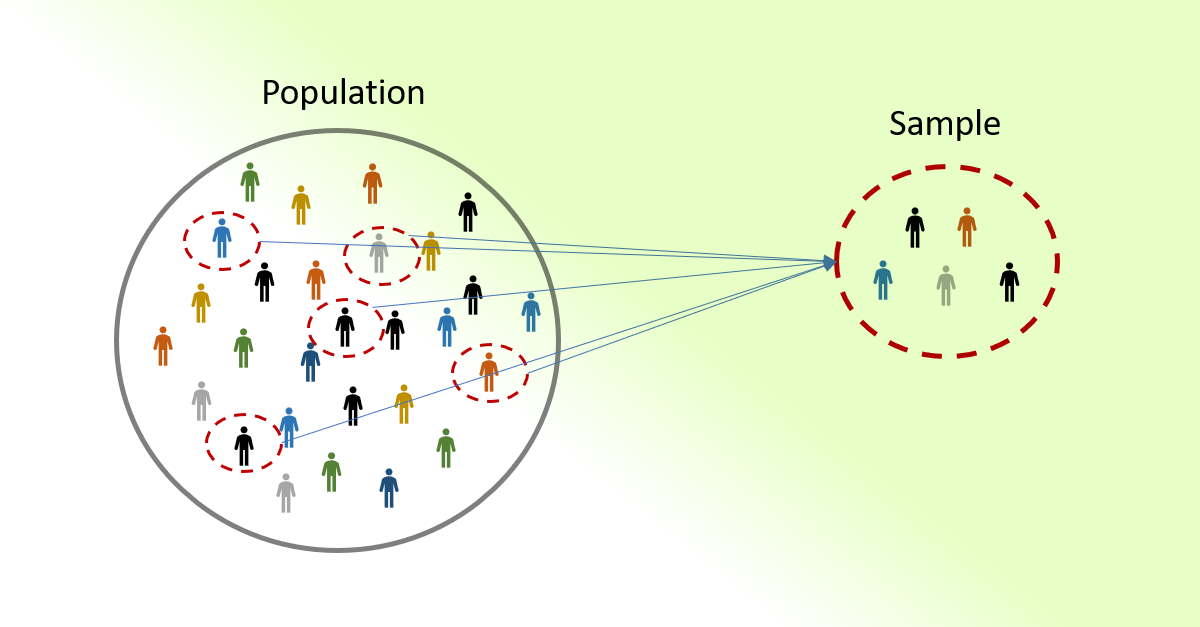
در آمار با توجه به ساختار جامعه، روش‌های مختلف نمونه‌گیری وجود دارد. برای آشنایی با این شیوه‌های تهیه نمونه، پیشنهاد می‌شود که مطالب روش‌ های نمونه‌گیری (Sampling) در آمار — به زبان ساده و تعیین حجم نمونه در تحلیل‌ های آماری — به زبان ساده را مطالعه کنید. همچنین خواندن نمونه‌گیری و بازنمونه‌گیری آماری (Sampling and Resampling) — به زبان ساده و جامعه آماری — انواع داده و مقیاس‌های آن‌ها نیز خالی از لطف نیست.

نمونه آماری

حتما ضرب المثل قدیمی،‌ «مشت نمونه خروار است» را شنیده‌اید. این عبارت به مزیت استفاده از نمونه و قابلیت‌های آن اشاره دارد. به جای اینکه خروارها از محصول (مثل گندم) را مورد بررسی قرار دهیم، یک مشت از آن‌ها را مورد بازبینی قرار داده و می‌توانیم به وضعیت کل محصول آگاه شویم. البته در این ضرب المثل، به خطای نمونه‌گیری اشاره نشده است.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

به هر حال استفاده از بخش خاصی از جامعه آماری و استنباط براساس آن روی کل جامعه،‌ همواره با خطا نیز همراه است. ممکن است نمونه گرفته شده، از قسمت خوب محصول بوده یا اینکه فروشنده بخشی از بهترین محصول را برای نمونه‌گیری در اختیار ما قرار داده است. در این حالت قضاوت ما با شک و شبه همراه بوده و به اصطلاح، «اریب» (Bias) خواهد بود. در فارسی و ادبیات آماری، گاهی به جای اریبی، عبارت «تُرُشی» یا «کج‌تابی»‌ نیز به کار می‌رود.

نکته: وجود اریبی به این معنی است که قضاوتی براساس نمونه صورت گرفته که با واقعیت فاصله زیادی دارد. البته واضح است که واقعیت را نمی‌دانیم ولی با توجه به توزیع آماری به نظر می‌رسد که قضاوت درستی صورت نگرفته.

چرا باید نمونه گیری کنیم؟

در صورتی که دسترسی به جامعه آماری، وجود داشته و محدودیتی از لحاظ هزینه‌های زمانی یا مالی نداشته باشیم، بهترین روش استفاده از جمعیت آماری و توصیف پدیده به کمک داده‌های جمع‌آوری شده از طریق سرشماری (Census) است. ولی اگر این شرایط وجود نداشته باشند، نمونه‌گیری بهترین راه حل خواهد بود. شاید علت نمونه‌گیری را بتوان یکی یا بعضی از شرایط زیر در نظر گرفت.

• کمبود زمان برای بررسی همه جامعه آماری
• افزایش بار مالی برای بررسی همه جمعیت آماری
• عدم دسترسی به همه جامعه آماری

بحث مربوط به زمان و هزینه‌های جمع‌آوری داده از جامعه کاملا واضح است. به هر حال ممکن است محدودیت‌هایی که در زمان انجام تحقیق یا بودجه‌ وجود دارد، ما را به اجبار به نمونه‌گیری وا دارد. ولی علت دیگری که باعث استفاده از نمونه‌گیری می‌شود، مخرب بودن ثبت اطلاعات از افراد جامعه است. برای مثال فرض کنید قرار است میانگین طول عمر لاستیک‌های یک کارخانه را مشخص کنیم. در صورتی که از جامعه آماری استفاده کنیم، کلیه لاستیک‌های تولید کارخانه باید فرسوده شده و طول عمرشان اندازه‌گیری شود. به این ترتیب هیچ محصولی به بازار عرضه نخواهد شد. به این منظور بهترین روش برای ثبت اطلاعات مربوط به عمر لاستیک‌ها، نمونه‌گیری خواهد بود.

نکته: در اغلب مباحث آماری، زمانی که ویژگی جامعه مورد بحث قرار گرفته باشد، شاخص‌های حاصل مانند معیارها مرکزی یا پراکندگی را «پارامتر جامعه» (Population Parameter) می‌شناسند. این پارامترها از خصوصیات اصلی جمعیت آماری بوده و به کمک آن‌ها درک بهتری از رفتار جامعه و پدیده تصادفی خواهیم داشت. در مقابل زمانی که همین شاخص‌ها از روی نمونه محاسبه شده و بدست آیند، آن‌ها را «آماره» (Statistics) یا برآورد می‌گویند. متوسط یا معدل اختلاف بین مقدار واقعی پارامتر و آماره یا برآورد آن توسط نمونه، همان اریبی خوانده می‌شود.

در فیلم آموزش آمار و احتمال مهندسی (حل تمرین و تست کنکور ارشد) به مفاهیم اولیه آمار بخصوص نمونه و جامعه، پرداخته شده که برای درک بهتر بخش‌های بعدی و پیشرفته آمار ضروری است. برای مشاهده این فیلم، به لینکی که در ادامه آورده شده، مراجعه کنید.

• برای مشاهده فیلم آموزش آمار و احتمال مهندسی (حل تمرین و تست کنکور ارشد) + اینجا کلیک کنید.

حجم نمونه چقدر باشد؟

دوباره به ضرب المثل «مشت نمونه خروار است» توجه می‌کنیم. به نظر شما اندازه این مشت که نماینده خروار خواهد بود، چقدر باید در نظر گرفته شود. از طرفی مقایسه مشت و خروار نشان می‌دهد که نسبت اندازه نمونه به اندازه جامعه باید بسیار کوچک باشد. از طرفی کوچک بودن نمونه ممکن است محقق را از درک ویژگی‌ها اصلی جامعه باز دارد. بنابراین باید حجم نمونه را به شکلی انتخاب کنیم که در نتایج حاصل، به یک خطای قابل قبول برسیم. حال فرض کنید که فاصله پارامتر از آماره را $$d$$و احتمال رخداد این خطا را با توجه به توزیع آماره حداکثر $$\alpha$$ در نظر بگیریم.

فیلم آموزش آمار و احتمال مهندسی – حل تمرین و تست کنکور ارشد در فرادرس

کلیک کنید

همچنین اریبی یا دقت برآورد نیز یکی دیگر از جنبه‌های اصلی برای تعیین حجم نمونه است. هر چه اریبی را کمتر در نظر بگیریم، حجم نمونه افزایش یافته و با افزایش اریبی، این میزان کاهش می‌یابد. برای میزان اریبی نیز بهتر است یک مقدار قابل تحمل در نظر بگیریم تا حجم نمونه قابل محاسبه شود.

فرض کنید که اندازه نمونه را $$n$$ در نظر گرفته‌ایم. مشخص است که بزرگ بودن اندازه جامعه، منجر به بزرگ بودن حجم نمونه هم خواهد شد. پس اگر $$N$$ را اندازه جامعه در نظر بگیریم، این مشخصه هم باید در تعیین اندازه نمونه دخیل باشد. بنابراین $$\frac{n}{N}$$ نیز یکی از پارامترهای مهم در تعیین اندازه نمونه خواهد بود.

همچنین توزیع یا پراکندگی ویژگی اندازه‌گیری شده از جامعه نیز در انتخاب حجم نمونه مناسب دخیل است. با توجه به شکل «توزیع» (Distribution) می‌دانیم که چه نقاطی یا مقادیر شانس رخداد بیشتری داشته و کدام مقادیر شانس کمتری برای دیده شدن دارند. واضح است که بهتر است از مشاهداتی که بیشتر محتمل هستند، نمونه بیشتری گرفته و از نقاطی که به ندرت دیده می‌شوند، تعداد کمتری را انتخاب کنیم. در نتیجه توزیع آماری جامعه نیز برای تعیین حجم نمونه مورد نیاز است.

یکی از پارامترهایی که شکل توزیع را دچار تغییر می‌کند، پراکندگی یا به اصطلاح واریانس است که نشان‌دهنده متوسط فاصله هر مشاهده از میانگین یا نقطه تمرکز آن‌ها است. هر چه واریانس یا پراکندگی بیشتر باشد باید نمونه‌های بیشتری جمع‌آوری شود تا نمونه (مشت) برآورد بهتری از جامعه (خروار) ارائه دهد.

به این ترتیب چهار عامل مختلف برای تعیین حجم نمونه مورد نظر خواهد بود که در ادامه فهرست شده‌اند.

• احتمال مبتنی بر خطای نمونه‌گیری
• میزان اریبی یا فاصله برآورد از مقدار پارامتر
• حجم جامعه
• توزیع جامعه آماری
• واریانس یا پراکندگی

این مشخصه‌ها را در یک فرمول جمع کرده و اگر توزیع را نرمال و فاصله برآورد با پارامتر را $$d$$ بنامیم، فرمول قابل ارائه برای استنباط پارامتر میانگین، به صورت زیر خواهد بود.

$$\large n  \geq \dfrac{z_{(1-\alpha/2)}^2 \times \sigma^2 }{ d^2}$$

برای مثال اگر منظور از یک تحقیق آماری و نمونه‌گیری، آزمون برای بررسی میانگین میزان فشار خون باشد و بخواهیم بک آزمون با خطای $$0.05$$ با اریبی یا فاصله پارامتر از برآورد برابر با ۶ واحد ایجاد کنیم، با فرض اینکه فشار خون دارای انحراف استاندارد ۱۵ واحد و توزیع نرمال است، احتیاج به یک نمونه حداقل ۱۰۰ تایی داریم، زیرا:

• $$\alpha = 0.05$$ و $$z_{1-\alpha/2} \approx 2$$
• $$d= 6$$
• $$\sigma^2 = (15)^2$$

پس نتیجه محاسبه فرمول بالا برای تعیین اندازه نمونه آماری به صورت زیر درخواهد آمد.

$$n = \dfrac{16( 15^2 )}{ 6^2 }= 100$$

نکته: از آنجا که توزیع را نرمال در نظر گرفته‌ایم، حجم جامعه آماری را تقریبا بی‌نهایت فرض کرده‌ایم، در نتیجه اثری از $$N$$ در فرمول مربوط به تعیین حجم نمونه آماری دیده نمی‌شود.

خلاصه و جمع‌بندی

در این متن به یک موضوع مهم آماری یعنی نمونه آماری و ویژگی‌های آن پرداختیم تا بتوانیم به کمک جمع آوری نمونه، در مورد جامعه به بهترین قضاوت برسیم. نمونه‌گیری نامناسب باعث ایجاد اریبی در استنباط آماری شده و نتایج حاصل قابل اعتماد نیستند. به این معنی که با تغییر کوچکی در بعضی مشاهدات، نتایج به شکل عمیقی تغییر خواهند یافت. این موضوع حساسیت زیاد به نمونه را نشان داده که از لحاظ آماری، امری ناسزا و نکوهیده است. بنابراین نمونه آماری و روش نمونه‌گیری، تعیین حجم نمونه و تکنیک آماری مناسب، تضمینی برای خلاصی از اریبی و ایجاد برآوردهای نااریب هستند که بخصوص خطای نمونه‌گیری را کاهش می‌دهند.