نمودار مکان زمان – توضیح به زبان ساده + حل مثال

جابجایی جسم، برابر تغییر مکان جسم و کمیتی برداری و دارای جهت و اندازه است. جابجایی را می‌توان به صورت $$\triangle x = x_f - x_ i$$ نوشت. نمودار مکان زمان یا جابجایی زمان جسمی متحرک، مکان یا جابجایی آن را برحسب زمان به ما نشان می‌دهد. اگر نمودار مکان برحسب زمان جسمی را داشته باشیم، اطلاعات مهمی مانند سرعت و شتاب حرکت را می‌توانیم به راحتی به‌دست آوریم. در این مطلب، ابتدا نمودار مکان زمان را به زبان ساده توضیح می‌دهیم، سپس در مورد اطلاعاتی که این نمودار به ما می‌دهد با حل مثال‌های مختلف، صحبت می‌کنیم.

نمودار مکان زمان چیست ؟

به کمک نمودار مکان زمان، اطلاعات بسیار مهمی را در مورد حرکت اجسام مختلف به‌دست می‌آوریم. محور عمودی در نمودار مکان زمان، مکان جسم را نسبت به مبدأ و محور افقی، زمان را نشان می‌دهد.

به عنوان مثال، مکان جسمی را در زمانی مشخص با استفاده از نمودار زیر می‌خوانید. عدد خوانده شده، مکان جسم برحسب متر را به ما نشان می‌دهد. نقطه سبزرنگ در نمودار زیر ابتدا در مبدأ مختصات قرار دارد. اگر آن را روی محور افقی (زمان) به سمت راست حرکت دهیم، مکان جسم تغییر خواهد کرد. به عنوان مثال، اگر نقطه سبز را روی عدد ۳ قرار دهیم، مکان ذره برابر ۴+ متر خواهد بود.

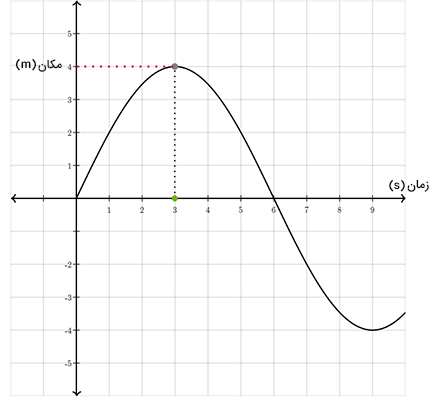
پرسش ۱:‌ با توجه به نمودار مکان زمان نشان داده شده در بالا، جسم در زمان ۵ ثانیه در چه مکانی قرار دارد؟

پاسخ: مکان جسم در زمان ۵ ثانیه برابر ۲ متر خواهد بود.

پرسش ۲: مکان جسم در چه زمانی برابر صفر است؟

پاسخ: مکان جسم در زمان‌های صفر و ۶ ثانیه برابر صفر است. یعنی جسم، شش ثانیه پس از شروع حرکت بار دیگر به مبدأ مختصات بازمی‌گردد.

چه اطلاعاتی را می توان از نمودار مکان زمان به دست آورد ؟

نمودار مکان زمان اطلاعاتی در مورد مسافت، جابجایی، سرعت، تندی و شتاب جسم به ما می‌دهد. در ادامه، در مورد هر یک از کمیت‌های گفته شده با جزییات بیشتری صحبت خواهیم کرد.

شیب نمودار مکان زمان چه چیزی را نشان می دهد ؟

شیب خط مماس بر نمودار مکان زمان، بیان‌گر سرعت حرکت جسم است. بنابراین، مقدار شیب خط مماس بر نمودار مکان زمان در هر لحظه از زمان، سرعت جسم را در آن لحظه به می‌دهد. سوالی که ممکن است مطرح شود آن است که چرا شیب خط مماس بر نمودار مکان زمان، سرعت جسم را نشان می‌دهد. برای پاسخ به این پرسش، نمودار خطی مکان زمان نشان داده شده در تصویر زیر را در نظر بگیرید.

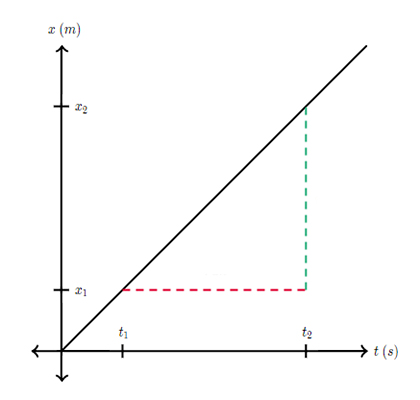
در تصویر بالا نمودار مکان زمان به صورت خط مستقیمی رسم شده است. شیب این خط برابر است با:

$$m = \frac{x _ 2 - x_ 1}{t _2 - t_ 1}$$

رابطه به‌دست آمده برای شیب خط در نمودار مکان زمان، مشابه تعریف سرعت حرکت جسم است:

$$v = \frac {\triangle x } { \triangle t } = \frac{x _ 2 - x_ 1}{t _2 - t_ 1}$$

توجه به این نکته مهم است که چه شیب نمودار مکان زمان ثابت باشد چه متغیر، مقدار آن برابر سرعت جسم خواهد بود. به عنوان مثال، خط قرمز مماس بر نمودار مکان زمان در تصویر زیر، شیب را در زمانی مشخص (مبدأ) نشان می‌دهد. با حرکت نقطه سبز روی نمودار، شیب خط قرمز تغییر خواهد کرد. شیب خط در ثانیه‌های سوم و نهم حرکت، برابر صفر است.

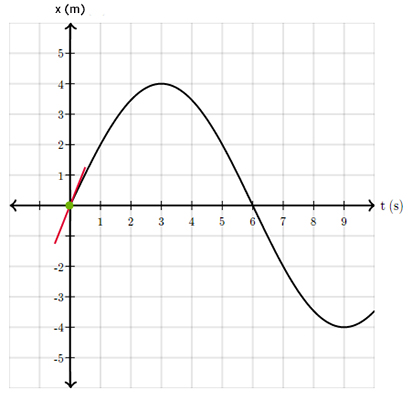
پرسش ۳: چرا محور عمودی در نمودار مکان زمان، $$x$$ نامیده می‌شود؟

پاسخ: در ریاضیات، محور عمودی در دستگاه مختصات دوبعدی، $$y$$ و محور افقی $$x$$ نامیده می‌شوند. اما در فیزیک، محور افقی را به صورت قراردادی زمان و محور عمودی را با توجه به نوع نمودار، مکان ($$x$$)، سرعت ($$v$$) یا شتاب ($$a$$) قرار می‌دهیم.

نکته ۱: اگر زاویه خط مماس بر نمودار مکان زمان با محور افقی، کوچک‌تر از ۹۰ درجه باشد، شیب خط مثبت خواهد بود. در مقابل، اگر زاویه خط مماس بر نمودار مکان زمان با محور افقی، بزرگ‌تر از ۹۰ درجه باشد، شیب خط منفی است. همچنین، اگر زاویه خط با محور زمان برابر صفر یا ۹۰ درجه باشد، شیب آن به ترتیب برابر صفر و بی‌نهایت خواهد بود.

پرسش ۴: شیب خط مماس بر نمودار مکان زمان نشان داده شده در تصویر بالا در چه زمان‌هایی مثبت، منفی و صفر است؟

پاسخ: با توجه به زاویه خط مماس بر نمودار مکان زمان نسبت به محور افقی، شیب، بین زمان‌‌های صفر تا ۳ ثانیه مثبت و در بازه زمانی بین ۳ تا ۹ ثانیه، منفی خواهد بود. همچنین، خط مماس بر نمودار در زمان‌های ۳ و ۹ ثانیه، موازی محور افقی است، بنابراین شیب در این زمان‌ها برابر صفر است.

اگر شیب نمودار مکان زمان مثبت باشد، سرعت حرکت جسم مثبت است و اگر شیب نمودار منفی باشد، سرعت حرکت جسم منفی خواهد بود. سرعت منفی به چه معنا است؟ در مسئله‌های حرکت بر خط راست در فیزیک، جهتی را به عنوان جهت مثبت انتخاب می‌کنند. اگر جسم در راستای جهت مثبت حرکت کند، سرعت آن مثبت و اگر در خلاف جهت آن حرکت کند، سرعت آن منفی خواهد بود.

نکته ۲: شیب خط مماس بر نمودار مکان زمان، سرعت لحظه‌ای جسم را در آن زمان به ما می‌دهد. همچنین، شیب خط متصل‌کننده دو نقطه در دو زمان مختلف روی نمودار، سرعت متوسط بین آن دو زمان را به ما نشان می‌دهد.

انحنای نمودار مکان زمان

نمودار مکان زمان ممکن است خط یا منحنی باشد. اگر نمودار منحنی باشد، انحنای آن نقش مهمی در توصیف حرکت جسم ایفا می‌کند. همچنین، شیب خط مماس بر منحنی، ثابت نیست و از نقطه‌ای به نقطه دیگر، تغییر خواهد کرد. تغییرات شیب، به معنای تغییرات سرعت حرکت جسم است. همچنین، تغییرات سرعت سبب ایجاد حرکت شتاب‌دار می‌شود. در نتیجه، انحنا در نمودار مکان زمان، حرکت شتاب‌دار را نشان می‌دهد. نمودار مکان زمان نشان داده شده در تصویر زیر را در نظر بگیرید. با حرکت نقطه سبزرنگ به سمت راست، شیب خط مماس قرمزرنگ تغییر خواهد کرد. به عنوان مثال، با حرکت نقطه سبز از زمان صفر به زمان ۳ ثانیه، شیب خط قرمز کاهش می‌یابد و به صفر می‌رسد.

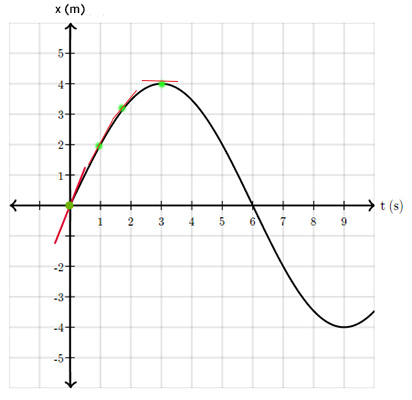
شیب خط مماس بر نمودار، پس از زمان سه ثانیه، منفی و در بازه زمانی صفر تا ۶ ثانیه، شیب خط مماس از مثبت به منفی تغییر کرده و تقعر نمودار، به سمت پایین است. در این حالت، شتاب حرکت جسم منفی خواهد بود. در مقابل، شیب خط مماس بر نمودار در بازه زمانی ۶ تا ۹ ثانیه، از منفی به مثبت تغییر کرده و تقعر نمودار، به سمت بالا است. در این حالت، جسم با شتاب مثبت، حرکت می‌کند.

پرسش ۵: با توجه به نمودار مکان زمان نشان داده شده در تصویر بالا، شتاب حرکت جسم در زمان ۶ ثانیه چقدر است؟

پاسخ: از آنجا که شیب نمودار در اطراف زمان ۶ ثانیه، تقریبا ثابت است و تغییرات زیادی ندارد، شتاب در این زمان برابر صفر است.

در مطالب بالا گفتیم که شیب نمودار مکان زمان در هر لحظه، سرعت جسم را در آن لحظه به ما می‌دهد. در ادامه، در مورد چگونگی به‌دست آوردن سرعت و تندی با استفاده از نمودار مکان زمان صحبت می‌کنیم.

جابجایی و مسافت در نمودار مکان زمان

مسافت کمیتی نرده‌ای و جابجایی کمیتی برداری است. مسافت، به صورت طول مسیر طی شده توسط جسم، تعریف می‌شود. بنابراین، به شکل مسیر طی شده وابسته است. در مقابل، جابجایی را به صورت کوتاه‌ترین مسیر بین دو نقطه (نقطه آغاز و پایان)، تعریف می‌کنیم. در نتیجه، جابجایی، برخلاف مسافت، تنها به نقاط ابتدا و انتهای مسیر بستگی دارد. تفاوت مهم دیگر بین مسافت و جابجایی آن است که مسافت طی شده توسط جسم همواره مثبت است. در حالی‌که، جابجایی ممکن است مثبت یا منفی باشد. برای به‌دست آوردن جابجایی در بازه زمانی مشخص از روی نمودار مکان زمان، به مکان جسم در نقطه ابتدا و انتهای بازه زمانی توجه می‌کنیم. نمودار مکان زمان داده شده در تصویر زیر را در نظر بگیرید.

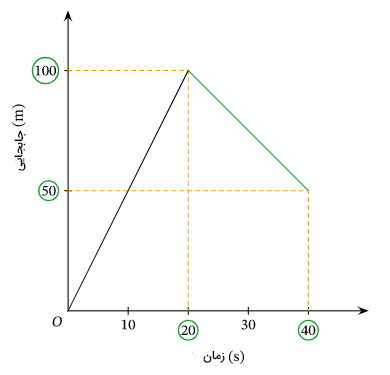
جابجایی جسم در بازه زمانی ۲۰ تا ۴۰ ثانیه چه مقدار است؟ برای به‌دست آوردن جابجایی در این بازه زمانی، ابتدا مکان‌های جسم در ابتدای بازه، زمان ۲۰ ثانیه، و انتهای بازه، زمان ۴۰ ثانیه، را به‌دست می‌آوریم. مکان جسم در زمان ۲۰ ثانیه برابر ۵۰ متر و در زمان ۴۰ ثانیه برابر ۱۰۰ متر است. بنابراین جابجایی برابر است:

متر 50 = ۱۰۰ متر - ۵۰ متر = جابجایی جسم در ۲۰ ثانیه

پرسش ۶: جابجایی جسم در مدت زمان ۴۰ ثانیه چه مقدار است؟

پاسخ: ابتدا مکان جسم را در زمان‌های صفر و ۴۰ ثانیه به‌دست می‌آوریم. جسم در زمان صفر در مکان صفر و در زمان ۴۰ ثانیه در مکان ۵۰ متر قرار دارد. بنابراین، جابجایی آن برابر ۵۰ متر است.

برای به‌دست آوردن مسافت جسم از روی نمودار مکان زمان به نقطه‌های ابتدا و انتهای مسیر کاری نداریم، بلکه به مسیر طی شده توسط جسم توجه می‌کنیم. به عنوان مثال، برای به‌دست آوردن مسافت طی شده توسط جسم در ۴۰ ثانی اول حرکت به بخش‌های مختلف نمودار توجه می‌کنیم. نمودار مکان زمان جسم در تصویر بالا به دو بخش تقسیم می‌شود:

1. در بخش اول، ۲۰ ثانیه با سرعت ثابت و مثبت حرکت می‌کند و به ۱۰۰ متری مبدأ حرکت می‌رسد.
2. در بخش دوم حرکت، سرعت جسم ثابت و منفی است. بنابراین، جسم پس از رسیدن به مکان ۱۰۰ متری، در خلاف جهت مثبت و به سمت مبدأ شروع به حرکت می‌کند و پس از ۲۰ ثانیه به ۵۰ متری مبدأ می‌رسد.
3. مسافت طی شده توسط جسم در بخش اول حرکت، برابر ۱۰۰ متر و در بخش دوم، برابر ۵۰ متر است. در نتیجه، مسافت کل در ۴۰ ثانیه برابر ۱۵۰ متر خواهد بود.

با به‌دست آوردن مسافت و جابجایی کل، به راحتی می‌توان سرعت و تندی متوسط را محاسبه کرد.

انواع نمودارهای مکان زمان

حرکت جسم در فیزیک به چهار دسته کلی زیر تقسیم می‌شود:

• حالت سکون: در این حالت جسم ساکن است و مکان آن نسبت به زمان تغییر نمی‌کند. بنابراین، شتاب و حرکت آن نیز برابر صفر هستند.
• حرکت با سرعت یکنواخت: در این حالت، مکان جسم نسبت به زمان با آهنگ ثابتی تغییر می‌کند. به بیان دیگر، جابجایی جسم در بازه‌های زمانی یکسان، برابر است.
• حرکت با شتاب ثابت: در این حرکت، شتاب جسم به طور یکنواخت تغییر می‌کند. به بیان‌ دیگر، شتاب حرکت جسم یا تغییرات سرعت نسبت به زمان، ثابت است.
• حرکت با شتاب متغیر: در این حرکت، شتاب جسم نسبت به زمان، به طور پیوسته تغییر می‌کند.

نمودار مکان زمان برای جسم ساکن

هنگامی که جسم ساکن باشد، سرعت آن برابر صفر خواهد بود. صفر بودن سرعت به معنای ثابت بودن مکان نسبت به زمان است. بنابراین، نمودار مکان زمانِ جسم ساکن به شکل خطی مستقیم و افقی رسم می‌شود. همان‌طور که در تصویر زیر مشاهده می‌شود، شیب نمودار مکان زمان برای جسم ساکن برابر صفر است.

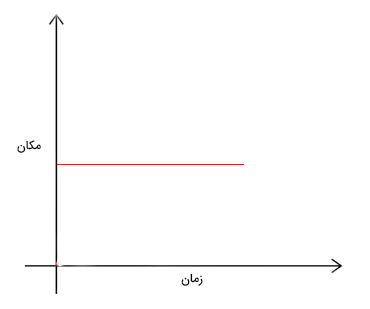
نمودار مکان زمان برای حرکت یکنواخت

حرکت یکنواخت هنگامی رخ می‌دهد که جسمی روی خط مستقیم با سرعت ثابت، حرکت می‌کند. نمودار مکان زمانِ حرکت یکنواخت چگونه است؟ در مطالب بالا گفتیم، شیب نمودار مکان زمان، سرعت حرکت را نشان می‌دهد. از آنجا که سرعت حرکت جسم در حرکت یکنواخت ثابت است، شیب نمودار مکان زمان نیز باید ثابت باشد. در نتیجه، نمودار، خطی مستقیم با شیب ثابت و غیرصفر خواهد بود.

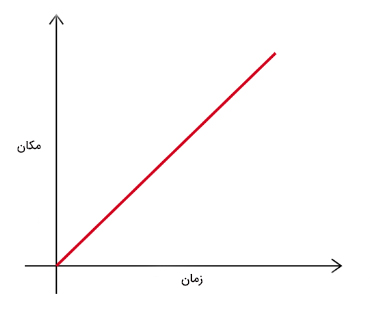
مثال اول برای حرکت یکنواخت

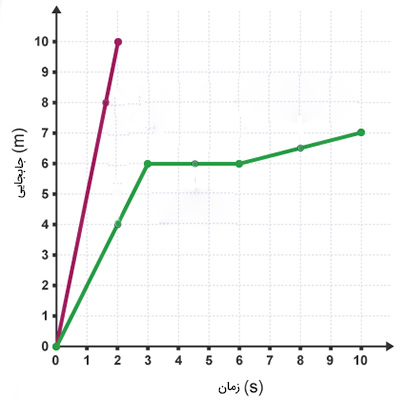
نمودار مکان زمان دو جسم در نمودار زیر با رنگ‌های سبز و قرمز نشان داده شده است. مطلوب است:

• تندی متوسط جسم سبز در بازه زمانی صفر تا ۱۰ ثانیه.
• تندی متوسط جسم قرمز در بازه زمانی صفر تا دو ثانیه.

پاسخ

ابتدا تندی متوسط جسم سبزرنگ را به‌دست می‌آوریم. برای به‌دست آوردن تندی متوسط باید ابتدا مسافت کل جسم را محاسبه کنیم. نمودار مکان زمان جسم سبز از سه قسمت تشکیل شده است:

1. سه ثانیه اول حرکت: جسم از مبدأ شروع به حرکت می‌کند و در زمان سه ثانیه به شش متری آن می‌رسد. نمودار مکان زمان در این قسمت، خطی با شیب مثبت و ثابت است. بنابراین، جسم در سه ثانیه اول حرکت با سرعت ثابت حرکت می‌کند.
2. حرکت بین زمان‌های ۳ تا ۶ ثانیه: نمودار مکان زمان در این قسمت، خطی افقی با شیب صفر است. بنابراین، جسم پس از ۶ متر جابجایی، به مدت ۳ ثانیه متوقف می‌شود.
3. حرکت بین زمان‌های ۶ تا ۱۰ ثانیه: جسم پس از توقف ۳ ثانیه‌ای با سرعت ثابت شروع به حرکت می‌کند. نمودار مکان زمان در این قسمت نیز، همانند قسمت اول، خطی با شیب ثابت و مثبت است.

مسافت کل طی شده توسط جسم سبز برابر ۶ متر در قسمت اول حرکت و یک متر در قسمت آخر حرکت است. از آنجا که جسم سبز این مسافت را در مدت زمان ۱۰ ثانیه طی کرده است، تندی متوسط آن برابر است با:

$$S_{avg} = \frac{7 m}{10 s} = 0.7 \frac {m} { s }$$

نمودار مکان زمان جسم قرمز از یک قسمت تشکیل شده است. جسم از مبدأ شروع به حرکت می‌کند و پس از ۲ ثانیه، ده متر جابجا می‌شود. بنابراین، تندی متوسط آن برابر است با:

$$S_{avg} = \frac{10 m}{2 s} = 5 \frac {m} { s }$$

مثال دوم حرکت یکنواخت

با توجه به نمودار مکان زمان نشان داده شده در ادامه، به پرسش‌های زیر پاسخ دهید.

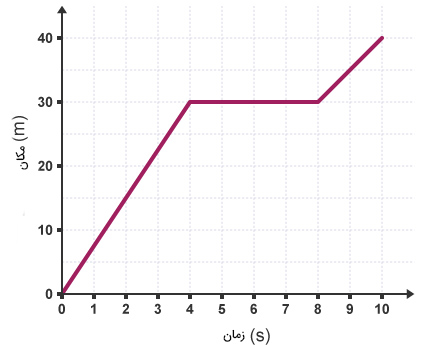
نمودار مکان زمان جسم از سه قسمت تشکیل شده است:

1. چهار ثانیه اول حرکت: جسم از مبدأ شروع به حرکت می‌کند و در زمان چهار ثانیه به ۳۰ متری آن می‌رسد. نمودار مکان زمان در این قسمت، خطی با شیب مثبت و ثابت است. بنابراین، جسم در چهار ثانیه اول حرکت با سرعت ثابت حرکت می‌کند.
2. حرکت بین زمان‌های ۴ تا ۸ ثانیه: نمودار مکان زمان در این قسمت، خطی افقی با شیب صفر است. بنابراین، جسم پس از ۳۰ متر جابجایی، به مدت ۴ ثانیه متوقف می‌شود.
3. حرکت بین زمان‌های ۸ تا ۱۰ ثانیه: جسم پس از توقف ۳ ثانیه‌ای با سرعت ثابت شروع به حرکت می‌کند. نمودار مکان زمان در این قسمت نیز، همانند قسمت اول، خطی با شیب ثابت و مثبت است.

پرسش: جسم در ۴ ثانیه اول حرکت، چه مسافتی شده است؟

پاسخ: ۳۰ متر.

پرسش: تندی جسم در ۴ ثانیه اول حرکت چه مقدار است؟

پاسخ: برای محاسبه تندی، ابتدا باید مسافت و زمان کل را داشته باشیم. مسافت طی شده توسط جیم در ۴ ثانیه اول حرکت برابر ۳۰ متر است، بنابراین تندی آن برابر است با:

$$S_{avg} = \frac{30 m}{4 s} = 7. 5 \frac {m} { s }$$

پرسش: جسم برای چه مدت زمانی، ساکن باقی می‌ماند؟

پاسخ: نمودار مکان زمان برای جسم ساکن، خطی مستقیم و افقی با شیب صفر است. بنابراین، جسم از زمان ۴ ثانیه تا زمان ۸ ثانیه، ساکن باقی می‌ماند.

پرسش: تندی متوسط جسم در تمام طول مسیر، چه مقدار است؟

پاسخ: مسافت طی شده توسط جسم در ۱۰ ثانیه برابر ۴۰ متر است. بنابراین، تندی متوسط در تمام مسیر برابر است با:

$$S_{avg} = \frac{40 m}{10 s} = 4 \frac {m} { s }$$

مثال سوم حرکت یکنواخت

با توجه به نمودار مکان زمان نشان داده شده در تصویر زیر، به پرسش‌های مطرح شده پاسخ دهید.

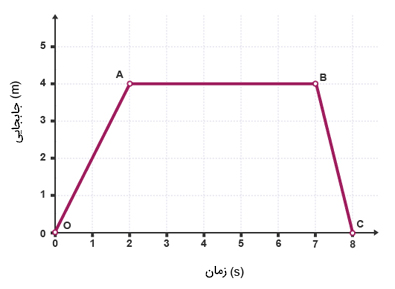
پرسش: حرکت در بخش OA را توصیف کنید.

پاسخ: برای توصیف حرکت جسم در این بخش، به اطلاعات زیر نیاز داریم:

• نوع نمودار مکان زمان
• شیب نمودار
• مثبت یا منفی بودن شیب

نمودار در قسمت OA، خطی با شیب ثابت و مثبت است. بنابراین، جسم در دو ثانیه اول حرکت با سرعت ثابت و مثبت شروع به حرکت می‌کند. برای به‌دست آوردن سرعت متوسط حرکت در این قسمت، جابجایی انجام شده را بر مدت زمان جابجایی تقسیم می‌کنیم.

$$v_{avg} = \frac{4 m}{2 s} = 2 \frac {m} { s }$$

پرسش: حرکت در بخش‌های AB و BC را توصیف کنید.

پاسخ: در قسمت AB، نمودار مکان زمان خطی افقی با شیب صفر است، بنابراین جسم پس از ۴ متر جابجایی به مدت ۵ ثانیه متوقف می‌شود. نمودار مکان زمان در قسمت BC، خطی با شیب ثابت و منفی است. از این‌رو، جسم در این قسمت با سرعت منفی شروع به حرکت می‌کند. سرعت منفی به معنای حرکت در خلاف جهت مثبت قراردادی است. به عنوان مثال، اگر حرکت به سمت راست را مثبت در نظر گرفته باشیم، جسم به سمت چپ حرکت می‌کند. جابجایی جسم در این قسمت برابر 4- متر و مدت زمان جابجایی برابر یک ثانیه است. در نتیجه، سرعت متوسط برابر است با:

$$v_{avg} = \frac{- 4 m}{1 s} = - 4 \frac {m} { s }$$

پرسش: سرعت و تندی متوسط در کل مسیر را به‌دست آورید.

پاسخ: برای به‌دست آوردن سرعت متوسط در کل مسیر، جابجایی کل جسم را به‌دست می‌آوریم. همان‌طور که در بالا گفته شد، جسم از مبدأ شروع به حرکت می‌کند و پس از ۴ متر جابجایی، به مدت ۵ ثانیه متوقف می‌شود. سپس، در خلاف جهت شروع به حرکت می‌کند و به مبدأ بازمی‌گردد. از این‌رو، جابجایی کل جسم در تمام مسیر حرکت، برابر صفر است. در نتیجه، سرعت متوسط نیز برابر صفر خواهد بود.

برای محاسبه تندی متوسط، مسافت کل طی شده توسط جسم را در طول حرکت به‌دست می‌آوریم. حرکت جسم به صورت شماتیک در تصویر زیر نشان داده شده است.

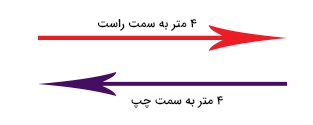
با توجه به تصویر نشان داده شده در بالا، مسافت کل طی شده توسط جسم برابر ۸ متر است. در نتیجه، تندی متوسط برابر است با:

$$S_{avg} = \frac{8 m}{8 s} = 1 \frac {m} { s }$$

مثال چهارم حرکت یکنواخت

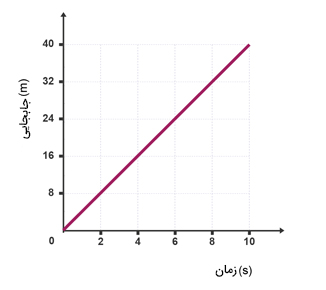
کودکی با سرعت ثابت می‌دود. نمودار مکان زمان او در ده ثانیه اول دویدن،‌ به صورت زیر است. مطلوب است:

1. جابجایی کودک پس از ۶ ثانیه چه مقدار است؟
2. سرعت دویدن کودک را به‌دست آورید.
3. اگر کودک با سرعت یکسانی به دویدن ادامه دهد، پس از ۲۲ ثانیه چه مسافتی را طی خواهد کرد؟

پاسخ

نمودار مکان زمان کودک به هنگام دویدن خط مستقیمی با شیب ثابت و مثبت است. برای به‌دست آوردن جابجایی کودک پس از ۶ ثانیه از شروع حرکت، به این نمودار مراجعه می‌کنیم. ابتدا خطی موازی محور مکان که از زمان ۶ ثانیه می‌گذرد، به صورت زیر رسم می‌‌کنیم.

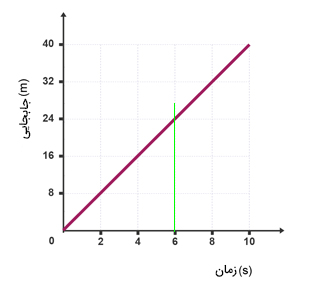
از محل تقاطع نمودار مکان زمان و خط سبز، خطی موازی محور زمان، رسم می‌کنیم. محل تقاطع این خط با محور مکان، جابجایی کودک در ۶ ثانیه اول حرکت را نشان می‌دهد. بنابراین، کودک ۶ ثانیه پس از شروع حرکت، ۲۴ متر جابجا شده است.

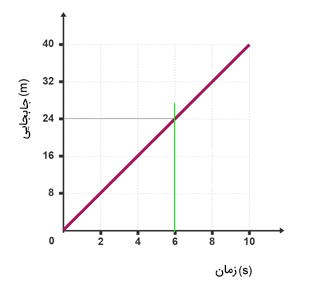
برای به‌دست آوردن سرعت کودک دو راه داریم:

1. انتخاب دو نقطه دلخواه روی نمودار مکان زمان و به‌دست آوردن شیب خط
2. تقسیم جابجایی در کل مسیر بر زمان جابجایی

ابتدا، دو نقطه $$( 0 \, 0 )$$ و $$(6 \, 24 )$$ را روی نمودار انتخاب می‌کنیم و شیب خط گذرنده از آن‌ها را به‌دست می‌آوریم:

$$v = m = \frac{x_ 2 - x_ 1}{t _2 - t _ 1} = \frac{24 m - 0 m }{6 s - 0 s} = \frac{24 m}{6 s} = 4 \frac {m} { s }$$

شیب خط و در نتیجه، سرعت متوسط کودک برابر ۶ متر بر ثانیه است. در ادامه، سرعت را از تقسیم جابجایی بر زمان به‌دست می‌آوریم. کودک در مدت زمان ده ثانیه به اندازه ۴۰ متر جابجا شده است. بنابراین، سرعت متوسط آن برابر است با:

$$v_{avg} = \frac{40 m}{10 s} = 4 \frac {m} { s }$$

مثال پنجم حرکت یکنواخت

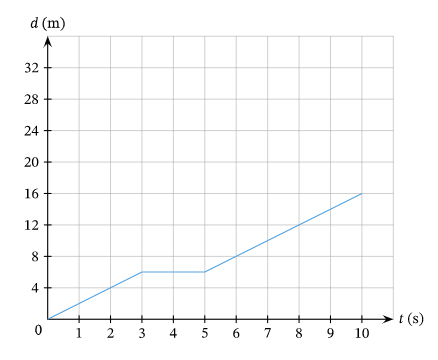
نمودار مکان زمان ذره‌ای به هنگام حرکت روی خط راست، به صورت زیر نشان داده شده است. سرعت متوسط در کل مسیر حرکت را به‌دست آورید.

پاسخ

سرعت متوسط برابر جابجایی کل تقسیم بر زمان کل است. قبل از حل این مثال به این نکته توجه داشته باشید که اگر نمودار مکان زمان جسمی، خط‌هایی با شیب‌های ثابت و مثبت باشند، جسم در یک راستا حرکت می‌کند. بنابراین، جابجایی و مسافت با یکدیگر برابر هستند. اما اگر در بخش‌هایی از نمودار، شیب خطی منفی باشد، جسم در راستای مخالف حرکت کرده است. بنابراین، جابجایی و مسافت با یکدیگر برابر نخواهند بود. با توجه به نمودار مکان زمان نشان داده شده در بالا، حرکت جسم به سه مرحله تقسیم می‌شود:

1. مرحله اول بین زمان‌های صفر تا ۳ ثانیه رخ می‌دهد. نمودار مکان زمان در این بازه زمانی، خطی با شیب ثابت و مثبت است. بنابراین، جسم در بازه زمانی صفر تا ۳ ثانیه، با سرعت ثابت و مثبت از مبدأ دور می‌شود. جابجایی در این مرحله، برابر ۶ متر است.
2. مرحله دوم در بازه زمانی ۳ تا ۵ ثانیه اتفاق می‌افند. نمودار مکان زمان در این مدت خطی افقی با شیب صفر است. در نتیجه، جسم ۳ ثانیه پس از شروع حرکت، به مدت ۲ ثانیه متوقف می‌شود. جابجای این مرحله برابر صفر است.
3. مرحله سوم بین زمان‌های ۵ تا 10 ثانیه رخ می‌دهد. نمودار مکان زمان در این بازه زمانی، خطی با شیب ثابت و مثبت است. بنابراین، جسم در بازه زمانی ۵ تا ۱۰ ثانیه، با سرعت ثابت و مثبت و بدون تغییر جهت،‌ به حرکت خود ادامه می‌دهد و از مکان ۶ متر به ۱۶ متر می‌رسد. جابجایی در این مرحله، برابر ۱۰ متر است.

بنابراین، جابجایی کل جسم در مدت زمان ۱۰ ثانیه برابر $$6 m + 0 + 10 m = 16 m$$ است. با داشتن جابجایی و زمان، سرعت متوسط را به‌دست می‌آوریم:

$$v_{avg} = \frac{16 m}{10 s} = 1. 6 \frac {m} { s }$$

مثال ششم حرکت یکنواخت

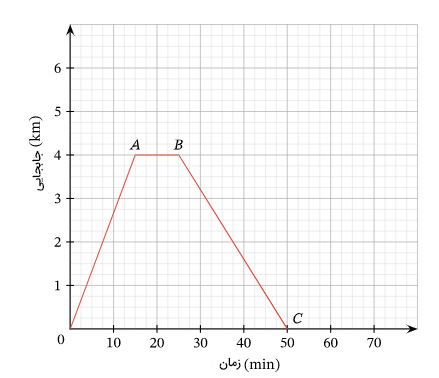
نمودار مکان زمان دوچرخه‌سواری در حرکت بر روی خط راست به صورت زیر نشان داده شده است. سرعت متوسط دوچرخه‌سوار را در هر قسمت حرکت برحسب کیلومتر بر ساعت به‌دست آورید.

پاسخ

در این مثال، از ما خواسته شده که سرعت متوسط را در هر مرحله از حرکت دوچرخه‌سوار به‌دست آوریم. در مطالب بالا گفتیم که شیب نمودار مکان زمان، سرعت حرکت را به ما می‌دهد. بنابراین، حرکت دوچرخه‌سوار به سه مرحله تقسیم می‌شود:

• مرحله OA: در این مرحله ۱۵ دقیقه‌ای، شیب خطِ نمودار مکان زمان، ثابت و مثبت است. بنابراین دوچرخه‌سوار از مبدأ با سرعت ثابت و مثبت شروع به حرکت می‌کند و پس از ۱۵ دقیقه، به ۴ کیلومتری مبدأ حرکت می‌رسد. بنابراین، جابجایی دوچرخه‌سوار در مدت ۱۵ دقیقه برابر ۴ کیلومتر است. از این‌رو، سرعت متوسط برابر است با:

$$v_{avg} = \frac{4 m}{0.25 h} = 1 6 \frac {km} { h }$$

توجه به این نکته مهم است که سرعت متوسط برحسب کیلومتر بر ساعت خواسته شده است. بنابراین، ۱۵ دقیقه را به ساعت تبدیل کردیم.

• مرحله AB: این مرحله ۱۰ دقیقه‌ای، خط ثابتی با شیب صفر است. بنابراین، دوچرخه‌سوار پس از ۱۵ دقیقه رکاب زدن تصمیم می‌گیرد به مدت ده دقیقه استراحت کند. از آنجا که جابجایی در این مرحله برابر صفر است، سرعت متوسط نیز برابر صفر خواهد بود.
• مرحله BC: در این مرحله ۲۵ دقیقه‌ای، شیب خط نمودار مکان زمان، ثابت و منفی است. بنابراین دوچرخه‌سوار پس از استراحت با سرعت ثابت و منفی، در خلاف جهت و به سمت مبدأ حرکت می‌کند و پس از ۲۵ دقیقه، به نقطه ابتدایی حرکت می‌رسد. بنابراین، جابجایی دوچرخه‌سوار در مدت ۲۵ دقیقه برابر ۴- کیلومتر است. از این‌رو، سرعت متوسط برابر است با:

$$v_{avg} = \frac{- 4 m}{0.42 h} = - 9.5 \frac {km} { h }$$

مثال هفتم حرکت یکنواخت

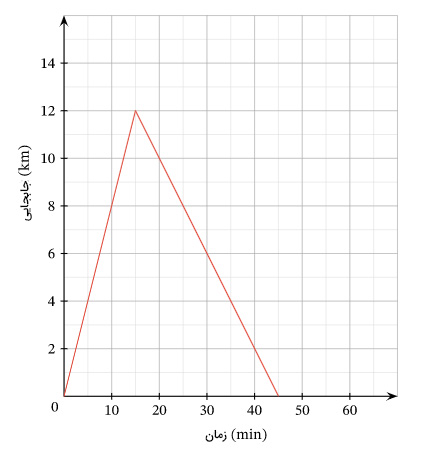
نمودار مکان زمان ذره‌ای به هنگام حرکت بر روی خط راست به صورت زیر نشان داده شده است. این ذره پس از شروع حرکت از مبدأ، به مدت ۱۵ دقیقه از آن دور می‌شود و سپس با تغییر جهت حرکت به مبدأ بازمی‌گردد. مطلوب است:

1. تندی متوسط را در کل مسیر برحسب کیلومتر بر ساعت به‌دست آورید.
2. سرعت متوسط را در کل مسیر برحسب کیلومتر بر ساعت به‌دست آورید.

پاسخ

با توجه به آن‌که نمودار مکان زمان از دو خط با شیب‌های متفاوت تشکیل شده است، حرکت ذره به دو مرحله تقسیم می‌شود:

• زمان صفر تا ۱۵ ثانیه: در این مرحله، نمودار مکان زمان، خطی با شیب مثبت و ثابت است. بنابراین، ذره از مبدأ با سرعت ثابت و مثبت شروع به حرکت می‌کند و پس از ۱۵ ثانیه به ۱۲ کیلومتری مبدأ می‌رسد. جابجایی و مسافت طی شده توسط ذره در این مرحله به ترتیب برابر ۱۲+ و ۱۲ کیلومتر است.
• زمان ۱۵ تا ۴۵ ثانیه: در این مرحله، نمودار مکان زمان، خطی با شیب منفی و ثابت است. بنابراین، ذره با سرعت ثابت و منفی به حرکت خود ادامه می‌دهد و پس از ۴۵ ثانیه به مبدأ حرکت بازمی‌گردد. جابجایی و مسافت طی شده توسط ذره در این مرحله به ترتیب برابر ۱۲- و ۱۲ کیلومتر است.

در ابتدا، تندی متوسط در کل مسیر را به‌دست می‌آوریم. برای به‌دست آوردن تندی متوسط در تمام مسیر باید مسافت کل طی شده توسط ذره را محاسبه کنیم. مسافت ذره در مرحله اول حرکت برابر ۱۲ کیلومتر و در مرحله دوم نیز برابر ۱۲ کیلومتر است. بنابراین مسافت کل برابر ۲۴ کیلومتر خواهد بود:

$$S_{avg} = \frac{24 km}{0.75 h} = 32 \frac {km} { h }$$

برای به‌دست اوردن سرعت متوسط در کل مسیر، جابجایی کل را به‌دست می‌آوریم. از آنجا که جابجایی ذره در مرحله اول حرکت برابر ۱۲ کیلومتر و در مرحله دوم حرکت برابر ۱۲- کیلومتر است، جابجایی کل برابر صفر خواهد بود. در نتیجه، سرعت متوسط در کل مسیر، صفر می‌شود.

مثال هشتم حرکت یکنواخت

حیوانی به جرم ۳/۲ کیلوگرم، روی زمین به سمت جلو و عقب حرکت می‌کند. نمودار زیر، مکان افقی حیوان را برحسب متر نسبت به زمان نشان می‌دهد.

1. جابجایی حیوان بین زمان‌های صفر و ۵ ثانیه، چه مقدار است؟
2. مسافت طی شده توسط حیوان بین زمان‌های صفر و ۵ ثانیه، چه مقدار است؟

پاسخ

جابجایی برابر تفاضل مکان نهایی و مکان اولیه جسم است. بنابراین، به صورت زیر به‌دست می‌آید:

$$\triangle x = x_ f - x_ i$$

در این مثال، جابجایی حیوان بین زمان‌های صفر و پنج ثانیه خواسته شده است. بنابراین، مکان اولیه حیوان در زمان صفر، برابر ۲- متر و مکان نهایی آن، در زمان پنج ثانیه،برابر ۶ متر خواهد بود. در نتیجه، جابجایی حیوان برابر است با:

$$\triangle x = x ( 5 s ) - x ( 0) = 6 m - ( - 2 m ) = 8 m$$

در ادامه، مسافت طی شده توسط حیوان را در بازه زمانی مشابه به‌دست می‌آوریم. برای انجام این کار، به نمودار مکان زمان دقت کنید. حرکت حیوان، با توجه به این نمودار، به سه بخش تقسیم می‌شود:

1. بخش اول حرکت بین زمان‌های صفر تا ۳ ثانیه رخ می‌دهد. نمودار در این بخش، خطی مستقیمی با شیب ثابت و مثبت است. بنابراین، حیوان از مکان ۲- متر، با سرعت مثبت، شروع به حرکت می‌کند و پس از ۳ ثانیه به مکان ۶+ متر می‌رسد. مسافت طی شده در این زمان، برابر ۸ متر خواهد بود.
2. بخش دوم حرکت بین زمان‌های ۳ تا ۵ ثانیه رخ می‌دهد. نمودار در این بخش، خطی افقی با شیب صفر است. در نتیجه، حیوان پس از ۸ متر، به مدت دو ثانیه استراحت می‌کند.
3. بخش سوم حرکت بین زمان‌های ۵ تا ۶ ثانیه رخ می‌دهد. نمودار در این بخش، خطی مستقیم با شیب ثابت و منفی است. بنابراین، حیوان از مکان ۶+ متر، با سرعت منفی، شروع به حرکت می‌کند و پس از یک ثانیه به مکان صفر متر می‌رسد. مسافت طی شده در این زمان، برابر ۶ متر خواهد بود.

از آنجا که مسافت طی شده در ۵ ثانیه اول حرکت خواسته شده است، دو بخش اول حرکت را باید در نظر بگیریم. مسافت طی شده توسط حیوان در این بازه زمانی برابر ۸ متر خواهد بود.

مثال نهم حرکت یکنواخت

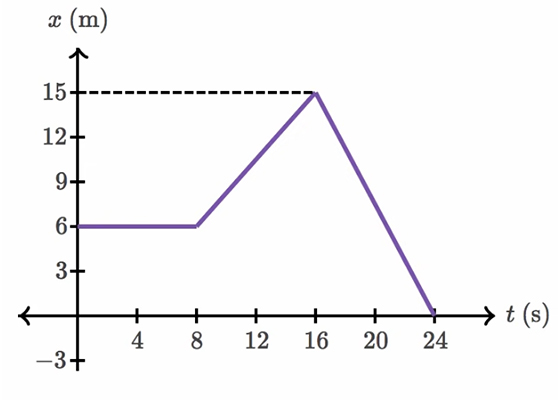
گورکنی به وزن ۲/۷ کیلوگرم روی خط مستقیمی حرکت می‌کند. نمودار مکان زمان حرکت او به صورت زیر نشان داده شده است. جابجایی و مسافت گورکن را در کل مسیر حرکت به‌دست آورید.

پاسخ

برای به‌دست آوردن مسافت و جابجایی گورکن در کل مسیر، ابتدا باید ببینیم حرکت به چند بخش تقسیم می‌شود. با توجه به نمودار نشان داده شده در بالا، حرکت از سه بخش تشکیل شده است:

1. نمودار مکان زمان در ۸ ثانیه اول حرکت، خطی افقی با شیب صفر است. بنابراین، گورکن در این مدت در مکان خود، بدون حرکت ایستاده است.
2. بخش دوم حرکت بین زمان‌های ۸ تا ۱۶ ثانیه رخ می‌دهد. نمودار در این بخش، خطی مستقیم با شیب ثابت و مثبت است. بنابراین، گورکن از مکان ۶ متر، با سرعت مثبت، شروع به حرکت می‌کند و پس از ۸ ثانیه به مکان ۱۵ متر می‌رسد.
3. بخش سوم حرکت بین زمان‌های ۱۶ تا ۲۴ ثانیه رخ می‌دهد. نمودار در این بخش، خطی مستقیم با شیب ثابت و منفی است. بنابراین، گورکن از مکان ۱۵ متر، با سرعت منفی، شروع به حرکت می‌کند و پس از ۸ ثانیه به مکان اولیه خود می‌رسد.

جابجایی در کل مسیر برابر تفاضل مکان اولیه و مکان نهایی است:

$$\triangle x = x_ f - x_ i = 0 - 6 m = - 6 m$$

برای به‌دست آوردن مسافت کل، مسافت طی شده در هر بخش را با یکدیگر جمع می‌کنیم. مسافت طی شده توسط گورکن در ۸ ثانیه اول حرکت برابر صفر، در ۸ ثانیه دوم حرکت، برابر ۹ متر و در ۸ ثانیه سوم حرکت، برابر ۱۵ متر است. بنابراین، مسافت کل برابر ۲۴ متر خواهد بود.

مثال دهم حرکت یکنواخت

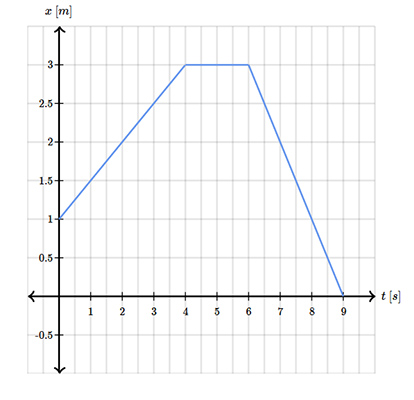
پنگوئن گرسنه‌ای برای یافتن غذا، به صورت افقی به چپ و راست حرکت می‌کند. نمودار مکان او برحسب زمان به صورت زیر نشان داده شده است. سرعت لحظه‌ای پنگوئن در زمان‌های ۲، ۵ و ۸ ثانیه را به‌دست آورید.

پاسخ

ابتدا، سرعت لحظه‌ای را در زمان ۲ ثانیه به‌دست می‌آوریم. برای انجام این کار تنها کافی است شتاب نمودار را در زمان دو ثانیه محاسبه کنیم.

$$m = \frac { x _ 2 - x_ 1 } { t _ 2 - t _ 1 }$$

برای به‌دست آوردن شیب خط، دو نقطه دلخواه را روی خط انتخاب می‌کنیم. برای راحتی کار، دو نقطه به گونه‌ای انتخاب می‌شوند که خواندن مختصات آن‌ها کلر ساده‌ای باشد. با انتخاب دو نقطه $$(0 s \, 1 m )$$ و $$( 4 s \, 3 m )$$ و قرار دادن آن‌ها در رابطه شیب داریم:

$$m = \frac { 3 m - 1 m } { 4 s - 0 s } = \frac { 2 m } { 4 s} = \frac { 1 } {2 } \frac { m } { s}$$

بنابراین، سرعت پنگوئن در ثانیه دوم برابر ۰/۵ متر بر ثانیه است.

در ادامه، سرعت پنگوئن را در زمان ۵ ثانیه به‌دست می‌آوریم. نمودار مکان زمان در این لحظه، خطی افقی با شیب صفر است. در نتیجه، سرعت پنگوئن در زمان ۵ ثانیه برابر صفر خواهد بود. سرعت پنگوئن در زمان ۸ ثانیه، منفی است. زیرا، نمودار مکان زمان در این لحظه خطی مستقیم با شیب قابت و منفی خواهد بود. برای به‌دست آوردن سرعت در این زمان، دو نقطه در ابتدا و انتهای خط را انتخاب می‌کنیم: $$( 6 s \, 3 m ) \, ( 9 s \, 0 m)$$.

$$m = \frac { 0 m - 3 m } { 9 s - 6 s } = \frac { - 3 m } { 3 s} = - 1 \frac { m } { s}$$

مثال یازدهم حرکت یکنواخت

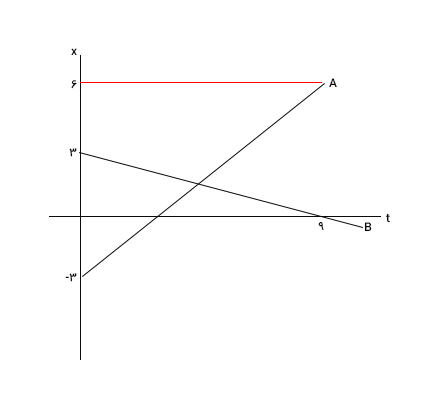
نمودارهای مکان زمان دو جسم A و B در تصویر زیر، در یک دستگاه مختصات نشان داده شده است.

1. دو جسم در چه زمانی به یکدیگر می‌رسند؟
2. فاصله دو جسم از یکدیگر در لحظه تغییر جهت بردار مکان جسم A، چند متر است؟

پاسخ

در ابتدا، قسمت ۱ مثال را حل می‌کنیم. برای حل مثال‌های دو جسمی یا بیشتر، ابتدا معادله حرکت هر جسم را به‌دست می‌آوریم. نمودار مکان زمان جسم A، خطی مستقیم با شیب مثبت است. بنابراین جسم A با سرعت ثابت و مثبت حرکت می‌کند و سرعت آن برابر است با:

$$V_ A = \frac { 6 m - ( - 3 m) } { 9 s - 0 s } = \frac {9 m } { 9 s} = 1 \frac { m } { s}$$

از آنجا که معادله مکان زمان در حرکت با سرعت ثابت به صورت $$x = vt + x_ 0$$ نوشته می‌شود، معادله مکان زمان جسم A برابر $$x_ A = t - 3$$ خواهد بود.

نمودار مکان زمان جسم B، خطی مستقیم با شیب منفی است. بنابراین جسم B با سرعت ثابت و منفی حرکت می‌کند و سرعت آن برابر است با:

$$V_ B = \frac {0 m - 3 m) } { 9 s - 0 s } = \frac {- 3 m } { 9 s} =- \frac{1} {3} \frac { m } { s}$$

از آنجا که معادله مکان زمان در حرکت با سرعت ثابت به صورت $$x = vt + x_ 0$$ نوشته می‌شود، معادله مکان زمان جسم B برابر $$x_ B = - \frac {1} { 3} t + 3$$ خواهد بود.

هنگامی که دو جسم به یکدیگر می‌رسند، مکان‌های آن‌ها با یکدیگر برابر خواهد بود:

$$x_ A = x _ B t - 3 = - \frac {1} { 3 } t + 3 \Rightarrow t + \frac { 1} { 3 } t = 6 \Rightarrow \frac { 4} { 3} t = 6 t = \frac { 6 } { \frac { 4 } { 3 }} = 6 \times \frac { 3 } {4 } = 4.5 s$$

قسمت ۲: ابتدا باید بدانیم، بردار مکان جسم A در چه لحظه‌ای تغییر جهت می‌دهد. جسم A از مکان ۳- متر در زمان صفر شروع به حرکت می‌کند و پس از رسیدن به مکان صفر، در راستای مثبت به حرکت خود ادامه می‌دهد. بنابراین، بردار مکان A پس از رسیدن آن به مکان صفر، تغییر جهت خواهد داد. برای به‌دست آوردن زمان این تغییر جهت، معادله مکان زمان جسم A را برابر صفر قرار می‌دهیم:

$$x_ A = 0 \Rightarrow t - 3 = 0 \Rightarrow t = 3 s$$

مکان جسم B در زمان ۳ ثانیه برابر است با:

$$x_ B = - \frac {1} { 3} t + 3 \Rightarrow x _ B ( 3 s ) = - \frac {1} { 3} \times 3 + 3 = 2 m$$

در نتیجه، در لحظه تغییر جهت بردار مکان A، فاصله دو جسم برابر ۲ متر خواهد بود.

پرسش: با توجه به نمودار مکان زمان داده شده در پرسش بالا، سرعت و تندی متوسط اتومبیل در کل مسیر حرکت، چه مقدار است؟

پاسخ: از آنجا که اتومبیل پس از ۵ ساعت، به نقطه آغاز حرکت بازمی‌گردد، جابجایی و در نتیجه، سرعت متوسط آن در کل مسیر برابر صفر است. برای به‌دست آوردن تندی متوسط در کل مسیر، باید مسافت کل را به‌دست آوریم. با توجه به پاسخ پرسش می‌دانیم حرکت اتومبیل به ۴ مرحله تقسیم می‌شود. مسافت طی شده توسط اتومبیل در مرحله A برابر ۴۰ کیلومتر، در مرحله B برابر صفر کیلومتر، در مرحله C برابر ۴۰ کیلومتر و در مرحله D برابر ۸۰ کیلومتر است. در نتیجه، مسافت کل برابر ۱۶۰ کیلومتر و تندی متوسط برابر $$s_ {avg} = \frac { 160 km } { 5 h } = 32 \frac { km } { h}$$ خواهد بود.

نمودار مکان زمان برای حرکت با شتاب ثابت

شتاب به صورت تغییرات سرعت برحسب زمان تعریف می‌شود. همچنین، سرعت برابر تغییرات مکان نسبت به زمان (مشتق مکان نسبت به زمان) است. بنابراین، شتاب را می‌توان به صورت $$a = \frac{\text{d}^ 2 x}{\text{d}t ^ 2}$$ نوشت. اگر شتاب حرکت جسمی، ثابت باشد:

$$a = \frac{\text{d}^ 2 x}{\text{d}t ^ 2} = C$$

برای به‌دست آوردن معادله مکان نسبت به زمان، از طرفین رابطه بالا انتگرال می‌گیریم:

$$\int a dt = \int \frac{\text{d}^ 2 x}{\text{d}t ^ 2} dt = \int C dt \int \frac{\text{d}v}{\text{d}t} dt = \int C dt v ( t) = C t + C_1$$

به این نکته توجه داشته باشید که سرعت، برابر مشتق مکان نسبت به زمان و شتاب برابر مشتق سرعت نسبت به زمان یا مشتق دوم مکان نسبت به زمان است. از طرفین $$v ( t ) = Ct + C_1$$ بار دیگر انتگرال می‌گیریم:

$$\int v ( t) dt = \int (C t + C_1 ) dt \int \frac{\text{d}x}{\text{d}t} dt = \int (C t + C_1 ) dt x ( t ) = \frac { 1} { 2} C t ^ 2 + C _1 t + C_2$$

در رابطه بالا، $$C$$ و $$C_1$$ و $$C_ 2$$ ثابت‌های انتگرال‌گیری هستند. معادله $$x( t)$$، معادله درجه دو برحسب زمان یا نموداری به شکل سهمی است. در نتیجه، نمودار مکان زمان در حرکت با شتاب ثابت، نموداری سهمی شکل با تقعر رو به بالا یا رو به پایین خواهد بود.

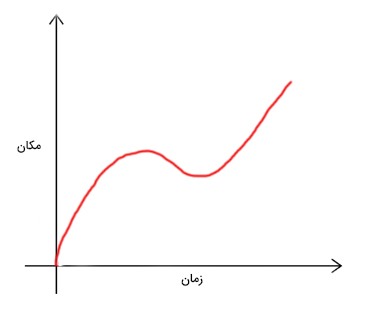
نمودار مکان زمان برای حرکت با شتاب متغیر

در حرکت با شتاب متغیر، شتاب جسم نسبت به زمان تغییر می‌کند. به بیان دیگر، مشتق دوم مکان نسبت به زمان، مخالف صفر است و نسبت به زمان تغییر می‌کند.

مثال اول حرکت شتاب‌دار

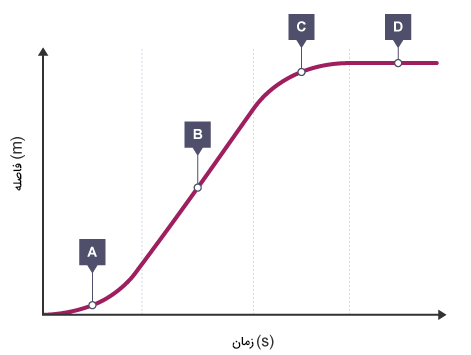
نمودار مکان زمان جسمی در تصویر زیر نشان داده شده است. حرکت جسم در هر یک از بخش‌های A و B و C و D را توصیف کنید.

پاسخ

شیب نمودار مکان زمان در قسمت A، افزایشی است. بنابراین سرعت جسم در این قسمت افزایش می‌یابد. از آنجا که تقعر منحنی رو به بالا است، جسم با شتاب مثبت حرکت می‌کند. نمودار در قسمت B، خطی با شیب مثبت و ثابت است. در نتیجه، جسم در این قسم با سرعت ثابت و مثبت به حرکت خود ادامه می‌دهد. شیب خط مماس بر نمودار مکان زمان در قسمت C، کاهش می‌یابد و به صفر نزدیک می‌شود. از این‌رو، جسم در این قسمت با سرعت ثابت و مثبت به حرکت خود ادامه می‌دهد. همچنین، تقعر منحنی در قسم C به سمت پایین و شیب حرکت منفی است. در قسمت D، نمودار، خطی افقی با شیب صفر است. در نتیجه، جسم پس از حرکت با سرعت کاهشی در قسمت C، در قسمت D به طور کامل متوقف می‌شود.

نکته: هرچه شیب خط در نمودار مکان زمان بیشتر باشد، جسم با سرعت بیشتری حرکت می‌کند.

مثال دوم حرکت شتاب‌دار

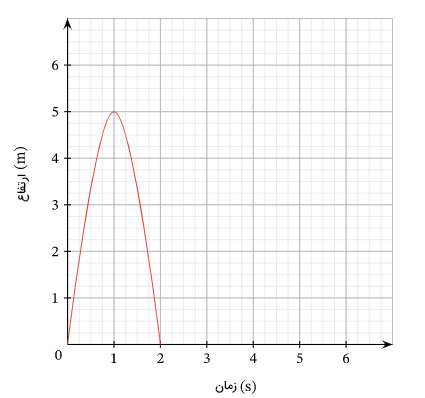
توپی را به صورت عمودی به سمت بالا پرتاب می‌کنیم. توپ پس از رسیدن به ارتفاعی بیشینه به سمت زمین حرکت می‌کند. نمودار مکان زمان توپ در تصویر زیر نشان داده شده است.

1. ارتفاع بیشینه توپ را به‌دست آورید.
2. در چه زمانی توپ به ارتفاع بیشینه خود می‌رسد.

پاسخ

در حرکت توپ به سمت بالا، جهت مثبت را به سمت بالا انتخاب می‌کنیم. بنابراین، هنگامی که توپ به سمت بالا حرکت می‌کند، سرعت آن مثبت است، اما اندازه آن کاهش می‌یابد و به صفر می‌رسد. بنابراین، شتاب حرکت منفی است. توپ پس از رسیدن به ارتفاع بیشینه، تغییر جهت می‌دهد و به سمت زمین حرکت می‌کند. از آنجا که جهت حرکت توپ به سمت پایین است، سرعت آن منفی خواهد بود.

برای به‌دست آوردن ارتفاع بیشینه، به نمودار مکان زمان دقت می‌کنیم. نمودار، سهمی با تقعر رو به پایین و بیشینه‌ای در نقطه $$(1 \, 4)$$است. بنابراین، توپ یک ثانیه پس از پرتاب به ارتفاع بیشینه ۴ متر از سطح زمین می‌رسد.

مثال سوم حرکت شتاب‌دار

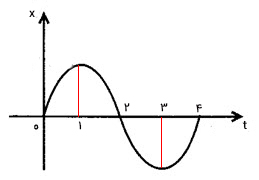
نمودار مکان زمان جسمی به صورت زیر داده شده است. کدام یک از عبارت‌های زیر صحیح است؟

1. سرعت جسم در بازه زمانی صفر تا دو ثانیه، مثبت است.
2. سرعت ذره تنها در بازه زمانی ۳ تا ۴ ثانیه، مثبت است.
3. سرعت ذره در بازه زمانی یک تا ۳ ثانیه مثبت است.
4. سرعت ذره در بازه زمانی صفر تا یک ثانیه، مثبت است.
5. سرعت ذره در بازه زمانی صفر تا یک ثانیه و ۳ تا ۴ ثانیه مثبت است.

پاسخ

همان‌طور که در مطالب بالا گفته شد، شیب خط مماس بر نمودار مکان زمان، سرعت جسم را به ما می‌دهد. بنابراین، برای آن‌که بدانیم سرعت ذره در چه زمان‌هایی مثبت و در چه زمان‌هایی منفی است، خط مماس بر آن را در زمان‌های مختلف رسم می‌کنیم.

بازه زمانی صفر تا یک ثانیه: شیب خط مماس بر نمودار مکان زمان در این بازه زمانی و در نتیجه، سرعت حرکت جسم، مثبت است. اما اندازه سرعت کاهش می‌یابد و در زمان یک ثانیه به صفر می‌رسد. بنابراین، شتاب حرکت منفی خواهد بود.

بازه زمانی یک تا دو ثانیه: شیب خط مماس بر نمودار مکان زمان در این بازه زمانی و در نتیجه، سرعت حرکت جسم، منفی است. منفی بودن سرعت بدان معنا است که جسم در جهت مخالف جهت مثبت شروع به حرکت می‌کند و پس از یک ثانیه به نقطه آغاز حرکت می‌رسد. توجه به این نکته مهم است که مقدار سرعت در جهت منفی زیاد می‌شود. بنابراین، شتاب حرکت ذره همچنان منفی است.

بازه زمانی ۲ تا ۳ ثانیه: شیب خط مماس بر نمودار مکان زمان در این بازه زمانی و در نتیجه، سرعت حرکت جسم، همچنان منفی است. در زمان سه ثانیه، سرعت حرکت جسم به صفر می‌رسد، بنابراین شتاب حرکت جسم، مثبت خواهد بود.

بازه زمانی ۳ تا ۴ ثانیه: شیب خط مماس بر نمودار مکان زمان در این بازه زمانی و در نتیجه، سرعت حرکت جسم، مثبت است. در این قسمت جهت حرکت جسم تغییر می‌کند و به سمت نقطه آغاز، حرکت می‌کند و در زمان ۴ ثانیه به آن می‌رسد. از آنجا که اندازه سرعت از صفر، افزایش می‌یابد، شتاب حرکت جسم مثبت خواهد بود.

با توجه به توضیحات داده شده، پاسخ صحیح گزینه ۵ است.

مثال چهارم مکان زمان برای حرکت شتاب‌دار

نمودار مکان زمان نشان داده شده در تصویر زیر مربوط به توپ تنیسی است که به صورت عمودی توسط بازیکنی به هوا پرتاب می‌شود و پس از مدت زمان مشخصی به سمت زمین برمی‌گردد.

1. نمودار مکان زمان توپ را توصیف کنید.
2. شتاب توپ در چه زمانی مثبت و در چه زمانی منفی است؟
3. آیا سرعت توپ در طول حرکت صفر می‌شود؟

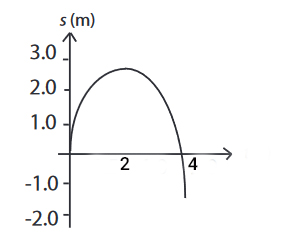
پاسخ

ابتدا فرض می‌کنیم جهت حرکت مثبت به سمت بالا است. هنگام پرتاب توپ به صورت عمودی به سمت بالا، دو اتفاق رخ می‌دهد:

• توپ با سرعت مثبت به سمت بالا حرکت می‌کند و پس از مدت زمان مشخصی به بیشینه ارتفاع خود می‌رسد.
• توپ با سرعت منفی به سمت زمین حرکت می‌کند و پس از مدت زمان مشخصی به سطح زمین می‌رسد.

قسمت ۱: بازیکن توپ را به صورت عمودی به سمت بالا پرتاب می‌کند. با توجه به نمودار نشان داده شده در بالا، دست بازیکن را که ارتفاع مشخصی از سطح زمین دارد، مبدأ مختصات در نظر می‌گیریم. شیب خط مماس بر نمودار مکان زمان در مبدأ، مثبت است. بنابراین، توپ با سرعت مثبت به سمت بالا شروع به حرکت می‌کند و دو ثانیه پس از پرتاب شدن به ارتفاع بیشینه از سطح زمین می‌رسد. شیب خط مماس بر نمودار مکان زمان در این نقطه، صفر است. در نتیجه، همان‌طور که انتظار می‌رود سرعت توپ در ارتفاع بیشینه برابر صفر خواهد بود و با تغییر جهت حرکت، به سمت زمین برمی‌گردد.

پس از زمان دو ثانیه، شیب خط مماس بر نمودار، منفی است. در نتیجه، سرعت توپ به هنگام بازگشت، منفی خواهد بود. در ثانیه چهارم حرکت، توپ به مبدأ مکان (دست بازیکن) می‌رسد و با عبور از آن (مکان منفی) به زمین می‌رسد.

قسمت ۲:‌ در این قسمت، زمان‌هایی که شتاب توپ، منفی و زمان‌هایی که شتاب آن، مثبت است را به‌دست می‌آوریم. تقعر منحنی مکان زمان، رو به پایین است و یک بیشینه دارد. بنابراین، شتاب حرکت در کل زمان، منفی است. به هنگام بالا رفتن توپ، سرعت مثبت و شتاب منفی است. از این‌رو، از مقدار سرعت حرکت کاسته می‌شود و در نقطه بیشینه سرعت به صفر می‌رسد. در مرحله دوم حرکت و به هنگام پایین آمدن توپ، سرعت و شتاب هم‌راستا و منفی هستند، بنابراین اندازه شتاب، در راستای منفی زیاد می‌شود.

قسمت ۳: سرعت حرکت، همان‌طور که در توضیحات بالا، گفته شد در زمان دو ثانیه برابر صفر می‌شود و پس از آن جهت حرکت، تغییر می‌کند.

نکته: نمودار مکان زمان در حرکت با شتاب ثابت، سهمی با تقعر رو به بالا یا رو به پایین است. چرا؟ معادله مکان برحسب زمان در حرکت با شتاب ثابت برابر است با:

$$x = \frac { 1} { 2 } a t ^ 2 + v_ 0 t + x_ 0$$

معادله فوق، معادله سهمی است. اگر شتاب حرکت مثبت باشد، تقعر سهمی به سمت بالا و اگر شتاب حرکت منفی باشد، تقعر سهمی به سمت پایین خواهد بود.

مثال پنجم حرکت شتاب‌دار

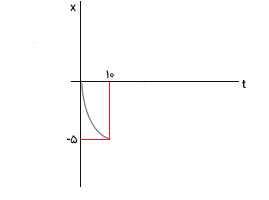
نمودار مکان زمان جسمی که با شتاب ثابت حرکت می‌کند، به صورت بخشی از یک سهمی، در تصویر زیر نشان داده شده است. شتاب و سرعت اولیه حرکت جسم را به‌دست آورید.

پاسخ

جسم با شتاب ثابت حرکت می‌کند، بنابراین نمودار مکان زمان آن به صورت سهمی است. همچنین،‌ معادله مکان برحسب زمان جسم در حرکت با شتاب ثابت به صورت زیر نوشته می‌شود:

$$x = \frac { 1} { 2 } a t ^ 2 + v- 0 t + x_ 0$$

مکان اولیه جسم در زمان صفر، برابر صفر است. بنابراین، مقدار $$x_ 0$$ برابر صفر خواهد بود. همچنین، نقطه $$(10 s \, - 5 m)$$ نقطه کمینه منحنی است. شیب یا مشتق منحنی در این نقطه برابر صفر خواهد بود. از این‌رو، ابتدا مشتق x برحسب زمان را به‌دست می‌آوریم و مقدار آن را در زمان ۱۰ ثانیه برابر صفر قرار می‌دهیم.

$$\frac{\text{d}x}{\text{d}t} ( t = 10 s) = 0 \frac{\text{d}}{\text{d}t} ( \frac { 1} { 2 } a t ^ 2 + v_ o t ) = at+ v_ 0 10 a + v_ 0 = 0$$

برای آن‌که شتاب و سرعت اولیه را به‌دست آوریم به معادله دیگری برحسب این دو کمیت نیاز داریم. با توجه به نمودار مکان زمان، مکان جسم در زمان ۱۰ ثانیه، برابر ۵- متر است. بنابراین، به جای t و x در معادله مکان برحسب زمان، این دو مقدار را قرار می‌دهیم:

$$x = \frac { 1} { 2 } a t ^ 2 + v- 0 t + x_ 0 -5 = \frac { 1} { 2 } \times 10 a + 10 v_ 0 -5 = 5 a + 10 v_ 0 -1 = a + 2 v_ 0$$

دو معادله و دو مجهول داریم. با حل آن‌ها به جواب‌های ۰/۰۵ متر بر مجذور ثانیه برای شتاب و ۰/۵- متر بر ثانیه برای سرعت اولیه می‌رسیم.

مثال ششم حرکت شتاب‌دار

نمودار مکان زمان جسمی به صورت سهمی است. سرعت اولیه و شتاب آن را به‌دست آورید.

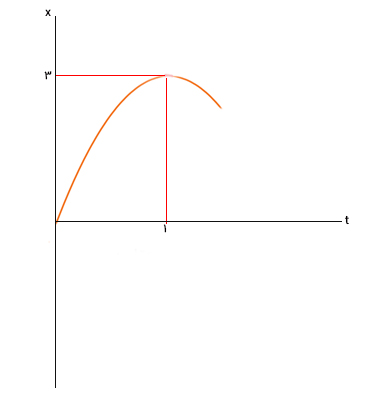
پاسخ

از آنجا که منحنی مکان زمان به صورت سهمی است، جسم با شتاب ثابت حرکت می‌کند. برای به‌دست آوردن سرعت اولیه و شتاب، فرض‌های زیر را در نظر می‌گیریم:

• مکان اولیه جسم در زمان صفر برابر صفر است. بنابراین مقدار $$x_ 0$$، صفر خواهد بود.
• سرعت جسم یا مشتق مکان نسبت به زمان در زمان یک ثانیه، برابر صفر است.
• چسم، یک ثانیه پس از شروع حرکت در فاصله ۳ متری از مبدأ قرار دارد.

نقطه $$(1 s \, -3 m)$$ نقطه بیشینه منحنی است. شیب یا مشتق منحنی در این نقطه برابر صفر خواهد بود. از این‌رو، ابتدا مشتق x برحسب زمان را به‌دست می‌آوریم و مقدار آن را در زمان یک ثانیه برابر صفر قرار می‌دهیم.

$$\frac{\text{d}x}{\text{d}t} ( t = 1 s) = 0 \frac{\text{d}}{\text{d}t} ( \frac { 1} { 2 } a t ^ 2 + v_ o t ) = at+ v_ 0 a + v_ 0 = 0$$

برای آن‌که شتاب و سرعت اولیه را به‌دست آوریم به معادله دیگری برحسب این دو کمیت نیاز داریم. با توجه به نمودار مکان زمان، مکان جسم در زمان یک ثانیه، برابر ۳ متر است. بنابراین، به جای t و x در معادله مکان برحسب زمان، این دو مقدار را قرار می‌دهیم:

$$x = \frac { 1} { 2 } a t ^ 2 + v- 0 t + x_ 0 3 = \frac { 1} { 2 } \times 1 \times a + v_ 0 3 = \frac { 1} { 2 } a + v_ 0$$

دو معادله و دو مجهول داریم. با حل آن‌ها به جواب‌های ۶- متر بر مجذور ثانیه برای شتاب و ۶ متر بر ثانیه برای سرعت اولیه می‌رسیم.

مثال هفتم حرکت شتاب‌دار

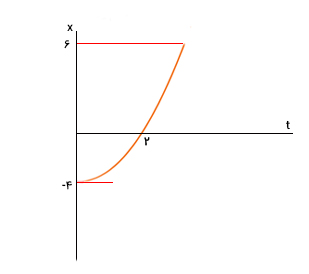
نمودار مکان زمان جسمی به صورت سهمی در تصویر زیر نشان داده شده است. سرعت جسم به هنگام عبور از مبدأ مکان را به‌دست آورید.

پاسخ

از آنجا که منحنی مکان زمان به صورت سهمی است، جسم با شتاب ثابت حرکت می‌کند. برای به‌دست آوردن سرعت جسم به هنگام عبور از مبدأ، ابتدا باید معادله مکان برحسب زمان را به‌دست آوریم. برای به‌دست آوردن معادله $$x-t$$ فرض‌های زیر را در نظر می‌گیریم:

• مکان اولیه جسم در زمان صفر برابر ۴- متر است. بنابراین مقدار $$x_ 0$$ برابر ۴- متر خواهد بود.
• مکان جسم ۲ ثانیه پس از شروع حرکت برابر ۶ متر است.
• شیب نمودار مکان زمان در لحظه صفر، برابر صفر است.

از آنجا که نمودار مکان زمان در حرکت با شتاب ثابت، سهمی است، معادله مکان برحسب زمان به صورت زیر نوشته می‌شود:

$$x = \frac {1 } {2 } a t ^ 2 + v _ 0 t + x_ 0$$

بر طبق نمودار نشان داده شده در بالا، $$x_ 0$$ برابر ۴- متر است:

$$x = \frac {1 } {2 } a t ^ 2 + v _ 0 t - 4$$

بر طبق فرض دوم، جسم ۲ ثانیه پس از شروع حرکت به ۶ متری مبدأ می‌رسد، بانابراین به جای t مقدار ۲ را در معادله مکان زمان قرار می‌دهیم:

$$6 = \frac {1 } {2 } a (2) ^ 2 + v _ 0 \times 2 - 4 6 = 2 a +2 v_0 -4 10 = 2 a + 2 v_ 0 5 = a + v_ 0$$

همچنین، شیب نمودار در لحظه صفر، برابر صفر است. یعنی جسم از حالت سکون شروع به حرکت می‌کند. در نتیجه، معادله مکان زمان به صورت زیر نوشته می‌شود:

$$x = \frac { 5} {2} t ^ 2 - 4$$

از معادله مکان برحسب زمان مشتق می‌گیریم و رابطه سرعت برحسب زمان را به‌دست می‌آوریم:

$$v = 5t$$

از آنجا که جسم در زمان ۲ ثانیه از مبدأ می‌گذرد، سرعت آن در این لحظه برابر ۱۰ متر بر ثانیه خواهد بود.

پرسش های رایج در مورد نمودار مکان زمان

تا اینجا می‌دانیم نمودار مکان زمان چیست و چه اهمیتی در توصیف حرکت اجسام متحرک دارد. در ادامه، به چند پرسش مهم در مورد این نمودار پاسخ می‌دهیم.

نمودار مکان زمان در حرکت با سرعت ثابت چگونه است؟

نمودار مکان زمانِ جسمی که با سرعت ثابت حرکت می‌کند به صورت خط مستقیمی با شیب مثبت یا منفی است.

نمودار مکان زمان در حرکت با شتاب ثابت چگونه است؟

نمودار مکان زمانِ جسمی که با شتاب ثابت حرکت می‌کند سهمی با تقعر رو به بالا یا پایین است.

شیب نمودار مکان زمان چه کمیتی را نشان می‌ دهد؟

شیب خط مماس بر نمودار مکان زمان در هر لحظه از زمان، سرعت لحظه‌ای و شیب خط متصل‌کننده دو نقطه در بازه زمانی مشخص، سرعت متوسط را نشان می‌دهد.

چگونه می توان با استفاده از نمودار مکان زمان در حرکت با شتاب ثابت، علامت شتاب و نوع حرکت را مشخص کرد؟

در مطالب بالا گفتیم، نمودار مکان زمان در حرکت با شتاب ثابت، سهمی با تقعر رو به بالا یا پایین است. اگر سهمی دارای نقطه بیشینه باشد، علامت سرعت از مثبت به منفی تغییر می‌کند. بنابراین، علامت شتاب منفی خواهد بود. در مقابل، اگر سهمی دارای نقطه کمینه باشد، علامت سرعت از منفی به مثبت تغییر می‌کند. در نتیجه، علامت شتاب مثبت است.

جمع‌بندی

در این مطلب، نمودار مکان زمان را به زبان ساده توضیح می‌دهیم. پس از خواندن این مطلب، می‌دانیم:

• نمودار مکان زمان چیست و چه اطلاعاتی را می‌توان از آن به‌دست آورد.
• شیب خط مماس بر نمودار مکان زمان در هر لحظه از زمان، سرعت لحظه‌ای جسم را در آن زمان به ما می‌دهد.
• نمودار مکان زمان برای حرکت با سرعت ثابت چگونه رسم می‌شود.
• نمودار مکان زمان برای حرکت با شتاب ثابت چگونه رسم می‌شود.