نسبت های مساوی چیست؟ – ریاضی به زبان ساده + حل تمرین و مثال
در آموزشهای پیشین مجله فرادرس، با نسبت در ریاضی و درصد آشنا شدیم. در این آموزش، میخواهیم ببینیم نسبت های مساوی چه هستند و چه ویژگیهایی دارند.
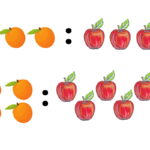
مثال ساده نسبت
مارال میخواهد تعدادی شیرینی بپزد. او دستورالعملهای پخت کلوچه را مطالعه میکند. اکثر دستورالعملها میگویند که برای یک تعداد مشخص کلوچه (مثلاً یک جعبه)، او باید از ۳ فنجان آرد، ۱ فنجان کره، ۱ فنجان شکر و برخی مواد اولیه دیگر استفاده کند. او همراه با برادرش برای خرید آرد و کره به فروشگاه میرود. در هنگام خرید، این پرسش در ذهن مارال ایجاد میشود که نسبت آرد به کره در یک تعداد دلخواه دیگر (چند جعبه) از کلوچهها چقدر است؟ اگر او بخواهد ۳ جعبه کلوچه درست کند، به چه مقدار آرد و کره نیاز دارد؟ این پرسش مارال همان چیزی است که به مفهوم نسبت های مساوی برمیگردد. در ادامه، نحوه نوشتن نسبتها و یافتن نسبت های مساوی را یاد خواهیم گرفت.

نوشتن نسبت ها
نسبت، مقایسه دو کمیت از طریق تقسیم است. نسبتها یک مقایسه جزء به جزء یا مقایسه جزء به کل را توصیف میکنند، بدین معنی که جزئی از چیزی را با جزئی دیگر از همان چیز مقایسه میکنند، مثلاً مقایسه تعداد سیبها با پرتقالها در که هردو جزئی از همه میوهها هستند. یا نسبت تعداد سیبها به کل میوهها مثالی از مقایسه جزء به کل است. نسبتها را میتوان به سه شکل نمایش داد: بهصورت کسری، با دو نقطه و با کلمه "به". بهطور دقیقتر، نسبت مقدار به مقدار را میتوان به شکلهای زیر نوشت:
به
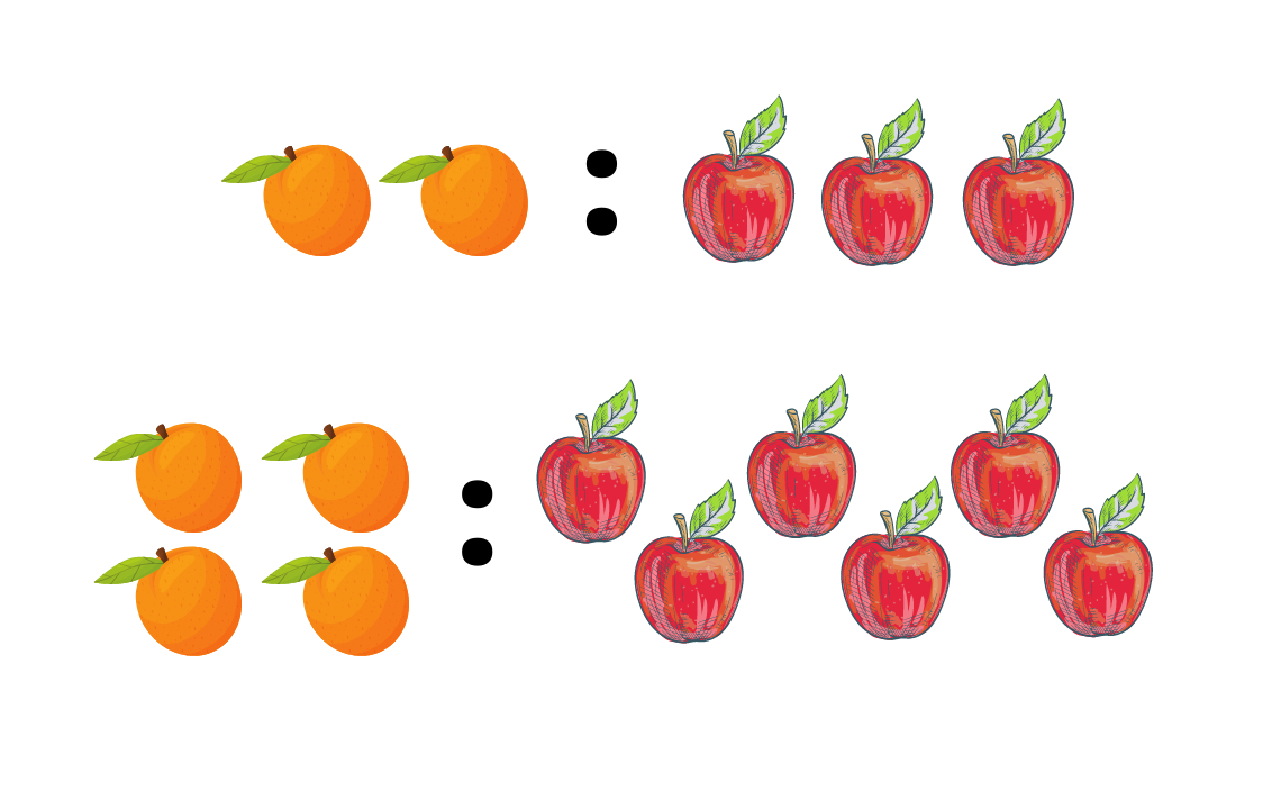
به تصویر زیر دقت کنید.

در این تصویر سه ستاره و دو دایره وجود دارد. نسبتی که مقایسه تعداد ستارهها به تعداد دایرهها را توصیف می کند، نسبت جزء به جزء است. همچنین، نسبتی که تعداد ستارهها را به تعداد کل شکلها توصیف میکند، نسبت جزء به کل است.
برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد میکنیم به مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلمهای آموزشهای دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
اکنون میخواهیم نسبتی برای تعداد ستارهها به تعداد دایرهها به سه روش مختلف بنویسیم. هنگام نوشتن یک نسبت، ترتیب اعداد مهم است. عدد اول باید با کمیت اول و عدد دوم با کمیت دوم مطابقت داشته باشد. همانطور که میبینیم، ۳ ستاره داریم و دو دایره. بنابراین، نسبت تعداد ستارههابه دایرهها بهشکل زیر است:
۳ به ۲
نسبت 3 به 2 به ما میگوید که برای هر 2 دایره 3 ستاره وجود دارد. برخی از نمونههای دیگر نسبتهای جزء به جزء برای این تصویر میتوانند نسبتهایی باشند که اجسام نارنجی را به اجسام آبی، ستارههای آبی به ستارههای نارنجی، دایرههای نارنجی به ستارههای آبی و بسیاری دیگر را توصیف میکنند.
اکنون یک نسبت جزء به کل مینویسیم که تعداد شکلهای آبی به تعداد کل شکلها را توصیف میکند. همانطور که در تصویر مشخص است، یک شکل آبی دارم و کل شکلها نیز ۵ تا هستند. نسبت را به سه روش مختلف مینویسیم:
۱ به ۵
محاسبه نسبت های مساوی
دو نسبتی که دارای مقدار یکسانی هستند نسبت معادل یا نسبت مساوی نام دارند. برای یافتن یک نسبت معادل، هر دو کمیت را در یک عدد ضرب یا تقسیم میکنیم. این همان فرایند یافتن کسرهای مساوی است.
برای مثال، نسبت را در نظر بگیرید که نسبت تعداد ستارهها به تعداد دایرهها را نشان میدهد. صورت و مخرج را در 2 ضرب میکنیم:
نسبت مساوی نسبت است. تصویر 3 ستاره و 2 دایره و تصویر 6 ستاره و 4 دایره را با هم مقایسه کنید. در هر دو تصویر 3 ستاره بهازای هر 2 دایره وجود دارد.

در ابتدای آموزش گفتیم که مارال به فروشگاه رفته تا مواد اولیه کلوچه را بخرد. در دستور پخت از 3 فنجان آرد و 1 فنجان کره استفاده میشود و او میخواهد 3 جعبه کلوچه بپزد. او برای اینکه بفهمد به چه مقدار آرد و کره نیاز دارد، میتواند از نسبت های مساوی استفاده کند. در واقع، مارال ابتدا باید نسبتی برای تعداد فنجانهای آرد و تعداد فنجانهای کره بنویسد. نسبت تعداد فنجانهای آرد به تعداد فنجانهای کره، ۳ به ۱ است که بهشکل کسر زیر نوشته میشود:
در مرحله بعد، مارال باید یک نسبت معادل را با ضرب صورت و مخرج در 3 پیدا کند، زیرا میخواهد ۳ جعبه کیک بپزد.
مارال از این نسبت های مساوی نتیجه میگیرد که برای تهیه 3 جعبه کلوچه به 9 فنجان آرد و 3 فنجان کره نیاز دارد.
مهرههای شکل زیر را در نظر بگیرید. نسبت کل مهرهها به مهرههای آبی چقدر است؟ میخواهیم یک نسبت مساوی برای آن پیدا کنیم.
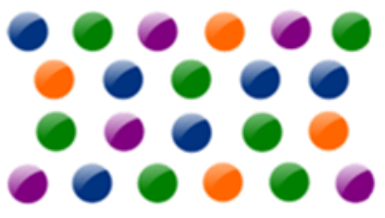
ابتدا تعداد کل مهرهها و همچنین، مهرههای آبی را میشماریم. در مجموع 22 مهره و 6 مهره آبی وجود دارد. سپس، مقادیر را به سه روش مختلف به صورت یک نسبت مینویسیم. تعداد کل مهرهها مقدار اول و تعداد مهرههای آبی مقدار دوم است.
۲۲ به ۶
نسبت کل مهرهها به مهرههای آبی برابر با است. یک نسبت مساوی برای ، کسر است. اما چگونه به این نسبت مساوی رسیدهایم؟ اگر دقت کنید، صورت و مخرج را در ۳ ضرب کردهایم:
دقت کنید که میتوانستیم صورت و مخرج را بر ۲ نیز تقسیم کنیم و یک نسبت مساوی دیگر بنویسیم:
بنابراین، نیز یک نسبت مساوی است.
برای یادگیری بهتر، یک مثال دیگر را بررسی میکنیم. میخواهیم ببینیم نسبت مهرههای نارنجی به مهرههای آبی چقدر است. ابتدا تعداد مهرههای نارنجی و آبی را میشماریم. 4 مهره نارنجی و 6 مهره آبی وجود دارد.
در مرحله بعد، مقادیر را به صورت نسبت کسری مینویسیم. تعداد مهرههای نارنجی کمیت اول و تعداد مهرههای آبی کمیت دوم است.
سپس با ضرب یا تقسیم هر دو کمیت در یک عدد یک نسبت معادل پیدا میکنیم. در این حالت، از شکل کسری نسبت استفاده میکنیم. صورت و مخرج را میتوانیم بر ۲ تقسیم کنیم و یک نسبت معادل بهدست آوریم:
نسبت مهرههای نارنجی به مهرههای آبی است که یکی از معادلهای آن است.
دقت کنید که میتوانستیم به ضرب صورت و مخرج در عددی دلخواه نیز یک نسبت مساوی بهدست آوریم. برای مثال، صورت و مخرج را در ۱۰ ضرب میکنیم:
اکنون میخواهیم ببینیم نسبت مهرههای بنفش به کل مهرهها چقدر است. ابتدا تعداد مهرههای بنفش و تعداد کل مهرهها را میشماریم. 5 مهره بنفش و 22 مهره کلی وجود دارد. در مرحله بعد، مقادیر را به صورت نسبت کسری مینویسیم. تعداد مهرههای بنفش کمیت اول و تعداد کل مهرهها کمیت دوم است.
با ضرب صورت و مخرج در یک عدد، مثلاً ۳، یک نسبت مساوی را مینویسیم:
نسبت های مساوی با شکل
یکی از راههای محاسبات مربوط به نسبت های مساوی، استفاده از شکل است که در این بخش به آن میپردازیم.
فرض کنید به کمک شکل میخواهیم یک نسبت مساوی برای بنویسیم که مخرج آن برابر با ۱۵ باشد. در واقع میخواهیم علامت سؤال را در تساوی زیر مشخص کنیم:
ابتدا باید کسر را با شکل نشان دهیم. بدین منظور، یه مستطیل را به سه قسمت مساوی تقسیم میکنیم، زیرا مخرج ۳ است.

در ادامه، ۲ خانه از ۳ خانه را رنگ میکنیم تا کسر را مشخص کنیم.

چون میخواهیم ببینیم ۲ از ۳ معادل چه عددی از ۱۵ است، شکل را به ۱۵ بخش تقسیم میکنیم.

میبینیم که اصل شکل و قسمت رنگشده ثابت باقی مانده و تنها کاری که کردهایم، افزایش تعداد خانهها بوده است. حال کافی است تعداد خانههای آبی را کوچک را بشماریم. میبینیم که 10 خانه آبی داریم. بنابراین، کسر مساوی است.
دقت کنید که اگر میخواستیم بدون شکل این سؤال را حل کنیم، میتوانستیم بگوییم که در چه عددی ضرب شده که حاصلش است و آن عدد را در صورت نیز ضرب میکردیم. این عدد ۵ است. بنابراین، میتوان نوشت:
همانطور که میبینیم، جواب با آنچه که با کمک شکل بهدست آوردیم برابر است.
کاربرد نسبت های مساوی در زندگی واقعی
همانطور که گفتیم، نسبت های مساوی یک رابطه تنناسبی یکسان بین دو کمیت را نشان میدهند. نسبت به سادگی یک عدد را با عدد دیگر مقایسه میکند و یک نسبت معادل به این معنی است که این رابطه تناسبی ثابت میماند. در واقع، میتوانیم نسبت های مساوی را با ضرب عدد در صورت و مخرج کسر بهدست آوریم. استفاده از نسبتهای مساوی در زندگی واقعی رایج است. برای مثال، وقتی به فروشگاهی میروید و میخواهیم قیمت نهایی چند محصول را که بیش از یک عدد از آن را خریدهاید، محاسبه کنید، از نسبت های مساوی استفاده میکنید. همچنین، مصرف بنزین بهازای پیمایش مقدار مشخصی مسافت، میزان دریافتی در یک شغل با دانستن میزان دریافت ساعتی و... از مثالهای کاربرد این مفهوم هستند.
مثالهای نسبت های مساوی
در این بخش،مثالهایی را از نسبت های مساوی حل میکنیم.
مثال اول نسبت های مساوی
جدول نسبت زیر داده شده است. علامت سؤال باید چه عددی باشد؟
| صورت | مخرج |
| ۱ | ۲ |
| ۲ | ۴ |
| ۳ | ۶ |
| ۴ | ۸ |
| ۵ | ؟ |
| ۱۰ | ؟ |
| ۲۳۳ | ؟ |
حل: نسبت معادل از صورت به مخرج در اینجا ۲ است. به عبارت دیگر، مخرج دور برابر صورت است. بنابراین، میتوانیم هر عدد را در ستون سمت چپ با ضرب عدد سمت راست در ۲ پیدا کنیم.
| صورت | مخرج |
| ۱ | ۲ = ۲ × ۱ |
| ۲ | ۴ = ۲ × ۲ |
| ۳ | ۶ = ۲ × ۳ |
| ۴ | ۸ = ۲ × ۴ |
| ۵ | ۱۰ = ۲ × ۵ |
| ۱۰ | ۲۰ = ۲ × ۱۰ |
| ۲۳۳ | ۴۶۶ = ۲ × ۲۳۳ |
بنابراین، کسرهای زیر معادل هستند:
مثال دوم نسبت های مساوی
آیا نسبتهای و با هم مساوی هستند؟
حل: بله، با ساده کردن کسر ، خواهیم داشت:
$$ \require {cancel} \frac 9 { 60 } = \frac {3 \times 3 } { 3 \times 20} = \frac {\cancel 3 \times 3 }{\cancel 3 \times 20} = \frac {3}{20}$$
همانطور که میبینیم، دو نسبت مساوی هستند.
مثال سوم نسبت های مساوی
یک نسبت معادل برای نسبت ۸ به ۱۸ پیدا کنید.
حل: ابتدا نسبت دادهشده را به صورت کسری بنویسیم.
اکنون صورت و مخرج را در 2 ضرب میکنیم:
بنابراین، یک نسبت معادل ۱۶ به ۳۶ است.
مثال چهارم نسبت های مساوی
یک کیسه حاوی 4 توپ قرمز و 9 توپ سفید است. نسبت توپهای قرمز به توپهای سفید چقدر است؟
حل: تعداد توپهای قرمز برابر با 4 و تعداد توپهای سفید برابر با 9 است. بنابراین، نسبت توپهای قرمز به توپهای سفید است.
مثال پنجم نسبت های مساوی
پنج نسبت مساوی با 4/7 بنویسید.
حل: کافی است صورت و مخرج را در ۵ عدد مختلف ضرب کنیم. برای این کار میتوانیم از جدول زیر استفاده کنیم.
| مخرج | صورت |
| ۷ | ۴ |
| ۱۴ = ۲ × ۷ | ۸ = ۲ × ۴ |
| ۲۱ = ۳ × ۷ | ۱۲ = ۳ × ۴ |
| ۳۵ = ۵ × ۷ | ۲۰ = ۵ × ۴ |
| ۷۰ = ۱۰ × ۷ | ۴۰ = ۱۰ × ۴ |
| ۱۴۰ = ۲۰ × ۷ | ۸۰ = ۲۰ × ۴ |
بنابراین، میتوان گفت نسبتهای زیر مساوی هستند:
مثال ششم نسبت های مساوی
شکل زیر را در نظر بگیرید و پاسخ پرسشهای زیر را بنویسید.

الف) نسبت تعداد مرغها به تعداد جوجهها را بنویسید.
ب) آیا نسبت جوجههای بدون لباس به کل جوجهها با نسبت جوجههای با لباس سفید به کل جوجهها برابر است؟
ج) یک نسبت مساوی برای نسبت تعداد جوجههای با لباس سبز به کل جوجهها بنویسید.
حل الف: نسبت تعداد مرغها به تعداد جوجهها ۱ به ۵ یا است.
حل ب: نسبت جوجههای بدون لباس به کل جوجهها ۲ به ۵ است. همچنین، نسبت جوجههای با لباس سفید به کل جوجهها ۲ به ۵ است. بنابراین، این دو نسبت برابر هستند.
حل ج: نسبت تعداد جوجههای با لباس سبز به کل جوجهها ۱ به ۵ یا است. برای نوشتن نسبت های مساوی، کافی است صورت و مخرج را در یک عدد دلخواه ضرب کنیم. در اینجا عدد ۲ را در صورت و مخرج ضرب میکنیم:
بنابراین، مساوی است.
مثال هفتم نسبت های مساوی
احمد با مخلوط کردن 3 فنجان موز با 2 فنجان آب سیب، یک پارچ سیبموز درست میکند. او اگر بخواهد ۴ پارچ سیبموز درست کند، به چه مقداری از آب سیب و موز نیاز دارد؟
حل: ابتدا نسبت مقدار موز به آب سیب را مینویسیم. این نسبت ۳ به ۲ یا بهشکل کسری است. برای بهدست آوردن مقادیر لازم آب سیب و موز برای ۴ پارچ سیبموز، باید یک نسبت معادل بهدست بیاوریم. برای این کار، صورت و مخرج را در ۴ ضرب میکنیم.
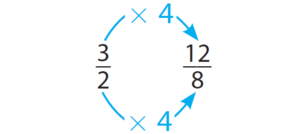
بنابراین، باید ۱۲ فنجان موز با ۸ فنجان آب سیب استفاده کنیم.
مثال هشتم نسبت های مساوی
در شکل زیر، نسبت مساحت مستطیل کوچک را به مساحت مستطیل بزرگ بنویسید و یک نسبت مساوی برای آن ارائه دهید. مساحت هر خانه کوچک را ۱ واحد مربع در نظر بگیرید.
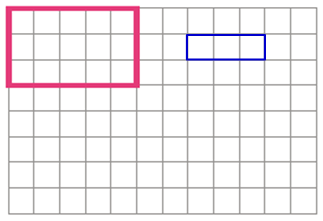
حل: مساحتها برابر با تعداد خانههای درون هر مستطیل است. بنابراین:
- مساحت مستطیل کوچک: ۳
- مساحت مستطیل بزرگ: ۱۵
بنابراین، نسبت مساحت مستطیل کوچک به مساحت مستطیل بزرگ ۳ به ۱۵ یا است. برای نوشتن کسر معادل، میتوانیم صورت و مخرج را بر ۳ تقسیم کنیم:
بنابراین، و نسبت های مساوی هستند.
جمعبندی
در این آموزش با نسبت های مساوی و روشهای بهدست آوردن آنها آشنا شدیم و مثالهای متنوعی از آن را بررسی کردیم.
آزمون نسبت های مساوی
۱. در هنگام بیان نسبت جزء به جزء و جزء به کل، چه نکتهای باید رعایت شود تا معنا تغییر نکند؟
برای نسبت جزء به کل همیشه از کلمه 'کل' استفاده میشود.
میتوان هر عددی را اول یا دوم قرار داد.
باید همیشه جمع کمیتها به عنوان نسبت نوشته شود.
ترتیب کمیتها را با توجه به پرسش مشخص کنیم.
در نوشتن نسبت جزء به جزء یا جزء به کل، بسیار مهم است که ترتیب کمیتها بر اساس آنچه پرسیده شده رعایت شود و کمیت مورد سوال ابتدا یا انتها قرار گیرد، بنابراین پاسخ «ترتیب کمیتها را با توجه به پرسش مشخص کنیم» درست است.
۲. اگر صورت و مخرج یک نسبت را به طور همزمان در یک عدد ضرب یا تقسیم کنیم، نتیجه چه خواهد بود و چرا؟
مخرج دو برابر میشود اما مقدار نسبت نصف میشود.
فقط صورت تغییر میکند و نسبت عوض میشود.
نسبت تغییر نمیکند زیرا مقدار تقسیم ثابت میماند.
نسبت بزرگتر میشود چون هر دو عدد افزایش مییابند.
وقتی صورت و مخرج یک نسبت را به طور همزمان در یک عدد ضرب یا تقسیم کنیم، مقدار تقسیم آنها ثابت میماند و بنابراین نسبت تغییر نمیکند. این ویژگی مانند کسرهای معادل است که اگر صورت و مخرج هر دو با یک عدد ضرب یا تقسیم شوند، همچنان مقدار کلی ثابت میماند.
۳. اگر نسبت مهرههای آبی به کل مهرهها ۲ به ۳ باشد و بخواهیم نسبت مساوی با کل ۹ مهره بنویسیم، چه باید کرد؟
تعداد مهرههای آبی را همزمان در ۳ ضرب کنیم.
هر دو مقدار را به ۹ تقسیم کنیم.
فقط تعداد کل مهرهها را در ۳ ضرب کنیم.
تعداد مهرههای آبی را در ۲ و کل مهرهها را در ۳ ضرب کنیم.
در این حالت چون نسبت ۲ به ۳ است و میخواهیم نسبت جدیدی بنویسیم که مجموع مهرهها ۹ باشد، باید هر دو عدد نسبت اولیه را همزمان در ۳ ضرب کنیم. بنابراین ۲ × ۳ برابر با ۶ مهره آبی و ۳ × ۳ برابر با ۹ مهره کل خواهد شد. این کار نسبت مساوی ایجاد میکند چون همزمان هر دو عدد تغییر کردهاند.
۴. وقتی در یک جدول داده دو نسبت به صورت کسر نوشته شدهاند، طبق روش آموزش داده شده برای تشخیص مساوی بودن این نسبتها کدام راه مناسب است؟
هر دو نسبت را ساده کنیم و اگر مساوی شدند، نتیجه بگیریم که نسبتها مساویاند.
صورت را در مخرج نسبت دیگر ضرب و مقایسه کنیم که حاصل برابر شود.
عددها را با یک روش دلخواه ضرب یا تقسیم کنیم و اگر هر دو کسر تغییر مشابهی داشتند، نسبتها مساویاند.
فقط صورت کسرها را با هم مقایسه کنیم و اگر برابر بودند، نسبت یکسان است.
برای یافتن نسبتهای مساوی باید هر دو کمیت (صورت و مخرج) را همزمان با یک عدد ضرب یا تقسیم کنیم و مقادیر جدید را با نسبت دوم مقایسه کنیم. روش مقایسه فقط صورت یا ساده کردن صرف کافی نیست. استفاده از ضرب یا تقسیم همزمان روی هر دو عدد و تطبیق نسبت جدید با نسبت دیگر، نشاندهنده برابری نسبتهاست.
۵. در حل نسبتهای مساوی با روش تصویری، برای یافتن مقدار مجهول باید چه کاری انجام داد؟
فقط مقدار عددی نسبت اولیه را تقسیم کنیم تا مقدار مجهول پیدا شود.
همه خانهها را به یک رنگ درآوریم تا مقایسه راحتتر شود.
تعداد خانههای رنگی مربوط به نسبت اولیه را در کل جدید شمارش کنیم.
تعداد کل خانههای رنگی را افزایش داده و دوباره نسبت بگیریم.
برای یافتن مقدار مجهول در نسبتهای مساوی با روش تصویری، باید تعداد خانههای رنگی همان نسبت اولیه را در کل جدید خانهها بشماریم. این کار باعث میشود نسبت بین رنگآمیزی و تعداد کل بهصورت مساوی حفظ شود.












