مقایسه اعداد اعشاری – به زبان ساده + مثال
در آموزشهای پیشین مجله فرادرس، با اعداد اعشاری و جمع آنها آشنا شدیم. در این آموزش، روش مقایسه اعداد اعشاری را شرح میدهیم.

مقایسه اعداد اعشاری به معنای یافتن عدد اعشاری بزرگتر و کوچکتر در مجموعهای از اعداد است. اعداد اعشاری را میتوان به همان روشی که ما اعداد دیگر را مقایسه میکنیم، مقایسه کنیم. با این حال، باید به یاد داشته باشیم که ارقامی که بعد از ممیز اعشار قرار میگیرند نیز باید در نظر گرفته شوند. این ارقام دارای مقادیری هستند که از یکدهم شروع میشود، بهدنبال آن صدم میآید، سپس هزارم، و غیره. پیش از بررسی روش مقایسه اعداد اعشاری، ویژگیهای اعداد اعشاری را مرور خواهیم کرد.
مروری بر اعداد اعشاری
اعداد اعشاری دستهای از اعداد هستند که برای نمایش مقدارهایی به کار میروند که با اعداد شمارشی عادی (مانند ۱ و ۲ و ۳ و...) نمیتوان آنها را بیان کرد. اعشار را با ممیز (یعنی تمایزدهنده) نمایش میدهیم. در دستور خط فارسی، علامت ممیز یک خط کوچک کج است. برای مثال، پنج و هفت دهم را به صورت ۵٫۷ مینویسیم. در زبان انگلیسی، ممیز را با نقطه نشان میدهند. مثلاً همان عدد پنج و هفت دهم در زبان انگلیسی به صورت نمایش داده میشود.
نکته: توجه کنید که علامت کسر (/) با ممیز (٫) فرق دارد و اغلب به اشتباه به جای ممیز به کار میرود.
اکنون، نحوه نمایش و جایگاه ارقام در اعداد اعشاری را معرفی میکنیم. عدد ۲۳٫۰ را در نظر بگیرید که میدانیم همان ۲۳ است. این عدد به معنی ۲ دهتایی و ۳ یکی است و چون بخشهای کوچکتری از یک واحد ندارد، بعد از ممیز عددی قرار نمیگیرد. با یک مقایسه کوچک، مشاهده میکنیم که سمت راست ممیز، دهمها، صدمها، هزارمها و… و سمت چپ آن، دهگانها، صدگانها، هزارگانها و… را نمایش میدهند. تصویر زیر این موضوع را بهخوبی نشان میدهد.

در تصویر بالا، در سمت راستِ ممیزِ شکل بالا، هرچه به سمت راست میرویم، ارزش اعداد کم میشود. همچنین در سمت چپ ممیز، هرچه به سمت چپ میرویم، ارزش اعداد افزایش مییابد.
نکته: هنگامی که ممیز در عددی به کار میرود، باید آن را با عدد بدون ممیز تمایز دهیم. برای مثال، عدد ۱٫۰۰۰ همان یک است و ۱۰۰۰ عدد هزار را نمایش میدهد.
مقایسه اعداد اعشاری
مقایسه اعداد اعشاری عملی مشابه مقایسه اعداد صحیح است که در آن ارقام را با بیشترین ارزش مکانی مقایسه میکنیم. اعداد اعشاری داده شده را در جدول ارزش مکانی قرار میدهیم و مقایسه را شروع میکنیم. جدول ارزش مکانی، چیزی مشابه تصویر بالاست. برای مثال، جدول ارزش مکانی عدد بهصورت زیر است.
| صدم | دهم | ممیز | یکان | دهگان |
| ۵ | ۳ | ٫ | ۲ | ۱ |
همانطور که گفتیم، برای مقایسه دو عدد اعشاری، هردو را در جدول ارزش مکانی قرار میدهیم. سپس از رقمی با بالاترین ارزش، یعنی از سمت چپترین رقم شروع میکنیم و مقایسه را انجام میدهیم. اگر ارقام روی بزرگترین ارزش مکانی یکسان باشند، به ارقام مکان بعدی سمت راست میرویم. به همین منوال، به مقایسه ارقام ادامه میدهیم تا زمانی که به ارقام متفاوت برسیم. با کمک مثال زیر این موضوع را شرح میدهیم.
برای مثال، میخواهیم دو عدد و را مقایسه کنیم. ابتدا جدول ارزش مکانی را تشکیل و دو عدد را در آن قرار میدهیم.
| هزارم | صدم | دهم | ممیز | یکان |
| ۲ | ۶ | ۳ | ٫ | ۰ |
| ۰ | ۴ | ۶ | ٫ | ۰ |
- نکته: دقت کنید که در جدول بالا، بهجای عدد را قرار دادهایم، زیرا صفر انتهای عدد پس از اعشار، تغییری در آن ایجاد نمیکند. این کار را به این دلیل انجام دادیم که تعداد ارقام دو عدد با هم برابر شوند.
- نکته: همچنین، صفر قبل از بخش صحیح عدد اعشاری تغییری در مقدار عدد ایجاد نمیکند. برای مثال، میتوانیم بهجای عدد عدد را بنویسیم.
به مثال برمیگردیم. جدول ارزش مکانی دو عدد را در نظر بگیرید. مقایسه را طی مراحل سادهای انجام میدهیم.
- مرحله 1: قسمت اعداد کامل را که رقم یکان است مقایسه میکنیم. اگر اعداد یکسان باشند، به مرحله بعد میرویم. در این حالت، رقم یکان در هر دو عدد است. بنابراین، به مکان بعدی سمت راست میرویم.
- مرحله 2: مکان دهم را که در سمت راست اعشار یا ممیز است، مقایسه میکنیم. وقتی مقدار را در مکان دهم مقایسه کنیم، میبینیم که بزرگتر از است. در این مرحله متوجه میشویم که بزرگتر از است. بنابراین، برای مقایسه بیشتر نیازی به حرکت به سمت رقم صدم نیست.
- مرحله 3: بنابراین، نتیجه میگیریم که .
مقایسه اعداد اعشاری با اعداد کسری
کسرها دستهای از اعداد هستند که با تقسیم دو عدد صحیح تعریف میشوند و برای نشان دادن هر تعداد از قسمتهای مساوی یک چیز بهکار میروند. در واقع، کسرها اعدادی حقیقی بهفرم هستند که در آنها و اعدادی صحیح هستند. عدد صورت کسر و عدد مخرج کسر نامیده میشود. بنابراین، در کسر عدد ۲ صورت و عدد ۳ مخرج کسر است و آن را «دو سوم» میخوانیم.
گاهی پیش میآید که میخواهیم اعداد اعشاری را با اعداد کسری مقایسه کنیم. در این مواقع که به مقایسه اعشار و کسر نیاز داریم، ابتدا کسر داده شده را به یک عدد اعشاری تبدیل میکنیم و سپس اعداد را با همان روش مقایسه اعداد اعشاری با هم مقایسه میکنیم.
برای مثال، میخواهیم دو کسر و را مقایسه کنیم. برای انجام این مقایسه، ابتدا اجازه دهید را، با تقسیم بر ، به یک عدد اعشاری تبدیل میکنیم. با توجه به آنچه که در آموزش «تبدیل کسر به اعشار — به زبان ساده + حل تمرین و مثال» از مجله فرادرس یاد گرفتیم، این کار را انجام میدهیم.
همانطور که مشخص است، مخرج کسر مضرب ، یعنی ، ، و... نیست. بنابراین، باید آن را به مضربی مناسب از تبدیل کنیم تا بهراحتی آن را بهشکل یک عدد اعشاری بنویسیم. با ضرب مخرج در عدد ، میتوانیم آن را به تبدیل کنیم. دقت کنید که هنگام ضرب یک عدد در مخرج، حتماً باید آن را در صورت نیز ضرب کنیم تا اثر ضرب مخرج خنثی شود. بنابراین، داریم:

بنابراین، کسر معادل با کسر است. اکنون مخرج این کسر مضربی از است و میتوانیم آن را به اعشار تبدیل کنیم. بدین منظور، عدد را مینویسیم و از سمت راست، دو رقم (تعداد صفرهای ) را از آن جدا میکنیم. در نهایت، عدد اعشاری معادل کسر ، برابر خواهد بود با
اکنون هر دو عدد را بهشکل اعشاری داریم. بنابراین، دو عدد و را با استفاده از روش ذکرشده در بالا مقایسه کنیم. ابتدا اجدول ارزش مکانی دو عدد را تشکیل میدهیم.
| هزارم | صدم | دهم | ممیز | یکان |
| ۰ | ۵ | ۷ | ٫ | ۰ |
| ۸ | ۲ | ۷ | ٫ | ۰ |
- مرحله 1: ابتدا قسمت صحیح اعداد را که رقم یکان است مقایسه میکنیم. در این حالت، رقم یکان در هر دو عدد است و نمیتوان نتیجه خاصی گرفت. بنابراین، به ارزش مکانی بعدی به سمت راست خواهیم رفت.
- مرحله 2: مکان دهم را که اولین مکان سمت راست ممیز است، مقایسه میکنیم. وقتی مقدار رقم دهم را مقایسه میکنیم، میبینیم که هر دو رقم هستند. بنابراین، یک رقم دیگر به راست میرویم و ارقام مکان صدم را مقایسه میکنیم.
- مرحله 3: مکانهای صدم را مقایسه میکنیم. اکنون وقتی مقدار را در مکان صدم مقایسه میکنیم، می بینیم که بزرگتر از است. در این مرحله، متوجه میشویم که بزرگتر از است. بنابراین، برای مقایسه بیشتر نیازی به حرکت به سمت رقم هزارم نیست.
- مرحله ۴: بنابراین، نتیجه میگیریم که و این یعنی .
مقایسه اعداد اعشاری با اعداد مخلوط
مقایسه اعداد اعشاری با اعداد مخلوط، شبیه مقایسه اعداد اعشاری با اعداد کسری است. میتوانیم عدد مخلوط را به کسر و سپس به عدد اعشاری تبدیل کنیم، سپس مقایسه را انجام دهیم. کار دیگری که میتوانیم انجام دهیم، این است که بخش کسری عدد مخلوط را به عدد اعشاری تبدیل کنیم و آن را در کنار عدد کامل عدد مخلوط بنویسیم. سپس مقایسه را انجام دهیم.

برای مثال، فرض کنید میخواهیم عدد اعشاری را با عدد مخلوط مقایسه کنیم. ابتدا، عدد مخلوط را به یک عدد اعشاری تبدیل میکنیم. بدین منظور، در آغاز، عدد مخلوط را به یک کسر متعارفی تبدیل میکنیم:
مخرج این کسر است و باید آن را به یک عدد مضرب تبدیل کنیم. با ضرب آن در به میرسیم که مضرب است. بنابراین، خواهیم داشت:
اکنون، صورت کسر را مینویسیم، و از راست سه رقم اعشار را جدا میکنیم:
بنابراین:
اکنون، دو عدد اعشاری و را داریم که باید آنها را مقایسه کنیم. طبق آنچه گفتیم، کافی است جدول ارزش مکانی ارقام را تشکیل دهیم.
| هزارم | صدم | دهم | ممیز | یکان |
| ۵ | ۲ | ۱ | ٫ | ۲ |
| ۰ | ۵ | ۲ | ٫ | ۲ |
مطابق معمول، از سمت چپ شروع میکنیم. یکان دو عدد برابر هستند. پس، یک رقم به سمت راست میآییم. میبینیم که در رقمهای دهم، از کوچکتر است. بنابراین، مقایسه در اینجا پایان مییابید و مشاهده میکنیم که کوچکتر از است. بنابراین، میتوان نتیجه گرفت که از عدد مخلوط بزرگتر است.
مقایسه اعداد اعشاری روی محور
برای مقایسه اعداد اعشاری روی محور اعداد، باید از قانون اصلی محور اعداد پیروی میکنیم که میگوید هرچه به سمت راست حرکت کنیم ارزش اعداد افزایش مییابد. به عنوان مثال، فرض کنید میخواهیم دو عدد و را با هم مقایسه کنیم. بدین منظور، اعداد اعشاری را روی محور اعداد به گونهای مشخص میکنیم که هر دو عدد کاملاً در معرض دید باشند.
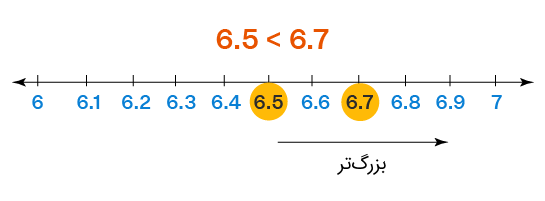
باید بین و تمرکز کنیم، زیرا هر دو عدد داده شده بین و قرار دارند. بدین منظور، عدد را در انتهای سمت چپ و را در انتهای راست محور اعداد علامتگذاری میکنیم. سپس، تمام اعداد بین این دو عدد را با مقیاس دهم علامتگذاری میکنیم. یکدهم یکدهم میشماریم و دو عدد و را مشخص میکنیم. میبینیم که عدد در سمت راست و در سمت چپ قرار میگیرد. بنابراین، عدد اعشاری بزرگتر از است.
مقایسه اعداد اعشاری با اعداد صحیح
مقایسه اعداد اعشاری با اعداد صحیح کار سادهای است. کافی است باز هم جدول ارزش مکانی را تشکیل دهیم. برای مثال، فرض کنید میخواهیم دو عدد و را با هم مقایسه کنیم. کافی است جدول زیر را تشکیل دهیم.
| دهم | ممیز | یکان |
| ۰ | ٫ | ۲ |
| ۵ | ٫ | ۱ |
کافی است از سمت چپ شروع کنیم. دو رقم یکان را مقایسه میکنیم. میبینیم که بزرگتر از است. در اینجا نتیجه میگیریم که بزرگتر از است.
مقایسه اعداد اعشاری منفی
وقتی دو عدد منفی را با هم مقایسه میکنیم، باید به این نکته توجه کنیم که اگر قدر مطلق یک عدد منفی بزرگتر از قدر مطلق عدد دیگر باشد، آن عدد کوچکتر است. برای مثال، عدد صحیح از عدد صحیح بزرگتر است.
برای اعداد اعشاری نیز میتوانیم قدر مطلق آنها را با هم مقایسه کنیم، سپس از قانونی که گفتیم استفاده کنیم. برای مثال، فرض کنید دو عدد و را داریم. برای مقایسه این دو عدد، میتوانیم ابتدا قدر مطلق آنها را با هم مقایسه کنیم. بدین منظور، جدول مقایسه ارزش مکانی را تشکیل میدهیم.
| صدم | دهم | ممیز | یکان |
| ۵ | ۷ | ٫ | ۲ |
| ۰ | ۵ | ٫ | ۲ |
میبینیم که ارقام یکانها با هم برابر است. بنابراین، یک رقم به راست میآییم و دو رقم دهم را مقایسه میکنیم. مشاهده میکنیم که بزرگتر از است. بنابراین، عدد اعشاری بزرگتر از است. اما برای منفی آنها برعکس است. یعنی کوچکتر از است.
نکته: اگر یک عدد منفی را با یک عدد مثبت مقایسه کنیم، نیازی به تشکیل جدول ارزش مکانی ارقام نیست، عدد مثبت همواره از عدد منفی بزرگتر است. برای مثال، عدد همواره از عدد بزرگتر است.
مثالهای مقایسه اعداد اعشاری
در این بخش، مثالهایی از مقایسه اعداد اعشاری را بررسی میکنیم.
مثال اول مقایسه اعداد اعشاری
دو عدد اعشاری و را با هم مقایسه کنید.
جواب: کافی است ارزش مکانی ارقام دو عدد را مقایسه کنیم. اعداد را اینگونه مینویسیم:
| صدگان | دهگان | ممیز | يکان |
| ۷ | ۲ | ٫ | ۰ |
| ۲ | ۳ | ٫ | ۰ |
از سمت چپ شروع میکنیم. میبینیم که یکانها برابر هستند. بنابراین، یک رقم به سمت راست میآییم و دهگانها را مقایسه میکنیم. میبینیم که کوچکتر از است. بنابراین، مقایسه اینجا پایان مییابد و به این نتیجه میرسیم که کوچکتر از است.

مثال دوم مقایسه اعداد اعشاری
دو عدد و را با هم مقایسه کنید.
جواب: نخست، باید عدد را به یک عدد اعشاری تبدیل کنیم. بدین منظور، ابتدا باید مخرج را به عددی تبدیل کنیم که مضرب است. اگر را در ضرب کنیم، چنین چیزی محقق میشود. پس کسر را بهصورت زیر مینویسیم:
اکنون، بهاندازه تعداد صفرهای ، یعنی یک رقم، از سمت راست جدا میکنیم و کسر بهصورت زیر درمیآید:
اگر دقت کنید، را به قسمت تقسیم کنیم، حاصلش میشود .
اکنون باید دو عدد و را مقایسه کنیم. با نگاهی به اعداد درمییابیم که بزرگتر از است. اما این مقایسه را از جدول زیر نیز میتوان نتیجه گرفت که در آن، رقم دهگان بزرگتر از رقم دهگان است.
| دهم | ممیز | یکان | دهگان |
| ۰ | ٫ | ۲ | ۱ |
| ۵ | ٫ | ۴ | ۰ |
مثال سوم مقایسه اعداد اعشاری
دو عدد و را مقایسه کنید.
جواب: ابتدا کسر را به اعشار تبدیل میکنیم.
باید ببینیم عدد را در چه عددی ضرب کنیم تا حاصل مضربی از شود. اگر از ماشین حساب کمک بگیریم، با کمی سعی و خطا به عدد میرسیم و خواهیم داشت:
اکنون، عدد صورت، یعنی را مینویسیم، و از راست چهار رقم اعشار را جدا میکنیم:
اکنون باید دو عدد اعشاری و را مقایسه کنیم. میبینیم که عدد صحیح یکی از آنها است و به همین دلیل بزرگتر است.
مثال چهارم مقایسه اعداد اعشاری
دو عدد اعشاری و را مقایسه کنید و عدد بزرگتر را بیابید.
جواب: همان مراحلی که در بالا بیان کردیم، طی میکنیم.
| هزارم | صدم | دهم | ممیز | یکان |
| ۱ | ۹ | ۳ | ٫ | ۸ |
| ۲ | ۶ | ۳ | ٫ | ۸ |
- مرحله 1: ابتدا اعداد صحیح کامل را با هم مقایسه میکنیم. در این مثال، قسمت اعداد کامل در هر دو عدد است. بنابراین، ما به ارزش مکانی بعدی میرویم.
- مرحله 2: مکان دهم را که اولین مکان سمت راست نقطه اعشار است، مقایسه میکنیم. وقتی مقدار رقم دهم را مقایسه میکنیم، میبینیم که هر دو عدد رقم 3 را دارند. از این مرحله نیز عبور میکنیم و به مکان صدم میرویم.
- مرحله 3: ارقام مکان صدم را مقایسه میکنیم. اکنون، وقتی مقدار را در مکان صدم مقایسه میکنیم، میبینیم که بزرگتر از است. بنابراین، به این نتیجه میرسیم که بزرگتر از است. در نتیجه، برای مقایسه بیشتر نیازی به حرکت به سمت رقم هزارم نیست.
- مرحله ۴: بنابراین، نتیجه میگیریم که .
مثال پنجم مقایسه اعداد اعشاری
دو عدد و را مقایسه کنید.
جواب: ابتدا جدول ارزش ارقام دو عدد را تشکیل میدهیم.
| صدم | دهم | ممیز | یکان |
| ۴ | ۰ | ٫ | ۲ |
| ۰ | ۴ | ٫ | ۲ |
از سمت چپ شروع و ارقام یکانهای دو عدد را با هم مقایسه میکنیم. این دو رقم برابر هستند. بنابراین، یک رقم به سمت راست میرویم و دهمها را مقایسه میکنیم. میبینیم که رقم دهم بزرگتر از است. اکنون مقایسه پایان مییابد و نتیجه میگیریم که عدد بزرگتر از است.

مثال ششم مقایسه اعداد اعشاری
بهجای مربع بین اعداد زیر، یکی از علامتهای یا یا را قرار دهید.
الف)
ب)
ج)
د)
جواب: علامت درست بین اعداد در ادامه مشخص شده است. سعی کنید خودتان مراحل مقایسه را برای بررسی صحت جوابها طی کنید.
الف)
ب)
ج)
د)
جمعبندی
در این آموزش از مجله فرادرس، ابتدا اعداد اعشاری را مرور کردیم. دیدیم که اعداد اعشاری را با طی مراحل ساده و با تشکیل جدول ارزش مکانی ارقام میتوان با هم مقایسه کرد. همچنین، مقایسه اعداد اعشاری با اعداد صحیح، اعداد مخلوط و اعداد کسری را بیان کردیم. در پایان نیز به بررسی چند مثال پرداختیم.
آزمون اعداد اعشاری
۱. در نظام عددنویسی اعشاری، ممیز اعشاری در فارسی و انگلیسی به چه صورتی نمایش داده میشود و چه تفاوتی با علامت کسر دارد؟
در فارسی و انگلیسی ممیز خط مورب بلند است و علامت کسر با ممیز تفاوتی ندارد.
در هر دو زبان ممیز نقطه است و علامت کسر همان ممیز است.
در فارسی ممیز یک خط افقی و در انگلیسی ویرگول و علامت کسر نقطه است.
در فارسی ممیز خط مورب کوتاه و در انگلیسی نقطه است و علامت کسر متفاوت از هر دو است.
در نظام اعشاری، ممیز اعشاری در فارسی به صورت خط مورب کوتاه نوشته میشود، اما در انگلیسی نقطه به عنوان ممیز اعشاری استفاده میگردد. علامت کسر با هر دو متفاوت است و نباید با ممیز اشتباه گرفته شود.
۲. چرا هنگام مقایسه اعداد اعشاری باید به ارزش رقمهای بعد از ممیز توجه ویژه داشت؟
زیرا ممیز فقط جداکننده اعداد صحیح و اعشاری است.
زیرا همه اعداد اعشاری ارزش یکسانی دارند و نیازی به توجه نیست.
زیرا فقط رقم اول بعد از ممیز اهمیت دارد و بقیه بیاثراند.
زیرا هر رقم بعد از ممیز نمایانگر مقدارهایی مانند دهم یا صدم است.
دلیل اهمیت رقمهای بعد از ممیز این است که هر یک از آنها بیانگر مقدارهای متفاوتی مانند دهم، صدم یا هزارم بوده و ارزش عدد را تعیین میکند.
۳. برای مقایسه اعداد اعشاری با کمک جدول ارزش مکانی، کدام روند باعث میشود نتیجه مقایسه دقیقتر به دست آید؟
صرفا بخش صحیح اعداد اعشاری را مقایسه کنیم و بخش اعشاری را نادیده بگیریم.
عددها را کنار هم نوشته و تا پیدا شدن تفاوت ارقام از چپ، رقم به رقم مقایسه کنیم.
فقط بزرگترین رقم بعد از ممیز را در جدول مقایسه کنیم و سایر ارقام را بررسی نکنیم.
همه ارقام بعد از ممیز را به جدول اضافه کنیم و فقط رقم اول را بررسی کنیم.
برای دقت بیشتر در مقایسه اعداد اعشاری با جدول ارزش مکانی، باید عددها را کامل و رقم به رقم از سمت چپ یعنی از بیشترین ارزش مقایسه کنیم و تا هر جا که تفاوتی پیدا نشد به رقمهای بعدی برویم. این روش مانند مقایسه عددهای صحیح است و باعث میشود هیچ تفاوتی از قلم نیفتد. توجه به فقط رقم اول یا بخش صحیح یا فقط بزرگترین رقم اعشاری، امکان دارد باعث نتیجهگیری نادرست در برخی حالتها شود.
۴. برای مقایسه عدد اعشاری با یک عدد کسری، چه زمانی و چگونه باید عدد کسری را به اعشاری تبدیل کنیم؟
فقط زمانی که مخرج کسر عدد صحیح باشد، تبدیل به اعشاری ضروری است.
در همه حالات لازم است عدد کسری را به اعشاری تبدیل کنیم تا بتوانیم مقایسه انجام دهیم.
تبدیل کسری به اعشاری فقط زمانی انجام میشود که هر دو عدد بزرگتر از یک باشند.
وقتی بخواهیم به روش جدول ارزش مکانی مقایسه کنیم، عدد کسری را با تقسیم صورت بر مخرج به عدد اعشاری تبدیل میکنیم.
اگر بخواهیم برای مقایسه عدد اعشاری و عدد کسری از جدول ارزش مکانی کمک بگیریم، باید ابتدا کسر را به عدد اعشاری تبدیل کنیم تا فرمت اعداد یکسان باشد. این تبدیل با تقسیم صورت به مخرج انجام میشود.
۵. برای مقایسه عدد با ، بهترین روش کدام است و چرا باید آن را انتخاب کنیم؟
فقط بخش صحیح هر عدد را با هم مقایسه کنیم.
اعداد را بدون تبدیل و فقط به صورت ظاهری مقایسه کنیم.
هر دو عدد را به عدد اعشاری تبدیل کرده و سپس به کمک جدول ارزش مکانی مقایسه کنیم.
هر دو عدد را به عدد صحیح تبدیل کرده و سپس مقایسه کنیم.
روش صحیح، تبدیل هر دو عدد به عدد اعشاری و سپس مقایسه رقم به رقم با جدول ارزش مکانی است. این کار باعث میشود ارزش هر رقم را دقیق بسنجیم و نتیجه درست بگیریم. تبدیل به عدد صحیح یا فقط مقایسه بخش صحیح باعث اشتباه میشود و مقایسه ظاهری بدون تبدیل ممکن است نتیجه غلط بدهد.
۶. در مقایسه دو عدد اعشاری منفی مانند -۲٫۵ و -۲٫۷۵، با توجه به جدول ارزش مکانی و قاعده قدر مطلق، کدام انتخاب درست است؟
عدد -۲٫۷۵ بزرگتر از -۲٫۵ است، چون رقمها پس از ممیز بیشتراند.
عدد -۲٫۵ و -۲٫۷۵ برابراند، چون پیش از ممیز یکساناند.
عدد -۲٫۵ بزرگتر از -۲٫۷۵ است، چون هر عدد منفی با قدر مطلق کمتر بزرگتر است.
همیشه عدد با ممیز کوتاهتر مقدار بیشتری دارد.
در مقایسه اعداد اعشاری منفی، باید ابتدا قدر مطلق آنها را بررسی کنیم و سپس با جدول ارزش مکانی مقایسه را انجام دهیم. هرچه قدر مطلق یک عدد منفی بزرگتر باشد، خود عدد کوچکتر است.
۷. در مقایسه سه عدد اعشاری که تعداد رقمهای بعد از ممیز آنها برابر نیست، افزودن صفر به انتهای ارقام اعشار چه کمکی به نتیجهگیری دقیقتر میکند؟
طول اعشار را همسان کرده و مقایسه را آسانتر میکند.
باعث میشود ارزش ارقام قبل از ممیز تغییر کند.
فقط در محاسبه مقدار کسری کاربرد دارد.
جمع اعداد اعشاری را سادهتر میکند.
افزودن صفر به انتهای ارقام اعشار، مانند نوشتن ۰٫۶۰ به جای ۰٫۶ یا ۰٫۷۰۰ به جای ۰٫۷، باعث میشود تعداد رقمهای اعشار همه اعداد برابر شود. این روش بر ارزش عدد اثری ندارد، اما مقایسه ارقام را از لحاظ موقعیت دقیقتر و شفافتر میکند.













سلام خسته نباشید واقعا با آموزش جامع وکاملتون منو از سر در گمی نجات دادید بسیار تشکر میکنم از زحماتی که کشیدید آرزوی سلامتی برای دست اندر کاران این آموزشگاه را دارم موفق وپیروز باشید❤