معادله چیست؟ — به زبان ساده

در این آموزش از مجموعه مطالب ریاضی مجله فرادرس، به این پرسش پاسخ می‌دهیم که معادله چیست و چگونه باید آن را حل کنیم.

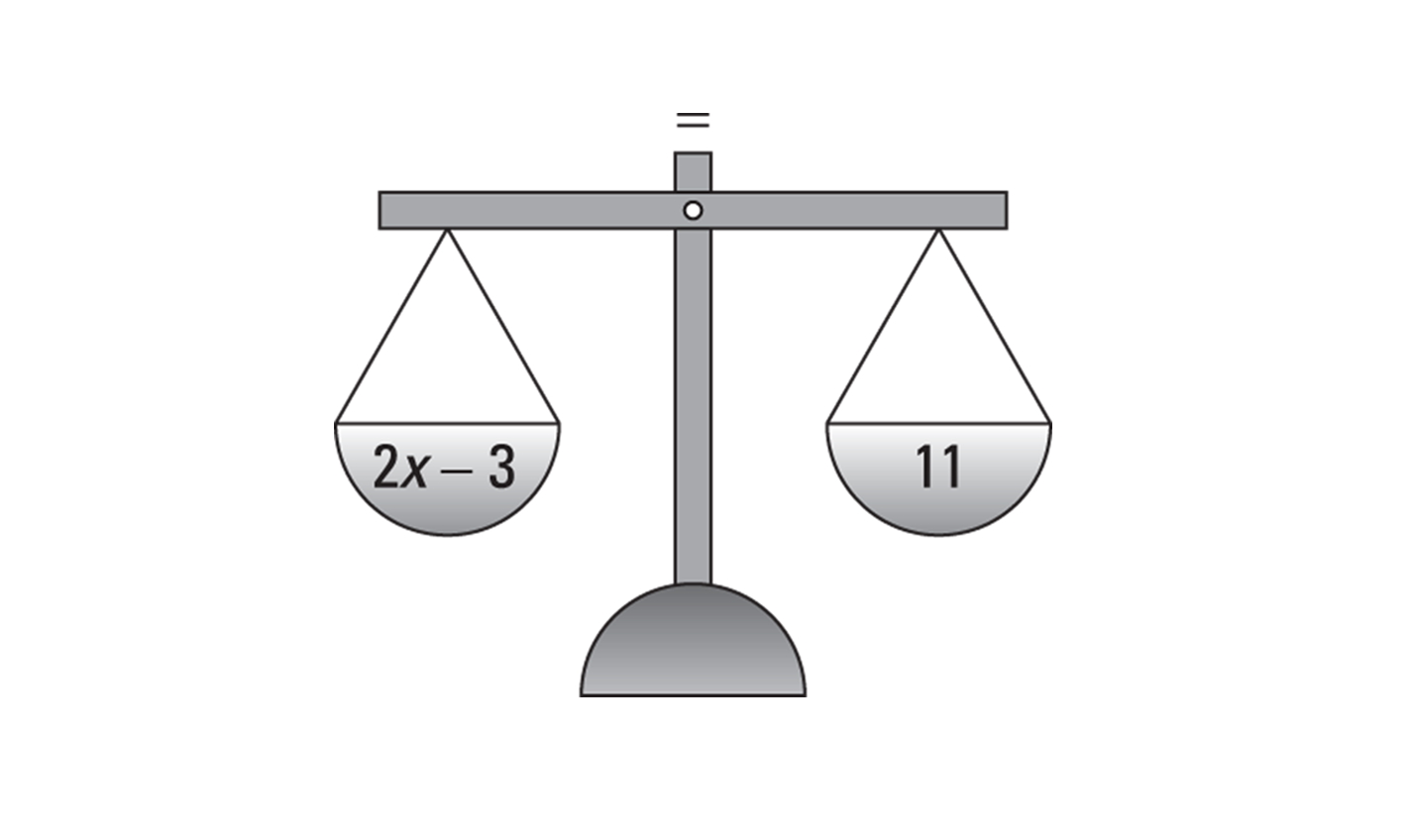
معادله چیست ؟

«معادله» (Equation) واژه‌ای عربی و در لغت به‌معنی برابری و هم‌وزنی است. همین معنی به ما می‌گوید که به زبان ریاضی باید یک مساوی داشته باشیم. به‌عبارت بهتر، معادله یک گزاره ریاضی است که تساوی دو عبارت را بیان می‌کند و این تساوی با علامت "=" نمایش داده می‌شود.

فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم در فرادرس

کلیک کنید

برای مثال، عبارت $$5 + 3$$ برابر با عبارت $$6 + 2$$ است، زیرا مجموع هر دو برابر با $$8$$ است. بنابراین، می‌توانیم معادله زیر را بنویسیم:

$$\large 5 + 3 = 6 + 2$$

تساوی‌های زیر دو معادله را نشان می‌دهند:

$$\large \begin {align*} 6-2& =3 + 1 \\ 7-4& =3 \end {align*}$$

پس اکنون تفاوت معادله و عبارت را می‌دانیم.

حل معادله یا جواب معادله چیست ؟

حل یا جواب معادله چیست ؟ حل یک معادله دارای متغیر، شامل تعیین این است که کدام مقادیر از متغیرها برابری را درست می‌کنند. متغیرهایی که معادله باید برای آن‌ها حل شود «مجهول» نامیده می شوند و مقادیر مجهولاتی که برابری را برقرار می‌کنند «حل» یا «جواب» معادله نامیده می‌شوند.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

آنچه در ابتدای آموزش دیدیم، معادله‌هایی بودند که دو سمت آن‌ها عدد بود، اما اغلب معادله‌ها در ریاضیات شامل حداقل یک متغیر هستند. ابتدایی‌ترین و رایج‌ترین معادلات جبری در ریاضیات نیز از یک یا چند متغیر تشکیل شده‌اند. به‌عنوان مثال، $$x + 2 = 6$$ معادله‌ای است که در آن، $$x + 2$$ و $$6$$ دو عبارتی هستند که با علامت «مساوی» یا "=" با هم مربوط شده‌اند. در یک معادله جبری، مانند هر معادله دیگری، سمت چپ با سمت راست برابر است.

در اینجا، برای مثال، $$5x + 9$$ عبارت سمت چپ است که برابر است با عبارت $$24$$ در سمت راست.

تصویر زیر یک معادله را نشان می‌دهد که اجزای آن مشخص شده‌اند.

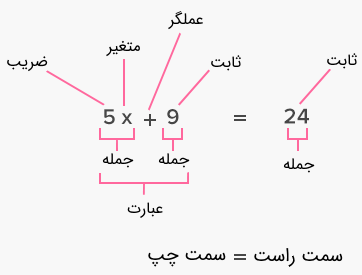
اما حل معادله چیست ؟ معادله $$x +2 = 3$$ را در نظر بگیرید که در آن، $$x = 4$$ یک معادله صحیح را می‌سازد و $$x = 3$$ یک معادله غلط.

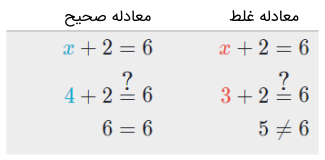
توجه کنید که از علامت $$\stackrel{\large?}{=}$$ در مواقعی استفاده می‌کنیم که مطمئن نیستیم یک معادله صحیح یا غلط داریم. همان‌طور که پیش‌تر گفتیم، مقداری از متغیر که به‌ازای آن یک معادله صحیح خواهد بود، یک جواب یا حل معادله نامیده می‌شو. برای مثال قبلی که بیان کردیم، $$x = 4$$ جواب معادله $$x + 2 = 6$$ است زیرا یک معادله صحیح را می‌سازد.

یک مثال را بررسی می‌کنیم. می‌خواهیم بدانیم از بین دو عدد $$6$$ و $$7$$، کدام‌یک جواب معادله $$3 + g = 10$$ است. برای رسیدن به پاسخ، هر دو مقدار را در معادله قرار می‌دهیم.

از $$g = 6$$ شروع می‌کنیم و می‌بینیم که این عدد جواب معادله نیست:

$$\large \begin {aligned} 3 + g & = 10 \\ 3 + { 6 } & { \large ? }{ = } 10 \\ 9 & \neq 10 \end {aligned}$$

اکنون $$g=7$$ را آزمایش می‌کنیم. با جایگذاری این عدد، می‌بینیم که معادله صحیح بوده و $$g = 7$$ جواب معادله است:

$$\large \begin {aligned} 3 + g & = 10 \\ 3 + {7} & \stackrel { \large ? }{ = } 10 \\ 10 & = 10 \end {aligned}$$

روش حل معادله چیست ؟

در قسمت قبل، چند عدد را داشتیم و در معادله جایگذاری می‌کردیم. پس از آن می‌دیدیم که کدام جواب صحیح است. اما اگر دقت کنید، این روش بسیار وقت‌گیر است و اگر هم وقتش را داشته باشیم، برای معادله‌های پیچیده و حتی ساده کاربردی ندارد و عملاً بسیار دشوار است. بنابراین، باید برای حل معادلات یک روش نظام‌مند داشته باشیم.

در مواردی که با معادلات‌ درجه اول (یعنی $$x$$ با توان 1) سر و کار داریم، بهترین کار برای به‌دست آوردن جواب معادله این است که با اضافه و کم کردن اعداد، $$x$$ را تنها در یک سمت معادله قرار دیم، سپس اگر $$x$$ ضریب داشت، آن را با تقسیم حذف کنیم.

این مراحل را با یک مثال ساده توضیح می‌دهیم. فرض کنید معادله زیر را داریم و می‌‌خواهیم جواب آن را به‌دست آوریم (دقت کنید که در اینجا به‌جای $$x$$ از حرف $$y$$ استفاده شده و هر حرف دیگری نیز می‌تواند متغیر معادله را مشخص کند):

$$3 y-4=17$$

ابتدا عدد $$4$$ را به دو طرف تساوی اضافه می‌کنیم تا عدد $$4$$ سمت چپ حذف شود. دقت کنید که اگر عددی را بخواهیم اضافه کنیم، باید برای هر دو طرف باشد، زیرا یک معادله داریم و دو طرف آن برابر هستند و هر تغییری را که از بیرون بر سمت چپ یا راست اعمال کنیم، باید در دو طرف انجام شود.

به مسئله برمی‌گردیم. گفتیم که عدد $$4$$ را به دو طرف اضافه می‌کنیم. در نتیجه، خواهیم داشت:

$$\begin{aligned} 3 y-4+4 &=17+4 \\ 3 y-1 &=21 \end{aligned}$$

بنابراین، به تساوی زیر می‌رسیم:

$$\large 3 y = 21$$

اکنون باید ضریب $$y$$ را به 1 تبدیل کنیم. برای این کار، دو طرف معادله را بر $$3$$ تقسیم می‌کنیم:

$$\large \frac {3 y } { 3 } = \frac { 21 } { 3 }$$

که در نهایت جواب زیر را به‌دست خواهد داد:

$$\large y = 7$$

در نتیجه، جواب معادله برابر با $$y = 7$$ است. برای راستی‌آزمایی می‌توانید عدد $$7$$ را درون معادله قرار دهید.

چند مثال از حل معادله

در این بخش، حل چند معادله ساده را بررسی می‌کنیم.

فیلم آموزش ریاضی و آمار 1 – پایه دهم علوم انسانی در فرادرس

کلیک کنید

مثال اول حل معادله

معادله $$3 x-2=7$$ را حل کنید.

حل: برای حل این معادله، ابتدا باید از عمل معکوس تفریق، یعنی جمع، استفاده کنیم. بدین ترتیب که عدد $$2$$ را به دو طرف معادله اضافه می‌کنیم و خواهیم داشت:

$$\large 3 x - 2 + 2 = 7 + 2$$

با ساده‌سازی دو طرف معادله، می‌توان چنین نوشت: