معادله هذلولی – به زبان ساده
در مطالب گذشته وبلاگ فرادرس در مورد رویههای فضایی و تعدادی از اشکال هندسی همچون بیضی صحبت کردیم. در این مطلب نیز قصد داریم تا به زبانی ساده، معادله هذلولی و معادلات انواع مختلف آن را مورد بررسی قرار دهیم.

هذلولی چیست؟
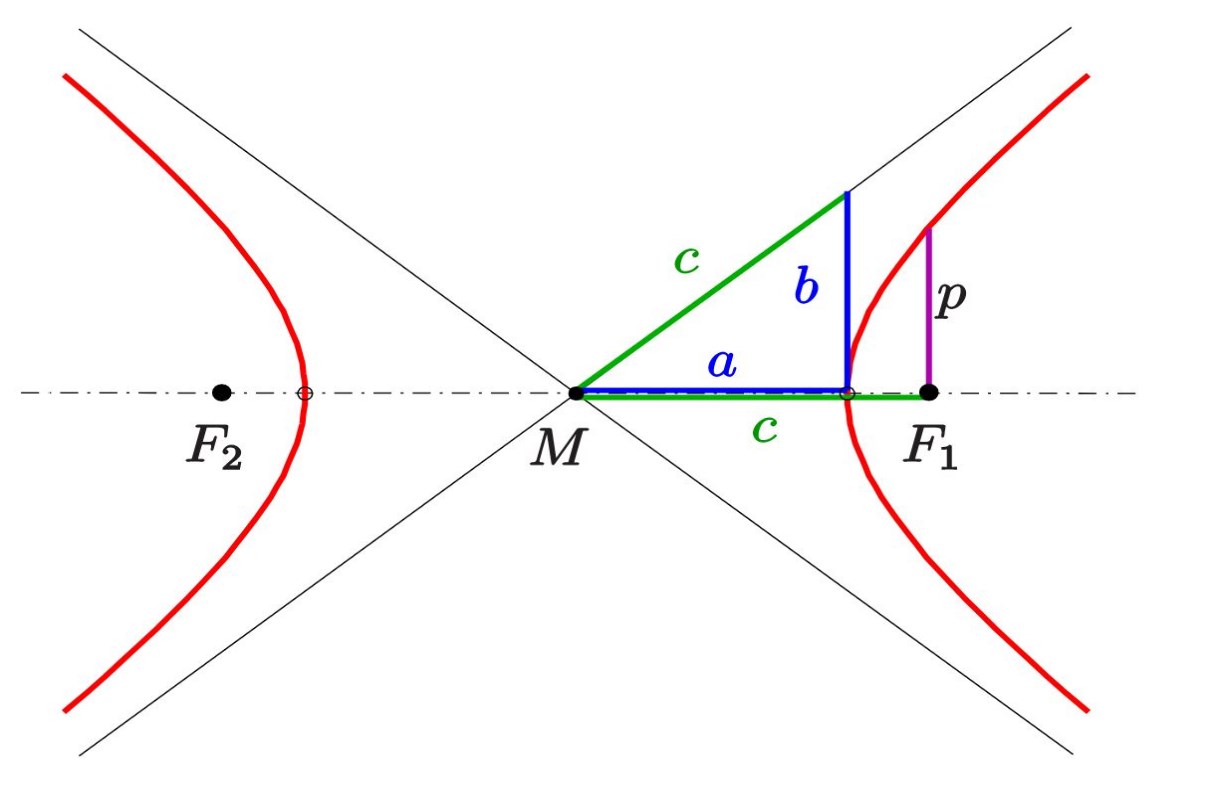
در هندسه تحلیلی، هذلولی منحنی است که با برخورد دادن یک مخروط دوگانه با یک صفحه در زاویهای مشخص بوجود میآید. این تقاطع دو منحنی، دو منحنی جدا از هم ایجاد میکند که دقیقا قرینه یکدیگر هستند.
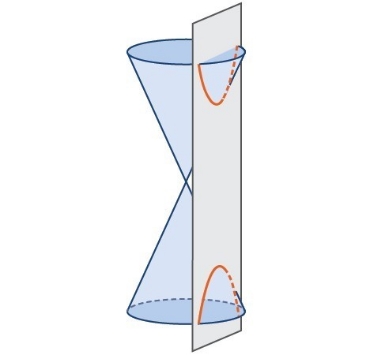
در شکل زیر مخروط، صفحه قطعکننده آن و منحنیهای ایجاد شده، نشان داده شدهاند.
مانند بیضی، هذلولی را نیز میتوان بهعنوان مجموعهای از نقاط قرار گرفته در صفحه مختصات تعریف کرد. به طور دقیقتر میتوان گفت که هذلولی مجموعهای از تمام نقاط صفحه است، به طوری که اختلاف فاصله نقاط از دو نقطه تحت عنوان کانون، مقداری ثابت است. این تعریف بسیار مشابه با تعریف بیضی است. تنها تفاوت در این است که در بیضی، مجموع فواصل از دو کانون عددی ثابت است.
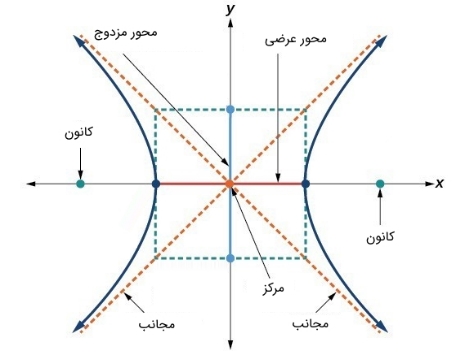
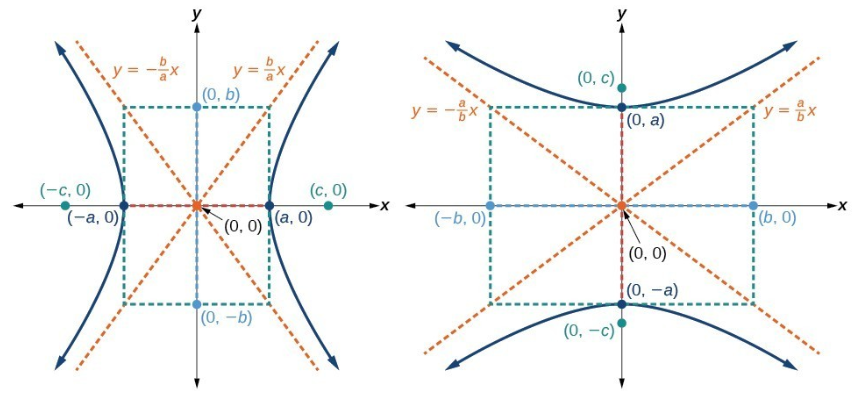
ویژگی مشابه دیگر هذلولی با بیضی این است که هر هذلولی دارای دو محور تقارن است. محور عرضی، خطی است که از مرکز هذلولی عبور میکند و دارای نقاط انتهایی است. کانونها نیز روی محور عرضی قرار میگیرند. محور مزدوج نیز عمود به محور عرضی است و دارای نقاط انتهایی است. مرکز یک هذلولی نیز نقطهای است که دو محور عرضی و مزدوج یکدیگر را قطع میکنند. هر هذلولی نیز دارای دو محور نامتقارن است که هر دوی آنها از مرکز عبور میکنند. در شکل زیر یک هذلولی به همراه اجزای آن نشان داده شدهاند.
در ادامه مطلب، هذلولیهایی را معرفی میکنیم که راستای آنها به صورت افقی یا عمودی است. در این صورت محورها یا منطبق بر محورهای مختصات بوده و یا موازی با دستگاه مختصات خواهند بود.
معادله هذلولی
فرض کنید و دو کانون هذلولی باشند که مرکز آنها در مبدا دستگاه مختصات قرار دارد. از طرفی اختلاف فاصله این کانونها از نقاط روی هذلولی عددی ثابت است.
در شکل زیر چنین هذلولی نشان داده شده است.
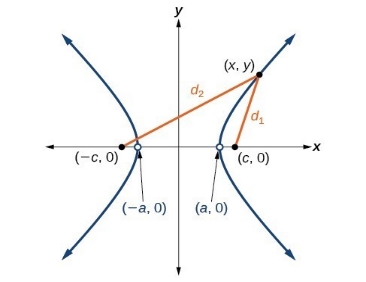
همانطور که میبینید فاصله کانونها با نقاط روی هذلولی بهترتیب برابر با و است. حال نقطهای روی هذلولی با مختصات را در نظر بگیرید. در این صورت اختلاف فاصله این نقطه از دو کانون برابر است با:
اگر نقطهای از یک هذلولی باشد، در این صورت فاصلههای زیر بدست میآیند.
با توجه به تعریف هذلولی، مقدار به ازای هر مقداری از روی هذلولی، مقداری ثابت است. اختلاف این مقادیر برای نقطه برابر با مقدار ثابت است. بنابراین میتوان گفت که برای هر نقطه دلخواهی روی هذلولی، اختلاف نقاط روی هذلولی با کانونها برابر با است. توجه داشته باشید که معادله هذلولی بر اساس فاصله بدست میآید. نحوه بدست آمدن معادله هذلولی خارج از حوصله این مطلب است. نهایتا معادله هذلولی را میتوان مطابق با رابطه زیر توصیف کرد:
در رابطه فوق:
- : طول هذلولی
- : مختصات طولها
- : عرض هذلولی
- : مختصات عرضها
- طول کانون برابر با بوده و در رابطه صدق میکنند.
- : مختصات کانونها
- معادله مجانبها برابر با است.
رابطه فوق نشاندهنده هذلولی است که روی محور قرار دارد. از طرفی معادله هذلولی قرار گرفته روی محور نیز به صورت زیر قابل بیان است.
در شکل زیر هر دوی این هذلولیها نشان داده شدهاند.
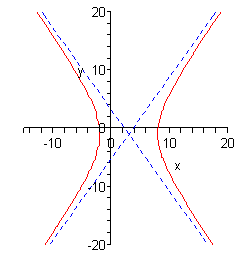
برای نمونه شکل یک هذلولی با معادله زیر در ادامه ترسیم شده است.
در صورتی که مطلب فوق برای شما مفید بوده آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضی
- مجموعه آموزشهای فیزیک
- محیط بیضی — به زبان ساده
- قضیه تالس — به زبان ساده
- تقلبنامه (Cheat Sheet) فرمولهای جبری
^^













عالی بود ممنونم از شما
با سلام و تبریک به شما بخاطر علاقه به دانش فیزیک، رکن اصلی پیشرفت هر مملکت.
گرچه به اون چیزی ک می خواستم نرسیدم اما مطالبتون خیلی خوب بود . همیشه بدرخشید و همیشه بهتر از قبل باشید:
ببخشید اگه معادله ما به صورت زیر باشد چگونه هذلولی رسم میشود?
|z_i|_|z+2i|
و این معادله برابر ۱۰ است
آیا این درسته؟هذلولی مکان هندسی نقاطی از صفحه است.که ضرب فاصله ی آنها از دو خط متقاطع(غیر منطبق)مقداری ثابت است.