حل دستگاه معادلات دیفرانسیل غیر خطی در متلب | گام به گام
در این مطلب قصد داریم تا حل دستگاه معادلات دیفرانسیل غیر خطی در متلب را بررسی کنیم. بدین منظور ابتدا مروری بر درجه معادلات و خطی و غیر خطی بودن معادلات دیفرانسیل خواهیم داشت. بعد از آن ابتدا تعریف یک تابع را در متلب بررسی میکنیم و سپس حالتهای مختلف حل معادلات دیفرانسیل در متلب را معرفی خواهیم کرد. اگر به دنبال روش حل دستگاه معادلات دیفرانسیل غیر خطی در متلب هستید این مطلب را از دست ندهید.
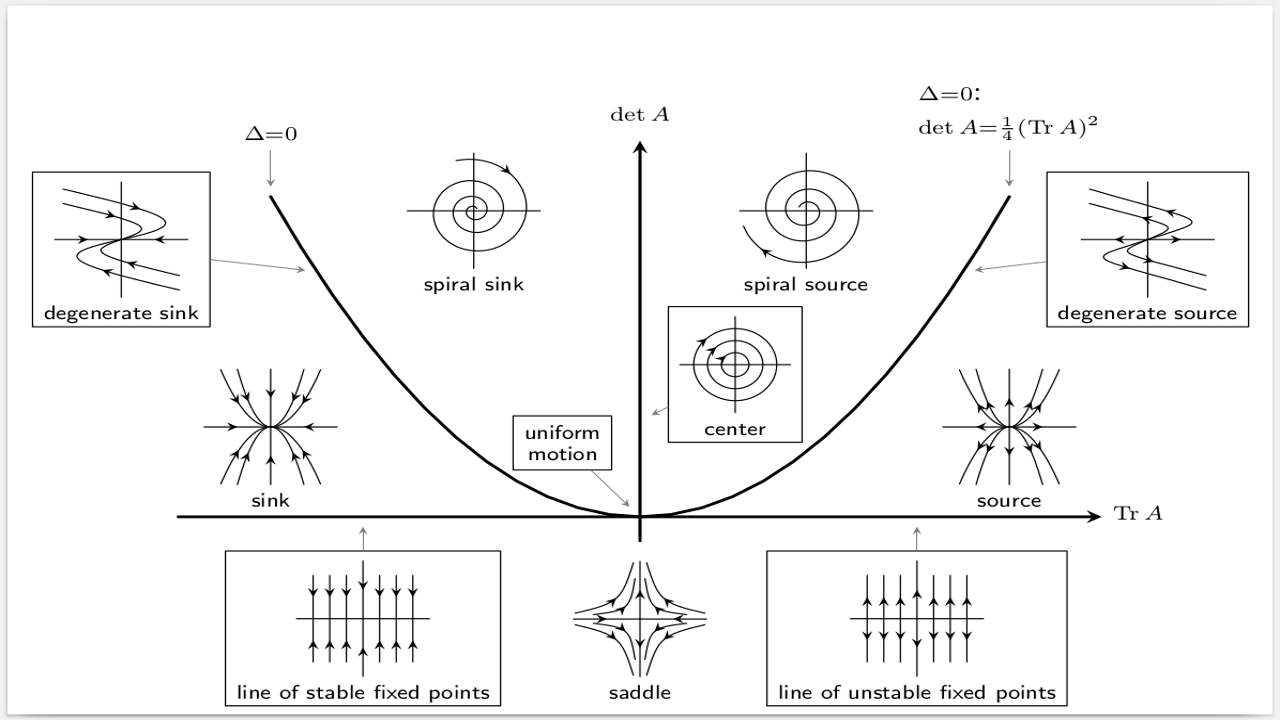

معادلات دیفرانسیل خطی و غیر خطی
ابتدا تعریفی از درجه معادلات دیفرانسیل ارائه میدهیم. درجه معادله دیفرانسیل برابر با درجه بالاترین مشتق در یک معادله است. به این ترتیب یک معادله دیفرانسیل که بالاترین درجه مشتق آن یک است، یک معادله دیفرانسیل مرتبه اول خواهد بود و در صورتی که توان متغیر بزرگتر از 1 باشد با معادلات دیفرانسیل مرتبه بالاتر روبهرو هستیم.
همچنین منظور از معادله دیفرانسیل خطی این است که متغیر در یک معادله فقط با توان یک ظاهر میشود و بنابراین خطی است اما غیر خطی است. همچنین هر تابعی مانند نیز غیر خطی است.
در ریاضی و فیزیک خطی به طور کلی به معنی ساده و غیر خطی به معنای پیچیده است. نظریات و تئوریهای حل معادلات خطی به خوبی توسعه یافتهاند زیرا معادلات خطی به اندازه کافی ساده و قابل حل هستند. اما معادلات دیفرانسیل غیر خطی معمولاً حل دقیق ندارند و موضوع تحقیقات بسیاری هستند. در ادامه شرح مختصری از نحوه تشخیص معادله خطی را بیان میکنیم.
معادله یک خط راست را در نظر بگیرید:
که در آن b و m ثابت هستند (m شیب و b عرض از مبداء است). در یک معادله دیفرانسیل وقتی متغیرها و مشتقات آنها فقط در ثابتها ضرب میشوند معادله خطی است. در یک معادله خطی متغیرها و مشتقات آنها باید همیشه به عنوان جملاتی با توان اول ظاهر شوند. چند نمونه را در ادامه بررسی میکنیم:
یک معادله خطی است، نیز خطی است. در حالی که غیر خطی است زیرا توان یک نیست. همچنین و هم غیر خطی هستند. معادله نیز غیر خطی است زیرا در یک عدد ثابت ضرب نشده است.
در توابعی با دو یا چند متغیر نیز اصل موضوع یکسان است؛ یعنی معادله خطی است، در حالی که معادله غیر خطی است.
با این مقدمه و شناخت مختصر از توابع خطی و غیر خطی، در این مطلب به حل دستگاه معادلات دیفرانسیل غیر خطی در متلب میپردازیم. بدین منظور ابتدا روش ساخت توابع در متلب را توضیح میدهیم، سپس حل معادلات پارامتری را در متلب بررسی میکنیم و پس از آشنایی با حل معادلات مرتبه اول در متلب، حل دستگاه معادلات مراتب بالاتر را در متلب مورد بررسی قرار میدهیم. در ادامه این مطلب نیز حل دستگاه معادلات غیر خطی را در متلب با چندین مثال بررسی میکنیم.
ساخت توابع در متلب
توابع در متلب در دو .m فایل جداگانه ساخته و فراخوانی میشوند. برای ساخت تابع در متلب در یک ادیتور از دستور function استفاده میکنیم و خروجیها و ورودیهای آن تابع را مشخص میکنیم.
سپس باید این فایل را ذخیره کنیم، مهمترین نکته در این مرحله که باید در نظر گرفت این است که نام تابع شما باید با نام فایل یکسان باشد. یعنی اگر نام تابع شما است فایل این تابع نیز باید باشد.
برای استفاده از این تابع باید آن را فراخوانی کنیم. بدین منظور در فایل .m دوم فایل را صدا کرده و به ورودیها مقدار میدهیم و خروجیها را مشخص میکنیم. در این مرحله لزومی ندارد که نام ورودیها و خروجیها با نام ورودی و خروجی تابع یکسان باشد. با اجرا کردن این تابع مقدار خروجیها در صفحه command window متلب نمایش داده میشوند.
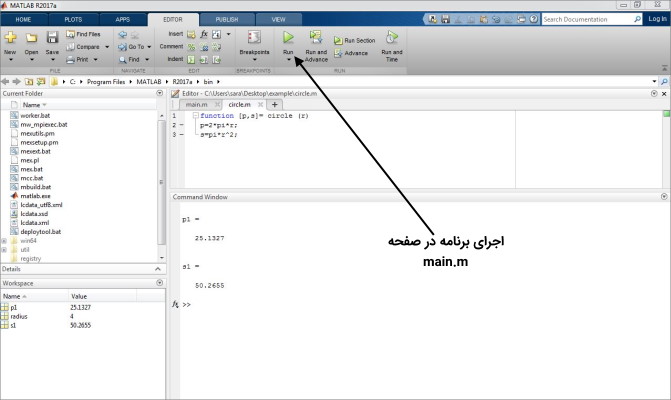
به عنوان اولین مثال فرض کنید تابعی داریم که میخواهد محیط و مساحت دایره را برای ما محاسبه کند. در این حالت خروجی تابع شما محیط و مساحت و ورودی شما شعاع دایره است. بدین منظور به صورت زیر عمل میکنیم:
نام تابعی که در اینجا انتخاب کردهایم circle است، پس تابع را نیز با همین نام یعنی circle.m ذخیره میکنیم. در این حالت خروجیهای تابع p و s و ورودی تابع r است. در مرحله بعد تابع اصلی را میسازیم و در یک ادیتور جدید به صورت زیر عمل میکنیم:
این صفحه را نیز تحت عنوان main.m ذخیره میکنیم. حالا با استفاده از گزینه Run در تابع main مساحت و محیط دایره برای شعاع 4 در command window متلب با اسامی p1 و s1 نمایش داده میشوند. دقت کنید که نام توابع ورودی و خروجی تابع main و تابع circle لزوماً نباید یکسان باشد.
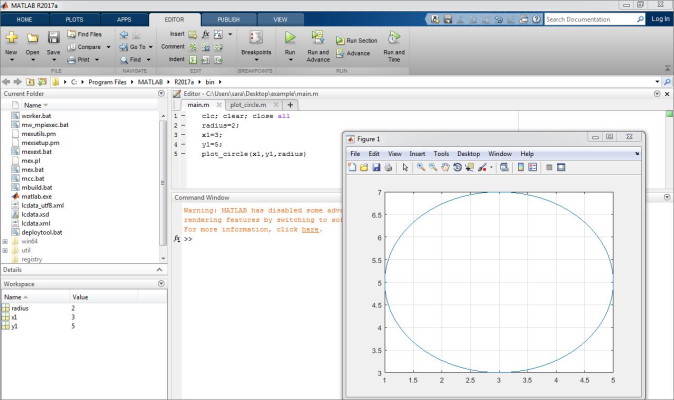
به عنوان مثال دوم میخواهیم تابعی بنویسیم که با دریافت مقادیر مختصات مرکز و شعاع یک دایره آن دایره را برای ما رسم کند. همان طور که گفتیم برای تعریف توابع از دو .m فایل استفاده میکنیم. در این حالت خروجی تابع گرافیکی است به همین منظور در این حالت از فرمت خروجی= نام تابع (ورودی) استفاده نمیکنیم و با نام تابع شروع میکنیم و داریم:
در قسمت بالا مختصات x و y دایره و شعاع را به عنوان ورودی مشخص کردیم. در خط دوم مقادیر زاویه را به صورت 100 نقطه در بازه بین تا مشخص میکنیم. حالا مقادیر x و y هر نقطه روی محیط دایره برابر با تصویر افقی و عمودی شعاع با زاویه مشخص است. در نهایت و در خط آخر دستور plot را برای مقادیر و فراخوانی میکنیم. سپس لازم است تابع main را برای این تابع بسازیم و داریم:
با اجرای تابع main دایرهای با مرکز و با شعاع 2 رسم میشود. برای اضافه کردن هر ویژگی به دستور plot آن را در فایل تابع plot_circle.m اضافه میکنیم.
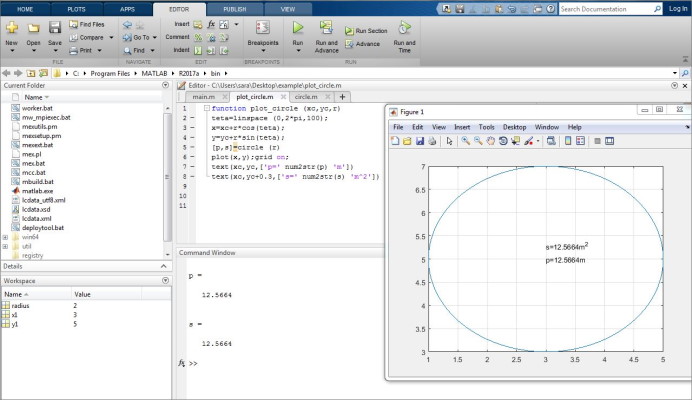
در حالت سوم میخواهیم حالتی را بررسی کنیم که از داخل تابع plot_circle تابع circle فراخوانی شود و مقادیر محیط و مساحت در مرکز این دایره چاپ شود، بدین ترتیب تنها تغییر در تابع plot_circle ایجاد میشود و داریم:
با اجرای فایل main.m خروجی به صورت زیر خواهد بود:
حل معادله مرتبه اول در متلب
در ابتدا حل عددی معادلات دیفرانسیل مرتبه اول با مشتقهای معمولی را در متلب بررسی میکنیم. همانطور که میدانید بالاترین مرتبه مشتقی که در یک معادله دیفرانسیل وجود دارد مرتبه آن معادله نامیده میشود. پس حل معادله دیفرانسیل مرتبه اول یعنی بالاترین درجه مشتق در این معادله مرتبه اول است. همچنین منظور از مشتقهای معمولی زمانی است که مشتقات بر حسب یک متغیر باشد. برای مثال معادله زیر را در نظر بگیرید:
این معادله یک معادله دیفرانسیل مرتبه اول با مشتق معمولی است. برای حل این معادله به صورت عددی در متلب نیاز به دانستن شرایط اولیه و مرزی معادله داریم. موضوع دیگری که باید آن را برای حل خود مشخص کنیم محدوده حل این معادله است، برای مثال محدوده حل معادله بالا را به صورت در نظر میگیریم. به علاوه شرط مرزی لازم برای حل این معادله را به صورت با داشتن این موارد میتوانیم معادله را در متلب حل کنیم.
برای حل این معادله دوباره به دو فایل نیاز داریم یک فایل اصلی که بازه حل و شرایط مرزی در آن مشخص میشود و یک فایل شامل خود تابع که معادله دیفرانسیل را در آن مشخص میکنیم. بدین ترتیب در فایل main.m داریم:
در قسمت بالا منظور از ode45 استفاده از روش رونگه کوتا مرتبه 4 برای حل معادله است و برای نمایش جواب نیز از دستور رسم نمودار مقادیر X بر حسب Y استفاده میکنیم. همچنین در فایل func.m نیز خواهیم داشت:
در حل نوشتن معادله دیفرانسیل در متلب دقت کنید که بالاترین درجه مشتق را در یک سمت تساوی و بقیه جملات را به سمت دیگر تساوی میبریم. همان طور که در قسمت تولید توابع در متلب گفتیم برای تعریف تابع در متلب باید تعداد خروجی و ورودی تابع را مشخص کنیم و در نهایت نمودار این تابع برای مقادیر X بر حسب Y به صورت زیر خواهد بود. همچنین مقدار تغییرات X و Y را میتوان در جداول نشان داده شده در تصویر مشاهده کرد.
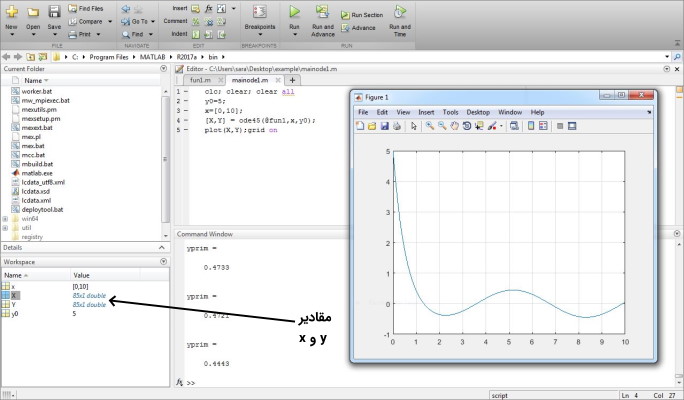
با نوشتن X یا Y در command window نیز میتوانیم مقادیر X و Y را مشاهده کنیم.
حل معادله مرتبه اول در متلب برای یک مقدار خاص
گاهی میخواهیم تابع دیفرانسیل را برای مقدار خاصی حل کنیم. برای مثال میخواهیم برای نقطه مقدار تابع را به دست آوریم. در این حالت چه کاری باید انجام داد؟ یکی از روشها این است که بازه حل را محدود به نقاطی کنیم که میخواهیم مقادیر Y را در آن نقاط به دست آوریم و تغییر زیر را در تابع main.m اعمال کنیم:
در این روش از دقت حل کم نمیشود و حل به همان طریق صورت میگیرد فقط خروجیها تنها برای مقادیر X داده شده محاسبه میشوند.
حل دستگاه معادلات مرتبه اول در متلب
گاهی ممکن است به جای یک معادله چندین معادله داشته باشیم که اصطلاحاً به این معادلات دستگاه معادلات دیفرانسیل میگوییم و میتواند شامل یک، دو یا چند معادله باشد. این معادلات به یکدیگر وابسته هستند، یعنی توابع اصلی آنها در معادلات تکرار میشوند و وجود دارند. دستگاه معادله خطی زیر را در نظر بگیرید:
به دلیل اینکه دو معادله دیفرانسیل مرتبه 1 داریم، دو شرط مرزی نیز برای حل این دستگاه نیاز است که به صورت زیر تعریف میکنیم:
و در نهایت باید محدوده حل را مشخص کنیم. با اینکه دستگاه معادلات داریم ولی چون متغیر x است پس یک محدوده حل به صورت برای حل دستگاه کافی است. باز هم همانند حالت قبل به دو .m فایل نیاز داریم. فایل تابع به صورت زیر تغییر میکند:
در حقیقت در خط دوم بیان میکنیم که یک بردار است و در خطوط بعد این بردارد را با اندیس 1 و 2 نمایش میدهیم. در این حالت تابع main.m نیز به صورت زیر تغییر میکند و داریم:
در نهایت خروجی را به صورت نمودار رسم میکنیم که به شکل زیر خواهد بود:
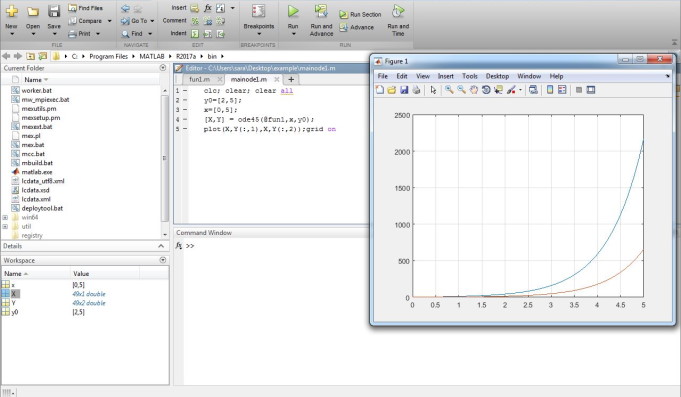
نکتهای که باید مطرح کرد این است که جوابهای Y در این حالت دو ستونی هستند و برای نمایش جوابهای Y باید شماره ستون را مشخص کرد.
خروجی این دستگاه خطی را میتوان به صورت دیگر نیز محاسبه کرد. البته این حالت تنها برای دستگاه معادلات خطی امکان پذیر است و در حالات دیگر نمیتوان از این روش استفاده کرد. در این حالت میخواهیم از فرمالیسم ماتریسی استفاده کنیم. بدین ترتیب ضرایب معادله اول را در سطر اول و ضرایب معادله دوم را در سطر دوم ماتریس قرار میدهیم و ماتریس ضرایب را ایجاد میکنیم. سپس ماتریس ضرایب را در مقدار ضرب میکنیم، بدین ترتیب داریم:
در فایل main.m نیز تغییری حاصل نمیشود و فقط نام فایل بر اساس تغییر نام فایل که در بالا انجام دادهایم به fun1b تغییر میکند. با اجرای برنامه جوابها مانند حالت قبل محاسبه میشوند.
حل معادله مرتبه بالاتر در متلب
در این قسمت در مورد حل معادلات مرتبه بالاتر در متلب صحبت میکنیم. برای این کار در ابتدا یک تغییر متغیر در معادله دیفرانسیل انجام میدهیم و سپس از دستور ode استفاده میکنیم. این تغییر متغیر سبب میشود تا معادلات مرتبه بالاتر به معادلات مرتبه اول تبدیل شوند.
طبق اصل تغییر فضای حالت میتوان یک معادله مرتبه را به معادله مرتبه یک تبدیل کرد. معادله زیر را در نظر بگیرید:
در معادله بالا برابر با مشتقات دیگر y از مرتبه تا صفر و یک متغیر مستقل است. برای تغییر متغیر از تابعی مانند z استفاده میکنیم و از y تا را تغییر متغیر میدهیم، یعنی داریم:
حال از دستگاه معادلاتی که به دست آمده مشتق میگیریم و داریم:
این معادلهای است که باید به دستور ode بدهیم تا آن را حل کند. در واقع ما دستگاه معادلهای از داریم که میخواهیم حل کنیم. حال برای حل این دستگاه n-1 شرط مرزی داریم که به صورت زیر تعریف میشوند:
با اعمال تغییر متغیر روی این شرایط اولیه نیز داریم:
حال با روشی که توضیح دادیم میخواهیم یک معادله مرتبه دو را در متلب حل کنیم که این معادله به صورت زیر است:
شرایط اولیه و بازه حل نیز عبارت است از:
با توجه به توضیحات بالا تابع در متلب به صورت زیر نوشته میشود:
این قسمت از برنامه را به عنوان تابع func4.m ذخیره کرده و تابع main.m را به صورت زیر تعریف کرده و ذخیره میکنیم:
پس از اجرای این برنامه نتایج به صورت زیر نمایش داده میشوند:
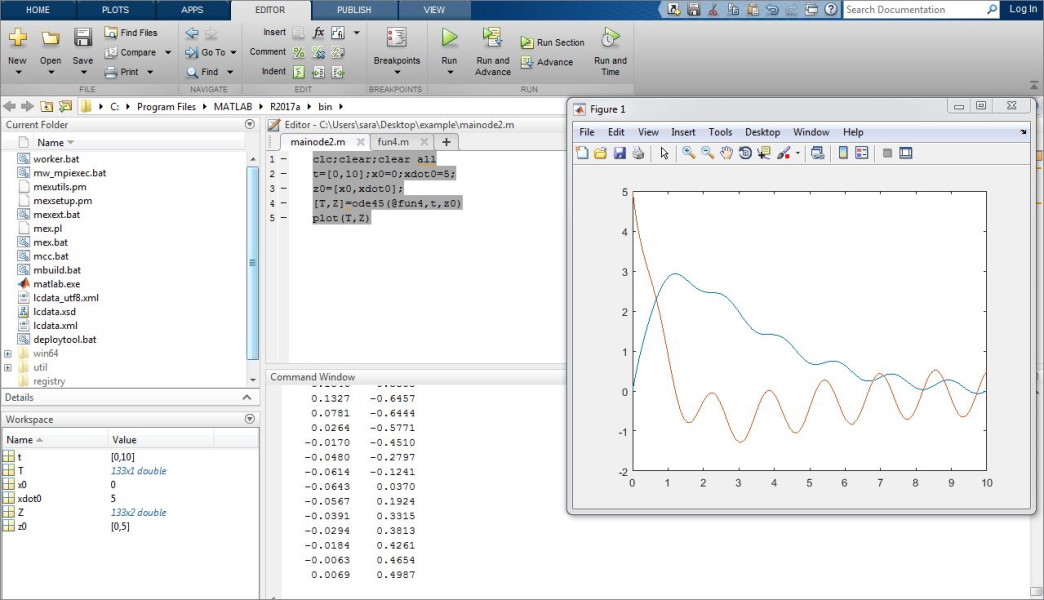
نمودار بالا تغییرات و را بر حسب نمایش میدهد. این معادله را میتوان از روش ماتریسی نیز حل کرد و داریم:
و با اجرای فرم ماتریسی نیز خواهیم دید که جوابها شبیه به حالت قبل محاسبه میشوند. برای حالت بعد فرض کنید که ضرایب ثابت را با پارامتر نمایش دهیم، برای مثال ضریب را با ، ضریب را با و ضریب را با نمایش میدهیم. در این صورت فرم تابع در متلب به صورت زیر خواهد بود:
و با اجرای تابع main.m به همان جواب حالت اول میرسیم. با قرار دادن ضرایب به صورت پارامتری به راحتی میتوان با تغییر پارامترها حالتهای مختلفی را بررسی کرد و نیازی به اعمال تغییرات در کل کد نیست. مقدار این پارامترها را میتوان در فایل main.m مقداردهی کرد و در فایل تابع تنها پارامترها را تعریف کنیم. برای این موضوع از دستور global استفاده میکنیم و تغییرات در دو فایل تابع و main به صورت زیر خواهد بود:
با اجرای این برنامه باز هم میتوان نتایج را به ازای پارامترهای مختلف برای و مشاهده کرد.
حل معادلات دیفرانسیل غیر خطی در متلب
همانطور که در ابتدای این مطلب بیان کردیم، معادله غیر خطی معادلهای است که در آن توان متغیرها متفاوت از یک باشد یا ضریب متغیر ثابت نباشد. برای بررسی این حالت معادله زیر را در نظر بگیرید:
در معادله بالا است. معادله بالا یک معادله غیر خطی و درجه دو است. از روشی که در قسمت قبل بیان کردیم معادله درجه دو را به 2 معادله درجه 1 تبدیل میکنیم و بدین ترتیب داریم:
بدین ترتیب اگر باشد فایل تابع در متلب به صورت زیر خواهد بود:
و فایل main.m نیز برابر است با:
با اجرای برنامه تغییرات و به صورت زیر خواهد بود:
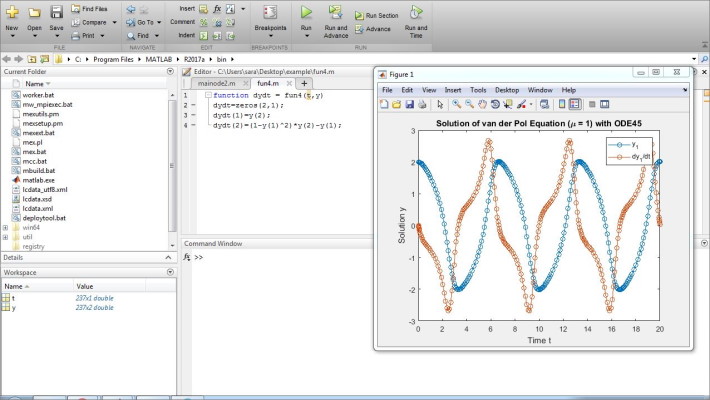
حل دستگاه معادلات دیفرانسیل غیر خطی در متلب
به عنوان آخرین بخش در این مطلب میخواهیم حل یک دستگاه معادلات غیر خطی را در متلب بررسی کنیم. بدین منظور دستگاه زیر را در نظر میگیریم:
برای حل این دستگاه معادلات دیفرانسیل غیر خطی در متلب از تغییر متغیر استفاده میکنیم. یک بردار y به صورت سه ستون مربوط به ، و در نظر میگیریم و در نتیجه دستگاه بالا به صورت زیر در میآید:
در نتیجه قسمت تعریف تابع در متلب به صورت زیر به دست میآید:
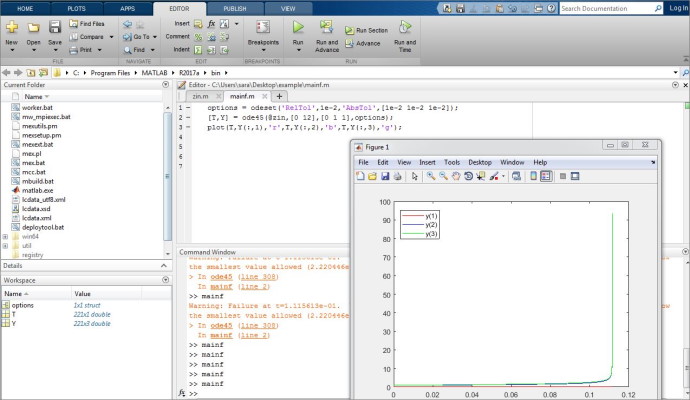
قسمت اجرایی تابع را نیز با توجه به محدوده حل و شرایط اولیه مسئله به صورت زیر تعریف میکنیم و داریم:
و در نهایت با اجرای برنامه تغییرات سه تابع ، و به صورت زیر نمایش داده میشوند:
جمعبندی
در این مطلب به معرفی و بررسی ویژگیهای متلب برای حل معادلات دیفرانسیل پرداختیم و نشان دادیم چگونه میتوان در متلب معادلات را تعریف کرد. سپس به حل معادلات به صورت عددی در متلب پرداختیم. در ادامه معادلات دیفرانسیل مرتبه یک و مراتب بالاتر را در متلب مورد بررسی قرار دادیم و حل دستگاه معادلات را نیز بررسی کردیم و نشان دادیم چگونه میتوان مقدار معادله را برای یک مقدار خاص محاسبه کرد. در انتها نیز روش حل دستگاه معادلات دیفرانسیل غیر خطی در متلب را آموزش دادیم.













فرادرس قربونت برم.
ممنون از زحماتتون
از مطالب استفاده کردم.