طول موج چیست؟ – به زبان ساده
در این مقاله در نظر داریم تا با زبانی ساده، بیشتر به بررسی مفهوم طول موج (wavelength) بپردازیم.

در مقاله «فرکانس -- به زبان ساده» با مفهوم فرکانس یک موج آشنا شدید. همچنین دیدید که فرکانس به واسطه رابطه زیر ارتباط نزدیکی با طول موج دارد.
(1)
طول موج (Wavelength)
به بیانی ساده، در فیزیک طول موج را دوره مکانی یک موج متناوب تعریف میکنند. در واقع، طول یا مسافتی که یک موج دوباره تکرار میشود را طول موج میگویند. برای روشن شدن مفهوم این جمله، به شکل زیر دقت کنید:
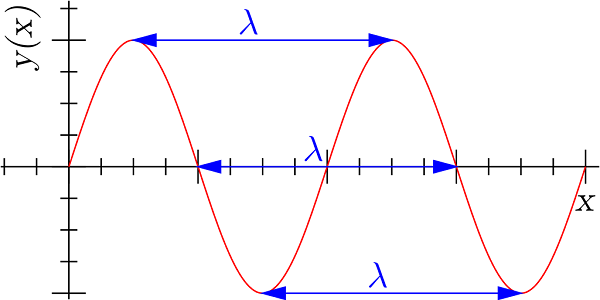
با توجه به تعریف فوق، مشخص است که طول موج، معکوس فرکانس مکانی (فضایی) بوده که غالباً به عدد موج موسوم است.
(2)
با توجه به شکل (۱)، طول موج با در نظر گرفتن فاصله بین دو نقطه متناظر، نظیر دو قله یا دو دره یا ابتدا و انتهای یک دوره تناوب، مشخص میشود. طول موج مشخصهای مهم از امواج (رونده یا ایستاده) است که در فیزیک و علوم مهندسی با نماد λ و واحد متر سنجیده میشود.
در علوم مهندسی، غالباً طول موج را برای امواج سینوسی که ظاهری یک دست دارند (همانند شکل ۱)، استفاده میکنند. اما در حالت کلی، به یاد داشته باشید که طول موج برای هر نوع موجی که به طور متناوب تکرار میشود، قابل استفاده است (شکل ۲).
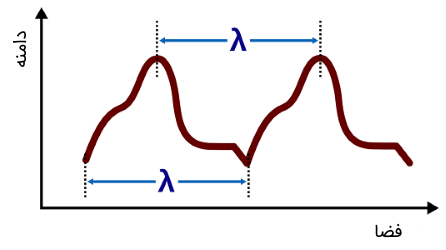
به دلیل راحتی کار با امواج سینوسی، به خصوص در کاربردهای مهندسی، غالباً امواج را سینوسی شکل در نظر گرفته و تفسیر میکنند. یکی از مزیتهای مهم امواج سینوسی که با سرعت ثابتی در حال حرکت هستند، این است که در این امواج، طول موج با معکوس فرکانس متناسب است.
(3)
نکتهای که در اینجا باید به آن توجه کنید، این است که افزایش دامنه یا میرایی (Damping) موج ارتباطی به تغییر فرکانس یا طول موج ارتباط ندارد. به طور مثال اگر موجی با گذر زمان، میرا شود (انرژی خود را تماماً به محیط منتقل کند) تنها دامنه آن کم میشود. این امر در شکل (۳) نشان داده شده است.
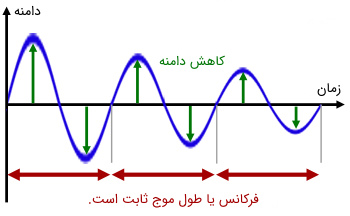
از رابطه (۳) واضح است که امواج با فرکانس بالا، طول موج کوتاهتر و امواج با فرکانس پایین، طول موج بلندتری خواهند داشت. این مطلب به وضوح در طیف امواج الکترومغناطیسی مشخص است. لازم به ذکر است که به دامنه یا محدوده تغییرات طول موج یا فرکانس امواج مختلف، طیف (spectrum) میگویند. به طور مثال طیف طول موجی امواج الکترومغناطیسی در محدوده است. لازم به ذکر است که رابطه (۳) برای امواج الکترومغناطیسی که در هوا فضای آزاد (یا با تقریب هوا) منتشر میشوند، به صورت در میآید که در آن سرعت نور در خلأ است.
پیشنهاد میکنیم، جهت آشنایی بیشتر با محدوده فرکانسی و طول موجی ناحیههای مختلف از طیف الکترومغناطیسی، به مقالات زیر مراجعه فرمایید:
- امواج رادیویی -- به زبان ساده
- امواج مایکروویو (Microwave) یا ریزموج -- به زبان ساده
- مادون قرمز (Infrared) -- به زبان ساده
- ناحیه مرئی -- به زبان ساده
- تابش ترمزی و اشعه ایکس -- به زبان ساده

طیف فرکانسی امواج مکانیکی صوتی نیز به شکل زیر است:

محدوده شنوایی انسان بر حسب طول موج، به راحتی به وسیله رابطه (۳)، قابل محاسبه است. لازم به ذکر است که سرعت صوت در هوا (دما و فشار استاندارد ترمودینامیکی) حدود 343 متر بر ثانیه است. پس طبق رابطه (۳) داریم:
(4)
(5)
همانطور که در بالا ملاحظه کردید، طول موج امواج صوتی با فرکانس بالا، کوچکتر است. طول موج در حالت کلی پارامتر ثابتی نبوده و بستگی به محیطی دارد که موج در آن منتشر میشود. به طول مثال برای یک موج الکترومغناطیسی، طول موج در خلأ یا هوا با طول موج در یک محیط مادی که با خواص بنیادی ضریب نفوذپذیری الکتریکی و مغناطیسی، ضریب شکست ، امپدانس و ... مشخص میشود، متفاوت است.
همانطور که بیان کردیم، عبارت طول موج را برای هر نوع موجی میتوانیم استفاده کنیم. نمونههایی از امواج با ماهیتهای مختلف در زیر آمده است:
- امواج صوتی: حاصل تغییرات فشار در هوا (نمونهای از موج مکانیکی)
- امواج الکترومغناطیسی: حاصل تابش ذرات باردار شتاب دار (میدانهای الکتریکی و مغناطیسی عمود برهم)
- سیگنال جریان متناوب: حاصل منبع ولتاژی که با زمان تغییر میکند.
- موج دریا: حاصل تغییرات ارتفاع آب (نمونهای از موج مکانیکی)
- ارتعاشات شبکه کریستالی: حاصل تغییر موقعیتهای اتمهای ساختار بلوری (جامد)
دقت داشته باشید که طول موج تنها فاصله بین دو قله یا دو دره در یک موج متناوب است (شکل ۱ و ۲) و معیاری جهت اندازهگیری میزان جابهجایی نیست. به طور مثال در امواج سینوسی شکل دریاها، میزان جابهجایی یک ذره که روی سطح آب است، به میزان شعاع دایرهای است که در سطح آب منتشر میشود (امواج سطحی).

امواج سینوسی (Sinusoidal Waves)
در محیطهای خطی، امواج مختلف را میتوان به صورت سینوسی در نظر گرفت. همانطور که در رابطه (۳) بیانکردیم، طول موج λ موجی سینوسی که با سرعت ثابت در حال حرکت است، به صورت زیر با فرکانس موج ارتباط دارد.
(6)
سرعت ، در واقع سرعت فاز موج است. در محیطهای پاشنده، سرعت فاز به فرکانس (طول موج) بستگی داشته که این امر باعث میشود در محیطهای غیرخطی، رابطه بین فرکانس و طول موج غیرخطی باشد. این رابطه غالباً توسط رابطهای موسوم به رابطه پاشندگی (برای امواج الکترومغناطیسی) بیان میشود. به طور کلی داریم:
(7)
(8)
(9)
(10)
در مورد امواج الکترومغاطیسی که در خلأ یا هوا () منتشر میشوند، سرعت فاز موج، همان سرعت ثابت نور با مقدار است. در نتیجه یک رابطه خطی میان فرکانس و طول موج برقرار است.
به عنوان مثالی دیگر، سرعت فاز امواج صوتی در هوا (دمای اتاق و فشار اتمسفر) در حدود 343 متر بر ثانیه است. پس طول موج محدوده شنوایی انسان (Hearing range) بین 17 میلیمتر تا 17 متر است. احتمالاً شنیدهاید که خفاشها با استفاده از امواج فراصوت (فرکانسهای بالاتر از 20 کیلو هرتز) مسیر خود را مشخص میکنند. با توجه به نکته فوق، طول موج امواج فراصوت کوتاهتر از 17 میلیمتر بوده و در نتیجه خفاشها اجسام خیلی کوچک را نیز تشخیص میدهند.
امواج ایستاده (Standing Waves)
در مقاله «موج ایستاده — به زبان ساده» به طور کامل با امواج ایستاده آشنا شدید. همانطور که از نام این امواج برمیآید، منتشر نمیشوند. اگر طنابی را که دو سر آن ثابت است را تکان دهیم، توانستهایم موجی ایستاده ایجاد کنیم. در واقع یک نقطه ثابت روی طناب، به جلو نمیرود (منتشر نمیشود) و تنها بالا و پایین میشود.
شکل زیر را میتوان دو دیواره یک موجبر (Waveguide) در نظر گرفت که شرایط مرزی آن در دیوارهها، ایجاب میکنند که دامنه موج الکترومغناطیسی در دیوارهها صفر باشد (فرض کنید که موجبر فلزی و برای فرکانسهای مایکروویو ساخته شده باشد). در این صورت میتوان نشان داد که امواج الکترومغناطیسی بین دو دیواره موجبر به منزله امواج ایستاده است.
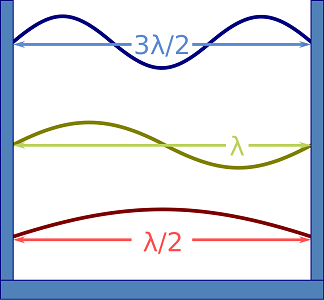
یک موج ایستاده را میتوانیم با دو موج رونده یکسان که در خلاف جهت یکدیگر هستند، نیز ایجاد کرد. به تصویر متحرک زیر دقت کنید. به طور مثال، سرعت نور را میتوان از ایجاد و مشاهده امواج ایستاده در یک جعبه فلزی، نظیر موجبر بسته یا کاواک که درون آن خلأ باشد، تعیین کرد.

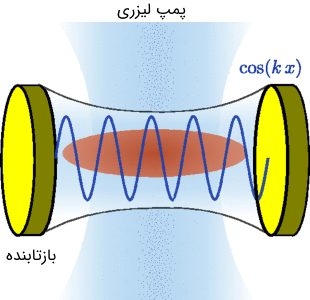
در خصوص تقویت نور حاصل از گسیل القایی در میزرها و لیزرها که در محیطی موسوم به کاواک انجام میشود، موجی که بین دو بازتابنده مدام در حال بازتاب است را میتوان به منزله موجی ایستاده در نظر گرفت.
نمایش ریاضی
یک موج رونده سینوسی را که با سرعت در حال حرکت است، را میتوان به صورت زیر نمایش داد.
(11)
در رابطه فوق، مقدار موج در موقعیت مکانی و زمانی با حداکثر مقدار (دامنه) است. در اغلب اوقات موج را به وسیله فرکانسهای زاویهای ω و مکانی به صورت زیر توصیف میکنند:
(12)
که در آن:
(13)
(14)
البته در حالت کلی (۳ بعدی)، عامل را به صورت برداری یعنی مینویسند.
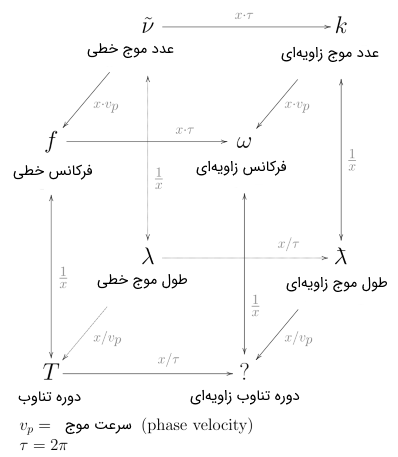
به کمک شکل زیر، میتوانیم رابطه بین پارامترهای مهم مربوط به امواج که در فیزیک به وفور از آنها استفاده میشود را به دست آوریم.
سرعت امواج الکترومغناطیسی
در مقاله «ضریب شکست -- به زبان ساده» دیدیم که سرعت یک موج الکترومغناطیسی به محیطی که در آن منتشر میشود، یعنی ضریب شکست محیط بستگی دارد:
(15)
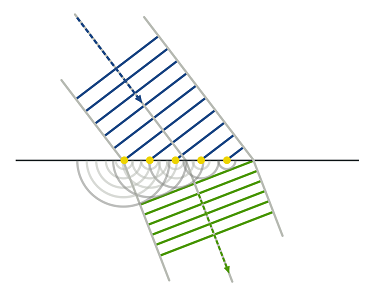
رابطه فوق بدین معنی است که اولاً سرعت امواج الکترومغناطیسی در محیطهای مادی، کمتر از سرعتشان در خلأ بوده و دوماً طول موج متناظر با فرکانس، در یک محیط مادی کوتاهتر میشود. به شکل زیر دقت کنید.
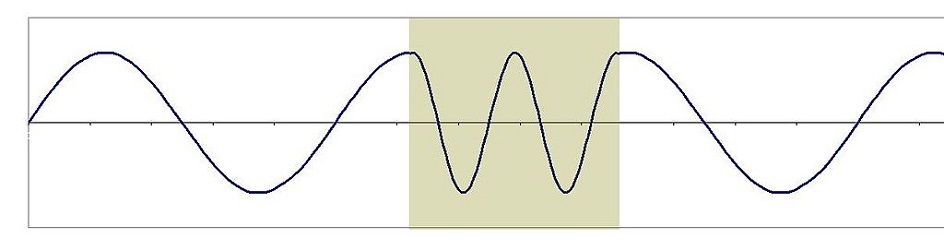
توجه داشته باشید که فرکانس موج پارامتر ثابتی است. اما سرعت و طول موج میتوانند تغییر کنند. با توجه به شکل (11)، ملاحظه میکنید که فرکانس موج که به مفهوم تکرار یک رخداد در واحد زمان است، ثابت مانده است. اما موج در محیط مادی جمعتر شده که منزله تغییر طول موج است.
تغییر در سرعت نور و در نتیجه تغییر در طول موج، به دلیل ضریب شکست محیط است. به عبارتی وقتی موجی الکترومغناطیسی از هوا با ضریب شکست تقریبی ۱ به محیطی با ضریب شکست وارد میشود، دچار شکست میشود. میزان شکست موج بر اساس رابطه اسنل (Snell's law) قابل تحقیق است (رابطه 16).
(16)
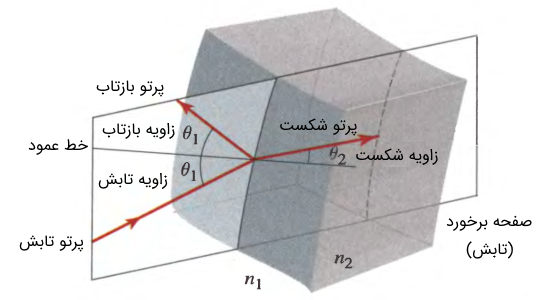
رابطه فوق بیان میکند که اگر موج الکترومغناطیسی تحت زاویه به مرز مشترک دو محیط و برخورد کند (موج ابتدا در محیط است)، تحت زاویه دچار شکست میشود. از دیدگاه اپتیک پرتو (Ray Optic) این امر را میتوان به صورت زیر نشان داد.
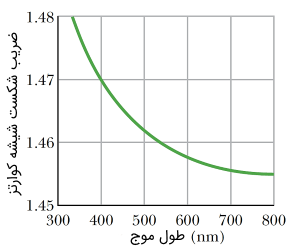
همانطور که پیشتر اشاره کردیم، در حالت کلیتر، ضریب شکست یک محیط تابعی از طول موج است (رابطه 15). در واقع ضریب شکست محیط، عددی ثابت نبوده و برای طول موجهای مختلف طیف الکترومغناطیسی متفاوت است. از این مطلب نتیجه میگیریم که سرعت مولفههای مختلف یک موج الکترومغناطیسی با یکدیگر متفاوت است. یعنی طول موجهای مختلف با سرعتهای مختلفی داخل یک محیط منتشر میشوند. تغییر در سرعت نور با طول موج خلأ را پاشندگی میگویند.

با توجه به شکل فوق، میتوان گفت که جداسازی رنگهای نور سفید که به معنی پاشندگی نور توسط منشور است، به این دلیل رخ میدهد که رنگهای مختلف با طول موجهای مختلف، ضریب شکست متفاوتی را از منشور میبینند.
در رابطه (۱۵)، سرعت نور در خلأ و ضریب شکست در طول موج است. نیز طول موجی است که در خلأ اندازه گیری شده است. پس برای یک موج الکترومغناطیسی، طول موج در محیطی با ضریب شکست برابر است با:
محیطهای غیر یکنواخت (Nonuniform Media)
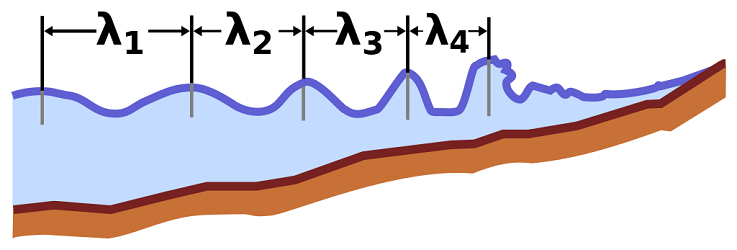
عبارت طول موج در برخی جاها، حتی برای حالتی که موج به صورت متناوب نباشد نیز به کار میرود. به طور مثال در بررسی امواج دریا در نزدیکی ساحل (شکل 16)، موجی که به سمت ساحل میآید دارای طول موجهای محلی (local wavelength) مختلفی است که به عمق آب بستگی دارند. در اینجا بررسی موجهای نزدیک ساحل بر اساس مقایسه طول موجهای محلی با عمق آب محلی صورت میگیرد.
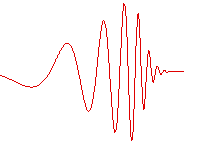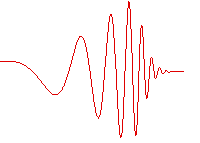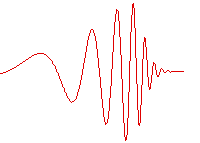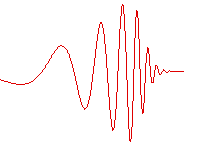
مثال دیگری از محیطهای غیر یکنواخت، محیطهای ناهمگن (inhomogeneous) بوده که در آن سرعت موج تابعی از مکان در آن محیط است. امواج سینوسی که به این دست از محیطها وارد میشوند، شکل سینوسی خود را از دست داده و ممکن است که در اثر کاهش انرژی از بین بروند. به طور مثال، شکل زیر انتشار موجی که در ابتدا سینوسی بوده است را در محیطی غیریکنواخت نشان میدهد. ابتدا با کاهش سرعت موج، طول موج کاهش یافته و دامنه افزایش پیدا میکند. با پیشروی موج در محیط که به منزله تغییر مکان در محیط ناهمگن است، طول موج کوتاهتر و افت دامنه زیاد میشود و در نهایت موج میرا شده و از بین میرود.
کریستال (Crystal)
امواج حاصل از ارتعاشات شبکه در مواد جامد کریستالی، امواجی یکتا و پیوسته نیستند. چرا که از ارتعاشات ذرات مجزایی که در واحد شبکه چیده شدهاند، به وجود میآیند.
همانند شکل زیر ارتعاشات ذرات را میتوان با امواجی با طول موجهای مختلف توصیف کرد. طبق قرار داد معمولاً در فیزیک حالت جامد، موج با بزرگترین طول موج را به عنوان امواج حاصل از ارتعاشات شبکه کریستالی در نظر میگیرند.
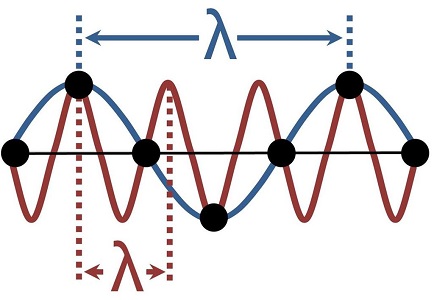
لازم به ذکر است که تمامی طول موجهایی که مطابق با شکل فوق، میتوانیم در نظر بگیریم، در مطالعه ساختار کریستالی و ترازهای انرژی اتمهای شبکه دارای اهمیت است.
زیر طول موج (Subwavelength)
اصطلاح زیر طول موج یا Subwavelength، غالباً برای توصیف ابعاد اجسامی به کار میرود که یک یا چند بعد آن از طول موج، موجی که با آن در تقابل هستند، کوچکتر باشد. به عنوان مثال، قطر فیبرهای نوری زیر طول موجی، از طول موج نوری که به درون آن کوپل میشود، کمتر است.

دقت داشته باشید که قطر فیبرهای نوری مخابراتی بیشتر از طول موج کاری بوده و لذا این فیبرها از نوع زیر طول موجی نیستند. لازم به ذکر است که طول موجهای معروف مخابراتی که در شبکههای نوری نظیر FTTX\FTTH به کار گرفته میشوند، در ناحیه مادون قرمز نزدیک قرار داشته و سه مقدار هستند.
جهت آشنایی بیشتر با طول موجهای مخابرات نوری، به مقاله «مخابرات فیبر نوری -- راهنمای جامع» مراجعه فرمایید.
در صورتی که مطلب فوق برایتان مفید بود، مطالب زیر را نیز به شما پیشنهاد میکنیم:
- مجموعه آموزشهای فیزیک
- الکترومغناطیس ۱
- مجموعه آموزشهای مهندسی برق - مخابرات
- آنتن و فرستنده -- به زبان ساده
- موجبر (Waveguide) چیست؟ — به زبان ساده
- سرعت نور و محاسبه آن از معادلات ماکسول — به زبان ساده
- پله پتانسیل (Potential Step) — به زبان ساده
^^













با سلام و عرض تشکر بابت سایت و وبلاگ عالی تان؛
چند سوال داشتم که راجع به ماهیت رنگ بنفش و نیز رنگ مجنتا (یا مگنتا – Magenta) هست:
1- این رنگهای بنفش و مجنتایی که ما در اطرافمون می بینیم (مثلا رنگ چاپی روی سفره)، طول موجشان چند است؟
2- و آیا اساساً تک رنگ هستند یا ترکیب دو رنگ آبی و قرمز هستند؟
3- آیا این رنگهای بنفش، همان بنفشی است که فرکانسش کمتر از اشعه ی ماورای بنفش است؟
4- لطفاً راجع به تفاوت (طول موج و فرکانس و قوانین ترکیب دو رنگ در) رنگهای صفحه نمایش و رنگهای روی کاغذ و رنگ روغن و آبرنگ نیز توضیح دهید.
عالی بود مثل همیشه!
دست مریزاد خیلی خیلی با حال بود
عاشق همه گونه مطالب شما هستم خدا خیرتون بده
عالی بود . ممنون دکتر …