زاویه متقابل به راس چیست؟ – به زبان ساده + حل تمرین و مثال
به زاویههای روبهرو در محل برخورد دو خط متقاطع، زاویه متقابل به راس میگویند. اندازه زاویههای متقابل به راس با هم برابر است. این زاویهها، کاربرد گستردهای در اثبات قضیههای هندسی و محاسبه اندازه انواع جفتزاویهها دارند. در این مقاله از مجله فرادرس، به معرفی زاویه متقابل به راس و کاربردهای آن در هندسه میپردازیم. ازاینرو، چندین مثال متنوع را نیز مورد بررسی قرار میدهیم.


انواع زاویه چه هستند؟
زاویهها، یکی از شکلهای پرکاربرد هندسی هستند که انواع مختلفی دارند. بیشتر زاویهها، بر اساس اندازهشان شناخته میشوند. بهعنوانمثال، جدول زیر، انواع زاویه را بر اساس اندازه نمایش میدهد.
| اندازه زاویه بر حسب درجه | عنوان زاویه |
| ۰ | زاویه صفر |
| ۰ تا ۹۰ | زاویه تند یا حاده |
| ۹۰ | زاویه راست یا قائمه |
| ۹۰ تا ۱۸۰ | زاویه باز یا منفرجه |
| ۱۸۰ | زاویه مستقیم یا نیمصفحه |
| ۱۸۰ تا ۳۶۰ | زاویه کاو، مقعر یا بازتاب |
| ۳۶۰ | زاویه کامل یا تمام صفحه |
علاوه بر اندازه، معیارهای دیگری نظیر جهت اندازهگیری زاویهها، رابطه بین جفت زاویهها و موقعیت قرارگیری زاویهها نسبت به شکلهای هندسی نیز به منظور تقسیمبندی انواع زاویهها مورد استفاده قرار میگیرد.
جفت زاویه چیست ؟
دو خط غیرمتقاطع را در نظر بگیرید. اگر خط دیگری این دو خط را قطع کند، در محل برخورد بین خطوط، درمجموع هشت زاویه به وجود میآید. تمام این هشت زاویه، به صورت دو به دو، با یکدیگر رابطه دارند. برای رابطه بین هر دو زاویه در شکل زیر، یک نام اختصاص داده میشود. این زاویهها میتوانند متناظر، متبادل خارجی، مجاور داخلی، متبادل خارجی و متقابل به راس باشند.
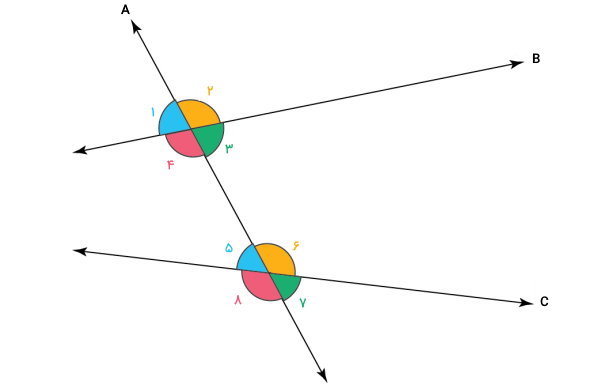
نوع جفتزاویهها، بر اساس رابطه بین اندازه آنها و محل قرارگیریشان تعیین میشود. بهعنوانمثال، زاویههای ۱ و ۵، متناظر هستند؛ در صورتی که زاویههای ۱ و ۳، دو زاویه متقابل به راس به شمار میروند. به طور کلی، جفتزاویهها، یا هماندازه هستند یا با یکدیگر زاویه ۱۸۰ درجه میسازند.
زاویه متقابل به راس چیست؟
زاویه های متقابل به راس، یکی از انواع جفتزاویهها هستند که در محل تقاطع دو خط به وجود میآیند.
تصویر زیر، زاویههای حاصل از تقاطع دو خط را نمایش میدهد. همانطور که مشاهده میکنید، در صورت عبور دو خط از روی یکدیگر، چهار زاویه در محل برخورد خطوط تشکیل میشود. به زاویههایی که روبهروی هم قرار میگیرند، «زاویه های متقابل به راس» (Vertical Angles) میگویند.
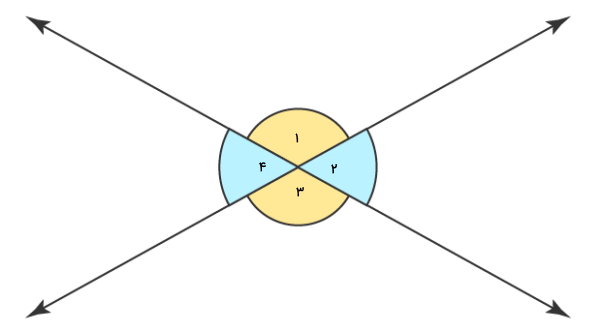
در شکل بالا، زاویههای ۱ و ۳ و زاویههای ۲ و ۴، متقابل به راس هستند.
خواص زاویه های متقابل به راس
از مهمترین ویژگی های دو زاویه متقابل به راس میتوان به موارد زیر اشاره کرد:
- زاویههای متقابل به راس، با یکدیگر برابر هستند. به عبارت دیگر، این زاویهها، همنهشت یکدیگر محسوب میشوند.
- زاویههای متقابل به راس، دارای راس مشترک هستند.
- زاویههای متقابل به راس، هیچ ضلع مشترکی ندارند.
مثال ۱: محاسبه زاویه متقابل به راس
اندازه زاویه β را به دست بیاورید.
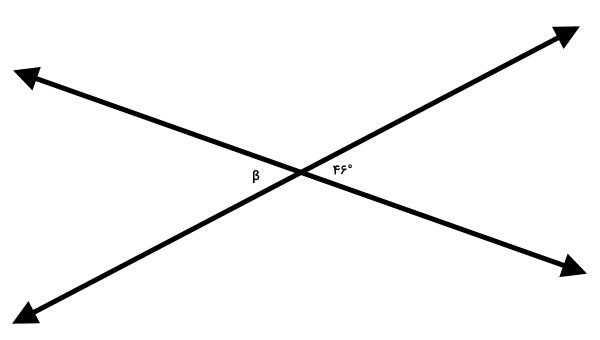
در شکل بالا، چهار زاویه وجود دارد. این چهار زاویه از برخورد دو خط تشکیل شدهاند. اندازه یکی از چهار زاویه برابر با ۴۶ درجه است. زاویه β، در مقابل این زاویه قرار دارد. بنابراین، این دو زاویه، متقابل به راس هستند. در نتیجه، اندازه زاویه β نیز برابر با ۴۶ درجه میشود.
مثال ۲: محاسبه اندازه زاویههای متقابل به راس از روی مجموع آنها
مجموع دو زاویه متقابل به راس برابر با ۱۰۶ درجه است. اندازه هر یک از این زاویهها را حساب کنید.
رابطه جمع دو زاویه مورد سوال، به صورت زیر نوشته میشود:
۱۰۶° = زاویه دوم + زاویه اول
بر اساس اطلاعات مسئله، زاویه اول و دوم، متقابل به راس هستند. بنابراین، این دو زاویه، اندازه برابر دارند. به عبارت دیگر، میتوانیم رابطه بالا را به صورت زیر بازنویسی کنیم:
۱۰۶° = زاویه متقابل به راس + زاویه متقابل به راس
۱۰۶° = زاویه متقابل به راس × ۲
۲ ÷ ۱۰۶° = زاویه متقابل به راس
۵۳° = زاویه متقابل به راس
در نتیجه، اندازه هر یک از زاویههای متقابل به راس برابر با ۵۳ درجه است.
مثال ۳: تشخیص زاویههای متقابل به راس
کدام جفتزاویه نمایش داده شده در تصویر زیر، متقابل به راس هستند.
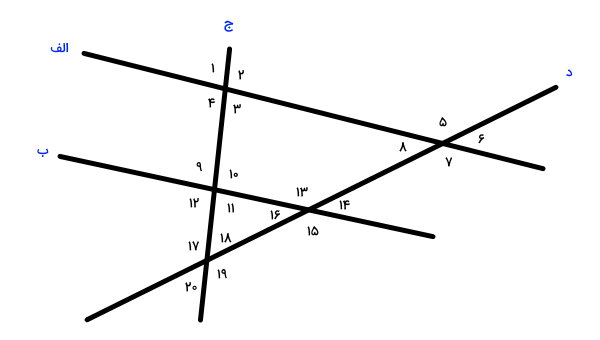
در شکل بالا، چهار خط، به گونهای همدیگر را قطع کردهاند که باعث ایجاد ۲۰ زاویه شده است. به منظور تشخیص زاویههای متقابل به راس، محل برخورد هر دو خط را مورد بررسی قرار میهیم. زاویههای روبهرویی در تقاطع خطوط، متقبل به راس هستند. بنابراین، داریم:
- زاویههای متقابل به راس در محل برخورد خط «الف» با خط «ج»
- زاویههای ۱ و ۳
- زاویههای ۲ و ۴
- زاویههای متقابل به راس در محل برخورد خط «الف» با خط «د»
- زاویههای ۵ و ۷
- زاویههای ۶ و ۸
- زاویههای متقابل به راس در محل برخورد خط «ب» با خط «ج»
- زاویههای ۹ و ۱۱
- زاویههای ۱۰ و ۱۲
- زاویههای متقابل به راس در محل برخورد خط «ب» با خط «د»
- زاویههای ۱۳ و ۱۵
- زاویههای ۱۴ و ۱۶
- زاویههای متقابل به راس در محل برخورد خط «ج» با خط «د»
- زاویههای ۱۷ و ۱۹
- زاویههای ۱۸ و۲۰
مطالب مرتبط با این مبحث:
مقایسه زاویه متقابل به راس با دیگر جفت زاویه ها
زاویههای متقابل به راس، از انواع جفتزاویههای تشکیل شده در محل برخورد دو خط است. بین این زاویه و دیگر جفتزاویهها، شباهتها و تفاوتهایی وجود دارند که در این بخش به معرفی آنها میپردازیم.
تفاوت بین زاویه مجاور و زاویه متقابل به راس
یکی از انواع زاویههایی که ارتباط بسیار نزدیکی با زاویههای متقابل به راس دارند، زاویههای مجاور هستند. جدول زیر، ویژگیهای این زاویهها و مقایسه آنها با زاویههای متقابل به راس را نمایش میدهد.
| زاویههای مجاور | زاویههای متقابل به راس |
| یک راس مشترک دارند. | یک راس مشترک دارند. |
| یک ضلع مشترک دارند. | بدون ضلع مشترک دارند. |
| لزوما با هم برابر نیستند. | حتما با هم برابر هستند. |
| در خطوط متقاطع، جمع آنها برابر با ۱۸۰ درجه میشود. | جمع آنها میتواند بین ۰ تا ۳۶۰ درجه باشد. |
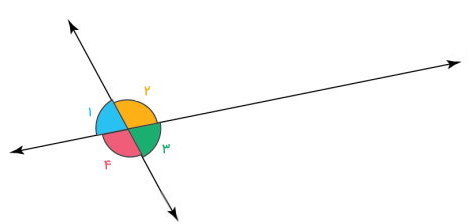
در تصویر بالا، زاویههای ۱ و ۲، زاویههای ۲ و ۳، زاویههای ۳ و ۴ و تمام زاویههایی که دارای یک ضلع و راس مشترک هستند، به عنوان زاویههای مجاور در نظر گرفته میشوند.
تفاوت بین زاویه متمم و متقابل به راس
زاویههای متمم، به زاویههایی گفته میشود که جمع آنها برابر با ۹۰ درجه باشد. این زاویهها میتوانند مجاور یا غیرمجاور (متقابل به راس، متناظر، متبادل و غیره) باشند.
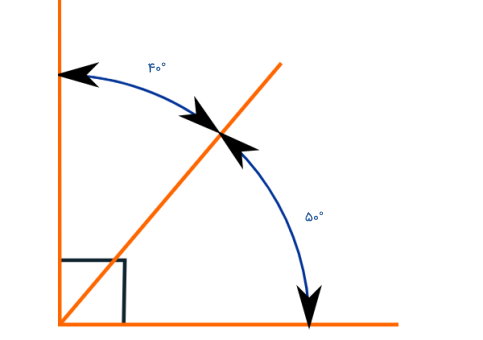
مثال ۴: محاسبه اندازه زاویههای متقابل به راس از روی متمم
دو زاویه، متقابل به راس و متمم یکدیگرند. اندازه هر زاویه چقدر است؟
اگر دو زاویه، متمم یکدیگر باشند، حاصلجمع آنها برابر با ۹۰ درجه خواهد بود:
۹۰° = زاویه اول + زاویه دوم
به دلیل متقابل به راس بودن این زاویهها، اندازه زاویه اول با زاویه دوم برابر میشود:
۹۰° = زاویه متقابل به راس + زاویه متقابل به راس
۹۰° = زاویه متقابل به راس × ۲
۲ ÷ ۹۰° = زاویه متقابل به راس
۴۵° = زاویه متقابل به راس
در نتیجه، اندازه هر زاویه برابر با ۴۵ درجه است.
تفاوت بین زاویه مکمل و زاویه متقابل به راس
اگر جمع دو زاویه برابر با ۱۸۰ درجه شود، به آنها مکمل یکدیگر میگویند. زاویههای مکمل میتوانند مجاور یا غیرمجاور باشند. در خطوط متقاطع (مانند تصویر زیر)، هر دو زاویه مجاور، مکمل یکدیگرند. به عبارت دیگر، جمع زاویههای ۵ و ۶، زاویههای ۶ و ۷، زاویههای ۷ و ۸ برابر با ۱۸۰ درجه است. زاویههای مکمل در خطوط متقاطع، یک راس و یک ضلع مشترک دارند. به علاوه، ضلعهای غیرمشترک آنها با یکدیگر، یک خط راست را تشکیل میدهند.
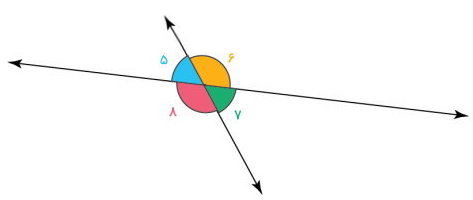
مثال ۵: محاسبه اندازه زاویههای متقابل به راس از روی مکمل
در اثر برخورد دو خط، چهار زاویه ایجاد میشود. اگر مکمل یکی از زاویهها برابر با ۶۷ درجه باشد، اندازه زاویههای سه زاویه دیگر چقدر خواهد بود؟
به منظور حل این مثال، ابتدا، مکمل زاویه ۶۷ درجه را به دست میآوریم. این زاویه عبارت است از:
۱۸۰° = ۶۷° + مکمل زاویه
۶۷° - ۱۸۰° = مکمل زاویه
۱۱۳° = مکمل زاویه
در نتیجه، دو زاویه از چهار زاویه ایجاد شده از تقاطع دو خط، برابر با ۶۳ و ۱۱۳ درجه هستند. دو زاویه دیگر، زاویههای متقابل به راس زوایای ۶۳ و ۱۱۳ را تشکیل میدهند. بنابراین، اندازه آنها نیز برابر با ۶۳ و ۱۱۳ درجه است.
در صورت تمایل به یادگیری نحوه اندازهگیری زاویهها، مطالعه مطالب زیر از مجله فرادرس را به شما پیشنهاد میکنیم:
اثبات برابر بودن زاویه های متقابل به راس
در این بخش قصد داریم ثابت کنیم زاویه های متقابل به راس با هم برابرند.
به این منظور، ابتدا دو خط متقاطع را رسم و اجزای زاویههای ایجاد شده را نامگذاری میکنیم.
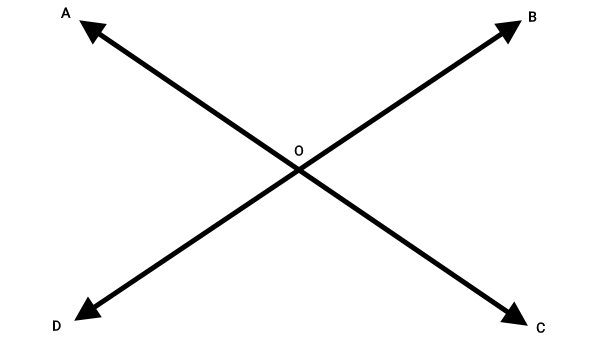
در شکل بالا، چهار زاویه با نامهای زیر وجود دارند:
- زاویه AOB
- زاویه BOC
- زاویه COD
- زاویه DOA
هدف ما، اثبات برابر بودن زاویههای روبهرویی یا همان زاویههای متقابل به راس است. در اینجا دو زاویه AOB و COD و دو زاویه BOC و DOA، روبهروی یکدیگر قرار دارند. بنابراین میخواهیم به رابطههای زیر برسیم:
اگر یکی از رابطههای بالا را اثبات کنیم، رابطه دیگر نیز اثبات میشود. طبق تعریف، زاویههای مکمل، با یکدیگر زاویه ۱۸۰ درجه میسازند. در صورت مجاور بودن دو زاویه مکمل، یک خط راست به وجود میآید. با توجه به این موضوع، میتوان مشاهده کرد که دو زاویه AOB و BOC، مکمل یکدیگر هستند.
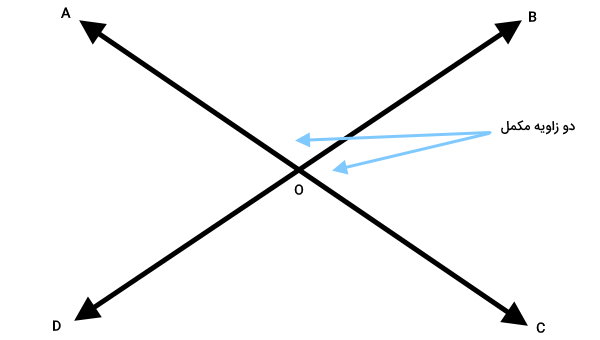
رابطه بین زاویههای AOB و BOC را مینویسیم:
به همین شکل، میتوانیم مشاهده کنیم که دو زاویه DOA و AOB نیز مکمل یکدیگر محسوب میشوند؛ چراکه ضلعهای غیرمشترک این دو زاویه، یک خط راست را تشکیل میدهند.
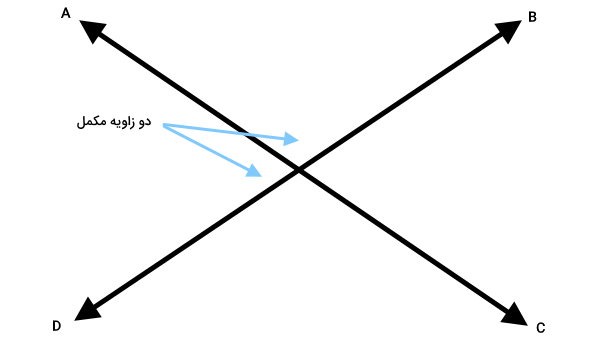
رابطه بین زاویههای DOA و AOB نیز به صورت زیر است:
روابط نوشته شده را در کنار یکدیگر قرار میدهیم:
مجموع هر دو جفتزاویه برابر با ۱۸۰ درجه است. بنابراین میتوانیم رابطه بین آنها را به صورت زیر بنویسیم:
زاویه AOB در هر دو طرف معادله قرار دارد. به همین دلیل میتوانیم آن را از هر دو طرف حذف کنیم:
در نتیجه، دو زاویه متقابل راس BOC و DOA با یکدیگر برابرند. با تکرار همین روند برای زاویههای دیگر، برابر بودن زاویههای AOB و COD نیز اثبات میشود.
زاویه های متناظر و متقابل به راس
یکی از روشهای محاسبه زاویههای متقابل به راس، استفاده از رابطه بین آنها و دیگر جفتزاویهها است. در خطوط متقاطع، به زاویههایی که از نظر موقعیت قرارگیری، مشابه یکدیگر هستند، زاویههای متناظر میگویند.
بهعنوانمثال، زاویههای ۲ و ۶ در شکل زیر، دو زاویه متناظر در نظر گرفته میشوند. زاویههای متناظر، اندازههای برابر دارند.
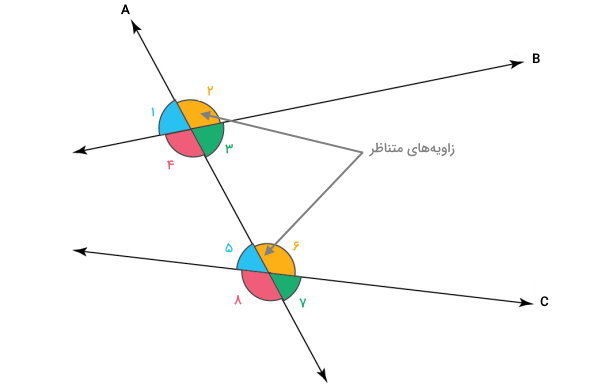
مثال ۶: محاسبه زاویه متقابل به راس از روی زاویه متناظر
اندازه زاویه e را تعیین کنید.
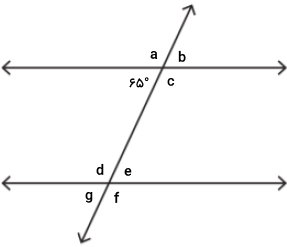
بهمنظور تعیین اندازه زاویه e میتوانیم از دو روش استفاده کنیم.
روش اول
میدانیم که زاویه e با زاویه b متناظر است. به عبارت دیگر، این دو زاویه، اندازههای برابر دارند:
از طرفی، زاویههای b و ۶۵ درجه، متقابل به راس هستند. بنابراین داریم:
به این ترتیب میتوانیم بگوییم:
روش دوم
با توجه به شکل، زاویه ۶۵ درجه با زاویه g متناظر است. از اینرو:
از طرفی، زاویههای e و g، متقابل به راس هستند:
بر اساس این دو رابطه میتوانیم بگوییم:
زاویه های متقابل به راس در چند ضلعی ها
مفاهیم مرتبط با زاویههای متقابل به راس، در رسم زاویههای خارجی چندضلعیها کاربرد دارند. زاویه خارجی، زاویهای است که بین یک ضلع و امتداد ضلع مجاور آن ایجاد میشود.
تصویر زیر، زاویههای خارجی یک چندضلعی منتظم را نمایش میدهد.
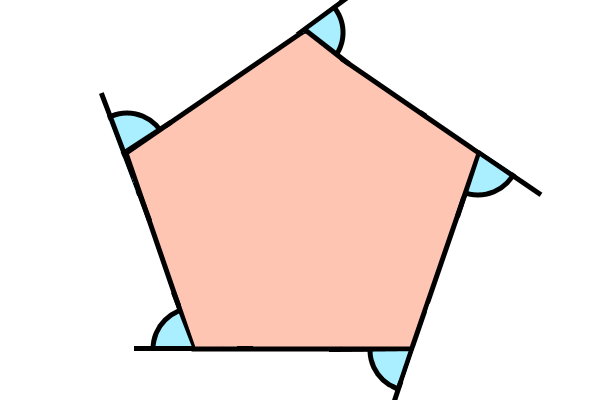
هر راس چندضلعی، از برخورد دو ضلع تشکیل میشود. در شکل بالا، اگر ضلعهای دیگر هر راس امتداد پیدا میکردند، مجدد زاویههای خارجی هر راس به وجود میآمدند (تصویر زیر). اندازه زاویههای خارجی نمایش داده شده در تصویر زیر با زاویههای خارجی نمایش داده شده در تصویر بالا با هم برابر هستند.
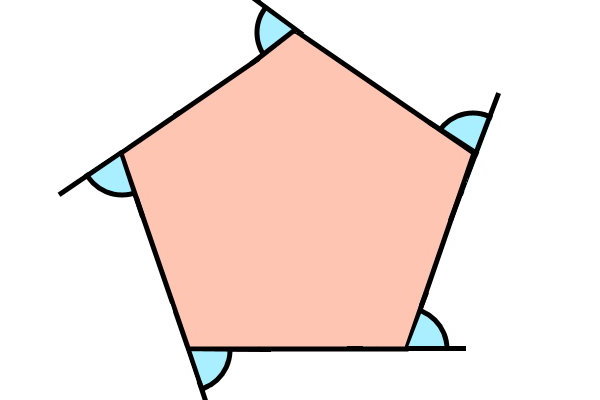
برای درک برابر بودن هر دو زاویه خارجی رسم شده از یک راس، تصویر زیر را در نظر بگیرید. در این شکل، هر دو ضلع راسها امتداد یافتهاند. به این ترتیب، دو زاویه خارجی در مجاورت هر زاویه داخلی به وجود آمده است.
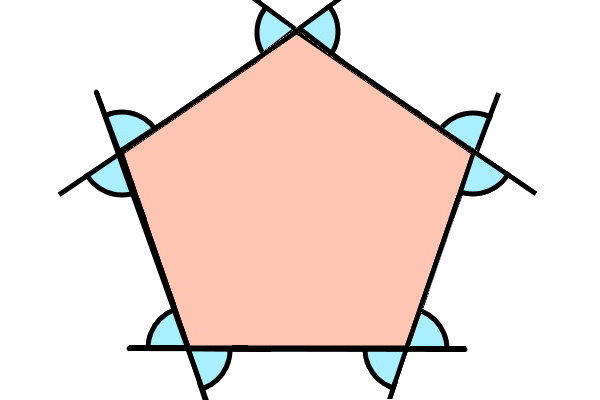
بر اساس تصویر بالا، هر دو زاویه خارجی یک راس، متقابل به راس هستند. بنابراین، تفاوتی ندارد که کدام زاویه خارجی را رسم کنیم. در هر حال، اندازه این دو زاویه با هم برابر خواهد بود. علاوه بر این، هر زاویه داخلی، با زاویه خارجی مجاورش، یک خط راست میسازد. بنابراین، زاویههای داخلی و خارجی یک راس، مکمل یکدیگرند و جمعشان برابر با ۱۸۰ درجه میشود.
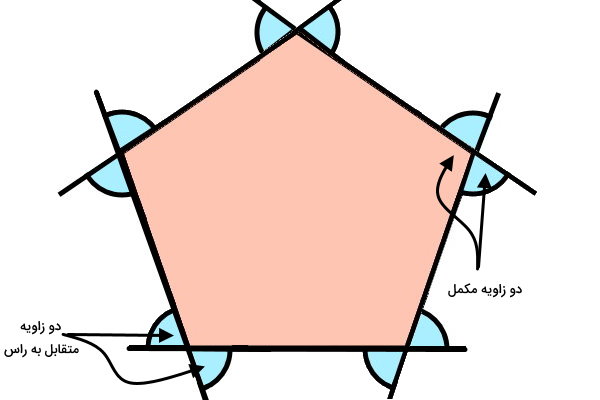
سوالات متداول در رابطه با زاویه متقابل به راس
در این بخش، به برخی از سوالات پرتکرار در رابطه با زاویههای متقابل به راس به طور مختصر پاسخ میدهیم.
تعریف زاویه های متقابل به راس چیست ؟
وقتی دو خط، همدیگر را خط میکنند، چهار زاویه درست میشود. زاویههای روبهرو، دو به دو متقابل به راس هستند.
آیا دو زاویه متقابل به راس با هم برابرند ؟
بله. زاویههای مقابل به هم در محل تقاطع دو خط، همواره مساوی هستند.
آیا جمع دو زاویه متقابل به راس برابر با ۱۸۰ درجه است؟
همیشه نه. جمع زاویههای متقابل به راس میتواند عددی بین ۰ تا ۳۶۰ درجه باشد. جمع جفتزاویههای مجاور و مکمل، برابر با ۱۸۰ درجه است.
آیا دو زاویه متقابل به راس می توانند مکمل یکدیگر باشند؟
بله. دو زاویه متقابل به راس با اندازه ۹۰ درجه، مکمل یکدیگرند.
آیا دو زاویه متقابل به راس می توانند متمم یکدیگر باشند؟
بله. دو زاویه متقابل به راس با اندازه ۴۵ درجه، متمم یکدیگرند.
هم نهشتی زاویه های متقابل به راس چیست ؟
به زاویههایی که دارای اندازه برابر باشند، زاویههای همنهشت میگویند. دو زاویه متقابل به راس، همواره همنهشت هستند.
آیا زاویه های متقابل به راس ضلع مشترک دارند؟
خیر.
کدام یک از اجزای زاویه های متقابل به راس مشترک است؟
زاویههای متقابل به راس همیشه در راس مشترک هستند.
آزمون زاویه متقابل به راس
۱. کدام ویژگی زیر باعث تفاوت اصلی زاویه متقابل به راس با جفت زاویههای مجاور میشود؟
مکمل بودن نسبت به یکدیگر
تشکیلشدن فقط موقع برخورد دو خط موازی
برابر بودن مجموع دو زاویه با ۱۸۰ درجه
نداشتن ضلع مشترک و داشتن راس مشترک
ویژگی که زاویههای متقابل به راس را از جفت زاویههای مجاور متمایز میکند این است که زاویههای متقابل به راس «نداشتن ضلع مشترک و داشتن راس مشترک» دارند. جفت زاویههای مجاور همیشه یک ضلع مشترک دارند، اما زاویههای متقابل به راس هیچ ضلع مشترکی ندارند و تنها در یک راس به هم میرسند. سایر گزینهها مانند «برابر بودن مجموع دو زاویه با ۱۸۰ درجه» یا «مکمل بودن» ویژگی زاویههای مجاور یا سایر جفت زاویهها است و «تشکیلشدن فقط موقع برخورد دو خط موازی» نادرست است، زیرا زاویه متقابل به راس در تقاطع هر دو خط بهوجود میآید، نه فقط خطوط موازی.
۲. اگر مجموع دو زاویه متقابل به راس برابر با ۱۴۰ درجه باشد، اندازه هر زاویه چند درجه است؟
۷۰ درجه
۵۰ درجه
۸۰ درجه
۶۰ درجه
زاویههای متقابل به راس اندازه یکسان دارند، پس اگر مجموعشان ۱۴۰ درجه باشد، هر زاویه برابر با نصف این مقدار است.
۳. در یک شکل با چهار خط متقاطع و تشکیل ۲۰ زاویه، برای پیدا کردن جفت زاویههای متقابل به راس باید به چه نکتهای توجه کنیم؟
زاویههایی را بیابیم که هر دو ضلعشان دقیقا موازی باشد.
زاویههایی را انتخاب کنیم که مجموعشان ۹۰ درجه شود.
هر زاویه را با زاویه کاملا روبهروی خود که راس مشترک دارند و ضلع مشترک ندارند، جفت کنیم.
فقط زاویههای مجاور یکدیگر را بررسی کنیم که مکمل هم باشند.
برای شناسایی جفت زاویههای متقابل به راس در محل برخورد خطوط، کافی است دو زاویه را بیابیم که دقیقا روبهروی هم باشند، راس مشترک داشته باشند اما هیچ ضلع مشترکی نداشته باشند؛ این ویژگی باعث میشود با بررسی موقعیت و روبهرویی هر زاویه نسبت به خط تقاطع، جفت متقابل به راس مشخص شود.
۴. زاویه متقابل به راس در چه وضعیتی تشکیل میشود؟
در صورتی که دو زاویه مجموعا ۹۰ درجه داشته باشند.
هنگام برخورد دو خط متقاطع و روبهروی هم قرار گرفتن زاویهها
زمانی که دو زاویه روی یک خط راست تشکیل شوند و مجاور باشند.
زمانی که دو زاویه با دو ضلع مشترک در یک چندضلعی باشند.
زاویه متقابل به راس فقط زمانی شکل میگیرد که دو خط یکدیگر را قطع کنند و زاویههای روبهرو نسبت به هم قرار بگیرند. این زاویهها همیشه اندازه برابر دارند..
۵. در مورد زاویههای متقابل به راس، کدام گزاره درست است؟
در هر نقطهای از صفحه ایجاد میشوند.
همیشه همنهشت هستند و اندازه برابری دارند.
مجموع آنها همیشه ۱۸۰ درجه است.
گاهی ممکن است ضلع مشترک داشته باشند.
عبارت «همیشه همنهشت هستند و اندازه برابری دارند» صحیح است، زیرا طبق تعریف و ویژگی زاویههای متقابل به راس، این زوایا همواره اندازه یکسانی دارند.
۶. در چندضلعی محدب هنگامی که زاویه خارجی از امتداد ضلع رسم میشود، زاویه متقابل به راس خارجی چه ویژگی دارد و تفاوتش با زاویه داخلی مجاور چیست؟
زاویههای خارجی متقابل به راس همیشه مکمل یکدیگرند و داخلی مجاور نصف آنهاست.
دو زاویه خارجی متقابل به راس اندازه مساوی دارند اما زاویه داخلی مجاور با آنها مکمل است.
زاویه خارجی متقابل به راس و زاویه داخلی مجاور هر دو همیشه مکمل هم نیستند.
زاویه داخلی مجاور و زاویه خارجی متقابل به راس هر دو برابرند.
عبارت «دو زاویه خارجی متقابل به راس اندازه مساوی دارند اما زاویه داخلی مجاور با آنها مکمل است» درست است. در چندضلعی محدب، هر راس با امتداد اضلاع دو زاویه خارجی متقابل به راس ایجاد میکند که برابرند؛ در حالی که زاویه داخلی مجاور جمعش با هر یک از این زاویههای خارجی برابر ۱۸۰ درجه است و بنابراین مکمل آنها به شمار میرود. از طرف دیگر، زاویههای متقابل به راس مکمل هم نیستند و زاویه داخلی هم نصف آنها نیست و با هیچیک از آنها برابر نیست.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «زاویه ها و انواع آن ها – هر آنجه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- زاویه چیست؟ — تعریف، انواع و اندازه گیری
- انواع زاویه چیست ؟ — معرفی تمام زاویه ها — به زبان ساده
- راس زاویه چیست ؟ — به زبان ساده + حل مثال تصویری
- زاویه حاده چیست ؟ — به زبان ساده + حل مثال های متنوع تصویری
- زاویه باز چیست ؟ — به زبان ساده + حل مثال های تصویری
- زاویه قائمه چیست ؟ — به زبان ساده + حل مثال های تصویری
- زاویه مکمل چیست ؟ — به زبان ساده + حل تمرین و مثال
- زاویه متمم چیست ؟ — به زبان ساده
- زاویه متقابل به راس چیست ؟ — به زبان ساده + حل تمرین و مثال(همین مطلب)
- زاویه های مکمل و متمم در هندسه — به زبان ساده
- زاویه نیمصفحه و تعریف آن در هندسه — به زبان ساده
- زاویه محاطی چیست ؟ — اثبات قضیه + حل تمرین و مثال های متنوع
- نیمساز چیست ؟ — به زبان ساده
- اندازه گیری زاویه با نقاله — به زبان ساده + مثال های تصویری
- اندازه گیری زاویه با گونیا — به زبان ساده + مثال های تصویری












