روش رانگ کوتا مرتبه چهارم (RK4) – از صفر تا صد (+ دانلود فیلم آموزش گام به گام)
در محاسبات عددی یا همان آنالیز عددی (Numerical Analysis)، «روشهای رانگ کوتا» (Runge–Kutta Methods) (روشهای رونگه کوتا نیز به آن گفته میشود) خانوادهای از روشهای تکرار شدنی «صریح و ضمنی» (Explicit and Implicit Methods) هستند. یکی از این روشها، یعنی رانگ کوتای مرتبه اول با عنوان «روش اویلر» نیز شناخته شده و از محبوبیت قابل توجهی برخوردار است. روشهای رانگ کوتا برای «گسستهسازی زمانی» (Temporal Discretization) جهت تخمین راه حلهای «معادلات دیفرانسیل معمولی» (Ordinary Differential Equations) مورد استفاده قرار میگیرند. این روشها در حدود سال ۱۹۰۰ توسط دو ریاضیدان آلمانی به نامهای «کارل رانگ» (Carl Runge) و «ویلهلم کوتا» (Wilhelm Kutta) ساخته شده است. شناخته شدهترین روش از خانواده روشهای رانگ کوتا، RK4، رانگ کوتای کلاسیک و یا روش رانگ کوتای مرتبه چهارم است که به طور خلاصه به آن روش رانگ کوتا گفته میشود. در این مطلب، به روش رانگ کوتا پرداخته شده و کد پیادهسازی آن در زبانهای گوناگون ارائه شده است. همچنین، برای درک بهتر مطلب، مثال هایی از حل معادلات دیفرانسیل با روش رانگ کوتا ارائه شده و پیادهسازی آن در زبان برنامهنویسی «متلب» (MATLAB) انجام شده است.
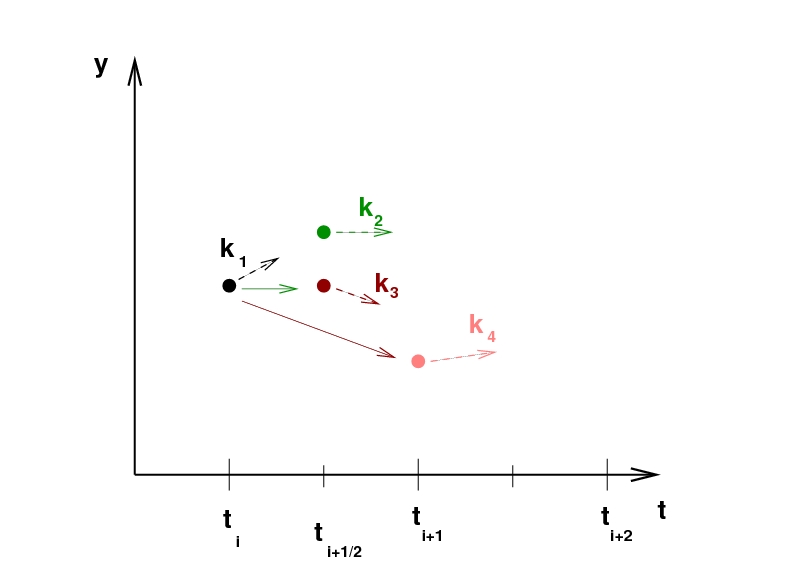
روش رانگ کوتا مرتبه چهارم
ورودیهای زیر وجود دارند:
- یک معادلات دیفرانسیل معمولی که مقدار dy/dx را به شکل x و y تعریف میکند.
- مقدار اولیه y (یعنی (0)y)
بدین ترتیب، معادله زیر وجود دارد.
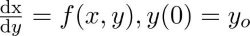
اکنون، باید مقدار تابع ناشناخته y در نقطه x را به دست آورد. روش رانگ کوتا مقدار تقریبی y برای یک x داده شده را پیدا میکند. تنها، معادلات دیفرانسیل معمولی مرتبه اول را میتوان با استفاده از روش رانگ کوتا مرتبه چهارم حل کرد. در زیر، فرمول مورد استفاده برای محاسبه مقدار بعدی yn+1 از مقدار پیشین yn به دست میآید. مقدار n برابر است. در اینجا، h طول هر گام و xn+1 = x0 + h است. طول گام کمتر به معنای صحت بیشتر است.
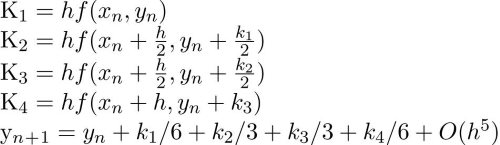
فرمول بالا اساسا مقدار بعدی yn+1 را با استفاده از yn کنونی، همراه با میانگین چهار افزایش محاسبه میکند.
- k1 افزایش بر پایه شیب در آغاز بازه با استفاده از y است.
- k2 افزایش بر پایه شیب در نقطه میانی بازه با استفاده از y + hk1/2 است.
- k3 افزایش بر پایه نقطه میانی با استفاده از y + hk2/2 است.
- k4 افزایش بر پایه شیب در پایان بازه با استفاده از y + hk3 است.
متد بیان شده در بالا، روش مرتبه چهارم است. بدین معنا که خطای برش محلی از مرتبه (O(h5 است؛ در حالی که خطای کلی تجمیع شده از مرتبه (O(h4 است. در ادامه، پیادهسازی این متد در زبانهای برنامهنویسی «پایتون» (Python)، «جاوا» (Java)، «سی» (C) و «سیپلاسپلاس» (++C)، «پیاچپی» (PHP) و «سیشارپ» (#C) ارائه شده است.
کد روش رانگ کوتا در پایتون
پیاده سازی این متد در زبان برنامه نویسی پایتون را در ادامه مشاهده میکنیم.
کد روش رانگ کوتا در جاوا
در این بخش پیاده سازی کد روش رانگ کوتا در جاوا را بررسی میکنیم.
کد روش رانگ کوتا در C++/C
در این بخش پیاده سازی کد رانگ کوتا در زبان برنامه نویسی C و سی پلاس پلاس را مشاهده میکنیم.
کد روش رانگ کوتا در PHP
در ادامه کد متد رانگ کوتا در PHP را مشاهده میکنیم.
کد روش رانگ کوتا در #C
در آخرین بخش کد روش رانگ کوتا در سی شارپ را مورد بررسی قرار میدهیم.
خروجی
در کد بالا، به ازای y=1، x=2، x0=0 و h=0.2، خروجی به صورت زیر خواهد بود. باید به این نکته نیز توجه کرد که پیچیدگی روش ارائه شده در بالا برابر با (O(n است که در آن، n برابر با x-x0)/h) است.
The value of y at x is : 1.103639
حل معادله دیفرانسیل با روش رانگ کوتا مرتبه چهارم و پیادهسازی در متلب
در ادامه، دو مثال ارائه شده است که طی آنها، یک معادله دیفرانسیل با روش رانگ کوتا مرتبه چهارم حل و پیادهسازی آن در زبان برنامهنویسی متلب انجام شده است.
مثال اول
برنامهای بنویسید که معادله دیفرانسیل زیر را با طول گام دلخواه حل کند.

حل معادله دیفرانسیل بالا با روش رانگ کوتا مرتبه چهارم و پیادهسازی آن با زبان برنامهنویسی متلب انجام شده است.
مثال دوم
برنامهای بنویسید که معادله دیفرانسیل زیر را با طول گام دلخواه حل کند.
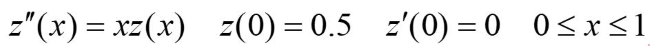
حل معادله دیفرانسیل بالا با روش رانگ کوتا مرتبه چهارم و پیادهسازی آن با زبان برنامهنویسی متلب انجام شده است.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش محاسبات عددی با MATLAB
- مجموعه آموزشهای محاسبات عددی
- آموزش ریاضی پایه دانشگاهی
- معادلات دیفرانسیل — به زبان ساده
- روش نیوتن — به زبان ساده
^^













معادلات مرتبه بالاتر رو چطور میشه به روش رانگ کوتا مرتبه4 کدنویسی متلب کرد؟
مثلا معادله نقطه سکون در سیالات که هست:
f(3) +f*f(2)-f(1)^2+1=0 ;
با سلام. من یک سوالی داشتم. برای معادله دیفرانسیل مرتبه دو باید چکار کنم؟ یعنی معادله ای به شکل زیر:
d^2(x)/dt^2+(c/m)*dx/dt+(k/m)*x
این یک معادله ارتعاشی می باشد و برابر با صفر می باشد. ممنون میشم اگر راهنمای ی بفرمایید.
سلام.
برای آشنایی با روش حل آن، پیشنهاد میکنیم به آموزش «معادلات دیفرانسیل مرتبه دوم — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
موفق باشید.
متشکر میشم کد متلبی را نیز برای آن ارسال کنید. با تشکر
سلام.
کد متلب این روش در فیلم آموزشی انتهای متن ارائه شده است.
سالم و موفق باشید.
سلام از دوستان کسی حل دستی معادله بلازیوس به روش رانگ کوتا را داره؟
سلام عالی هستیننننن خدا حفظتون کنه واقعا
چقدرم خوب درس میدین
با سلام و خسته نباشید.
ببخشید توی مثال اول اگر (y(t بشه (30-y(t یا هر عدد به جای 30 اونوقت باید چکار کنیم.
سلام کاش برا معادله دیفرانسیل مرتبه سوم هم میزاشتین خیلی بدردم میخوره
و برای شرایط مرزی اگه 0=(بینهایت)”y بجای 0=(0)”y بدن چی میشه؟
ممنون میشم بگین
سلام. برای یادگیری روش حل معادله دیفرانسیل مرتبه سوم، پیشنهاد میکنیم دو مطلب «روش اویلر — از صفر تا صد (+ دانلود فیلم آموزش گام به گام)» و «روش رانگ کوتای مرتبه دوم — از صفر تا صد» را مطالعه کنید.
از همراهیتان با مجله فرادرس خوشحالیم.
سلام.
کد متلب نمونه مثال شما رو اماده کردم .
انشالله که مفدی واقع بشه.
%% Runge Kutta method
clc
clear all
close all
%% Driver method
x0 = 0;
y = 1;
x = 2;
h = 0.2;
y = rk4(x0, y, x, h);
xi = linspace(x0,x,(x-x0)/h);
display(sprintf(‘The value of y at x is : %f ‘, y(end)));
plot(xi,y);
xlabel(‘x’)
ylabel(‘f(x,y)’)
%% A sample differential equation
%% “dy/dx = (x – y)/2”
function f = dydx(x,y)
f = (x-y) / 2;
end
%% Finds value of y for a
%% given x using step size h
%% and initial value y0 at x0.
function f_xi = rk4(x0, y0, x, h)
%% Count number of iterations
%% using step size or step
%% height h
n = ((x – x0) / h);
%% Iterate for number
%% of iterations
y = y0;
for i = 1:n
%% Apply Runge Kutta
%% Formulas to find
%% next value of y
k1 = h * dydx(x0, y);
k2 = h * dydx(x0 + 0.5 *h,y + 0.5 *k1);
k3 = h * dydx(x0 + 0.5 *h,y + 0.5 * k2);
k4 = h * dydx(x0 + h, y + k3);
%% Update next value of y
f(i) = y;
y = y + (1.0 / 6.0) * (k1 + 2*k2 + 2 *k3 + k4);
%% Update next value of x
x0 = x0 + h;
f_xi(i) = y;
end
end
% plot([x0:h:x],f_xi);
سلام کسی معادله y’1 = y’2 _ y’3 میتونه برحسب زمان انجام بده
با سلام و تشکر بخاطر نشر مطالب علمی
کد متلب مثال بالا رو برای استفاده دوستان میزارم :
%% Runge Kutta method
%% Driver method
x0 = 0;
y = 1;
x = 2;
h = 0.2;
display(sprintf(‘The value of y at x is : %f ‘, rk4(x0, y, x, h)))
%% A sample differential equation
%% “dy/dx = (x – y)/2”
function f = dydx(x,y)
f = (x-y) / 2;
end
%% Finds value of y for a
%% given x using step size h
%% and initial value y0 at x0.
function y = rk4(x0, y0, x, h)
%% Count number of iterations
%% using step size or step
%% height h
n = ((x – x0) / h);
%% Iterate for number
%% of iterations
y = y0;
for i = 1:n
%% Apply Runge Kutta
%% Formulas to find
%% next value of y
k1 = h * dydx(x0, y);
k2 = h * dydx(x0 + 0.5 *h,y + 0.5 *k1);
k3 = h * dydx(x0 + 0.5 *h,y + 0.5 * k2);
k4 = h * dydx(x0 + h, y + k3);
%% Update next value of y
y = y + (1.0 / 6.0) * (k1 + 2*k2 + 2 *k3 + k4);
%% Update next value of x
x0 = x0 + h;
end
end