رابطه بازگشتی – از صفر تا صد

رابطه بازگشتی معادله‌ای است که اصطلاحاً از بازگشت برای ربط دادن عبارات موجود در یک دنباله یا عناصر یک آرایه استفاده می‌کند. این رابطه راهی برای تعریف یک دنباله یا آرایه برحسب عبارات خودش است. روابط بازگشتی (Recurrence Relations) کاربردهای فراوانی در زمینه‌های مختلف ریاضیات دارند؛ از جمله:

• نظریه اعداد، مانند دنباله فیبوناچی
• ترکیبات، مانند توزیع اشیاء در محل‌های مختلف
• حساب، مانند روش اویلر

روابط بازگشتی وقتی مورد استفاده قرار می‌گیرند که ارائه یک رویکرد جامع برای حل مسئله دشوار باشد. اگرچه یافتن و محاسبه عبارات با استفاده از عبارات قبلی کاری ایده‌آل نیست، اما این رویکرد را می‌توان به عنوان جایگزینی کارآمد برای محاسبات در نظر گرفت.

گاهی می‌توان یک رابطه بازگشتی را با تعریف جملات یک دنباله برحسب اندیس‌های آن و نه جملات قبلی حل کرد. با این کار می‌توان به یک فرم بسته برای هر جمله از دنباله رسید که ما را از استفاده از فرایندهای تکراری بی‌نیاز می‌کند.

تشکیل رابطه بازگشتی

روابط بازگشتی برای کاهش مسائل پیچیده به یک فرایند تکراری مبتنی بر نسخه‌های ساده‌تر مسئله به کار می‌روند. جورچین برج هانوی (Tower of Hanoi) مسئله‌ای معروف است که روابط بازگشتی در حل آن کاربرد دارند.

جورچین برج هانوی از سه میله عمودی و چندین صفحه (دیسک) دایره‌ای با اندازه‌های مختلف تشکیل شده است. هر صفحه یک سوراخ در مرکز دارد تا به راحتی از میله‌ها عبور کند.

قوانین این جورچین به صورت زیر است:

• جورچین با قرار گرفتن همه صفحه‌ها روی یک میله آغاز می‌شود. ترتیب صفحه‌ها این‌گونه است که بزرگ‌ترین آن‌ها در زیر قرار می‌گیرد و کوچک‌ترین در رو.
• هدف جورچین این است که همه صفحات در یک میله دیگر قرار داده شوند.
• هر دفعه فقط یک صفحه اجازه حرکت دارد و صفحه‌ها در هر دفعه روی میله‌‌ها قرار داده می‌شوند.
• هر صفحه را می‌توان در یک میله خالی یا روی یک صفحه بزرگ‌تر قرار داد.

عبارت $$T_ n$$ را به عنوان حداقل تعداد حرکت‌های لازم برای حل یک جورچین با $$n$$ صفحه تعریف می‌کنیم. مشخص نیست که یک راه‌حل بازگشتی برای این مسئله کارگشا باشد. با وجود این، مواردی درباره مسئله وجود دارد که آن را یک گزینه مناسب برای حل با رابطه بازگشتی قرار می‌دهد.

تعریف یک مسئله برای حل با استفاده از رابطه بازگشتی به صورت زیر است:

• مسئله را می‌توان به نسخه‌های ساده‌تر کاهش داد.
• مقدار عددی $$n$$ برای شناسایی هر مورد وجود دارد. برای جورچین برج هانوی، این مقدارِ عددی، تعداد صفحات است.
• اگر مقدار عددی افزایش یابد، پیچیدگی مسئله زیاد می‌شود. وقتی تعداد صفحات در مسئله برج هانوی افزایش پیدا کند، یافتن جواب برای آن دشوارتر خواهد بود.

هدف ما در مسئله جورچین برج هانوی، یافتن رابطه بازگشتی $$T _ n$$ است. به جای تلاش برای حل یک معمای پیچیده (مانند نمونه‌ای که دارای 8 صفحه بالا است)، اغلب بهتر است با ساده‌ترین نسخه ممکن مسئله شروع کنیم.

گام ۱: تعریف یک نسخه پایه 

ساده‌ترین نسخه جورچین برج هانوی، تنها شامل یک دیسک است.

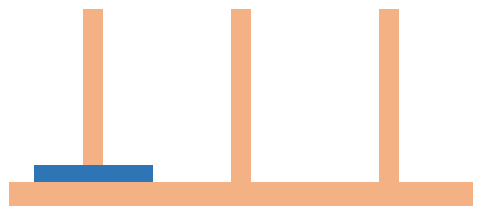
اگر بخواهیم مسئله را طبق رابطه بازگشتی بنویسم، داریم: $$n = 1$$. همچنین، $$T_ 1 = 1$$، زیرا تنها یک حرکت لازم است تا همه دیسک‌ها به میله دیگر منتقل شوند.

بدیهی است که نسخه پایه مسئله، اغلب بسیار ساده است. البته لازم است موارد پیچیده‌تر را نیز بنویسیم. حتی اگر هدف مسئله یافتن رابطه‌ای برای $$T_n$$ باشد، سریعاً نمی‌توان گفت که این معادله به چه شکلی خواهد بود. لازم است برای این کار مسئله را تکرار کنیم. بعد از آنکه دو مورد را کامل کردیم، می‌توانیم بفهیمیم که شکل رابطه بازگشتی چگونه است.

گام ۲: انجام موارد پیچیده‌تر 

شکل زیر جواب جورچین برج هانوی را برای $$n = 2$$ نشان می‌دهد.

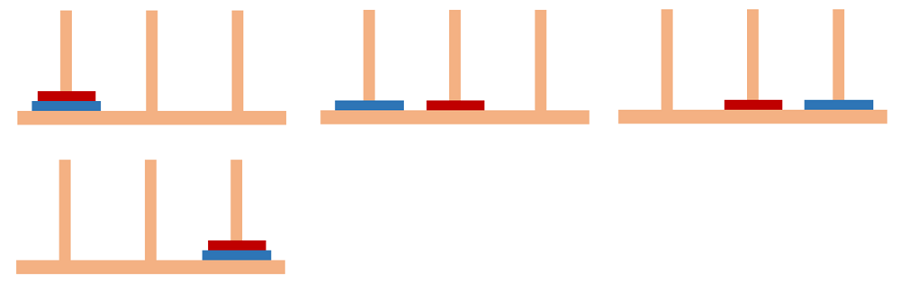
از شکل بالا در می‌یابیم که $$T_ 2 = 3$$.

جواب جورچین برج هانوی برای $$n = 3$$ نیز در شکل زیر نشان داده شده است.

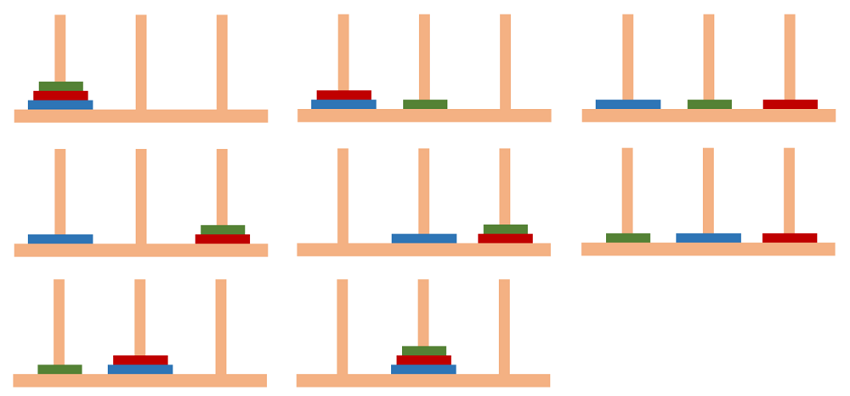
از شکل بالا مشخص است که $$T_ 3 = 7$$.

در صورت لزوم، می‌توانیم همین‌گونه ادامه داده و موارد پیچیده‌تر مسئله را بنویسیم. هدف این فرایند، فهمیدن این موضوع است که مسئله چگونه پیش می‌رود و چگونه می‌توان رابطه بازگشتی را تشکیل داد.

اگرچه در مثال بالا دو مورد را بررسی کردیم، گاهی لازم است موارد بیشتری را برای افزایش درک مسئله انجام دهیم. با مشاهده دو مورد بالا، احتمالاً می‌توانیم دریابیم که چه رابطه‌ای وجود دارد.

گام ۳: نوشتن رابطه بازگشتی

می‌خواهیم ببینیم تکرارها چه رابطه‌ای با هم دارند. در $$n = 1$$، مسئله ساده بود و با یک حرکت جورچین کامل شد. برای $$n = 2$$، دیسک کوچک‌تر را باید قبل از دیسک بزرگ‌تر جابه‌جا می‌کردیم تا امکان حرکت آن وجود داشته باشد. پس از حرکت دیسک بزرگ‌تر، دیسک کوچک‌تر را روی آن قرار دادیم و مسئله حل شد. در حالت $$n = 3$$، دیسک‌های کوچک‌تر را قبل از حرکت دیسک بزرگ‌تر جابه‌جا کردیم. پس از آن باید دیسک‌های کوچک‌تر را روی دیسک بزرگ‌تر قرار می‌دادیم تا جورچین کامل شود. اگر بخواهیم این موارد را برحسب $$n$$ بیان کنیم، داریم:

• باید تعداد $$T_ {n-1}$$ حرکت انجام دهیم تا دیسک‌های کوچک‌تر را از روی دیسک بزرگ‌تر برداریم.
• باید ۱ حرکت انجام دهیم تا دیسک بزرگ‌تر را در میله قرار دهیم.
• باید $$T _ {n-1}$$ حرکت انجام دهیم تا دیسک‌های کوچک‌تر را روی دیسک بزرگ‌تر قرار دهیم.

در کل، تعداد جابه‌جایی‌ها برای $$n$$ دیسک برابر است با:‌

$$\large T _ { n + 1 } = 2 T _ { n } + 1 .$$

می‌توان تأیید کرد که رابطه بازگشتی بالا با مقادیری که در اختیار داریم سازگاری دارد:

$$\large \begin {aligned} T _ 1 & = 1 \\ T _ 2 & = 2 T _ 1 + 1 = 2 ( 1 ) + 1 = 3 \\ T _ 3 & = 2 T_ 2 + 1 = 2 ( 3 ) + 1= 7 . \end {aligned}$$

رابطه بازگشتی مربوط به جورچین برج هانوی، مثالی از یک رابطه بازگشتی خطی است. این رابطه را می‌توان با استفاده از روش‌هایی به فرم بسته نوشت.

حل رابطه بازگشتی با توابع مولد

یک روش برای حل روابط بازگشتی استفاده از یک تابع مولد است. تابع مولد (Generating Function) یک سری توانی است که ضرایب آن متناظر با جملات دنباله‌ای از اعداد است.

مثال ۱

از تابع مولد $$T_n$$ استفاده کرده و فرم بسته $$T _ n$$ را برای مثال بالا بنویسید.

حل: رابطه بازگشتی که به دست آوردیم، به صورت زیر است:

$$\large T _ { n + 1 } = 2 T _ {n } + 1 .$$

از قبل می‌دانیم که $$T_1 = 1$$، اما لازم است مقدار $$T_0$$ را نیز بدانیم. با قرار دادن $$T_0 = 0$$ رابطه بازگشتی هنوز برقرار است.

تابع مولد زیر را تعریف می‌کنیم:

$$\large \begin {aligned} T ( x ) & = \sum \limits _ { n = 0 } ^ { \infty } T _ n x ^ n \\ \\ & = T _ 0 + T _ 1 x + T _ 2 x ^ 2 + \cdots . \end{aligned}$$

که در آن، $$T_0 = 0$$. هر دو طرف رابطه بالا را بر $$x$$ تقسیم کرده و داریم:

$$\large \begin {aligned} \frac { T ( x ) } { x } & = T _ 1 + T _ 2 x + T _ 3 x ^ 2 + \cdots \\ \\ & = \sum \limits _ { n = 0 } ^ { \infty } T _ { n + 1 } x ^ n . \end {aligned}$$

اکنون رابطه بازگشتی $$T _ { n + 1 }$$ را در معادله جایگذاری می‌کنیم:‌

$$\large \begin {aligned} \frac { T ( x ) } { x } & = \sum \limits _ { n = 0 } ^ { \infty } ( 2 T _ { n } + 1 ) x ^ n \\ \\ & = 2 T ( x ) + \sum \limits _ { n = 0 } ^ { \infty} x ^ n . \end {aligned}$$

اگر $$|x|<1$$، آنگاه یک تصاعد هندسی نامتناهی داریم که مقدار آن برابر است با:

$$\large \sum \limits _ { n = 0 } ^ { \infty } x ^ n = \frac { 1 } { 1 - x } , \ \, | x | < 1 .$$

با جایگذاری عبارت بالا، داریم:‌

$$\large \frac { T ( x ) } { x } = 2 T ( x ) + \frac { 1 } { 1 - x } , \ \, | x | < 1 .$$

حاصل $$T(x)$$ را می‌توان به صورت زیر نوشت:

$$\large T ( x ) = \frac { x } { ( 1 - x ) ( 1 - 2 x ) } , \ \, | x | < 1 .$$

اکنون فرم بسته عبارت تابع مولد به دست آمده و باید فرم بسته $$T_ n$$ را بنویسیم. از آنجایی که تابع مولد برابر با یک عبارت گویا با عوامل دوجمله‌ای در مخرج است، می‌توانیم از گسترش به کسرهای جزئی استفاده کنیم:

$$\large \begin {aligned} T ( x ) & = \frac { x } { ( 1 - x ) ( 1 - 2 x ) } \\ \\ & = x \left ( \frac { 2 } { 1 - 2 x } - \frac { 1 } { 1 -x } \right ) . \end {aligned}$$

تصاعد هندسی نامتناهی را به یاد آورید. برای گام بعدی، دو عبارت گویا را با استفاده از اتحادها به فرم سری توانی بر می‌گردانیم:

$$\large \begin {aligned} \frac { 2 } { 1 - 2 x } & = \sum \limits _ { n = 0 } ^ { \infty } { 2 ^ { n + 1 } x ^ n } \\ \\ \frac { 1 } { 1 - x } & = \sum \limits _ { n = 0 } ^ { \infty } x ^ n . \end {aligned}$$

با جایگذاری این اتحادها، داریم:

$$\large \begin {aligned} T ( x ) & = x \left ( \sum \limits _ { n= 0 } ^ { \infty } { 2 ^ { n + 1 } x ^ n } -\sum \limits _ { n = 0 } ^ { \infty } x ^ n \right ) \\ \\ & = \sum \limits _ { n = 0 } ^ { \infty } { ( 2 ^ { n + 1 } - 1 ) x ^ { n + 1 } } \\ \\ & = \sum \limits _ { n = 1 } ^ { \infty } { ( 2 ^ { n } - 1 ) x ^ { n } } . \end {aligned}$$

در نتیجه، بدیهی است که ضریب تابع مولد (سری $$T_n$$) برابر است با:‌

$$\large \boxed { T _ n = 2 ^ { n } - 1 } .$$

حل رابطه بازگشتی با عوامل مجموع‌یابی

راه دیگری برای حل روابط بازگشتی به فرم $$A a _ n = B a _ { n - 1 } + C$$ وجود دارد که در آن، $$A$$، $$B$$ و $$C$$ توابعی از $$n$$ هستند. این روش با نام روش عوامل مجموع‌یابی (Summation Factors) شناخته می‌شود. از این روش برای حل مسئله جورچین برج هانوی استفاده می‌کنیم.

مثال ۲

نشان دهید فرم بسته رابطه بازگشتی $$T_n = 2 T_{n-1} + 1$$ به صورت $$T_n = 2 ^n -1$$ است (فرض کنید $$T_0 = 0$$).

حل: عامل مجموع‌یابی $$s_n$$ با $$A(n)=1$$ و $$B(n) =2$$ برابر است با:

$$\large s _ n = \frac { 1 \cdot 1 \cdot \cdots \cdot 1 } { 2 \cdot 2 \cdot \cdots \cdot 2 } = \frac { 1 } { 2 ^ { n - 1 } } ,$$

که در آن، $$1$$ و $$2$$ به تعداد $$n-1$$ بار تکرار شده‌اند. با ضرب رابطه بالا در رابطه بازگشتی، خواهیم داشت:

$$\large \frac { 1 } { 2 ^ { n - 1 } } T _ n = \frac { 1 } { 2 ^ { n- 2 } } T _ { n - 1 } + \frac { 1 } { 2 ^ { n -1 } } .$$

فرض می‌کنیم، $$b _ n = \dfrac { 1 } { 2 ^ { n - 1 } }$$. در نتیجه، $$b _ { n - 1 } = \dfrac { 1 } { 2 ^ { n - 2 } } T _ { n - 1 }$$ و $$b _ 0 = \dfrac { 1 } { 2 ^ { 0 - 1 } } T _ 0$$. در نتیجه، خواهیم داشت:

$$\large b _ n = b _ { n - 1 } + \frac { 1 } { 2 ^ { n - 1 } } .$$

بنابراین، فرم بسته $$b_n$$ به صورت زیر خواهد بود:

$$\large b _ n = 0 + \sum _ { k = 1 } ^ n \frac { 1 } { 2 ^ { k - 1 }} = \frac { 1 \cdot \left ( \frac 1 2 \right ) ^ n - 1 } { \frac 1 2 - 1 } = 2 - \frac { 1 } { 2 ^ { n - 1 } } .$$

همان‌طور که می‌بینیم، مجموع بالا، یک دنباله هندسی متناهی است. اما از آنجایی که $$b _ n = \frac {1} {2^{n-1}} T_n$$، فرم بسته $$T_n$$ به صورت زیر خواهد بود:

$$\large T _ n = 2 ^ { n - 1 } \left ( 2 - \frac { 1 } { 2 ^ { n - 1 } } \right ) = \boxed { 2 ^ n - 1}.$$

رابطه بازگشتی خطی

یک رابطه بازگشتی خطی مرتبه $$k$$ یا درجه $$k$$، معادله‌ای بازگشتی به فرم زیر است:

$$\large x _ n = A _ 1 x _ { n - 1 } + A _ 2 x _ { n -2} + A _ 3 x _ { n - 3 } + \dots A _ k x _ { n - k }$$

که در آن، $$A_k$$ یک ثابت است و $$A_k \neq 0$$.

مثال‌هایی از معادله‌های بازگشتی خطی به شرح زیر است:

حل رابطه بازگشتی خطی

فرض کنید رابطه بازگشتی خطی مرتبه دوم $$F_n = AF_{n-1} +BF_{n-2}$$ را داشته باشیم که در آن، $$A$$ و $$B$$ اعدادی حقیقی هستند.

معادله مشخصه رابطه بازگشتی بالا به صورت زیر است:

$$\large x^2 - Ax - B = 0$$

سه حالت در یافتن ریشه‌ها ممکن است رخ دهد:

• حالت اول: اگر این معادله به صورت $$(x- x_1)(x- x_1) = 0$$ تجزیه شده و دو ریشه حقیقی متمایز $$x _ 1$$ و $$x _ 2$$ داشته باشد، آنگاه جواب $$F_n = ax_1^n+ bx_2^n$$ است که در آن، $$a$$ و $$b$$ اعداد ثابتی هستند.
• حالت دوم: اگر معادله به صورت $$(x- x_1)^2 = 0$$ بوده و داری ریشه تکراری $$x _ 1$$ باشد، آنگاه جواب $$F_n = a x_1^n+ bn x_1^n$$ است.
• حالت سوم: اگر ریشه‌های معادله، اعداد مختلط مجزای $$x _1$$ و $$x _ 2$$ به فرم قطبی $$x_1 = r \angle \theta$$ و $$x_2 = r \angle(- \theta)$$ باشند، آنگاه جواب $$F_ n = r ^ n ( a \cos ( n \theta ) + b \sin ( n \theta ) )$$ خواهد بود.

مثال ۳

رابطه بازگشتی $$F_n = 5F_{n-1} - 6F_{n-2}$$ را حل کنید که در آن، $$F_0 = 1$$ و $$F_1 = 4$$.

حل: معادله مشخصه دنباله بازگشتی به صورت زیر است:

$$\large x^2 - 5x + 6 = 0,$$

بنابراین، $$(x - 3) (x - 2) = 0$$. در نتیجه، ریشه‌های آن $$x _1 = 3$$ و $$x _ 2 = 2$$ هستند. همان‌طور که می‌بینیم، ریشه‌ها حقیقی و مجزا هستند. بنابراین، جواب برابر است با:

$$\large F_n = ax_1^n + bx_2^n$$

وقتی $$x _1=3$$ و $$x_2=2$$، آنگاه $$F_n=a3^n+b2^n$$. در نتیجه:

$$\large 1 = F _ 0 = a 3 ^ 0 + b 2 ^ 0 = a + b$$

$$\large 4 = F _ 1 = a 3 ^ 1 + b 2 ^ 1 = 3 a + 2 b$$

با حل این معادلات، جواب‌های $$a=2$$ و $$b = -1$$ را به دست خواهیم آورد.

بنابراین، جواب نهایی برابر است با:

$$\large F _ n = 2 \cdot 3 ^ n + ( - 1 ) \cdot 2 ^ n = 2 \cdot 3 ^ n - 2 ^ n$$

مثال ۴

رابطه بازگشتی $$F_n = 10F_{n-1} - 25F_{n-2}$$ را حل کنید که در آن، $$F_0 = 3$$ و $$F_1 = 17$$.

حل: معادله مشخصه رابطه بازگشتی به صورت زیر است:‌

$$\large x ^ 2 - 1 0 x - 2 5 = 0$$

بنابراین، داریم: $$(x - 5)^2 = 0$$. از آنجایی که یک ریشه تکراری داریم، جواب به صورت زیر خواهد بود:

$$\large F _ n = a x _ 1 ^ n + b n x _ 1 ^ n$$

با توجه به رابطه بالا، می‌توان معادلات زیر را نوشت:

$$\large 3 = F _ 0 = a \cdot 5 ^ 0 + b \cdot 0 \cdot 5 ^ 0 = a$$

$$\large 17 = F _ 1 = a \cdot 5 ^ 1 + b \cdot 1 \cdot 5 ^ 1 = 5 a + 5 b$$

با حل معالات اخیر، مقادیر $$a=3$$ و $$b = 2/5$$ به دست می‌آیند.

در نهایت، جواب برابر با $$F _ n = 3 \cdot 5 ^ n + ( 2 / 5 ) \cdot n \cdot 2 ^ n$$ است.

مثال ۵

رابطه بازگشتی $$F_n = 2F_{n-1} - 2F_{n-2}$$ را حل کنید که در آن، $$F _ 0 = 1$$ و $$F_1 = 3$$.

حل: معادله مشخصه رابطه بازگشتی به صورت زیر است:

$$\large x^2 -2x -2 = 0$$

ریشه‌های معادله بالا، $$x_1 = 1 + i$$ و $$x_2 = 1 - i$$ هستند. این ریشه‌ها را می‌توان به فرم قطبی $$x_1 = r \angle \theta$$ و $$x_2 = r \angle(- \theta)$$ نوشت که در آن، $$r = \sqrt 2$$ و $$\theta = \frac{\pi}{4}$$. از آنجایی که ریشه‌های معادله مشخصه مختلط هستند، جواب را می‌توان به صورت زیر نوشت:

$$\large F _ n = ( \sqrt 2 ) ^ n ( a \cos ( n \pi / 4 ) + b \sin ( n \pi / 4 ) )$$

با توجه به معادله بالا، داریم:

$$\large 1 = F _ 0 = ( \sqrt 2 ) ^ 0 ( a \cos ( 0 \pi / 4 ) + b \sin ( 0 \pi / 4 ) ) = a$$

$$\large 3 = F _ 1 = ( \sqrt 2 ) ^ 1 ( a \cos ( 1 \pi / 4 ) + b \sin ( 1 \pi / 4 ) ) = \sqrt 2 ( a / \sqrt 2 + b / \sqrt 2 )$$

با حل معادلات بالا، $$a=1$$ و $$b = 2$$ به دست می‌آید.

بنابراین، جواب نهایی برابر است با:

$$\large F _ n = ( \sqrt 2 ) ^ n ( \cos ( n \pi / 4 ) + 2 \sin ( n \pi / 4 ) )$$

رابطه بازگشتی ناهمگن

یک رابطه بازگشتی را ناهمگن می‌گوییم، اگر به فرم زیر باشد:

$$\large F _ n = A F _ { n - 1 } + B F _ { n - 2 } + f ( n )$$

که در آن، $$f(n) \ne 0$$.

رابطه بازگشتی همگن متناظر با رابطه ناهمگن بالا به صورت زیر است:

$$\large F _ n = A F _ { n – 1 } + B F _ { n - 2 }$$

جواب $$a _ n$$ یک رابطه بازگشتی ناهمگن دو بخش دارد. بخش اول، جواب $$a _ h$$ متناظر با رابطه بازگشتی همگن متناظر و بخش دوم جواب خصوصی $$a_t$$ است:

$$\large a _ n = a _ h + a _ t$$

جواب بخش اول را می‌توان با روندی که در بالا آن را توضیح دادیم، به دست آورد. اما برای یافتن جواب خصوصی، یک جواب آزمایشی را به دست می‌آوریم. فرض کنید $$f(n) = cx^n$$. با در نظر گرفتن $$x^2 = Ax + B$$ به عنوان معادله مشخصه متناظر با رابطه بازگشتی همگن و $$x _1$$ و $$x_2$$ به عنوان ریشه‌های آن،‌ می‌توانیم عبارات زیر را بنویسم:

• اگر $$x \ne x_1$$ و $$x \ne x_2$$، آنگاه $$a_t = Ax^n$$.
• اگر $$x = x_1$$ و $$x \ne x_2$$، آنگاه $$a_t = Anx^n$$.
• اگر $$x = x_1 = x_2$$، آنگاه $$a_t = An^2x^n$$.

مثال ۶

رابطه بازگشتی ناهمگن $$F_n = AF_{n–1} + BF_{n-2} + f(n)$$ را با ریشه‌های معادله مشخصه $$x _ 1 =2$$ و $$x _ 2 = 5$$ در نظر بگیرید. جواب‌های آزمایشی (Trial) ممکن مقادیر $$f (n)$$ به صورت زیر هستند:

مثال ۷

رابطه بازگشتی $$F_n = 3F_{n-1} + 10F_{n-2} + 7\cdot 5^n$$ را حل کنید که در آن، $$F_0 = 4$$ و $$F_1 = 3$$.

حل: این رابطه، یک رابطه بازگشتی ناهمگن است که معادله همگن مرتبط با آن، $$F_n=3F_{n-1}+10F_{n-2}$$ بوده و داریم: $$f(n)=7 \cdot 5^n$$.

معادله مشخصه رابطه همگن متناظر به صورت زیر است:‌

$$\large x^2 - 3x -10 = 0$$

یا

$$\large (x - 5)(x + 2) = 0$$

یا

$$\large x_1= 5$$ و $$\large x_2 = -2$$.

بنابراین، $$a_h = a.5^n + b.(-2)^n$$، که در آن، $$a$$ و $$b$$ اعداد ثابتی هستند.

از آنجایی که $$f(n) = 7.5^n$$، یعنی $$c.x^n$$، یک جواب آزمایشی مستدل آن، $$Anx^n$$ است.

$$\large a_t = Anx^n = An5^n$$

بعد از قرار دادن جواب در رابطه بازگشتی، داریم:

$$\large A n 5 ^ n = 3 A ( n – 1 ) 5 ^ { n - 1 } + 1 0 A ( n – 2 ) 5 ^ { n - 2 } + 7 \cdot 5 ^ n$$

با تقسیم هر دو طرف بر $$5^{n-2}$$، خواهیم داشت:

$$\large A n 5 ^ 2 = 3 A ( n - 1 ) 5 + 1 0 A ( n - 2 ) 5 ^ 0 + 7 \cdot 5 ^ 2$$

در نتیجه، $$A=5$$ به دست می‌آید.

بنابراین، $$F_n = An5^n= 5n5^n=n5^{n+1}$$.

جواب رابطه بازگشتی به صورت زیر است:

$$\large F _ n = a _ h + a _ t = a \cdot 5 ^ n + b \cdot ( - 2 ) ^ n + n 5 ^ { n + 1 }$$

با جایگذاری مقادیر $$F_0 = 4$$ و $$F_1 = 3$$ در معادله بالا، مقادیر $$a = -2$$ و $$b = 6$$ به دست می‌آیند. بنابراین، جواب رابطه بازگشتی مورد نظر، برابر است با:

$$\large F _ n = n 5 ^ { n + 1 } + 6 ( - 2 ) ^ n - 2 \cdot 5 ^ n$$