تفریق اعداد اعشاری – به زبان ساده + مثال و تمرین
در آموزشهای پیشین مجله فرادرس، با اعداد اعشاری و همچنین مقایسه و جمع آنها آشنا شدیم. در این آموزش، مطالبی را درباره تفریق اعداد اعشاری بیان میکنیم.

آشنایی با اعداد اعشاری
اعداد اعشاری اعدادی هستند که اعشار دارند و دارای دو قسمت هستند: اولی عدد صحیح (سمت چپ اعشار) و قسمت دوم جزء کسری (راست اعشار). برای مثال، فرض کنید یک بطری شیر ۱۴٫8 هزار تومان (عدد اعشاری) قیمت دارد. در اینجا، عدد صحیح برابر با ۱۴ (سمت چپ اعشار) و قسمت کسری 8 دهم (سمت راست اعشار) است.
«عدد اعشاری» (Decimal Number) عددی است که برای نمایش مقادیری به کار میرود که با اعداد صحیح عادی نمیتوان آنها را بیان کرد. اعشار را با ممیز (یعنی تمایزدهنده) نمایش میدهیم. در دستور خط فارسی، علامت ممیز یک خط کوچک کج است. برای مثال، پنج و هفتدهم را بهصورت ۵٫۷ مینویسیم. دقت کنید که در زبان انگلیسی، ممیز را با نقطه نشان میدهند. مثلاً همان عدد پنج و هفتدهم در زبان انگلیسی به صورت نوشته میشود.
نکته: توجه کنید که علامت کسر (/) با ممیز (٫) تفاوت دارد و اغلب به اشتباه به جای ممیز به کار میرود. همچنین دقت کنید که در اعداد فارسی برای اعشار از نقطه استفاده نکنید. اگر فرض کنیم میخواهیم هشت و سهدهم را بهصورت عددی بنویسیم، خواهیم داشت:
| ۸٫۳ | درست |
| ۸/۳ | نادرست |
| ۸.۳ | نادرست |
| درست |
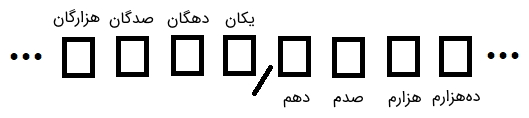
یکی دیگر از مواردی که در رابطه با اعداد اعشاری باید بهخاطر داشته باشیم، ارزش مکانی ارقام و نام آنهاست که در تصویر زیر آن را نشان دادهایم. بنابراین، بهتر است این ارزش مکانی ارقام را به خاطر بسپارید.
تفریق اعداد اعشاری در زندگی واقعی کاربردهای زیادی دارد. برای مثال، اگر بخواهیم تفاوت دمای دو مکان مختلف را محاسبه کنیم، احتمالاً باید روش تفریق اعداد اعشاری را بدانیم. همچنین، دانشمندان از اعداد اعشاری برای حصول و بیان نتایج دقیق در آزمایشهای خود استفاده میکنند. مثالهایی از این دست برای کاربرد تفریق اعداد اعشاری بهوفور یافت میشود. در ادامه، به روش تفریق اعداد اعشاری میپردازیم.

روش تفریق اعداد اعشاری
- ابتدا اعداد اعشاری را که میخواهیم تفریقشان را انجام دهیم، بررسی میکنیم.
- مطمئن میشویم که هر دو اعداد اعشاری دارای تعداد مساوی رقم بعد از نقطه اعشار هستند. اگر نه، 0 اضافی (دارنده ارزش مکانی) را به انتهای عدد اضافه میکنیم تا ارقام بعد از نقطه اعشار برابر شوند.
- هر دو عدد را در قالب تفریق ستونی با ردیف کردن اعشار هر دو عدد، یکی بالای دیگری مینویسیم.
- اعداد اعشاری را از هم کم میکنیم، درست مانند آنچه که برای اعداد صحیح انجام میدهیم. مطمئن میشویم که رقم اعشاری را در پاسخ خود به درستی ردیف کردهایم.
- عدد به دست آمده پاسخ تفریق است.
در ادامه، چند مثال متنوع را برای حالتهای مختلف بیان میکنیم تا با روش انجام تفریق اعداد اعشاری بهخوبی آشنا شوید.
حالت اول: در این حالت دو عدد تعداد ارقام مشابهی دارند و همه ارقام عدد بزرگتر، از ارقام متناظر عدد کوچکتر، بزرگتر هستند.
برای مثال، فرض کنید میخواهیم ۱۱٫۳۴ را از ۴۵٫۸۸ کم کنیم. بدین منظور، باید ابتدا عدد بزرگتر را نوشته، سپس عدد کوچکتر را در زیر آن و با رعایت ارزش مکانی ارقام بنویسیم. کافی است تفریق را برای ارقام هر ستون از راست به چپ انجام دهیم و بنویسیم. ممیز را نیز در ستون خود پایین میآوریم.
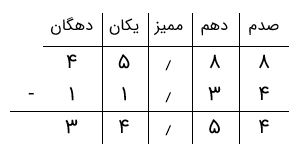
بنابراین، حاصل تفریق ۱۱٫۳۴ - ۴۵٫۸۸ برابر با ۳۴٫۵۴ است.
حالت دوم: گاهی پیش میآید که تعداد ارقام قبل یا بعد از اعشار دو عدد با هم برابر نباشد. در این حالت، کافی است است با افزودن ۰ تعداد ارقام بعد یا قبل از اعشار را با هم برابر کنیم. اما این کار را چگونه انجام دهیم؟
اول اینکه اگر تعداد ارقام قبل از اعشار با هم تفاوت داشت، باید در سمت چپ عددی که ارقام کمتری دارد ۰ اضافه کنیم. قبل از عدد صحیح، هرچه صفر اضافه کنیم، عدد تغییری نمیکند. برای مثال، ۰۱۲٫۲۳ برابر بار ۱۲٫۲۳ است.
دوم اینکه اگر تعداد ارقام بعد از اعشار با هم یکی نبود، به سمت راست عددی که رقم کمتری بعد از اعشار دارد، ۰ اضافه میکنیم. دقت کنید که با این کار ارزش عدد تغییری نمیکند. برای مثال، عدد ۱۲٫۲۳۰ برابر با ۱۲٫۲۳ است.

در اینجا بد نیست نکتهای را متذکر شویم و آن اینکه دقت کنید که وقتی ممیز در عددی به کار میرود، باید آن را با عدد بدون ممیز تمایز دهیم. برای مثال، عدد ۱٫۰۰۰ همان یک است (زیرا صفر بعد از اعشار ارزش به عدد اضافه نمیکند) و ۱۰۰۰ نمایانگر عدد هزار است.
با یک مثال، آنچه را که گفتیم شرح میدهیم. فرض کنید میخواهیم تفریق ۲٫۳ - ۷۳٫۴۸ را انجام دهیم. همانطور که میبینیم، هم تعداد ارقام سمت راست و هم تعداد ارقام سمت چپ دو عدد برابر نیستند. طبق چیزی که گفتیم، به سمت چپ و سمت راست عدد دوم ۰ اضافه میکنیم و سپس برای هر ستون تفریق را انجام میدهیم.
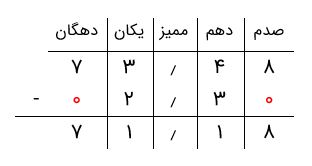
حالت سوم: در برخی موارد، وقتی رقمهای یک ستون را از هم کم میکنیم، رقم بالایی را رقم پایینی ستون کوچکتر است. در این موارد از «رقم قرضی» استفاده میکنیم. با یک مثال روند این کار را توضیح میدهیم.
فرض کنید میخواهیم عدد اعشاری ۲٫۳۱ را از ۸۹٫۶ کم کنیم. بدین منظور، ابتدا تعداد ارقام سمت راست و سمت چپ اعشار را با افزودن ۰ برابر میکنیم. تصویر زیر این موضوع را بهخوبی نشان میدهد.
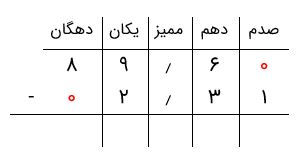
اکنون باید تفریق ارقام هر ستون را با شروع از سمت راست انجام دهیم. در ستون اول باید ۱ را از ۰ کم کنیم. میبینیم که ۱ از صفر کوچکتر است.
در این حالت باید چه کنیم؟ در این موارد باید از ستون سمت چپ ستون موجود قرض بگیریم. بنابراین، در اینجا باید به ستون دهمها برویم و یک رقم قرض بگیریم. بنابراین، از رقم ۶ یکی کم میکنیم و آن را به ستون صدمها میآوریم. در اینجا یک نکته مهم وجود دارد. ما یک واحد از ستون دهمها کم کردهایم، اما در ازای آن باید ۱۰ واحد به ستون صدمها اضافه کنیم، زیرا ارزش ارقام ستون سمت چپ ۱۰ برابر ارزش ارقام ستون سمت راست است. در واقع، هر واحد از دهمها برابر با ۱۰ واحد از صدمهاست. بنابراین، تصویر زیر را خواهیم داشت.
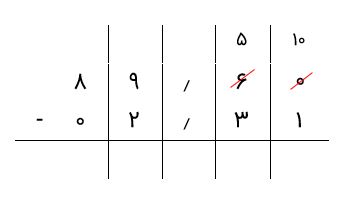
در واقع، اگر بخواهیم جزئیات تصویر بالا را نشان دهیم، بهصورت زیر خواهد بود.
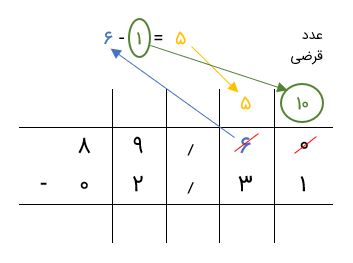
بنابراین، تفریق زیر را برای هر ستون انجام میدهیم.
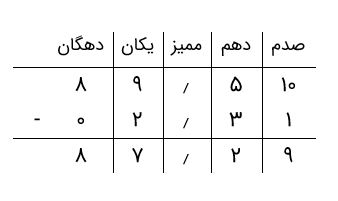
بنابراین، حاصل تفریق برابر با ۸۷٫۲۹ است.
دقت کنید که تفریق اعداد اعشاری چیزی خارج از این سه حالت و یا ترکیب آنها نخواهد بود. بنابراین، با رعایت قواعد سادهای که گفتیم، بهراحتی میتوانید تفریق اعداد اعشاری را انجام دهید.
تفریق اعداد اعشاری با شکل
برای تفریق اعداد اعشاری با کمک شکل، کافی است ابتدا واحدهای مناسب انتخاب کرده و شکل مربوط به عدد بزرگتر را رسم کنیم. سپس بهاندازه شکل دوم از از شکل اول خط بزنیم. آنچه باقی میماند، حاصل تفریق است. با یک مثال این موضوع را شرح میدهیم.
فرض کنید میخواهیم تفریق ۲٫۱۵ - ۴٫۳۷ را انجام دهیم. بدین منظور، ابتدا عدد بزرگتر، یعنی ۴٫۳۷، را با شکل مشخص میکنیم. بنابراین، ۴ واحد کامل، ۳ واحد دهم و ۷ واحد صدم خواهیم داشت.
شکل زیر این عدد را نشان میدهد.

اکنون باید عدد ۲٫۱۵ را از آن کم کنیم. بدین منظور، ۲ واحد کامل و ۱ یکدهم و ۵ یکصدم را حذف میکنیم.
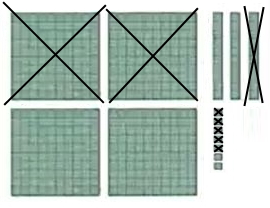
اکنون، شکلهایی را که باقی مانده است، میشماریم. میبینیم که ۲ واحد کامل، ۲ واحد یکدهم و ۲ واحد یکصدم باقی مانده است. بنابراین، جواب ۲٫۲۲ خواهد بود.
تفریق اعداد اعشاری روی محور
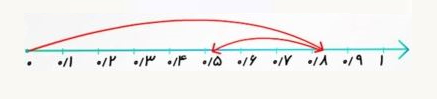
برای تفریق اعداد اعشاری روی محور، ابتدا با یک کمان عدد نخست را مشخص میکنیم. سپس از انتهای کمان اول کمان مربوط به عدد دوم را رسم میکنیم، با این تفاوت که این بار در جهت مخالف عدد نخست. از ابتدای کمان اول تا انتهای کمان دوم نشاندهنده حاصل تفریق است.
برای مثال، فرض کنید میخواهیم عدد ۰٫۳ را از ۰٫۸ کم کنیم. ابتدا عدد ۰٫۸ را روی محور مشخص میکنیم. برای این کار، از صفر شروع کرده و کمانی بهطول ۰٫۸ رسم میکنیم. از انتهای کمان اول، کمانی به طول سه واحدِ یکدهم رسم میکنیم که نشاندهنده عدد اعشاری ۰٫۳ است. جهت این کمان به چپ است. میبینیم که انتهای این کمان روی عدد ۰٫۵ قرار دارد. بنابراین، جواب تفریق دو عدد برابر با ۰٫۵ است.
مثالهای تفریق اعداد اعشاری
در این بخش، چند مثال را از تفریق اعداد اعشاری بررسی میکنیم.
مثال اول
عدد 8٫93 را از عدد 13٫94 کم کنید.
جواب: در اینجا، دو اعداد اعشاری مشابه هستند، به این معنی که تعداد ارقام بعد از اعشار آنها برابر است. کافی است با اضافه کردن صفر به قبل از رقم ۸، ارقام اعشار با ارزش مکانی یکسان را زیر هم مینویسیم. و به همان ترتیبی که در مورد اعداد صحیح انجام میدهیم، تفریق را انجام خواهیم داد.
در بخش یکانها، میبینیم که ۸ از ۳ کوچکتر است. پس از ستون سمت چپ، یک واحد را کم میکنیم، و همان یک واحد دهگان را، که برابر با ۱۰ واحد یکان است، به با رقم بخش یکان جمع میکنیم. بنابراین، عدد ستون دهگان به ۰ تبدیل میشود و عدد یکان برابر با ۱۳ = ۱۰ + ۳ خواهد بود.
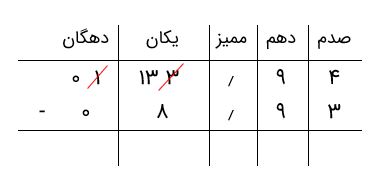
در ادامه، تفریق اعداد ستونها را انجام میدهیم.
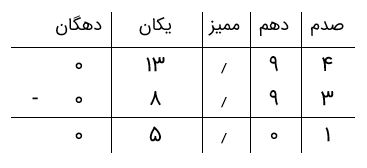
بنابراین، جواب برابر با ۵٫۰۱ خواهد بود.
مثال دوم
در مسابقه دو ۲۰۰ متر، نفر نخست در مدت ۱۹٫۷۵ ثانیه به خط پایان رسیده است و نفر دوم در مدت زمان ۱۹٫۸ ثانیه. اختلاف زمان آنها در رسیدن به خط پایان را محاسبه کنید.

جواب: باید تفریق ۱۹٫۷۵ - ۱۹٫۸ را انجام دهیم. بدین منظور، ابتدا یک ۰ به سمت راست ۱۹٫۸ اضافه میکنیم و تفریق را بهصورت زیر مینویسیم.
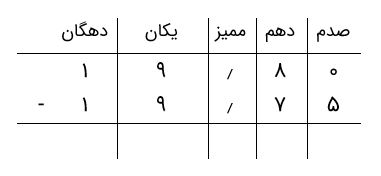
همانطور که میبینیم، ۵ از ۰ کوچکتر است. پس باید از دهمها یک واحد بگیریم و ۱۰ واحد به صدمها اضافه کنیم.
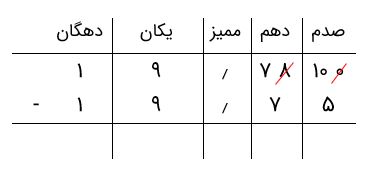
بنابراین، باید تفریق را برای ستونهای زیر انجام دهیم.
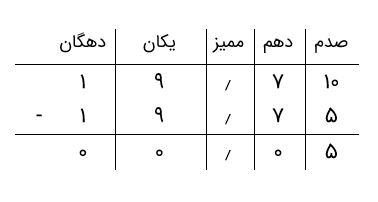
بنابراین، اختلاف زمانی رسیدن دو دونده به خط پایان ۰٫۰۵ است.
مثال سوم
حاصل تفریق 2٫14 + 3٫54 را محاسبه کنید.
جواب: اعداد اعشاری مشابه و دارای تعداد ارقام برابری پس از اعشار هستند. یعنی اگر به اعداد اعشاری داده شده دقت کنیم، میبینیم که آنها از نظر تعداد ارقام مشابه هستند، بنابراین آنها را بهترتیب در زیر هم قرار میدهیم و تفریق را انجام میدهیم. ابتدا صدمها را کم میکنیم: ۰ = ۴ - ۴. سپس، تفریق دهمها برابر با ۴ = ۱ - ۵ است. در ادامه، اعشار را مینویسیم. تفریق یکانها نیز ۲ = ۱ - ۳ است. بنابراین، حاصل تفریقبرابر با ۱٫۴۰ یا همان ۱٫۴ است.
مثال چهارم
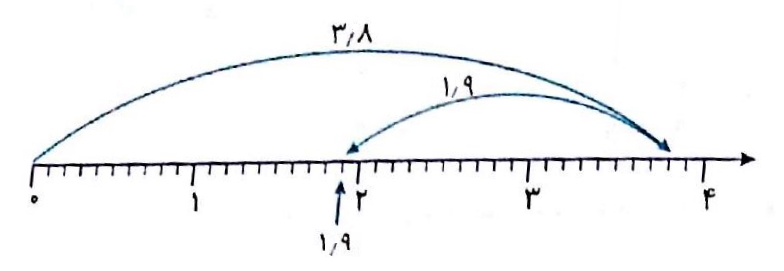
با کمک محور اعداد، حاصل تفریق عدد ۱٫۹ از عدد ۳٫۸ را بهدست آورید.
جواب: بدین منظور، کافی است کمانی بهاندازه ۳ واحد کامل و ۸ واحد یکدهم رسم کنیم. سپس از انتهای این کمان، سک کمان دیگر در جهت مخالف رسم کنیم که اندازه آن ۱٫۹ است. میبینیم که انتهای کمان دوم روی عدد ۱٫۹ میافتد. بنابراین، جواب برابر با ۱٫۹ است.
مثال پنجم
عدد را از عدد ۷٫۷۷۷ کم کنید.
جواب: ابتدا باید عدد مخلوط را به عدد اعشاری تبدیل کنیم. بدین منظور، ابتدا آن را به یک کسر متعارفی تبدیل میکنیم:
مخرج این کسر است و باید آن را به یک عدد مضرب تبدیل کنیم. با ضرب آن در به میرسیم که مضرب است. بنابراین، خواهیم داشت:
اکنون، صورت کسر را مینویسیم، و از راست سه رقم اعشار را جدا میکنیم:
برای آشنایی بیشتر با تبدیل عدد مخلوط به کسر، به آموزش «تبدیل عدد مخلوط به کسر — به زبان ساده + حل تمرین و مثال» مراجعه کنید.
بنابراین، باید تفریق دو عدد اعشاری ۲٫۱۲۵ و ۷٫۷۷۷ را انجام دهیم. بدین منظور، دو عدد را با رعایت ارزش مکانی ارقامشان مینویسیم و تفریق را انجام میدهیم.
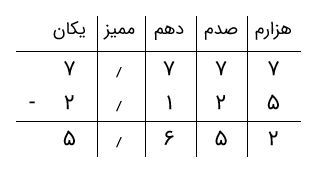
در نتیجه، جواب برابر با ۵٫۶۵۲ خواهد بود.
مثال ششم
عدد را از کم کنید.
جواب: ابتدا باید کسر را به باید ببینیم عدد را در چه عددی ضرب کنیم تا حاصل مضربی از شود. اگر از ماشین حساب کمک بگیریم، با کمی سعی و خطا به عدد میرسیم و خواهیم داشت:
اکنون، عدد صورت، یعنی را مینویسیم، و از راست چهار رقم اعشار را جدا میکنیم:
برای آشنایی بیشتر با تبدیل کسر به اعشار، به آموزش «تبدیل کسر به اعشار — به زبان ساده + حل تمرین و مثال» مراجعه کنید.
بنابراین، باید تفریق دو عدد ۰٫۱۸۷۵ و ۰٫۸۸۸ را انجام دهیم. بدین منظور، دو عدد را زیر هم مینویسیم و از سمت راست شروع میکنیم و ارقام را کم میکنیم. البته ابتدا باید یک صفر به سمت راست ۰٫۸۸۸ اضافه کنیم تا تعداد ارقام پس از اعشار با هم برابر شود.
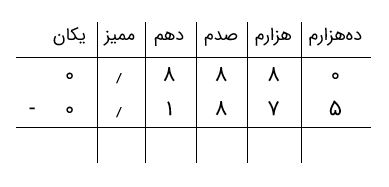
مطابق معمول، از ستون سمت راست، که کمترین ارزش مکانی را دارد، شروع میکنیم. میبینیم که ۰ از ۵ کوچکتر است. بنابراین، باید از ستون هزارمها کمک بگیریم و ۱ واحد از آن ردیف را که برابر ۱۰ واحد از دههزارمها است، به ستون اول منتقل کنیم. در نتیجه، تصویر زیر را خواهیم داشت.
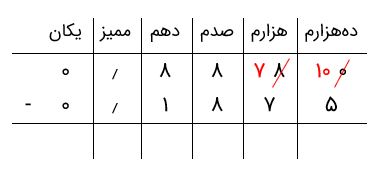
بنابراین، حاصل تفریق بهراحتی محاسبه میشود.
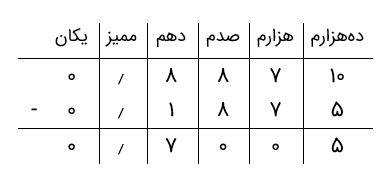
در نتیجه، جواب برابر با ۰٫۷۰۰۵ خواهد بود.

مثال هفتم
حاصل تفریق ۶٫۳۷ از ۱۵٫۶۵۲ را بهدست آورید.
جواب: ابتدا دو عدد را زیر هم مینویسیم (عدد بزرگ در بالا) و سپس برای برابر شدن ارقام قبل و بعد از اعشار، صفر اضافه میکنیم.
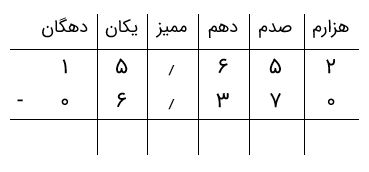
از ستون سمت راست شروع میکنیم و تفریق را انجام میدهیم که حاصل آن ۲ = ۰ - ۲ است. به ستون صدمها میرویم. میبینیم که ۷ از ۵ کوچکتر است. بنابراین، از ستون دهمها یکی کم میکنیم و به ستون صدمها ۱۰ تا اضافه. اکنون رقم تفریق ستون صدمها برابر با ۸ = ۷ - ۱۵ و تفریق مربوط به ستون دهمها ۲ = ۳ - ۵ است. سپس اعشار را قرار میدهیم.
اکنون باید یکانها را کم کنیم. میبینیم که ۶ از ۵ کوچکتر است. بنابراین، از دهگانها کمک میگیریم و یکی را از آنها کم میکنیم و معادلش، یعنی ۱۰ تا یکی را به ستون یکانها اضافه میکنیم. اکنون باید در ستون یکانها ۶ را از ۱۵ کم کنیم که حاصلش میشود عدد ۹. در ستون دهگانها نیز ۰ از ۰ کم میشود و حاصلش همان ۰ است.
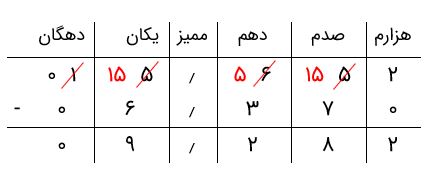
پس، جواب برابر با ۹٫۲۸۲ خواهد بود.
جمعبندی
در این آموزش، ضمن معرفی اعداد اعشاری با روشهای تفریق آنها آشنا شدیم و بهصورت گام به گام آنها را شرح دادیم. در پایان نیز به حل مثالهایی از تفریق اعداد اعشاری پرداختیم.
آزمون تفریق عداد اعشاری
۱. کدام بخش از عدد ۷٫۲۴، جزء صحیح آن را نشان میدهد؟
عدد ۴ که آخرین رقم سمت راست است.
عدد ۷ که در سمت چپ ممیز قرار دارد.
کل عبارت ۷٫۲۴ به طور کامل جزء صحیح است.
عدد ۲ که در سمت راست ممیز دیده میشود.
در عدد ۷٫۲۴، بخش «عدد ۷ که در سمت چپ ممیز قرار دارد» نمایانگر جزء صحیح عدد است، زیرا طبق توضیح ساختار اعداد اعشاری، قسمت چپ ممیز همیشه بخش صحیح را نشان میدهد.
۲. در نگارش اعداد اعشاری، ممیز اعشاری و علامت کسر / چه تفاوتی با هم دارند؟
ممیز اعشاری عدد را به دو بخش صحیح و اعشاری جدا میکند، اما علامت کسر برای نشان دادن نسبت دو عدد است.
علامت کسر / تنها در زبان انگلیسی و ممیز اعشاری در فارسی به کار میرود.
ممیز اعشاری و علامت کسر / فقط جایگاه متفاوت دارند اما معنی یکسانی ارائه میدهند.
هر دو فقط برای نمایش اعداد اعشاری به کار میروند و تفاوتی ندارند.
استفاده از «ممیز اعشاری» عدد را به دو بخش صحیح و اعشاری تقسیم میکند و مخصوص نمایش اعداد اعشاری است، یعنی قسمت سمت چپ مربوط به عدد صحیح و سمت راست مربوط به بخش اعشاری است. «علامت کسر /» اما برای نمایش نسبت یا تقسیم دو عدد به کار میرود و معنای اعشاری مستقیمی ندارد. به عنوان مثال ۳/۴ به معنی سه چهارم است، نه یک عدد اعشاری.
۳. ارزش مکانی رقم ۵ در عدد ۳۲٫۵۷ چیست و این ارزش در تفریق اعداد اعشاری چه نقشی دارد؟
عدد ۵ بخشی از قسمت صحیح است و مقدار آن پنج واحد حساب میشود.
عدد ۵ در جایگاه صدم بوده و ارزش آن پنج صدم است که در جمع و تفریق تاثیر کمی دارد.
عدد ۵ در جایگاه دهم بوده و ارزش آن پنج دهم است که در محاسبات اعشاری اهمیت زیادی دارد.
عدد ۵ رقم بعد از ممیز نبوده و در تفریق اثری ندارد.
عدد ۵ در عدد ۳۲٫۵۷ بلافاصله بعد از ممیز قرار گرفته که نشاندهنده جایگاه دهم است و مقدار آن پنج دهم محسوب میشود. این ارزش مکانی تعیین میکند که در عملیاتهایی مانند تفریق اعداد اعشاری، دقیقا باید رقم دهم را با رقم مشابه خودش مقایسه و محاسبه کرد.
۴. در زمان تفریق اعداد اعشاری، اگر تعداد رقم اعشار یکی از دو عدد کمتر باشد، کدام کار باعث اجرای درست تفریق میشود؟
ضرب عدد اعشاری کوتاهتر در ده
اضافه کردن صفر به انتهای عدد اعشاری کوتاهتر
کاهش عدد بزرگتر به اندازه رقم اعشار کمتر
قراردادن ممیز در ابتدای هر دو عدد
اگر در تفریق اعشاری تعداد رقم اعشار دو عدد برابر نباشد، با «اضافه کردن صفر به انتهای عدد اعشاری کوتاهتر» میتوان تعداد ارقام اعشاری هر دو عدد را یکسان کرد تا تفریق به درستی انجام شود.
۵. در تفریق ستونی اعداد اعشاری، اگر هنگام عمل رقم بالایی از رقم پایینی کوچکتر بود، کدام راهکار طبق آموزش برای ادامه صحیح محسوب میشود؟
کافی است رقم بالایی را بدون تغییر بنویسیم و به رقم بعدی برویم.
صفر به انتهای عدد کوچکتر اضافه کنیم تا رقمها برابر شوند.
از رقم سمت چپ عدد بزرگتر قرض بگیریم و عمل تفریق را ادامه دهیم.
باید اعداد اعشاری را با یکدیگر مقایسه کرده و عملیات را متوقف کرد.
وقتی رقم بالایی کوچکتر از رقم پایینی باشد، باید از رقم سمت چپ عدد بزرگتر قرض بگیریم تا بتوان تفریق را انجام داد. این روش برای حل بسیاری از مسئلههای تفریق اعشاری ضروری است، چون در اکثر اعداد، عدم تساوی بین ارقام باعث همین نیاز میشود.













بسیار عااالی. تشکر