ترانهاده ماتریس — به زبان ساده

در راستای طرح مباحث مرتبط با ماتریس‌ها، پیش‌تر در بلاگ فرادرس مفاهیم بنیادین ماتریس‌ها، معکوس ماتریس،‌ دترمینان ماتریس و نحوه بدست آوردن معکوس ماتریس ۳×۳ را توضیح دادیم. در این مطلب قصد داریم تا ماتریس ترانهاده یا ترانهاده ماتریس (Matrix Transpose) را که در بدست آوردن دیگر ماتریس‌ها نیز کاربرد دارد، توضیح دهیم.

مقدمه

ترانهاده، ابزاری است که در بدست آوردن ماتریس معکوس و بسیاری دیگر از مفاهیم جبر خطی کاربرد دارد.

فیلم آموزش ماتریس ها و جبر خطی – حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

این ماتریس به دیگر ویژگی‌های یک ماتریس‌ هم‌چون مربعی بودن، معکوس‌پذیر بودن و متقارن بودن آن وابسته است. یکی از کاربرد‌های مهم این مفهوم در تانسور‌ها و در آنالیز برداری است. البته از این مفهوم برای ضرب دو بردار نیز استفاده می‌شود.

بدست آوردن ترانهاده ماتریس

برای بدست آوردن ماتریس ترانهاده، می‌توان به روش‌های گوناگونی عمل کرد. توجه داشته باشید که هر ماتریسی با هر مرتبه‌ و ویژگی را می‌توان به‌صورت ترانهاده بیان کرد.

فیلم آموزش ساختارهای جبری، گراف ها و ماتریس ها در فرادرس

کلیک کنید

به‌منظور بدست آوردن ترانهاده به‌ترتیب زیر عمل کنید.

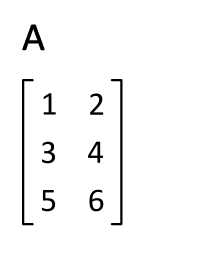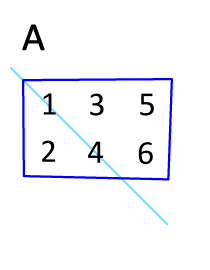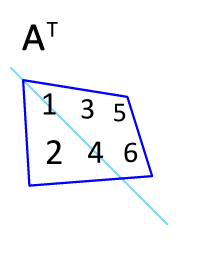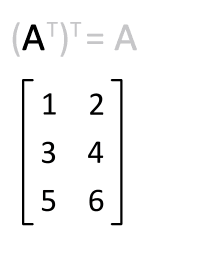
در ابتدا ماتریس A را به‌صورت زیر در نظر بگیرید.

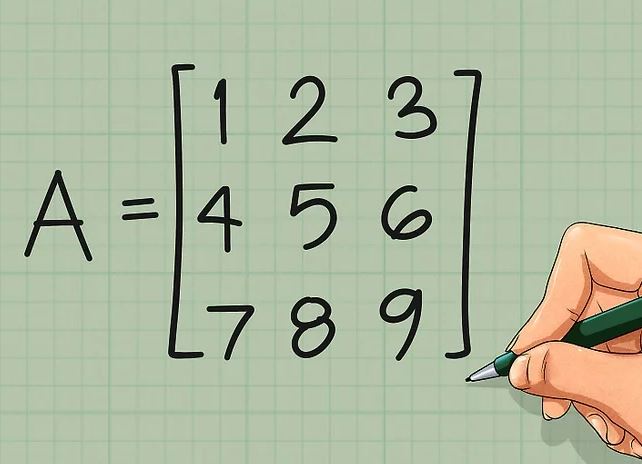
همان‌طور که می‌بینید به‌منظور راحتی کار ماتریس A به‌صورت مربعی در نظر گرفته شده.

قدم اول

مطابق با تصویر زیر، سطر اول ماتریس A را در ستون اول قرار دهید.

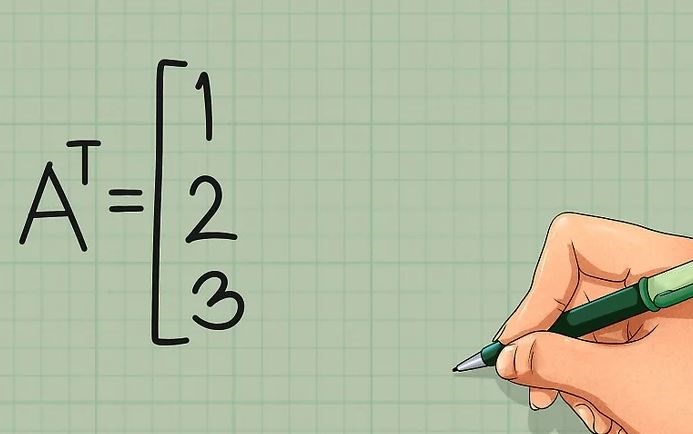
قدم دوم

همان‌طور که در شکل زیر نشان داده شده، قدم اول را برای دیگر سطر‌ها نیز انجام دهید. نهایتا ماتریس A^T، مطابق با تصویر زیر بدست می‌آید.

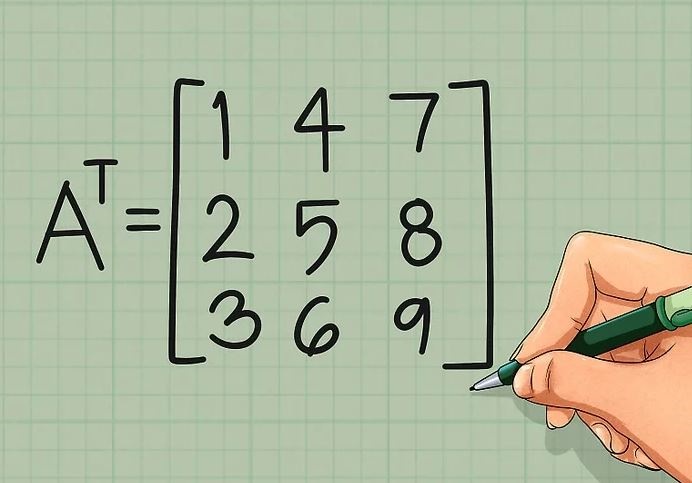
همان‌طور که در تصویر بالا نیز نشان داده شده، سطر دوم ماتریس A در ستون دوم ماتریس ترانهاده (A^T)، نوشته شده است. به همین صورت سطر سوم در ستون سوم و الی آخر نوشته می‌شود.

با توجه به توضیحات بالا اعدادی که روی قطر ماتریس قرار می‌گیرند، ثابت می‌ماند.

قدم سوم

همان‌طور که دیدید بدست آوردن ماتریس ترانهاده بسیار آسان بوده و حتی می‌توان به صورت ذهنی آن را تصور کرد. اما در بسیاری از کاربرد‌ها، بایستی بتوانید شکل ریاضیاتی آن را نیز بیان کنید.

فیلم آموزش اکسل – محاسبات ریاضی و ماتریسی با Microsoft Excel 2016 در فرادرس

کلیک کنید

در مورد ماتریس ترانهاده عبارات زیر را به خاطر بسپارید:

• اگر ماتریس B به صورت m×n باشد، آن‌گاه ماتریس B^T، به شکل n×m در خواهد آمد.
• مولفه b_ij در ماتریس B برابر با مولفه b_ji در ماتریس B^T است.

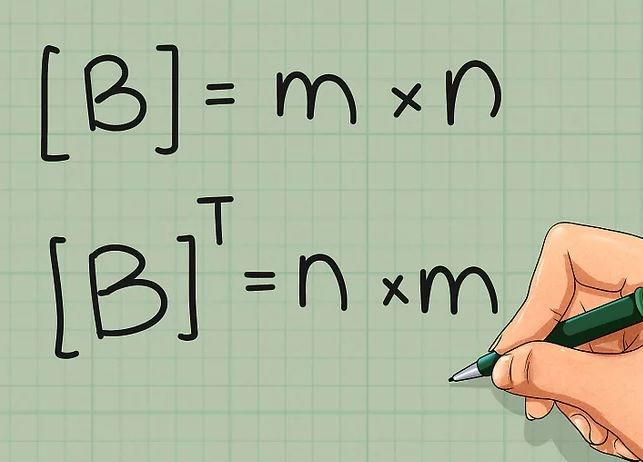
نکات

در ماتریس ترانهاده نکات مهمی نهفته است که بایستی آن‌ها را فرا بگیرید.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

M^T)^T=M)

برای هر ماتریس دلخواهی هم‌چون M، رابطه M^T)^T=M) برقرار است. این رابطه می‌گوید ترانهاده‌ی ترانهاده یک ماتریس برابر با خود ماتریس می‌شود.

قرینه ماتریس حول قطر اصلی

ممکن است زمان زیادی برای حل یک مسئله ریاضی نداشته باشید؛ بنابراین در چنین شرایطی به‌منظور بدست آوردن ترنهاده ماتریس می‌توانید آن را حول قطر اصلیش قرینه کنید. در حقیقت مولفه‌های روی قطر اصلی را نگه داشته و بقیه اجزا را حول آن دوران دهید. برای نمونه در انیمیشن زیر نحوه بدست آمدن ماتریس ترانهاده نشان داده شده. همان‌طور که می‌بینید ماتریس A نسبت به محور اصلیش معکوس شده است.

این روش خصوصا در مواردی که با ماتریس‌های مربعی مواجه هستید، می‌تواند بسیار مفید باشد.

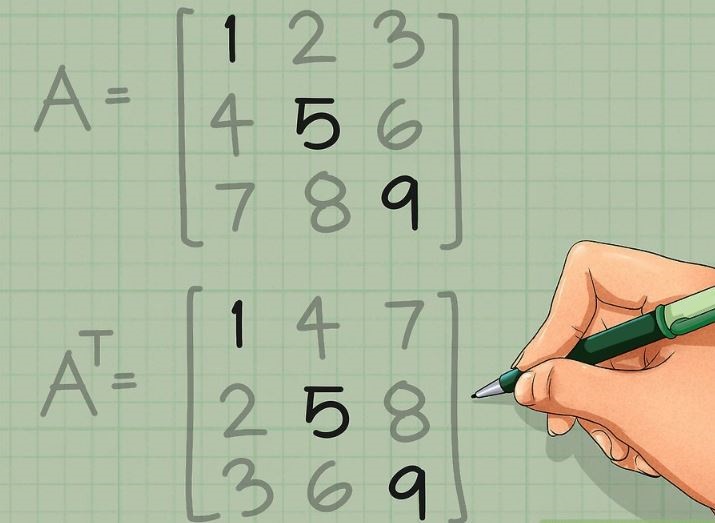
همان‌طور که در شکل فوق نیز می‌بینید مولفه‌های روی قطر اصلی ثابت نگه داشته شده‌اند.

ماتریس متقارن

ماتریس متقارن، ماتریسی است که مولفه‌های آن نسبت به قطر اصلیش متقارن باشند. بدیهی است که ترانهاده چنین ماتریسی خودش می‌شود. بنابراین اگر A ماتریسی متقارن باشد، رابطه زیر را می‌توان برای آن نوشت.

$$\large A^T=A$$

ترانهاد مزدوج

عدد مختلط، عددی است که از دو بخشِ حقیقی و موهومی تشکیل شده و می‌توان آن را معادل با یک بردار فرض کرد. البته در صورت علاقه‌مندی به مبحث اعداد مختلط می‌توانید به این لینک مراجعه فرمایید.

فیلم آموزش جبر خطی – مرور و حل مساله در فرادرس

کلیک کنید

اگر حتی یکی از مولفه‌های ماتریس،‌ عددی مختلط باشد،‌ آن ماتریس مختلط فرض می‌شود. برای نمونه ماتریس زیر نمونه‌ای از یک ماتریس مختلط است.

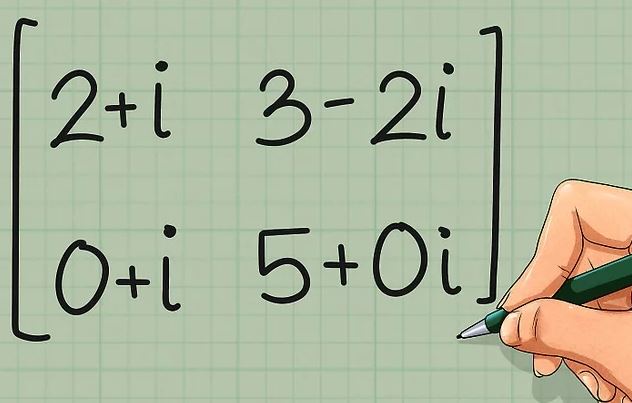
برای چنین ماتریس‌هایی می‌توان ماتریسی تحت عنوان «ترانهاد مزدوج» (Conjugate Transpose) را تعریف کرد. به‌منظور یافتن چنین ماتریس‌هایی در ابتدا بایستی بخش موهومی هر درایه را قرینه کرده، سپس ترانهاده آن را نوشت. برای نمونه ماتریس فوق را در نظر بگیرید. به‌منظور نوشتن ترانهاده آن در ابتدا بخش موهومی هر مولفه را قرینه کنید (ماتریس زیر).

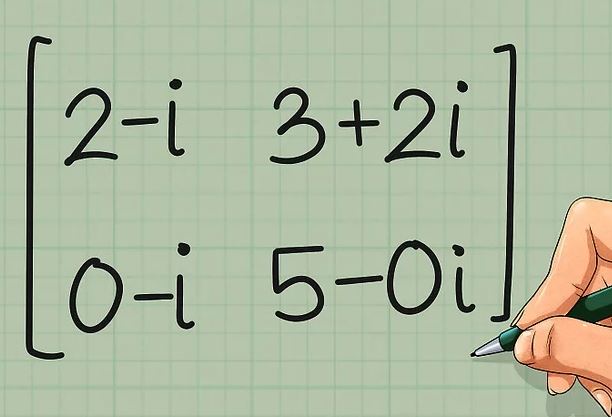
در مرحله بعد ترانهاده‌ی ماتریس قرینه شده -در بالا- را مطابق با ماتریس زیر بنویسید.

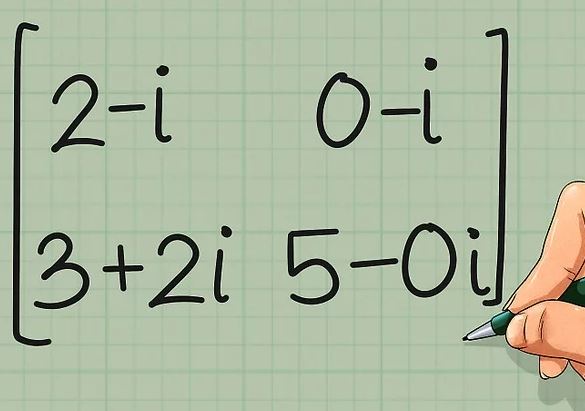
معمولا ماتریس ترانهاده مزدوج را با نماد H نمایش می‌دهند. بنابراین در مورد مثال فوق می‌توان نوشت:

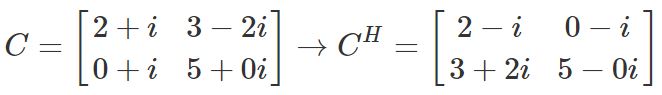
ویژگی‌های ترانهاده

ماتریس ترانهاده دارای ویژگی‌هایی است که در اثبات قضایای ریاضی و فیزیک بسیار از آن‌ها استفاده می‌شود.

فیلم آموزش روش های عددی در جبر خطی در فرادرس

کلیک کنید

مهم‌ترین ویژگی‌های یک ماتریس ترانهاده به شرح زیر هستند:

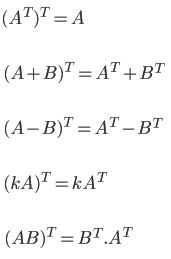
ویژگی آخر بیان شده ($$( A B ) ^ T = B ^ T A ^ T$$)، نکته جالبی را در خود دارد. در حقیقت اگر در این رابطه به‌جای B، ماتریسِ A^T قرار گیرد $$( ( A A ^ T ) ^ T )$$، رابطه $$( A A ^ T ) ^ T = ( A ^ T ) ^ T A ^ T = A A ^ T$$ بدست می‌آید. بنابراین ترانهاده ماتریسِ $$( A A ^ T )$$ برابر با خودش است. در حقیقت ماتریس $$A A ^ T$$ متقارن است. از این نکته که حاصل ضرب یک ماتریس در ترانهاده‌اش، ماتریسی متقارن بوده، بسیار استفاده می‌شود.