فرادرستجزیه عبارت های جبری — آموزش به زبان ساده و با مثال
در آموزش‌های قبلی مجله فرادرس، با اتحاد و تجزیه آشنا شدیم. در این آموزش می‌خواهیم به طور خاص روش‌های تجزیه عبارت های جبری را بررسی و مثال‌هایی را در این زمینه حل کنیم.
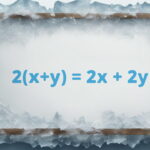
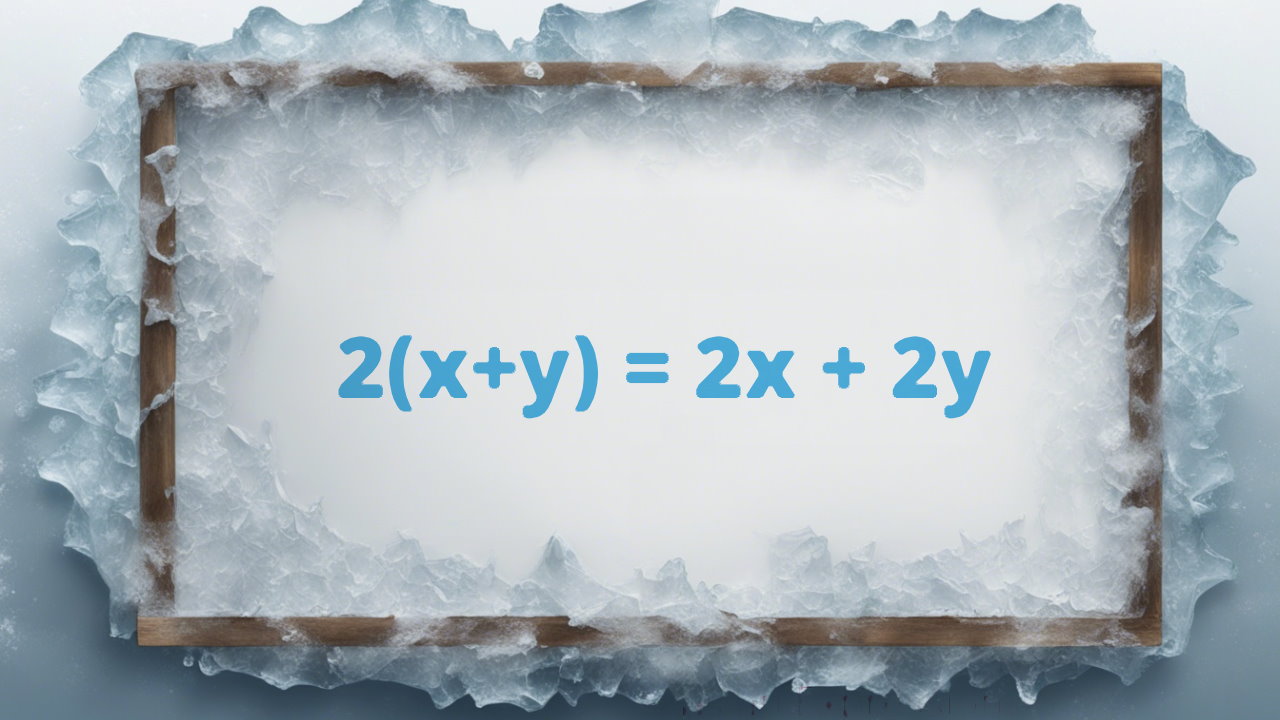
تجزیه عبارت های جبری چیست؟
قبل از پرداختن به روش‌ها و مثال‌های تجزیه عبارت های جبری یا همان چندجمله‌ای‌ها، باید ابتدا دریابیم که تجزیه عبارت های جبری دقیقاً چیست و در ریاضیات چه تعبیری دارد. همان‌طور که می‌دانیم، عبارت جبری یا همان چندجمله‌ای از ترکیب اعداد، متغیرها و عملیات ریاضی (جمع و تفریق و ضرب و تقسیم) ساخته می‌شود.
وقتی یک عبارت جبری یا چندجمله‌ای درجه $$n$$ داریم و می‌خواهیم آن را تجزیه کنیم، منظورمان این است که عبارت جبری را تا حد امکان به گونه‌ای ساده کنیم که بتوانیم آن را به صورت ضرب چند عبارت با درجه کمتر از $$n$$ بنویسیم.
ابزارهای تجزیه عبارت های جبری
در تجزیه عبارت های جبری یا همان چندجمله‌ای‌ها معمولاً از اتحادها و همچنین، فاکتورگیری کمک می‌گیریم.
فاکتورگیری
یکی از ابزارهای ساده و بسیار کاربردی تجزیه عبارت های جبری این است که از عامل‌های مشترک فاکتور بگیریم. این کار را با بزرگ‌ترین مقسوم‌علیه مشترک یا ب.م.م. انجام می‌دهیم. برای مثال، فرض کنید
برای مثال، عبارت زیر را در نظر بگیرید:
$$ \large 3 x y ^ 2 z + 6 x y - 12 x^2 y ^ 2 $$
می‌بینیم که در بین این سه جمله، جمله $$ 3 x y $$ مشترک است و می‌توانیم از آن فاکتور بگیریم. به‌عبارت دیگر، برای سه جمله، می‌توان نوشت:
$$ \large \begin {align}
3 x y ^ 2 z & = 3 x y (y z )\\
6 x y & = 3 x y (2) \\
- 12 x^2 y ^ 2 & = 3 x y (-4x y)
\end {align} $$
بنابراین، می‌توان نوشت:
$$ \large \begin {align}
3 x y ^ 2 z + 6 x y - 12 x^2 y ^ 2 & = 3 x y (yz + 2 -4x y)
\end {align} $$
دسته‌بندی
گاهی اوقات که عبارت جبری بیش از سه جمله باشد، می‌توانیم جای جملات را به‌گونه‌ای تغییر دهیم که بتوانیم از اتحادها یا فاکتورگیری استفاده کنیم.
برای مثال، فرض کنید عبارت زیر را داریم:
$$ \large y ^ 3 + x ^ 2 +x y ^ 2 + x y $$
با کمی تغییر در جای جملات، عبارت را این‌گونه می‌نویسیم:
$$ \large ( y ^ 3 +x y ^ 2 )+ (x ^ 2 + x y) $$
همان‌طور که می‌بینیم، در پرانتز اول $$y ^ 2 $$ و در پرانتز دوم $$ x $$ بین جملات مشترک است. بنابراین، می‌توان نوشت:
$$ \large y ^ 2 ( y +x )+ x (x + y) $$
می‌بینیم که عبارت $$ (x+y)$$ مشترک است و می‌توانیم از آن فاکتور بگیریم:
$$ \large ( x + y ) ( y ^2+x )$$
می‌بینیم که عبارت با استفاده از دسته‌بندی و سپس فاکتورگیری تجزیه می‌شود.
شکستن جملات
گاهی می‌توانیم جملات یک عبارت را با توجه به سایر جملات بشکنیم، سپس آن‌ها را دسته‌بندی کنیم و در نهایت عبارت را تجزیه کنیم.
برای مثال، عبارت زیر را در نظر بگیرید:
$$ \large 2 x ^ 2 + 3 x + 1 $$
جمله $$ 2 x ^ 2 $$ را به‌صورت $$ x ^ 2 + x ^ 2 $$ و جمله $$ 3x $$ را به‌صورت $$ 2 x + x $$ می‌شکنیم و می‌نویسیم:
$$ \large x ^ 2 + x ^ 2 + 2 x + x + 1 $$
اکنون جملات را این‌گونه دسته‌بندی می‌کنیم:
$$ \large ( x ^ 2 + 2 x + 1 ) +( x ^ 2 + x ) $$
پرانتز سمت چپ یک سمت اتحاد مربع دوجمله‌ای را نشان می‌دهد (در بخش بعدی با آن آشنا می‌شویم)، در پرانتز دوم نیز می‌توانیم از $$ x $$ فاکتور بگیریم. بنابراین، می‌توان نوشت:
$$ \large ( x +1 )^ 2 + x ( x + 1 ) $$
اکنون، می‌بینیم که $$(x + 1 ) $$ عامل مشترک است و می‌توانیم از آن فاکتور بگیریم:
$$ \large ( x + 1 ) [ ( x +1 ) + x] = ( x + 1 ) ( 2 x + 1 ) $$
می‌بینیم که عبارت به‌خوبی تجزیه شده است.
استفاده از اتحادها
گاهی شکل ظاهری چندجمله‌ای دقیقاً مانند اتحادهای معروف است. در این صورت به راحتی می‌توانیم از اتحادها استفاده کرده و تجزیه عبارت های جبری را به‌خوبی انجام دهیم. البته گاهی باید از تکنیک‌های ریاضی استفاده کنیم، تکنیک‌هایی مانند کم و زیاد کردن جملات جدید، شکستن جملات موجود و... . برای تجزیه آسان عبارت های جبری می‌توانیم از فاکتورگیری نیز استفاده کنیم. در مثال‌هایی که در ادامه بیان می‌کنیم، به این موارد اشاره خواهیم کرد.
مهم‌ترین اتحادهایی که از آن‌ها در تجزیه عبارت های جبری استفاده می‌شود، به عبارتند از:
- اتحاد مربع دوجمله‌ای:
$$ \large \boxed { \begin {align}
a ^ 2 + 2 a b + b ^ 2 & = (a + b ) ( a + b )= ( a + b ) ^ 2 \\
a ^ 2 - 2 a b + b ^ 2 & = (a - b ) ( a - b )= ( a - b ) ^ 2
\end {align} } $$
- اتحاد مربع سه‌جمله‌ای:
$$ \large \boxed { \begin {align}
a ^ 2 + b ^ 2 + c ^ 2 + 2 a b + 2ac + 2 b c & = ( a + b + c ) ^ 2
\end {align} } $$
- اتحاد مکعب دوجمله‌ای:
$$ \large \boxed { \begin {align}
a ^ 3 + 3 a ^ 2 b + 3 a b ^ 2 + b ^ 3 & = ( a + b ) ^ 3 \\
a ^ 3 - 3 a ^ 2 b + 3 a b ^ 2 - b ^ 3 & = ( a - b ) ^ 3
\end {align} } $$
$$ \large \boxed { \begin {align}
a ^ 3 + b ^ 3 & = ( a + b ) (a ^ 2 - a b + b ^ 2 ) \\
a ^ 3 - b ^ 3 & = ( a - b ) (a ^ 2 + a b + b ^ 2 )
\end {align} } $$
- اتحاد مزدوج:
$$ \large \boxed { \begin {align}
a ^ 2 - b ^ 2 = ( a + b ) (a - b )
\end {align} } $$
- اتحاد جمله مشترک:
$$ \large \boxed { \begin {align}
x ^ 2 + ( a +b ) x + ab = ( x + a ) ( x + b)
\end {align} } $$
- اتحاد بسط دوجمله‌ای نیوتن:
$$ \large \boxed { \begin {align}
\begin {array} {l}
a ^ { n } + \left ( \begin {array} { l }
n \\ 1
\end {array} \right ) a ^ { n - 1 } b + \left ( \begin {array} { l }
n \\ 2
\end {array} \right ) a ^ { n - 2 } b ^ { 2 } + \ldots + \left ( \begin {array} { l }
n \\ n
\end {array} \right ) b ^ { n } = ( a + b ) ^ { n } \\
a ^ { n } - \left ( \begin {array} { l }
n \\ 1
\end {array} \right ) a ^ { n - 1 } b + \left ( \begin {array} { l }
n \\ 2
\end {array} \right ) a ^ { n - 2 } b ^ { 2 } - \ldots + ( - 1 ) ^ { n } b ^ { n } = ( a - b ) ^ { n }
\end {array}
\end {align} } $$
- اتحاد لاگرانژ:
$$ \large \boxed { \begin {align}
( a x + b y ) ^ 2 + ( a y - b x ) ^ 2 = (a ^ 2 + b ^ 2 ) (x ^ 2 + y ^ 2 )
\end {align} } $$
- اتحاد اویلر:
$$ \large \boxed { \begin {align}
a ^ 3 + b ^ 3 + c ^ 3 - 3 a b c = ( a + b + c ) (a ^ 2 + b ^ 2 + c ^ 2 - a b - a c - b c )
\end {align} } $$
برای تجزیه عبارتهای جبری، ابتدا عبارت را به دقت بررسی کنید و به دنبال اشتراک در جمله‌ها باشید تا در صورت امکان از فاکتورگیری استفاده کنید. مثلاً در عبارت $$xy + xy^2 - 8xy+x^2y^2 $$ اگر کمی دقت کنیم، می‌بینیم که $$xy$$ در همه جملات مشابه است و می‌توان عبارت را به صورت $$ xy ( 1 + y-8+xy)$$ نوشت.
نکته دیگر که بسیار به تجزیه عبارت های جبری کمک می‌کند، استفاده از اتحادها است. به همین دلیل، بهتر است همه اتحادهای مهم را به خاطر بسپارید و عبارت جبری را از جنبه اتحادها بررسی کنید.
در ادامه، مثال‌های مختلفی را برای تجزیه عبارت های جبری با استفاده از روش‌های مختلف بیان می‌کنیم.
مثال های تجزیه عبارت های جبری
در این بخش، چند مثال از تجزیه عبارت های جبری را حل می‌کنیم.
مثال اول تجزیه عبارت های جبری
کدام‌یک از عبارتهای زیر تجزیه شده‌اند؟
(الف) $$ x^2-4x+4 = (x-2)^2$$
(ب) $$a ^ 4+4 = (a^4+2)(a^2+2)-(2a)(2a)$$
(ج) $$ a ^ 3 + b ^ 3 = ( a + b ) (a ^ 2 – a b + b ^ 2 ) $$
(د) $$20y^2 - 10y =10 y (2y - 1 )$$
حل: تساوی (الف) تجزیه عبارت جبری را نشان می‌دهد. چون همان‌طور که مشخص است، $$ x^2-4x+4 = (x-2)^2=(x-2)(x-2)$$ نشان می‌دهد که طبق تعریفی که بیان کردیم، چندجمله‌ای درجه ۲ به صورت حاصل‌ضرب دو چندجمله‌ای درجه ۱ نوشته شده است. سمت راست تساوی (ب) تجزیه عبارت سمت چپ نیست، چون به صورت ضرب چندجمله‌ای‌ها نیست. در اتحاد (ج) تجزیه سمت چپ در سمت راست قرار دارد. در تساوی (د) نیز تجزیه انجام شده و سمت راست به صورت ضرب دو چندجمله‌ای نوشته شده که درجه‌شان از چندجمله‌ای سمت چپ کمتر است.
مثال دوم تجزیه عبارت های جبری
عبارت $$ x ^ 6 - y ^ 6 $$ را تجزیه کنید.
حل: این عبارت را می‌توان به دو صورت زیر نوشت:
$$ \large \begin{align*} x ^ 6 - y ^ 6 & = (x^2)^ 3 - (y^2)^3 \\
x ^ 6 - y ^ 6 &= (x ^ 3 )^ 2 - (y ^ 3 ) ^ 2 \end {align*} $$
با هر دو تساوی می‌توان مسئله را حل کرد. ابتدا فرض کنید اولی، یعنی تفاضل مکعب دو جمله $$x^2$$ و $$ y ^ 2 $$ را در نظر می‌گیرم. بنابراین، خواهیم داشت:
$$ \large \begin {aligned}
x ^ { 6 } - y ^ { 6 } & = \left ( x ^ { 2 } \right ) ^ { 3 } - \left ( y ^ { 2 } \right ) ^ { 3 } \\
& = \left ( x ^ 2 - y ^ 2 \right ) \left ((x ^ 2 )^ 2 + (x^2 ) (y ^ 2 ) + ( y ^ 2 ) ^ 2 \right ) \\ & = (x-y)(x+y) (x ^ 4 + x^2 y ^2+ y ^ 4 ) \\ & = ( x - y ) ( x + y) (x^ 4 + 2 x ^ 2 y ^ 2 - x ^ 2 y ^ 2 + y ^ 4 )\\ & = ( x - y ) ( x + y) [ ( x ^ 4 + 2 x ^2 y ^ 2 + y ^ 4 )- x ^ 2 y ^ 2 ] \\
& = ( x - y ) ( x + y) [ ( x ^2+ y ^ 2 ) ^ 2- x ^ 2 y ^ 2 ] \\
& = ( x - y ) ( x + y) [(x ^ 2 + y ^ 2 - xy )(x ^ 2 + y ^ 2 + xy)] \\ & =
( x - y ) ( x + y) (x ^ 2 - xy + y ^ 2)(x ^ 2 + xy + y ^ 2)
\end {aligned} $$
روش دیگر، در نظر گرفتن اتحاد مزدوج برای دو جمله $$x^3$$ و $$y^ 3 $$ و سپس استفاده از اتحاد چاق و لاغر است:
$$ \large \begin {aligned}
x ^ { 6 } - y ^ { 6 } & = \left ( x ^ { 3 } \right ) ^ { 2 } - \left ( y ^ { 3 } \right ) ^ { 2 } \\
& = \left ( x ^ { 3 } + y ^ { 3 } \right ) \left ( x ^ { 3 } - y ^ { 3 } \right ) \\
& = \left [ ( x + y ) \left ( x ^ { 2 } - x y + y ^ { 2 } \right ) \right ] \left [ ( x - y ) \left ( x ^ { 2 } + x y + y ^ { 2 } \right ) \right ] \\
& = ( x + y ) \left ( x ^ { 2 } - x y + y ^ { 2 } \right ) ( x - y ) \left ( x ^ { 2 } + x y + y ^ { 2 } \right )
\end {aligned} $$
مثال سوم تجزیه عبارت های جبری
عبارت جبری زیر را ساده کنید.
$$ \large x ( 3 x - 5 ) + (-2x+4)x $$
حل: همان‌طور که می‌بینیم، در عبارت بالا، یک $$x$$ مشترک داریم و می‌توانیم از آن فاکتور بگیریم. بنابراین، این عبارت به راحتی به صورت زیر تجزیه می‌شود:
$$ \large \begin {align} x ( 3 x - 5 ) + (-2x+4)x & =x [(3x-5)+(-2x+4)] \\&=x (3x -5-2x+4) \\ &= x ( 3x-2x-5+4) \\ & = x (x-1) \end {align}$$
مثال چهارم تجزیه عبارت های جبری
عبارت جبری زیر را تجزیه کنید.
$$ \large (a+2) (a-3) + 2 a - 6 $$
حل: عبارت $$2a-6$$ را می‌توانیم به صورت $$2(a-3)$$ بنویسیم. سپس خواهیم دید که $$(a-3)$$ مشترک است و عبارت به راحتی تجزیه می‌شود:
$$ \large \begin {align} (a+2) (a-3) + 2 a - 6 & = (a+2)(a-3)+2(a-3) \\ & = (a-3 ) [(a+2)+2] \\
& =(a-3)[a+2+2] \\ &=(a-3)(a+4)
\end {align} $$
مثال پنجم تجزیه عبارت های جبری
عبارت زیر را تجزیه کنید.
$$ \large ( x -4 )^ 2 - x +4 $$
حل: اگر به عبارت بالا دقت کنیم، می‌بینیم که می‌توانیم از $$(x-4)$$ فاکتور بگیریم و آن را به صورت زیر تجزیه کنیم:
$$ \large \begin {align}
( x -4 )^ 2 - x +4 &= (x-4)^ 2 -(x-4)\\
& = (x-4)[(x-4)-1] \\
& = (x-4 )[x-4-1]\\
& = (x-4)(x-5)
\end {align} $$
مثال ششم تجزیه عبارت های جبری
عبارت زیر را تجزیه کنید.
$$ \large { x ^ 2 } + 5 x + 1 $$
حل: عبارت را به صورت زیر می‌نویسیم:
$$ \large { x ^ 2 } + 5 x + 1 = \left ( { x + \underline { \, \, \, \, } } \right ) \left ( { x + \underline { \, \, \, \, } } \right ) $$
اکنون باید دو عدد را پیدا کنیم که مجموع آن‌ها برابر با $$1$$ و حاصل‌ضربشان $$ 5$$ باشد. اما دو عدد صحیح که در چنین شرایطی صدق کنند، وجود ندارند. به همین دلیل، می‌توان گفت که نمی‌توان با اعداد صحیح چندجمله‌ای مرتبه دوم بالا را تجزیه کرد.
مثال هفتم تجزیه عبارت های جبری
عبارت زیر را تجزیه کنید.
$$ \large 3 { x ^ 4 } - 3 { x ^ 3 } - 3 6 { x ^ 2 } $$
حل: مشاهده می‌کنیم که $$ 3x^2$$ در همه جملات وجود دارد. بنابراین، می‌توان از آن فاکتور گرفت و نوشت:
$$ \large 3 { x ^ 4 } - 3 { x ^ 3 } - 3 6 { x ^ 2 } = 3 { x ^ 2 } \left ( { { x ^ 2 } - x - 1 2 } \right ) $$
با کمک اتحاد جمله مشترک، در نهایت چندجمله‌ای به صورت زیر تجزیه می‌شود:
$$ \large 3 { x ^ 4 } - 3 { x ^ 3 } - 3 6 { x ^ 2 } = 3 { x ^ 2 } \left ( { x - 4 } \right ) \left ( { x + 3 } \right ) $$
مثال هشتم تجزیه عبارت های جبری
عبارت زیر را تجزیه کنید.
$$ \large {x^4} - 25 $$
حل: چندجمله‌ای را می‌توانیم به صورت زیر بنویسیم:
$$ \large { x ^ 4 } - 2 5 = { \left ( { { x ^ 2 } } \right ) ^ 2 } - { \left ( 5 \right ) ^ 2 } $$
در نتیجه، با استفاده از اتحاد مزدوج، خواهیم داشت:
$$ \large { x ^ 4 } - 2 5 = \left ( { { x ^ 2 } + 5 } \right ) \left ( { { x ^ 2 } - 5 } \right ) $$
مثال نهم تجزیه عبارت های جبری
عبارت زیر را تجزیه کنید.
$$ \large {x^4} + {x^2} - 20 $$
حل: اگر به چندجمله‌ای بالا دقت کنیم، جمله $$ x ^ 2 $$ آن را می‌توانیم به عنوان یک متغیر در نظر بگیریم و در نتیجه با توان‌هایی پایین‌تر سر و کار داشته باشیم تا ساده‌سازی عبارت آسان‌تر شود. بنابراین، $$ u = x ^ 2 $$ را در نظر می‌گیریم. در نتیجه، $$ {u^2} = {\left( {{x^2}} \right)^2} = {x^4} $$ خواهد بود. بنابراین، چندجمله‌ای به صورت زیر در می‌آید:
$$ \large { x ^ 4 } + { x ^ 2 } - 2 0 = { u ^ 2 } + u - 2 0 $$
این چندجمله‌ای را می‌توان به صورت زیر تجزیه کرد:
$$ \large \begin {align*} { x ^ 4 } + { x ^ 2 } - 2 0 & = { u ^ 2 } + u - 2 0 \\ & = \left ( { u - 4 } \right ) \left ( { u + 5 } \right ) \\ & = \left ( { { x ^ 2 } - 4 } \right ) \left ( { { x ^ 2 } + 5 } \right ) \end {align*} $$
اما این هنوز پایان کار نیست. می‌توانیم $$ x ^ 2 - 4 $$ را با استفاده از اتحاد مزدوج ساده کنیم. در نهایت، چندجمله‌ای مورد نظر به صورت زیر تجزیه خواهد شد:
$$ \large { x ^ 4 } + { x ^ 2 } - 2 0 = \left ( { x - 2 } \right ) \left ( { x + 2 } \right ) \left ( { { x ^ 2 } + 5 } \right ) $$
مثال دهم تجزیه عبارت های جبری
عبارت زیر را تجزیه کنید.
$$ \large { x ^ 2 } + 2 x - 1 5 $$
حل: این مثال، با توجه به اتحادهایی که گفتیم، ساده است. اما برای یادگیری بهتر با جزئیات بیشتری آن را بررسی می‌کنیم. از آنجا که جمله اول $$ x ^ 2 $$ است، می‌دانیم که باید به فرم زیر باشد:
$$ \large { x ^ 2 } + 2 x - 1 5 = \left ( { x + \underline { \,\,\,\, } } \right ) \left ( { x + \underline { \,\,\,\, } } \right ) $$
همچنین، می‌دانیم که $$ x ^ 2 $$ از ضرب $$ x $$ در $$ x $$ به دست می‌آید. بنابراین، اولین جمله هر فاکتور یا عامل را برابر با $$ x $$ قرار می‌دهیم. حال باید دو جمله دیگر را به دست آوریم که جای خالی برای آن‌ها قرار داده‌ایم.
یک راه این است که حالت‌های ممکن را بررسی کنیم. اگر به چندجمله‌ای دقت کنید، یک عدد $$ - 15 $$ دارد. دو عددی که در پی یافتن آن‌ها هستیم، باید حاصل‌ضربی برابر با $$ - 15 $$ داشته باشند. در اینجا اعداد صحیح را بررسی می‌کنیم. ضرب‌های زیر منجر به $$ - 15 $$ می‌شوند:
$$ \large \left ( { - 1 } \right ) \left ( { 1 5 } \right ) \hspace{0.25in} \left ( 1 \right ) \left ( { - 1 5 } \right ) \hspace{0.25in} \left ( { - 3 } \right ) \left ( 5 \right ) \hspace {0.25in} \left ( 3 \right ) \left ( { - 5 } \right ) $$
می‌توانیم چهار حالت ممکن بالا را آزمایش کرده و جواب صحیح را پیدا کنیم. اگر کمی دقت کنیم، می‌توانیم سه مورد از احتمالات بالا را حذف کنیم. بدین صورت که مجموع دو عددی که انتخاب می‌کنیم باید برابر با ضریب $$ x $$ چندجمله‌ای باشد.
با توجه به آنچه گفتیم، چندجمله‌ای به صورت زیر تجزیه می‌شود:
$$ \large { x ^ 2 } + 2 x - 1 5 = \left ( { x - 3 } \right ) \left ( { x + 5 } \right)$$
پس به طور خلاصه، در مواردی که می‌خواهیم یک چندجمله‌ای مرتبه دوم را تجزیه کنیم، باید دو عدد را پیدا کنیم که حاصل‌ضرب آن‌ها برابر با عدد موجود در چندجمله‌ای بوده و حاصل‌جمع آن‌ها برابر با ضریب $$ x $$ چندجمله‌ای باشد. در حقیقت، در این موارد از اتحاد جمله مشترک استفاده می‌کنیم.
