بلوک دیاگرام در مهندسی کنترل — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های پیشین مجله فرادرس، درباره نمایش تابع تبدیل سیستم‌های کنترل بحث کردیم. بلوک دیاگرام یا نمودار بلوکی یکی از ابزارهای مفید برای نمایش تصویری سیستم‌ها و به‌ویژه سیستم‌های کنترل است که رابطه علت و معلولی بین ورودی‌ها و خروجی‌ها را نمایش می‌دهد. گاهی سیستم‌ها پیچیده هستند و از زیرسیستم‌های دیگر تشکیل می‌شوند. به‌دلیل این پیچیدگی، ابتدا زیرسیستم‌ها را نمایش می‌دهند و سپس به یکدیگر متصل می‌کنند. با استفاده از نمودار بلوکی، می‌توان زیرسیستم‌ها را به‌سادگی نمایش داد و با ترکیب آن‌ها نمایش سیستم اصلی را ارائه کرد و با ساده‌سازی آن، به تابع تبدیل سیستم دست یافت. در این آموزش، اجزای اصلی نمودارهای بلوکی و روش ساده‌سازی آن‌ها را توضیح خواهیم داد.

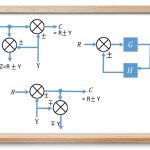
اجزای اصلی نمودار بلوکی

اجزای اساسی یک نمودار بلوکی، بلوک‌ها، نقاط جمع و نقاط انشعاب هستند.

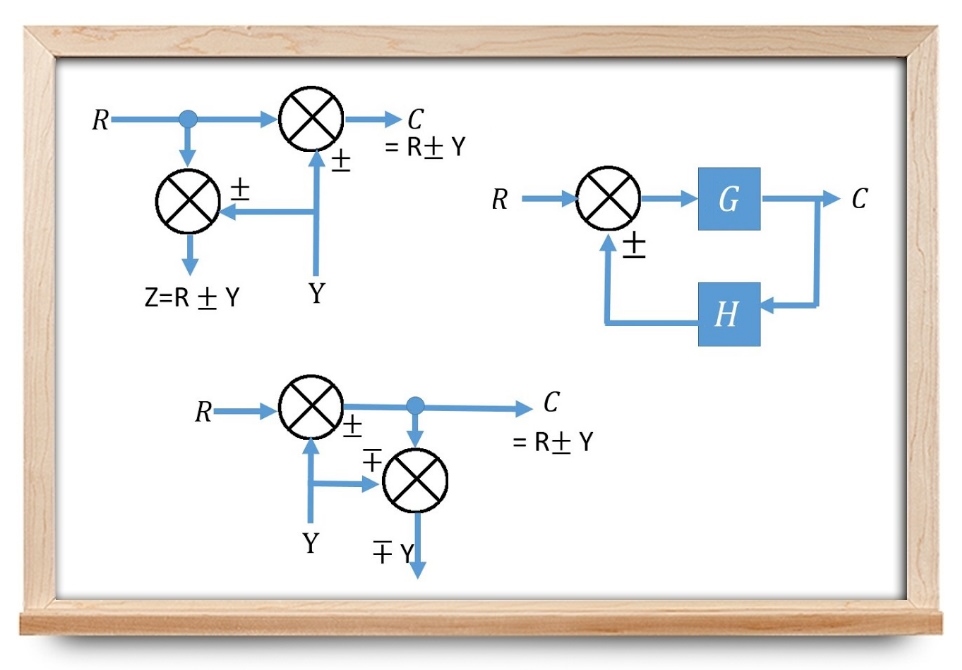
شکل زیر، نمودار بلوکی یک سیستم کنترل حلقه‌بسته را نشان می‌دهد که در آن، اجزا مشخص شده‌اند.

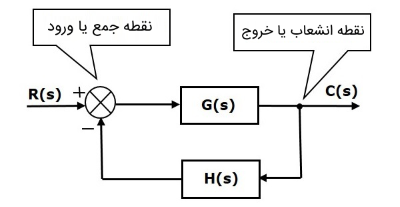
نمودار بالا از دو بلوک با توابع تبدیل (G(s و (H(s تشکیل شده است. این نمودار بلوکی، همچنین یک نقطه جمع و یک نقطه انشعاب دارد. پیکان‌ها جهت گذر سیگنال‌ها را نشان می‌دهند. در ادامه، هریک از اجزا را به‌صورت جداگانه توضیح می‌دهیم.

بلوک

تابع تبدیل یک بخش از سیستم با یک «بلوک» (Block) نشان داده می‌شود. بلوک یک ورودی و یک خروجی دارد. شکل زیر، یک بلوک را با ورودی (X(s و خورجی (Y(s و تابع تبدیل (G(s نشان می‌دهد.

تابع تبدیل به‌صورت زیر تعریف می‌شود:

$$\large G ( s ) = \frac { Y ( s ) } { X ( s ) }$$

خروجی را نیز می‌توان با ضرب تابع تبدیل در ورودی به‌دست آورد:

$$\large Y ( s ) = G ( s ) X ( s )$$

نقطه جمع

«نقطه جمع» (Summing Point)، با یک دایره و علامت ضربدر (X) داخل آن نمایش داده می‌شود و دو یا چند ورودی و یک خروجی دارد. این بخش از نمودار بلوکی، جمع جبری ورودی‌ها را تولید می‌کند. در واقع، نقطه جمع، مجموع، تفریق یا ترکیبِ مجموع و تفریق ورودی‌ها را براساس علامت آن‌ها محاسبه می‌کند. این سه عمل را به‌طور جداگانه بررسی می‌کنیم.

جمع

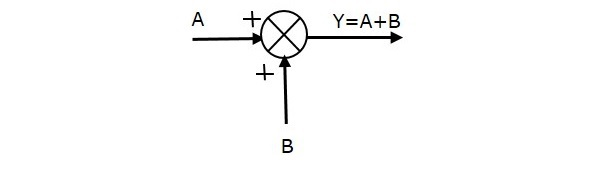
شکل زیر، نقطه جمع را با دو ورودی (A,B) و خروجی (Y) نشان می‌دهد. علامت ورودی‌های A و B مثبت است. بنابراین، خروجی Y نقطه جمع برابر با مجموع A و B است؛ یعنی Y=A+B.

تفریق

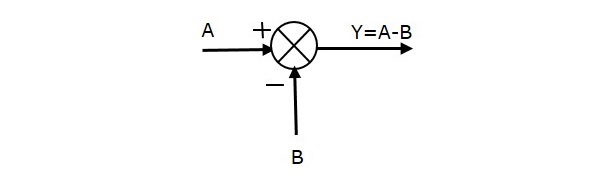
شکل زیر نقطه جمع را با دو ورودی (A,B) و خروجی (Y) نشان می‌دهد. علامت ورودی‌های A و B مخالف یکدیگر (A با علامت مثبت و B با علامت منفی) است. بنابراین، خروجی Y نقطه جمع برابر با اختلاف A و B است؛ یعنی Y = A + (-B) = A - B.

ترکیب

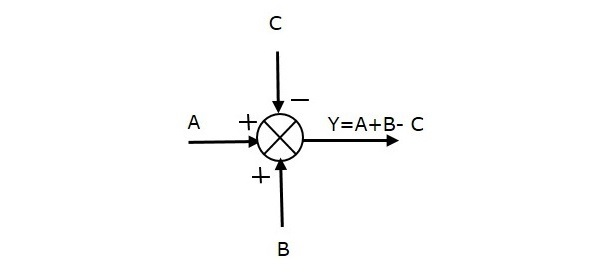
شکل زیر نقطه جمع را با سه ورودی (A, B, C) و خروجی (Y) نشان می‌دهد. علامت ورودی‌های A و B مثبت و علامت ورودی C منفی است. بنابراین، نقطه جمع، خروجی Y را به‌صورت زیر نتیجه می‌دهد:

Y = A + B + (−C) = A + B − C

نقطه انشعاب

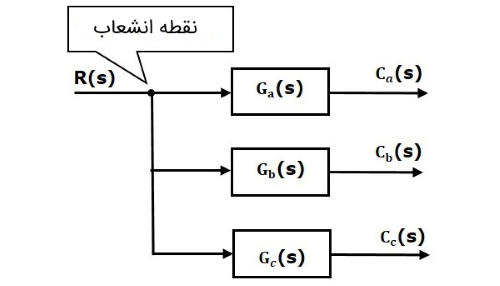
«نقطه انشعاب» (Take-off Point) یا خروج، نقطه‌ای است که ورودی آن می‌تواند به چند شاخه تقسیم شود. این بدین معنی است که با کمک نقطه انشعاب می‌توان یک ورودی را به یک یا چند بلوک یا نقطه جمع اعمال کرد. در شکل زیر، از نقطه انشعاب برای برقراری ارتباط ورودی (R(s با سه بلوک دیگر استفاده شده است.

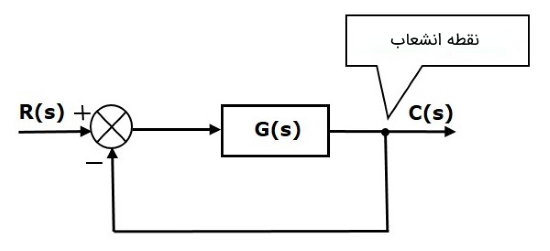
شکل زیر، نقطه انشعاب برای برقراری ارتباط خروجی (C(s (به‌عنوان یکی از ورودی‌های نقطه جمع) با نقطه جمع به‌کار رفته است.

اجزای نمودار بلوکی، در شکل زیر نشان داده شده است:

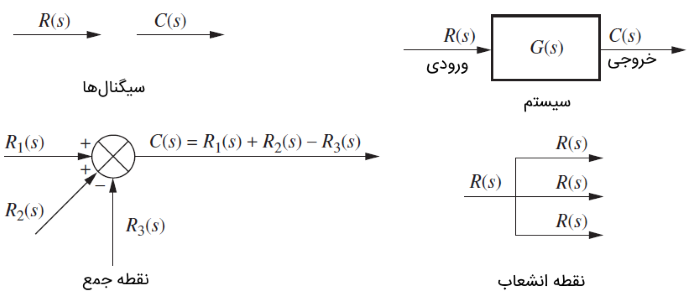
رسم بلوک دیاگرام مدارهای الکتریکی

مدارهای الکتریکی سه عنصر اصلی دارند: مقاومت، خازن و سلف.

مدار RLC سری شکل زیر را در نظر بگیرید که در آن، $$v_i (t)$$ و $$v_o (t)$$ به‌ترتیب، ولتاژهای ورودی و خروجی مدار هستند. فرض می‌کنیم جریان $$i(t)$$ از مدار می‌گذرد.

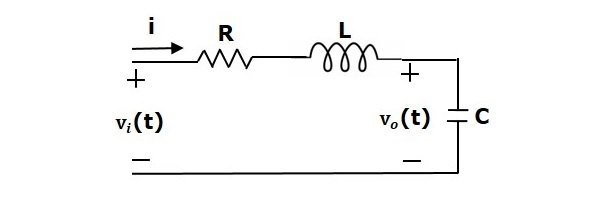
با اعمال تبدیل لاپلاس به مدار، آن را به فضای s می‌بریم که در شکل زیر نشان داده شده است.

با توجه به مدار بالا، داریم:

$$\large I ( s ) = \frac{ V _ i ( s ) - V _ o ( s ) } { R + s L  }$$

$$\large \Rightarrow I ( s ) = \left \{ \frac{ 1 } { R + s L } \right \}\left \{ V _ i ( s ) - V _ o ( s ) \right \} \,\,\,\, \,\,\,\, (1)$$

$$\large V _ o ( s ) = \left ( \frac{ 1 } {  s C } \right ) I ( s ) \,\,\,\, \,\,\,\, (2)$$

اکنون نمودار بلوکی این دو معادله را به‌صورت جداگانه رسم کرده، سپس آن‌ها را با هم ترکیب می‌کنیم و نمودار بلوکی مدار RLC سری را به‌دست می‌آوریم.

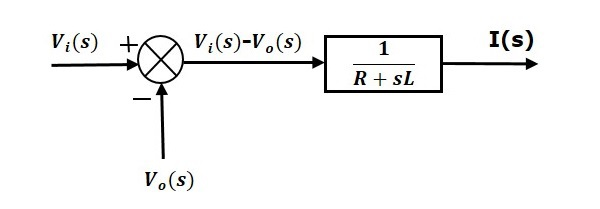
معادله (۱)‌ را می‌توان با یک بلوک با تابع تبدیل $$\frac{1}{R+sL}$$ پیاده‌سازی کرد. ورودی و خروجی این بلوک به‌ترتیب، $$\left \{ V_i(s)-V_o(s) \right \}$$ و $$I(s)$$ هستند. برای تشکیل سیگنال $$\left \{ V_i(s)-V_o(s) \right \}$$، به یک نقطه جمع نیاز داریم. نمودار بلوکی معادله (۱) در شکل زیر نشان داده شده است.

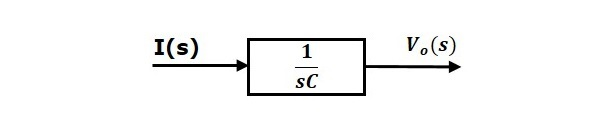
معادله (۲)‌ را می‌توان با نمودار بلوکی با تابع تبدیل $$\frac{1}{sC}$$ پیاده‌سازی کرد. ورودی و خروجی این بلوک به‌ترتیب، $$I(s)$$ و $$V_o(s)$$ هستند. نمودار بلوکی معادله (۲) در شکل زیر نشان داده شده است.

با ترکیب نمودارها، نمودار بلوکی کلی مدار RLC‌ سری (در فضای s) به‌صورت شکل زیر خواهد بود.

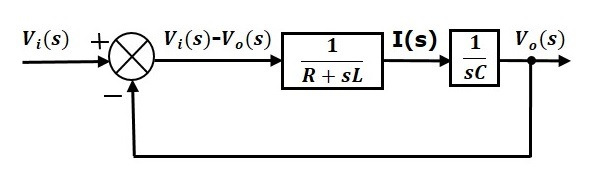
به‌طریق مشابه می‌توان نمودار بلکوی هر مدار یا سیستم الکتریکی را با انجام مراحل زیر به‌دست آورد:

• تبدیل مدار از حوزه زمان به حوزه s با استفاده از تبدیل لاپلاس
• نوشتن معادلات جریان یا ولتاژ مدار
• رسم نمودارهای بلوکی برای تک‌تک معادلات به‌صورت جداگانه
• ترکیب همه بلوک‌ها و به‌دست آوردن نمودار بلوکی نهایی

اتصالات پایه بلوک‌ها

جبر نمودار بلوکی، چیزی جز نمایش تصویری معادلات جبری و روابط بین بلوک‌ها نیست. در ادامه چند مورد از اتصالات مهم بلوک‌ها را بررسی می‌کنیم.

اتصال سری یا متوالی

اتصال سری که اتصال آبشاری نیز نامیده می‌شود، بین دو تابع تبدیل $$G_1 (s)$$ و $$G_ 2 (s)$$ در شکل زیر نشان داده شده است.

در این نوع اتصال، خروجی $$Y(s)$$ به‌صورت زیر خواهد بود:

$$\large Y ( s ) = G _ 2 ( s ) Z ( s )$$

که در آن $$Z(s)=G_1(s)X(s)$$ است. بنابراین، داریم:

$$\large \Rightarrow Y ( s ) = G _ 2 ( s )[ G _ 1 ( s ) X ( s ) ] = G _ 1 ( s ) G _ 2 ( s ) X ( s ) \\ \large \Rightarrow Y ( s ) = \lbrace G _ 1 ( s ) G _ 2 ( s ) \rbrace X ( s )$$

با مقایسه رابطه اخیر با فرم استاندارد معادله خروجی $$Y(s)=G(s)X(s)$$، به رابطه زیر خواهیم رسید:

 $$\large G ( s ) = G _ 1 ( s ) G _ 2 ( s )$$

رابطه اخیر بدین معنی است که در اتصال متوالی، دو بلوک را می‌توان به‌صورت یک بلوک نوشت. همان‌طور که دیدم، تابع تبدیل متناظر با این بلوک معادل، برابر با حاصل‌ضرب توابع تبدیل متوالی است. برای بیش از دو تابع تبدیل متوالی نیز این رابطه برقرار است.

اتصال موازی

ورودی دو بلوک موازی، یکسان است. در شکل زیر، دو بلوک موازی با توابع تبدیل $$G_1(s)$$ و $$G_2 (s)$$ نشان داده شده است. خروجی این دو تابع تبدیل به نقطه جمع وارد می‌شود.

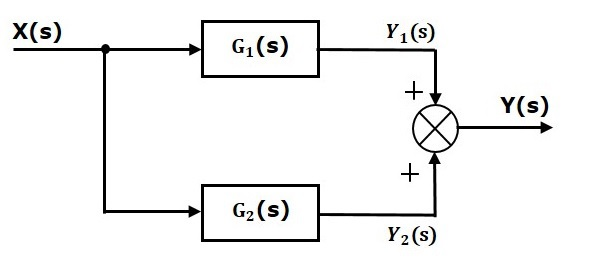
برای این ترکیب،‌ خروجی $$Y (s)$$ به‌صورت زیر خواهد بود:

$$\large Y ( s ) = Y _ 1 ( s ) + Y _ 2 ( s )$$

که در آن:

$$\large Y _ 1 ( s ) = G _ 1 ( s ) X ( s )$$

و

$$\large Y _ 2 ( s )  = G _ 2 ( s ) X ( s )$$

بنابراین:

$$\large Y ( s ) = G _ 1 ( s ) X ( s ) + G _ 2 ( s ) X ( s ) = \lbrace G _ 1 ( s ) + G _ 2 ( s ) \rbrace X ( s )$$

با مقایسه این معادله و فرم استاندارد $$Y(s)=G(s)X(s)$$، به رابطه زیر می‌رسیم:

$$\large G ( s ) = G _ 1 ( s ) + G  _ 2 (  s )$$

رابطه اخیر، بدین معنی است که می‌توانیم ترکیب موازی دو بلوک را با یک بلوک جایگزین کنیم که تابع تبدیل آن، برابر با مجموع توابع تبدیل دو بلوک موازی است. بلوک معادل در شکل زیر نشان داده شده است:

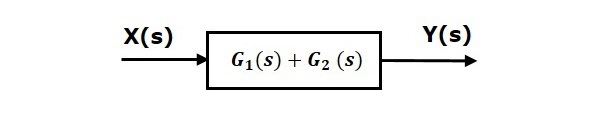
به‌طریق مشابه، تعداد $$n$$ بلوک موازی را نیز می‌توان با یک بلوک معادل نشان داد که تابع تبدیل آن برابر با مجموع توابع تبدیل $$n$$ بلوک است.

اتصال فیدبک

همان‌طور که در آموزش مربوط به فیدبک در سیستم‌های کنترل اشاره کردیم، دو نوع فیدبک مثبت و فیدبک منفی وجود دارد. شکل زیر، نمودار بلوکی یک سیتم کنترل با فیدبک منفی را نشان می‌دهد. در این نمودار، دو تابع تبدیل $$G(s)$$ و $$H(s)$$ یک سیستم حلقه‌بسته را تشکیل می‌دهند.

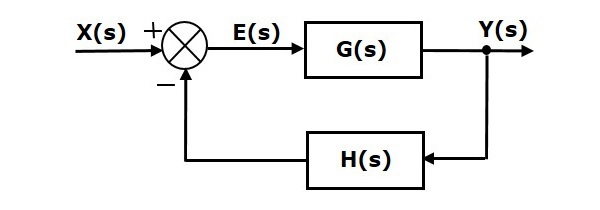
حاصل نقطه جمع برابر است با:

$$\large E ( s ) = X ( s ) - H ( s ) Y ( s )$$

برای خروجی $$Y(s)$$ نیز داریم:

$$\large Y ( s ) =  E ( s ) G ( s )$$

با جایگذاری مقدار $$E(s)$$ در معادله اخیر، خواهیم داشت:

$$\large Y ( s ) = \left \{ X ( s ) - H ( s ) Y ( s ) \rbrace G ( s ) \right\} \\ \large Y ( s ) \left \{ 1 + G ( s ) H ( s )\rbrace = X ( s ) G ( s ) \right\} \\ \large \Rightarrow \frac{ Y ( s ) } { X ( s ) } = \frac{ G ( s ) }{ 1 + G ( s ) H ( s ) }$$

بنابراین، تابع تبدیل حلقه‌بسته فیدبک منفی برابر است با:

$$\large \frac{ G (  s ) } { 1 +  G ( s ) H ( s ) }$$

فرمول اخیر بدین معنی است که یک اتصال فیدبک منفی را می‌توان با بلوکی که تابع تبدیل آن مطابق فرمول اخیر است خلاصه کرد. شکل زیر، این بلوک معادل را نشان می‌دهد.

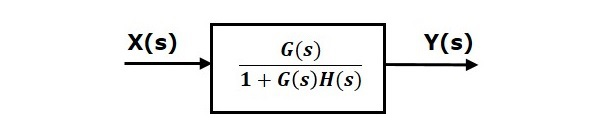
به‌طریق مشابه می‌توان دو بلوک را که اتصال آن‌ها به‌صورت فیدبک مثبت است، با یک بلوک معادل نشان داد که تابع تبدیل آن، به‌صورت زیر خواهد بود:

$$\large \frac{ G ( s ) } { 1 -  G ( s ) H ( s ) }$$

جبر نمودار بلوکی برای نقاط جمع و انشعاب

جبر نقاط جمع و انشعاب در نمودارهای بلوکی، به‌معنی جابه‌جایی نقاط جمع و انشعاب است که معمولاً‌ برای ساده‌سازی نمودار انجام می‌شود. در ادامه، این جبر بلوکی را برای نقاط جمع و انشعاب بیان خواهیم کرد.

جبر نمودار بلوکی برای نقاط جمع

با توجه به قرارگیری بلوک‌ها، به دو صورت می‌توان نقاط جمع را جابه‌جا کرد:

• جابه‌جایی نقطه جمع به بعد از بلوک
• جابه‌جایی نقطه جمع به قبل از بلوک

جابه‌جایی نقطه جمع به بعد از بلوک

نمودار بلوکی زیر را در نظر بگیرید که در آن، نقطه جمع قبل از بلوک قرار دارد.

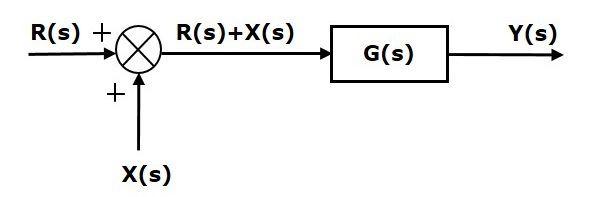
نقطه جمع شکل بالا، دو ورودی $$R(s)$$ و $$X(s)$$ دارد و خروجی آن $$\left \{R(s)+X(s)\right\}$$ است. خروجی نمودار بلوکی نیز برابر است با:

$$\large Y ( s ) = G ( s ) \left \{ R ( s )  + X ( s ) \right \}$$

$$\large \Rightarrow Y (  s ) = G ( s ) R ( s ) + G ( s ) X ( s ) \,\,\,\,\,\,\,\, (3)$$

اکنون نقطه جمع را به بعد از بلوک جابه‌جا می‌کنیم. نمودار بلوکی حاصل از این کار به‌صورت زیر است:

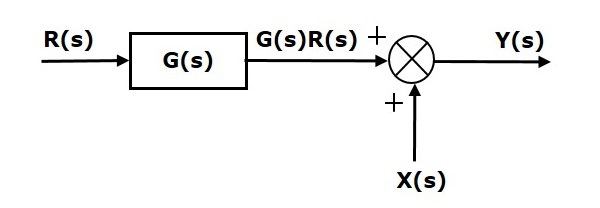
بنابراین، خروجی بلوک $$G(s)$$ برابر با $$G(s)R(s)$$ خواهد بود.

خروجی نقطه جمع برابر است با:

$$\large Y ( s ) = G ( s ) R ( s ) + X ( s )  \,\,\,\,\,\,\,\, (4)$$

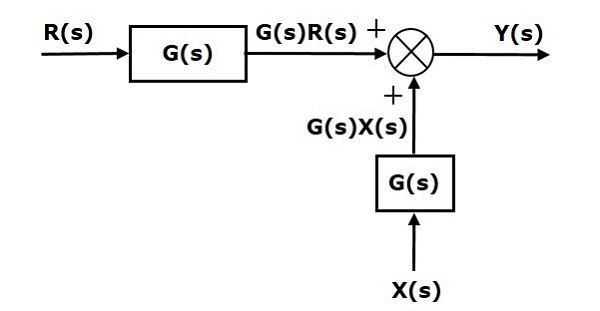
اکنون معادله‌های (۳) و (۴) را با یکدیگر مقایسه می‌کنیم. همان‌طور که می‌بینیم، جمله اول $$G(s) R(s)$$ در دو معادله یکسان است. اما، در جملات دوم تفاوت وجود دارد. برای آنکه جملات دوم با هم مشابه شوند، به بلوک $$G(s)$$ نیاز داریم. ورودی این بلوک $$X(s)$$ است و خروجی آن به‌عنوان ورودی به نقطه جمع وارد می‌شود. نمودار بلوکی مورد نظر به‌صورت شکل زیر است.

جابه‌جایی نقطه جمع به قبل از بلوک

نمودار بلوکی شکل زیر را در نظر بگیرید. در این شکل، نقطه جمع بعد از بلوک قرار دارد.

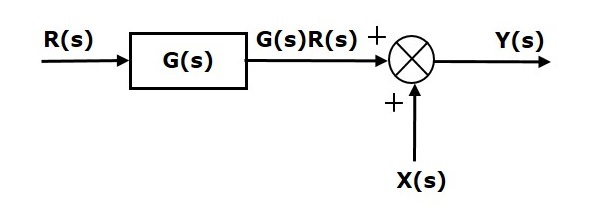
خروجی این نمودار بلوکی، برابر است با:

$$\large Y ( s ) = G ( s ) R ( s ) + X ( s ) \,\,\,\,\,\,\,\, (5)$$

اکنون نقطه جمع را به قبل از بلوک انتقال می‌دهیم. نمودار بلوکی حاصل به‌صورت شکل زیر است.

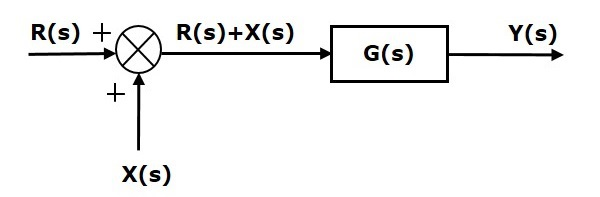
خروجی نمودار بلوکی شکل بالا به‌صورت زیر است:

$$\large Y ( S ) = G ( s ) R ( s ) + G ( s ) X ( s ) \,\,\,\,\,\,\,\, (6)$$

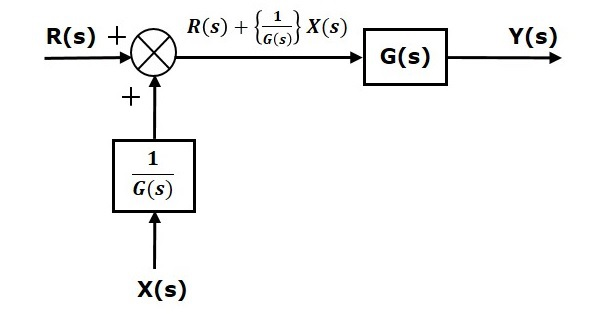
روابط (۵) و (۶) را با هم مقایسه می‌کنیم. جمله اول $$G(s) R(s)$$ در دو معادله مشابه است. اما،‌در جمله دوم تفاوت وجود دارد. برای آنکه جملات دوم دو معادله نیز با هم برابر باشند، به بلوک $$\frac{1}{G(s)}$$ نیاز داریم. ورودی این بلوک $$X(s)$$ است و خروجی آن، به‌عنوان ورودی به‌جای $$X(s)$$ به نقطه جمع وارد می‌شود. نمودار بلوکی معادل در شکل  زیر نشان داده شده است.

جبر نمودار بلوکی برای نقاط انشعاب

با توحه به قرارگیری بلوک‌ها، به دو صورت می‌توان نقاط انشعاب را جابه‌جا کرد:

• جابه‌جایی نقطه انشعاب به بعد از بلوک
• جابه‌جایی نقطه انشعاب به قبل از بلوک

جابه‌جایی نقطه انشعاب به بعد از بلوک

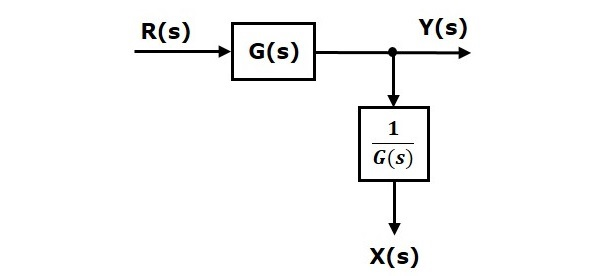
نمودار بلوکی شکل زیر را در نظر بگیرید که در آن، نقطه انشعاب قبل از بلوک قرار دارد.

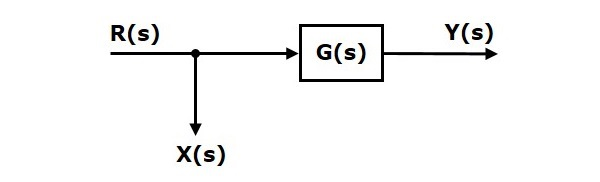
در نمودار بالا، روابط $$X(s)=R(s)$$ و $$Y(s)=G(s)R(s)$$ را داریم. وقتی نقطه انشعاب به بعد از بلوک جابه‌جا می‌شود، خروجی $$Y(s)$$ تغییر نمی‌کند. اما در مقدار $$X(s)$$ تفاوت وجود دارد. بنابراین، برای آنکه $$X(s)$$ برابر با حالت قبل باشد، به یک بلوک $$\frac{1}{G(s)}$$ نیاز داریم. با قرار دادن این بلوک، نمودار بلوکی شکل زیر به‌دست می‌آید.

جابه‌جایی نقطه انشعاب به قبل از بلوک

نمودار بلوکی شکل زیر را در نظر بگیرید که در آن، نقطه انشعاب بعد از بلوک قرار دارد.

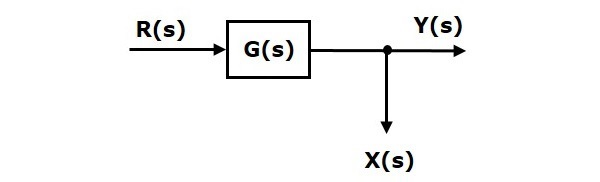
در نمودار بلوکی شکل بالا، رابطه زیر برقرار است:

$$\large X ( s ) = Y ( s ) = G ( s ) R ( s )$$

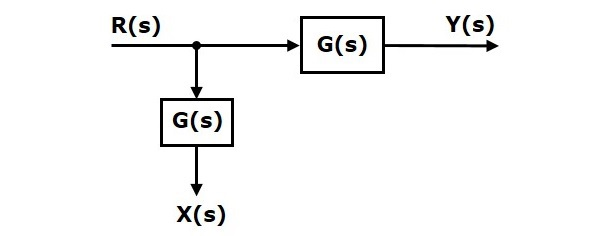
اگر نقطه انشعاب را به قبل از بلوک انتقال دهیم،‌ خروجی $$Y(s)$$ تغییری نمی‌کند. اما مقدار $$X(s)$$ تغییر خواهد کرد. بنابراین، برای آنکه $$X(s)$$ مشابه حالت قبل باقی بماند، به بلوک $$G(s)$$ نیاز داریم که ورودی آن $$R(s)$$ و خروجی آن $$X(s)$$ است. نمودار بلوکی جدید در شکل زیر نشان داده شده است:

قواعد ساده‌سازی نمودارهای بلوکی

چند قاعده ساده وجود دارد که با استفاده از آن‌ها می‌توان نمودارهای بلوکی با بلوک‌ها، نقاط جمع و نقاطط انشعاب زیاد را اصطلاحاً کاهش داد یا ساده کرد. این قواعد به‌صورت زیر هستند:

• قاعده ۱: بلوک‌های سری یا متوالی را با یک بلوک معادل جایگزین کنید.
• قاعده ۲: بلوک‌های موازی را با یک بلوک معادل جایگزین کنید.
• قاعده ۳: بلوک‌هایی با اتصال فیدبک را پیدا کرده و بلوک معادل آن‌ها را قرار دهید.
• قاعده ۴: در صورت لزوم، نقطه انشعاب را جابه‌جا کنید.
• قاعده ۵: در صورت لزوم، نقطه جمع را جابه‌جا کنید.
• قاعده ۶: قواعد بالا را تا جایی اعمال کنید که به ساده‌ترین حالت، یعنی یک بلوک برسید.

مثال

نمودار بلوکی شکل زیر را در نظر بگیرید. می‌خواهیم با استفاده از قواعدی که بیان شد، این نمودار را ساده کنیم.

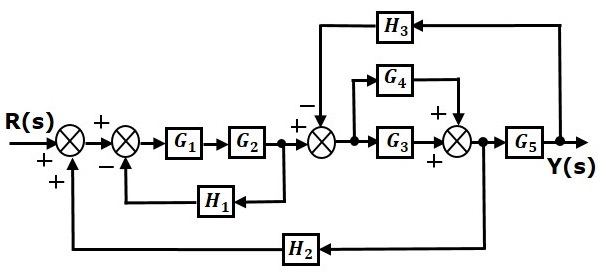
مرحله ۱: از قاعده ۱ برای بلوک‌های $$G_1$$ و $$G_2$$ استفاده می‌کنیم. قاعده ۲ را نیز برای $$G_3$$ و $$G_4$$ به‌کار می‌بریم. نمودار اصلاح‌شده به‌صورت زیر خواهد بود:

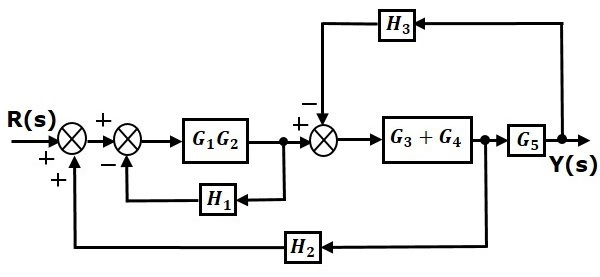
مرحله ۲: بلوک‌های $$G_1G_2$$ و $$H_1$$ اتصال فیدبک دارند و می‌توانیم از قاعده ۳ برای آن‌ها استفاده کنیم. با کمک قاعده ۴، نقطه انشعاب قبل از بلوک $$G_5$$‌ را به بعد از آن جابه‌جا می‌کنیم. در نتیجه، به نمودار بلوکی زیر خواهیم رسید.

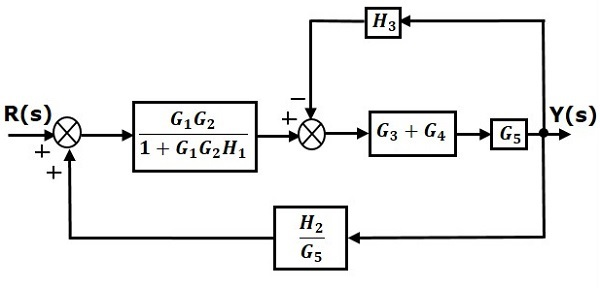
مرحله ۳: می‌بینیم که بلوک‌های $$G_3+G_4$$ و $$G_5$$ سری هستند، بنابراین، قاعده ۱ را به آن‌ها اعمال می‌کنیم.

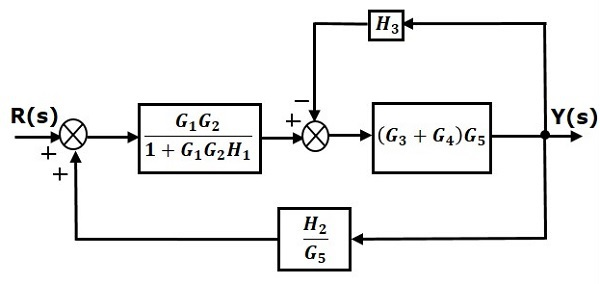
مرحله ۴: با استفاده از قاعده ۳، بلوک‌های $$(G_3 + G_4)G_5$$ و $$H_3$$ را که اتصال فیدبک دارند، به یک بلوک کاهش می‌دهیم.

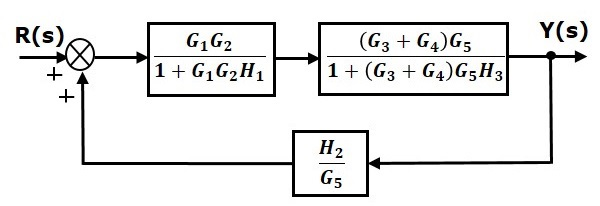
مرحله ۵: از قاعده ۱ استفاده می‌کنیم و به نمودار بلوکی شکل زیر می‌رسیم:

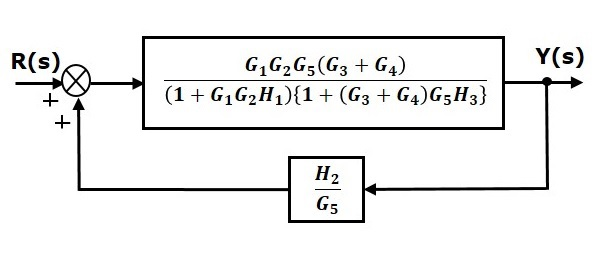
مرحله ۶: اتصال نمودار بلوکی اخیر، فیدبک مثبت است، با استفاده از قاعده ۳، این اتصال را می‌توان با بلوک معادل زیر جایگزین کرد:

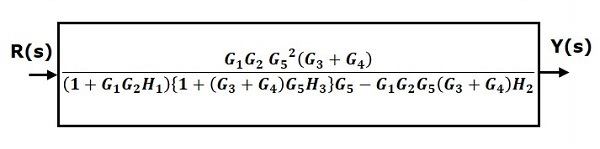
بنابراین، تابع تبدیل سیستم برابر است با:

$$\large \frac { Y ( s ) } { R ( s ) } = \frac { G _ 1 G _ 2 G _ 5 ^ 2 ( G _ 3 + G _ 4 ) } { ( 1 + G _ 1 G _ 2 H _ 1 ) \lbrace 1 +( G _ 3 + G _ 4 ) G _ 5 H _ 3 \rbrace G _ 5 - G _ 1 G _ 2 G _ 5 ( G _ 3 + G _ 4 ) H _ 2 }$$

فرایند ساده‌سازی نمودار بلوکی برای سیستم‌های پیچیده، زمان‌بر است. زیرا در هر مرحله باید نمودار را رسم کنیم. برای غلبه بر این مشکل، از نموادار گذر سیگنال استفاده می‌شود که در آموزش‌های بعدی، آن را معرفی می‌کنیم.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• نمایش سیستم های دینامیکی با متلب — از صفر تا صد
• سیستم کنترل حلقه باز — به زبان ساده
• مکان هندسی ریشه ها (Root Locus) در مهندسی کنترل — به زبان ساده

^^