اصل دالامبر – به زبان ساده

پیش‌تر در وبلاگ فرادرس در مورد مفاهیم مربوط به قوانین نیوتن صحبت شد. هم‌چنین در مطلب ارتعاشات نحوه بدست آوردن معادله ارتعاشی یک سیستم را با استفاده از قوانین نیوتن بیان کردیم. در این مطلب قصد داریم تا اصل دالامبر را توضیح دهیم.

البته به منظور درک بهتر مطلب پیشنهاد می‌شود مطالب لختی دورانی، قوانین نیوتن و معادله اویلر لاگرانژ را مطالعه کنید.

مقدمه

اصل دالامبر یا اصل لاگرانژ-دالامبر بیان کننده قوانین پایه‌ای حرکت در مکانیک کلاسیک است. به منظور درک این اصل لازم است تا در ابتدا با قانون کار مجازی آشنا باشید.

قانون کار مجازی

قانون کار مجازی بیان می‌کند که مجموع کار انجام شده توسط نیرو‌های خارجی وارد به یک سیستم برابر با صفر است. در حقیقت در این حالت سیستمی در نظر گرفته شده که چند نیروی مجازی به آن وارد می‌شود. هریک از این نیرو‌ها نقطه‌ای از سیستم را به اندازه $$\large \delta _ { s i }$$ جابجا می‌کند. مجموع کار انجام شده در نتیجه هریک از این جابجایی‌ها برابر است با:

$$\Large \delta W = \sigma F _ i . \delta s _ i = 0$$

تکنیک کار مجازی در حل مسائل استاتیک بسیار کاربرد دارد. در یک مسئله استاتیکی، شتابی وجود ندارد. با این حال، این قانون را می‌توان به مسائل دینامیکی نیز تعمیم داد. توجه داشته باشید که در مسائل دینامیکی از مفهوم لختی یا اینرسی استفاده می‌شود. برای هر بخش از یک سیستم، می‌توان قانون دوم نیوتن را به صورت زیر بیان کرد.

$$\Large F = m a$$

این مسئله دینامیکی را می‌توان با استفاده از تعریف یک نیروی اینرسی، به مسئله‌ای استاتیکی تبدیل کرده و آن را تحلیل کرد. این نیرو به صورت زیر تعریف می‌شود.

$$\Large F ^ *= - m a$$

از این رو قانون دوم نیوتن را می‌توان به صورت زیر بیان کرد.

$$\Large F_{total} = F + f^ * = 0$$

اصل دالامبر معادل با اصل کار مجازی به همراه نیرو‌های اینرسی است که کار انجام می‌دهند. با اضافه شدن دیفرانسیل نیروی اینرسی، نهایتا اصل دالامبر به صورت زیر قابل بیان خواهد بود.

$$\Large \boxed { \delta W = \Sigma F_ i. \delta s_i + \Sigma^ * _ j. \delta s_j = 0 }$$

در ادامه، مسئله سقوط آزاد یک جرم با استفاده از اصل دالامبر مورد بررسی قرار گرفته است.

سقوط آزاد

جسمی به جرم m را تصور کنید که تحت میدان گرانشی g در حال سقوط است. با فرض این که جهت مثبت z به سمت بالا باشد، نیروی وارد شده به جرم برابر با $$\large - m g$$ است. اگر این جرم به اندازه $$\delta z$$ جابجا شود، کار انجام شده در نتیجه نیروی گرانشی برابر $$\delta W _ G = - m g \delta z$$ است. از طرفی نیروی اینرسی وارد شده به جرم برابر با $$- m \frac {d ^ 2 z } { d t ^2 }$$ بوده، در نتیجه کار نیروی اینرسی برابر است با:

$$\large \delta W _ l = - m \frac {d ^ 2 z } { d t ^2 } \delta z$$

مجموع کار انجام شده توسط دو نیروی اینرسی و گرانشی برابر با صفر است. بنابراین می‌توان گفت:

$$\large -mg \delta z – m \frac { d ^ 2 z } { d t ^ 2 } \delta z = - [ m g + m \frac {d ^ 2 z } {d t ^ 2 } ]\delta z = 0$$

با ساده‌ سازی عبارت فوق، رابطه مربوط به شتاب گرانشی زمین بدست می‌آید.

$$\large \frac { d ^ 2 z } { d t ^ 2 } = - g$$

مهره و حلقه

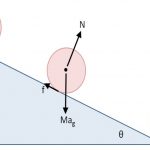
مطابق با شکل زیر سیستمی بدون اصطکاک را در نظر بگیرید. این سیستم از جرم m و یک حلقه تشکیل شده است.

همان‌طور که در تصویر فوق نیز می‌توان دید، نیروی گرانشی الزاما در همه جای سیستم در جهت حرکت نیست. بنابراین مولفه‌ای از نیروی گرانشی که عمود به حلقه است، کاری انجام نمی‌دهد. هم‌چنین نیروی حلقه که حرکت سیستم را به صورت دایره‌ای نگه داشته، کاری انجام نمی‌دهد. کار انجام شده ناشی از نیروی گرانشی در جابجایی اندک $$\delta s = R \delta \phi$$ برابر است با:

$$\Large \delta W _ G = -m g R sin \phi \ \delta \phi$$

تسمه دارای دو شتاب در جهات شعاعی و مماسی است. شتاب شعاعی برابر است با:

$$\Large a _ r = \frac {- v ^ 2 }{ r }$$

در رابطه فوق v نشان دهنده سرعت مماسی بوده و اندازه آن برابر با مقدار زیر است.

$$\Large v = \frac { d s } { d t } = R \frac { d \phi } { d t }$$

به همین صورت اندازه شتاب مماسی برابر با عبارت زیر بدست می‌آید.

$$\Large a_t = \frac {d ^ 2 s } { d t ^ 2} = R \frac { d ^ 2 \phi}{ d t ^ 2 }$$

توجه داشته باشید که نیروی اینرسیِ $$\frac { m v ^ 2 } { R }$$ به دلیل عمود بودن به مسیر حرکت، کاری انجام نمی‌دهد. از طرفی کار انجام شده توسط نیروی اینرسی $$-m a _ t = - m R \frac { d ^ 2 \phi } { d t ^ 2 }$$ برابر است با:

$$\Large \delta W _ l = -m R \frac {d ^ 2 \phi}{d t ^ 2} \delta s = - m R ^2 \frac {d^2 \phi}{ d t ^ 2 }\delta \phi$$

با استفاده از اصل دالامبر، مجموع کار انجام شده توسط این دو نیرو را مطابق با رابطه زیر برابر با صفر قرار می‌دهیم.

$$\large [- m g R \sin \phi – m R ^2 \frac {d ^ 2 \phi } { d t ^ 2 } ] \delta \phi = 0$$

نهایتا با مرتب کردن عبارت فوق، معادله دیفرانسیل توصیف کننده این سیستم به صورت زیر بدست می‌آید.

$$\Large \frac { d ^ 2 \phi } { d t ^ 2} + \frac { g sin \phi } { R } =0$$

نکته: عبارت فوق را می‌توان بر حسب s نیز بیان کرد.

مجموعه‌ای از نیرو‌ها

تاکنون حالت‌هایی را بررسی کردیم که در آن‌ها تعداد معدودی از نیرو‌ها به یک سیستم وارد شدند. البته در حالتی که تعداد نیرو‌ها در یک سیستم استاتیکی یا دینامیکی افزایش یابد، معادلات مربوط به کار مجازی یا اصل دالامبر پیچیده‌تر خواهند شد. در این قسمت از این مطلب قصد داریم تا به صورت دیفرانسیلی یه یک سیستم نگاه کرده و اصل دالامبر را برای کل مجموعه بنویسیم.

فیلم آموزش مکانیک تحلیلی ۱ مرور و حل مثال در فرادرس

کلیک کنید

سقوط آزاد

در ابتدا مسئله سقوط آزاد یک دیسک را دوباره و از زاویه‌ای متفاوت بررسی می‌کنیم. جرمی در حال سقوط را در نظر بگیرید. این جرم فقط حرکتی خطی را تجربه می‌کند در نتیجه جابجایی آن دربازه زمانی dt برای تمامی المان‌ها برابر با dz است.

با فرض این‌که دیفرانسیل‌های جرم به صورت $$\large \Delta m _ i$$ در نظر گرفته شوند، کار انجام شده توسط گرانش در جابجایی dz برابر است با:

$$\Large \delta W _ {G i } = - \Delta m _ i g \delta z$$

از طرفی دیفرانسیل کار انجام شده برای هریک از دیفرانسیل‌های جرمی نیز به صورت زیر محاسبه می‌شود.

$$\Large \delta W _ { I i } = \Delta m _ i \frac { d ^ 2 z } { d t ^ 2 } \delta z$$

توجه داشته باشید که ترم $$\large \frac { d ^ 2 z_ i } { d t ^ 2 }$$ نشان دهنده شتاب هریک از نقاط جسم است. البته در این مثال این مقدار برای تمامی دیفرانسیل‌ها، مقداری برابر است. توجه داشته باشید که اگر بخواهیم این مسئه را دقیق‌تر بررسی کنیم، باید نیرو‌یی که هریک از دیفرانسیل‌ها به هم وارد می‌کنند نیز لحاظ شوند؛ البته این نیرو‌ها طبق قانون سوم نیوتن دو به دو به هم وارد شده و نهایتا یکدیگر را خنثی می‌کنند، از این رو در رابطه، این نیرو‌ها مشاهده نمی‌شوند. نهایتا با جمع زدن دو نیروی اینرسی و نیروی گرانشی وارد به هریک از این دیفرانسیل‌ها خواهیم داشت:

$$\large \delta W = - (g+ \frac { d ^ 2 z } { d t ^ 2 } ) \Sigma \Delta m_i \delta z = - (g+\frac { d ^ z } { d t ^ 2 } ) m \delta _ z$$

همان‌طور که در رابطه فوق نیز نشان داده شده، مجموع جرم‌ها با m نشان داده شده که برابر با جرم جسم است. نهایتا با صفر قرار دادن رابطه بالا، نتیجه‌ای مشابه با حالت قبل بدست می‌آید که در ادامه ذکر شده.

$$\Large \frac { d ^ 2 z } { d t ^ 2 } = - g$$

دیسک چرخان و گشتاور اینرسی

در این قسمت مطابق با شکل زیر فرض می‌کنیم سیستم مورد بررسی، دیسکی است که در حال دوران نیز است.

به طور دقیق‌تر فرض بر این است که نیروی F به سمت راست دیسک وارد می‌شود. کار انجام شده در نتیجه چرخش دیسک به اندازه $$\large d\phi$$، برابر است با:

$$\Large \delta W_F = RF \delta \phi$$

از طرفی کار انجام شده از طرف نیروی اینرسی وارد به دیفرانسیل dm_i برابر با عبارت زیر بدست می‌آید.

$$\Large \delta W _ {I i } = -dm_i r_i \frac {d^2 \phi}{ d t ^ 2 } r _ i \delta \phi$$

در رابطه فوق، r_i نشان دهنده فاصله‌ای است که در آن المان iام قرار گرفته است. همانند حالت قبل، نیرو‌های درونی را نادیده می‌گیریم. نهایتا مجموع کار مجازی برابر است با:

$$\Large \delta W = [R F - \sum_i d m _ i r _ i ^ 2 ( \frac { d ^ 2 \phi } { d t ^ 2 } )] \delta \phi$$

با صفر قرار دادن رابطه فوق، به عبارت زیر می‌رسیم.

$$\Large I \frac { d ^ 2 \phi } { d t ^2 } = R F$$

در رابطه بالا، I به عنوان گشتاور لختی یا لختی دورانی شناخته شده و به صورت زیر تعریف می‌شود.

$$\Large I = \sum _ i d m _ i r _ i ^ 2$$

برای نمونه لختی دورانی برای دیسکی به شعاع R، ضخامت z و چگالی ρ را می‌توان به صورت زیر بدست آورد.

$$\Large I = \rho \int _ 0 ^ w \int _ 0 ^ { 2 \pi } \int _ 0 ^ R r ^ 3 dr d\phi dz = \frac {\pi w R ^ 4 \rho } { 2 }$$

با استفاده از رابطه $$\large M = \pi R ^ 2 w \rho$$، رابطه فوق را می‌توان به صورت زیر بیان کرد:

$$\large I = \frac { M R ^ 2 } { 2 }$$

قضیه محور‌های موازی

با استفاده از این قضیه می‌توان لختی دورانی را حول هر محور دلخواهی بدست آورد. فرض کنید لختی دورانی جسمی به جرمِ M حول مرکز جرمش برابر با I_CM باشد در این صورت لختی دورانی حول محوری با فاصله d از مرکز جرمِ جسم برابر است با:

$$\large I = I_ { C M } +M d ^ 2$$

دیسک غلتان روی سطح شیبدار

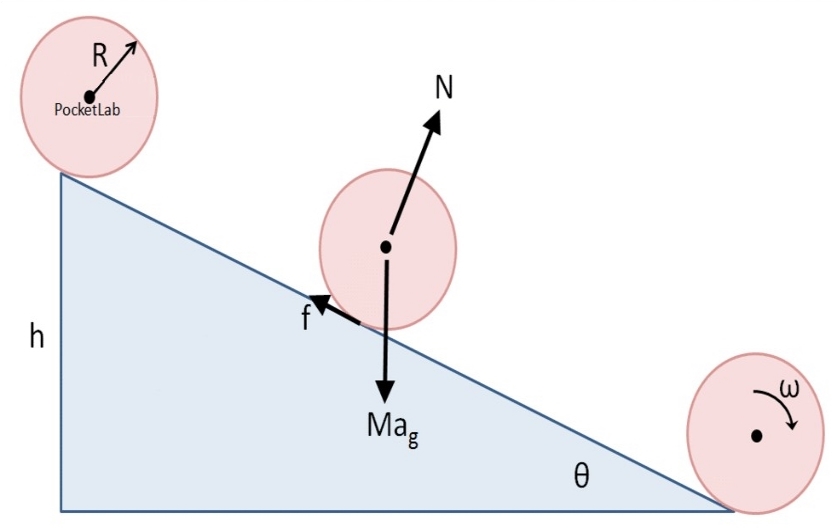
در ابتدا مطابق با شکل زیر، سطحی شیبدار را در نظر می‌گیریم که دیسکی نیز روی آن در حال غلتش است.

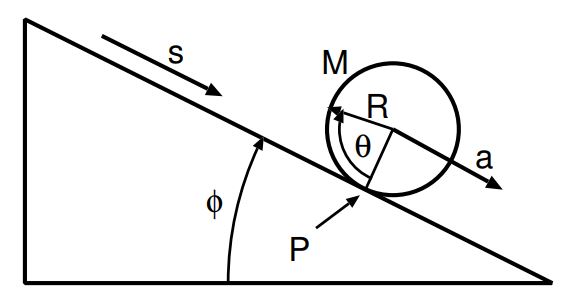
مطابق با شکل فوق دو نیروی لختی و گرانش روی این سیستم کار انجام می‌دهند. اندازه این کار‌ها برابرند با:

$$\Large \delta W _ G = Mg \sin \phi \delta s \ \ \ \ , \ \ \ \ \delta W_ I = - I \frac { d ^ 2 \theta } { d t ^ 2 } \delta \theta$$
رابطه ۱

توجه داشته باشید که نقطه P ساکن است. از این رو معادلات فوق حول نقطه مذکور نوشته شده است. از این رو لختی دورانی نیز باید حول این نقطه محاسبه شود. طبق قضیه محور‌های موازی داریم:

$$\Large I = M R ^ 2 + \frac { M R ^2 } { 2 }$$

نهایتا رابطه ۱ را می‌توان به صورت زیر بیان کرد:

$$\Large \delta W = M g R \sin \phi - \frac { 3 M R ^ 2 }{2} \frac {d ^ \theta } { d t ^ 2 }$$

بدیهی است که در رابطه بالا مقدار $$\large d s$$ برابر با $$d s = R d \theta$$ است. بنابراین معادله دیفرانسیل این سیستم به صورت زیر بدست می‌آید.

$$\Large \frac { d ^ 2 s } { d t ^ 2 } = \frac {2 g \sin \phi } { 3 }$$

رابطه فوق نشان می‌دهد که شتاب دیسک روی سطح شیبدار کمتر از شتاب گرانشی است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• دینامیک موشک با جرم متغیر — به زبان ساده
• حرکت دایره ای - به زبان ساده
• قانون اول ترمودینامیک — به زبان ساده

^^