یخچال کارنو و پمپ حرارتی کارنو – به زبان ساده

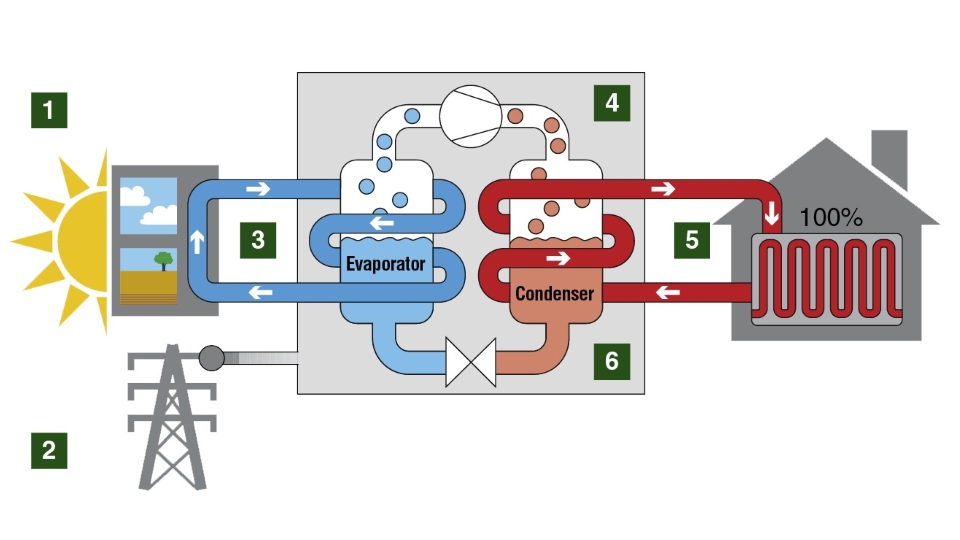
قبلاً در مجله فرادرس در مورد چرخه کارنو و قضیه کارنو بحث کردیم. اگر یخچال یا پمپ حرارتی براساس چرخه معکوس کارنو عمل کنند، به ترتیب به آنها یخچال کارنو (Carnot Refrigerator) یا پمپ حرارتی کارنو (Carnot Heat Pump) گفته می‌شود. به دلیل تشابه عملکرد این دو دستگاه ترمودینامیکی، در این مقاله، همزمان با یخچال کارنو پمپ حرارتی را نیز بررسی خواهیم کرد.

ضریب عملکرد یخچال کارنو و پمپ حرارتی کارنو

ضریب عملکرد یخچال و پمپ حرارتی، صرف نظر از اینکه برگشت‌پذیر یا برگشت‌ناپذیر باشند، به صورت زیر تعیین می‌شود.

$$\large \text {COP} _ {\text {R}} \:=\: \frac {1} {Q_H/Q_L \:-\: 1} \\~\\ \large \text {COP} _ {\text {HP}} \:=\: \frac {1} {1\:-\: Q_L /Q_H}$$

فیلم آموزش ترمودینامیک 2 – مرور و تست کنکور ارشد در فرادرس

کلیک کنید

در رابطه‌های بالا، $$\large Q_L$$ مقدار گرمای جذب شده از منبع سرد است و مقدار گرمای آزاد شده در منبع گرم نیز با $$\large Q_H$$ نشان داده می‌شود. در فرمول محاسبه ضریب عملکرد تمام یخچال‌ها و پمپ‌های حرارتی برگشت‌پذیر، می‌توانیم در رابطه‌های بالا، نسبت انتقال حرارت را با نسبت دمای مطلق (دما برحسب کلوین) منبع گرم و سرد جایگزین کنیم. از این رو، ضریب عملکرد یخچال‌ها و پمپ‌های حرارتی برگشت‌پذیر به قرار زیر است.

$$\large \text {COP} _ {\text {R, rev}} \:=\: \frac {1} {T_H/T_L \:-\: 1} \\~\\ \large \text {COP} _ {\text {HP, rev}} \:=\: \frac {1} {1\:-\: T_L /T_H}$$

رابطه‌های بالا بیشترین ضریب عملکرد ممکن را برای یخچال‌ها و پمپ‌های حرارتی که بین دو دمای $$\large T_L$$ و $$\large T_H$$ کار می‌کنند، نشان می‌دهد. در عمل، تمام یخچال‌ها و پمپ‌های حرارتی واقعی که بین این دو دما کار می‌کنند، ضریب عملکرد پایین‌تری خواهند داشت.

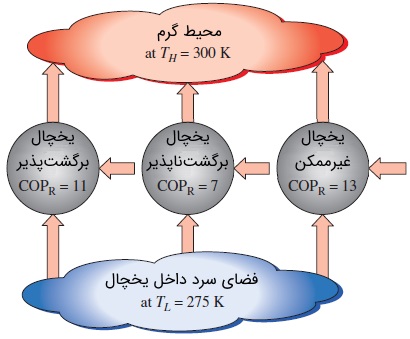
می‌توان بین یخچال‌های واقعی و برگشت‌پذیری که بین دو دمای یکسان کار می‌کنند، مقایسه‌ای انجام داد. اگر چرخه عملکرد یخچال، برگشت‌ناپذیر باشد (یخچال واقعی)، ضریب عملکرد آن از $$\large \text {COP} _ {\text {R, rev}}$$ کمتر است. اگر یخچال با چرخه برگشت‌پذیر کار کند، ضریب عملکرد آن با $$\large \text {COP} _ {\text {R, rev}}$$ برابر است. یخچالی که در این چرخه کار کند، یخچال کارنو نامیده می‌شود. همچنین امکان ندارد که ضریب عملکرد از $$\large \text {COP} _ {\text {R, rev}}$$ بزرگتر باشد و ساخت یخچالی با این ویژگی غیرممکن است. با قرار دادن $$\large \text {COP} _ {\text {HP, rev}}$$ به جای $$\large \text {COP} _ {\text {R, rev}}$$ می‌توان مقایسه مشابهی بین پمپ‌های حرارتی نیز انجام داد که نتایج آن به همین صورت خواهد بود.

ضریب عملکرد یک یخچال یا پمپ حرارتی برگشت‌پذیر، بیشترین مقداریست که می‌توان بین آن دو دمای مشخص شده، به آن دست یافت. در ساخت پمپ‌های حرارتی و یخچال کارنو می‌توان با اجرای طراحی‌های دقیق‌تر، به این اعداد نزدیک شد ولی رسیدن به آنها هرگز ممکن نخواهد بود. در پایان باید به این نکته اشاره کرد که ضریب عملکرد یخچال‌ها و پمپ‌های حرارتی با کاهش دمای $$\large T_L$$ پایین می‌آید. به عبارت دیگر، در این حالت، برای جذب حرارت از منبع سرد، به کار بیشتری نیاز است. به محض اینکه دمای فضای سرد به صفر برسد، میزان کار لازم برای انجام عمل تبرید، بینهایت شده و ضریب عملکرد $$\large \text {COP} _ {\text {R}}$$ به صفر می‌رسد.

مثال ۱: عملکرد چرخه یخچال کارنو در مخلوط اشباع

سؤال: در یک یخچال کارنو که در یک سیستم بسته و ناحیه مخلوط مایع -- بخار اشباع عمل می‌کند، مقدار $$\large 0.8\: \text {kg}$$ از مبردی با نام تجاری $$\large 134 \text {a}$$ به عنوان سیال عامل استفاده شده است. نمودار $$\large T-V$$ مربوط به این چرخه در شکل زیر نشان داده شده است. دماهای ماکزیمم و مینیمم در این چرخه به ترتیب برابر با $$\large 20\: ^\circ \text {C}$$

فیلم آموزش ترمودینامیک – حل سوالات کنکور ارشد و دکتری در فرادرس

کلیک کنید

می‌دانیم که در انتهای فرآیند آزاد شدن گرما، سیال مبرد در حالت مایع اشباع قرار دارد و کار خالص ورودی به چرخه برابر $$\large 15\: \text {kJ}$$ است. کسر جرمی مبرد که در خلال فرآیند دریافت گرما تبخیر می‌شود و همچنین فشار را در انتهای فرآیند آزاد شدن گرما تعیین کنید. آنتالپی تبخیر مبرد $$\large 134 \text {a}$$ در دمای $$\large -8\: ^\circ \text {C}$$

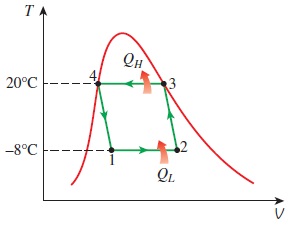
پاسخ: می‌دانیم عملکرد یخچال مطابق با چرخه ایده‌آل کارنو است. با داشتن دماهای بالا و پایین، ضریب عملکرد چرخه یخچال کارنو به صورت زیر محاسبه می‌شود.

$$\large \text {COP} _{\text {R}} \;=\: \frac {1} {T_H/ T_L \:-\: 1} \:=\: \frac {1} {(20 \:+\: 273\: \text {K})/ (-\:8 \:+\: 273\: \text {K}) \:-\:1} \:=\: 9.464$$

مقدار انرژی حرارتی مبادله شده با منبع سرد را می‌توانیم با کمک تعریف ضریب عملکرد و به صورت زیر به دست آوریم.

$$\large Q_L \:=\: \text {COP} _{\text {R}} \:\times\: W_ {\text {in}} \:=\: (9.464) (15\: \text {kJ}) \:=\: 142\: \text {kJ}$$

اکنون می‌توانیم بخشی از مبرد که در حین جذب گرما در یخچال کارنو بخار می‌شود را بیابیم.

$$\large Q_L \:=\: m_ {\text {evap}} h_{fg \:@ -8 \:^\circ \text {C}} \\~\\<br /> \large \Rightarrow ~~~ m_ {\text {evap}} \:=\: \frac {142\: \text {kJ}} {204.59\: \text {kJ}/ \text {kg}} \:=\: 0.694\: \text {kg}$$

بنابراین، کسر جرمی تبخیر شده در حین فرآیند دریافت گرما توسط مبرد، به شیوه زیر تعیین می‌شود.

$$\large \frac {m_ {\text {evap}}} {m_ {\text {total}}} \:=\: \frac {0.694\: \text {kg}} {0.8\: \text {kg}} \:=\: 0.868$$

در انتهای فرآیند آزاد شدن گرما، فشار برابر با فشار اشباع در آن دما است و مقدار آن از طریق جدول‌های ترمودینامیکی قابل دستیابی خواهد بود. در این مورد، این فشار برابر با مقدار زیر است.

$$\large P_4 \:=\: P_ {\text {sat @} \:20 ^\circ \text {C}} \:=\: 572.1\: \text {kPa}$$

چرخه یخچال کارنو یک چرخه ایده‌آل است و در واقعیت، اجرای چنین چرخه‌ای غیرممکن است.

مثال ۲: گرمایش خانه با کمک پمپ حرارتی کارنو

سؤال: در فصل زمستان، از یک پمپ حرارتی برای گرمایش خانه استفاده شده است. شکل زیر را مشاهده کنید. دمای هوای داخل خانه باید در عدد $$\large 21\: ^\circ \text {C}$$

فیلم آموزش ترمودینامیک پیشرفته – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

هنگامی که دمای هوای بیرون $$\large -5\: ^\circ \text {C}$$

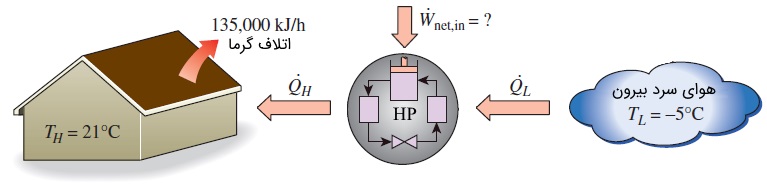
پاسخ: عملکرد پمپ حرارتی را پایدار فرض می‌کنیم. پمپ حرارتی فقط در شرایطی می‌تواند با مینیمم توان کار کند، که عملکرد آن مطابق با چرخه کارنو باشد. در نتیجه، با یک پمپ حرارتی برگشت‌پذیر روبرو هستیم. ضریب عملکرد مربوط به پمپ حرارتی برگشت‌پذیری که بین هوای خانه و بیرون قرار دارد، به صورت زیر قابل محاسبه است.

$$\large \text {COP}_ {\text {HP} ,\: \text {rev}} \:=\: \frac {1} {1\:-\: T_L/ T_H} \:=\: \frac {1} {1\:-\: (-\:5 \:+\: 273\: \text {K}) /(21 \:+\: 273\: \text {K})} \:=\: 11.3$$

سپس توان مورد نیاز ورودی برای عملکرد این پمپ حرارتی برگشت‌پذیر به دست می‌آید.

$$\large \dot {W} _{\text {net, in}} \:=\: \frac {\dot {Q} _{\text {H}}} {\text {COP}_ {\text {HP}}} \:=\: \frac {37.5\: \text {kW}} {11.3} \:=\: 3.32\: \text {kW}$$

این پمپ حرارتی برگشت‌پذیر قادر است گرمایش خانه را با مصرف تنها $$\large 3.32\: \text {kW}$$ توان الکتریکی تأمین کند. اگر قرار باشد همین خانه با استفاده از هیترهای مقاومت الکتریکی گرم شود، مصرف توان الکتریسیته با افزایش $$\large 11.3$$ برابری به عدد $$\large 37.5\: \text {kW}$$ خواهد رسید. زیرا در هیترهای مقاومتی، انرژی الکتریکی به نسبت یک به یک به گرما تبدیل می‌شوند. اما در پمپ حرارتی، انرژی از فضای بیرون جذب شده و در فضای اتاق آزاد می‌شود. مهم‌تر اینکه، سیال کاری به کار گرفته شده در این چرخه تبرید، تنها به $$\large 3.32\: \text {kW}$$ توان الکتریکی نیاز دارد. توجه کنید که پمپ حرارتی انرژی را تولید نمی‌کند و تنها آن را از محیطی (محیط سرد) به محیطی دیگر (محیط گرم) انتقال می‌دهد. در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• ترمودینامیک — از صفر تا صد
• قانون دوم ترمودینامیک – از صفر تا صد
• فرآیند احتراق یا سوختن — از صفر تا صد
• تعریف گرما و دما در ترمودینامیک — به زبان ساده

^^