چرخ دنده مارپیچ – از صفر تا صد

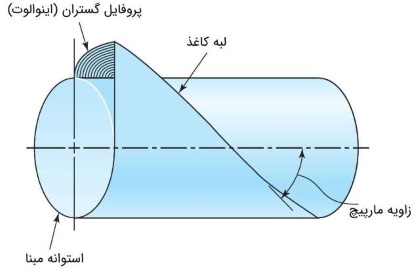
در مقاله چرخ دنده - به زبان ساده، انواع چرخ دنده را معرفی کردیم. چرخ دنده مارپیچ (Helical Gear) بیشتر برای انتقال حرکت بین محورهای موازی به کار می‌رود. زاویه مارپیچ در هر دو چرخ دنده درگیر، یکسان است. ولی یکی از آنها باید راست‌گرد و دیگری چپ‌گرد نصب شوند. دندانه این چرخ دنده به شکل یک هلیکوئید گستران (Involute Helicoid) است. به تصویر زیر دقت کنید. کاغذی را که به شکل یک متوازی‌الاضلاع بریده شده به دور یک استوانه بپیچید. در این حالت، لبه مورب کاغذ، یک مارپیچ را تشکیل می‌دهد. حال کاغذ را به آرامی از دور استوانه باز می‌کنیم. هر نقطه روی لبه مورب کاغذ، یک منحنی گستران ایجاد می‌کند. اکنون اگر همه این منحنی‌های گستران را کنار هم قرار دهیم، یک صفحه تشکیل می‌شود. به این صفحه، هلیکوئید گستران گفته می‌شود.

تماس اولیه دندانه در چرخ دنده ساده، خطی است که در تمام طول مسیر روی سطح دندانه گسترش پیدا می‌کند. اما در چرخ دنده مارپیچ، تماس اولیه، نقطه‌ایست که همزمان با درگیری بیشتر دندانه، به صورت یک خط گسترش می‌یابد. در چرخ دنده ساده، خط تماس، موازی محور چرخش است. در چرخ دنده‌های مارپیچ، این خط نسبت به سطح دندانه، مورب است. همین درگیری آرام‌آرام و انتقال یکنواخت بار از یک دندانه به دندانه دیگر، این قابلیت را به چرخ دنده مارپیچ می‌دهد تا در سرعت‌های بالا، بارهای سنگینی را انتقال دهد. به دلیل ماهیت تماس بین چرخ دنده‌های مارپیچ، نسبت تماس اهمیت زیادی ندارد. در اینجا ناحیه تماس مهم است. ناحیه تماس، تا حد زیادی به عرض سطح چرخ دنده بستگی دارد.

چرخ دنده مارپیچ برای نسبت‌های سرعت $$3:2$$ تا $$10:1$$ به کار می‌رود و دارای راندمانی در حدود $$94$$ تا $$98$$ درصد است. کاربرد چرخ دنده‌های مارپیچ مانند چرخ دنده‌های ساده است. با این تفاوت که دیگر محورها لزوماً موازی نیستند. علاوه بر آن، این نوع چرخ دنده‌ها انتقال قدرت را بسیار نرم‌تر و با صدای کمتری نسبت به چرخ دنده‌های ساده، انجام می‌دهند.

چرخ دنده مارپیچ دوبل

چرخ دنده‌های مارپیچ، نیروی شعاعی و تراست را به یاتاقان‌های محور وارد می‌کنند. هنگامی که نیروی تراست خیلی زیاد شود، استفاده از چرخ دنده مارپیچ دوبل توصیه می‌شود. نام دیگر این چرخ دنده‌ها، جناغی است. در این حالت و در هریک از چرخ دنده‌های مارپیچ، نیروی تراست خلاف جهت دیگری است. در نتیجه نیروی تراست خود به خود خنثی می‌شود. لوگوی شرکت خودروسازی سیتروئن فرانسه، به پاس تلاش‌های «آندره سیتروئن» (Andre Citroen) در طراحی چرخ دنده‌های جناغی، برگرفته از این نوع چرخ دنده است.

نمونه‌ای از چرخ دنده‌های جناغی را در شکل زیر مشاهده می‌کنید. هنگامی که دو یا چند چرخ دنده مارپیچ روی یک محور نصب می‌شوند، جهت گردش آنها (راست‌گرد یا چپ‌گرد بودن) باید طوری تعیین شود که نیروی تراست به حداقل برسد.

پارامترهای هندسی چرخ دنده مارپیچ

شکل زیر بخشی از نمای یک چرخ دنده مارپیچ را نشان می‌دهد. خطوط $$ab$$ و $$cd$$ از مرکز دو دندانه مجاور عبور می‌کنند و در یک صفحه گام هستند. زاویه مارپیچ را با $$\large \psi$$ نشان داده‌ایم. فاصله بین دو سرِ خط $$ac$$، گام دایره‌ای عرضی نامیده شده و با $$\large p_t$$ نشان داده می‌شود. پارامتر بعدی، گام عمودی $$\large p_n$$ است که فاصله $$ae$$ را شامل می‌شود. این دو پارامتر را می‌توان با استفاده از رابطه زیر به هم تبدیل کرد.

$$\large p_n = p_t \:\cos \psi$$

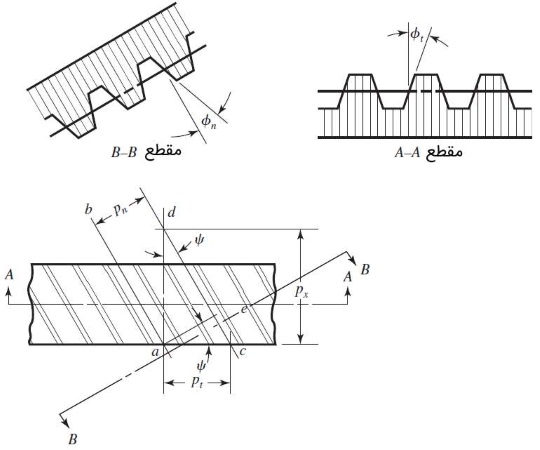
گام محوری، با $$\large p_x$$ نشان داده می‌شود. برای محاسبه گام محوری می‌توان به طریق زیر عمل کرد.

$$\large p_x = \frac {p_t}{\tan \:\psi}$$

قبلاً و در مقاله‌ای مربوط به چرخ دنده‌های ساده، رابطه زیر را بین گام قطری و گام دایره‌ای تعریف کردیم.

$$\large p_n P_n = \pi$$

حال می‌توان رابطه‌ای بین گام قطری عمودی و گام قطری عرضی به صورت زیر پیدا کرد.

$$\large p_n = \frac {p_t}{\cos \psi}$$

زاویه فشار در جهت عمودی $$\large \phi _ n$$ است و با زاویه فشار در جهت چرخش $$\large \phi _ t$$ متفاوت است. دلیل این موضوع هم، زاویه‌دار بودن دندانه‌هاست. این دو زاویه فشار را می‌توان با کمک رابطه زیر به یکدیگر تبدیل کرد.

$$\large \cos \psi = \frac {\tan \phi _n}{\tan \phi _t}$$

شکل زیر، برش استوانه‌ای ایجاد شده توسط صفحه مورب $$ab$$ را با زاویه $$\large \psi$$ نشان می‌دهد. این صفحه مورب، کمانی به شعاع $$\large R$$ جدا کرده است. برای وضعیتی که $$\large \psi = 0$$ باشد، شعاع کمان برابر $$\large R = \frac {D}{2}$$ است. اگر فرض کنیم زاویه $$\large \psi$$ آرام آرام و به تدریج از صفر به $$90$$ درجه برسد، مقدار $$\large R$$ از $$\large \frac {D}{2}$$ شروع شده و به $$\large R = \infty$$ میل خواهد کرد.

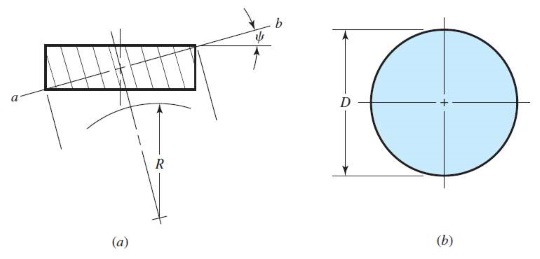
اگر در جهت دندانه‌ها نگاه کنیم، شعاع گام برای چرخ دنده مارپیچ، برابر با $$\large R$$ به نظر خواهد رسید. چرخ دنده با گام مشابه و شعاع $$\large R$$ تعداد دندانه بیشتری خواهد داشت. زیرا شعاع آن افزایش یافته است. در مورد چرخ دنده مارپیچ، این عدد به عنوان تعداد مجازی دندانه‌ها تعریف می‌شود. از طریق رابطه‌های هندسی می‌توان فرمول زیر را برای محاسبه تعداد مجازی دندانه‌ها در چرخ دنده مارپیچ ارائه کرد.

$$\large N^\prime= \frac {N}{\cos^3\psi}$$

در رابطه بالا تعداد واقعی دندانه‌ها با $$\large N$$ و تعداد مجازی آنها با $$\large N^\prime$$ نشان داده شده است. در مرحله طراحی، دانستن تعداد مجازی دندانه‌ها برای مقاومت و برش مارپیچ دندانه‌ها ضروری است.

دندانه‌های چرخ دنده مارپیچ هم می‌تواند مانند چرخ دنده ساده تداخل داشته باشد. تداخل، به درگیری بخشی از منحنی‌های چرخ دنده گفته می‌شود که باهم مزدوج نیستند. پیش‌تر، رابطه‌ای برای ارتباط بین زاویه‌های فشار در جهت عمودی و چرخش (مماسی) تعریف کردیم. حال می‌توانیم زاویه فشار در جهت مماسی را به صورت زیر بیابیم.

$$\large \phi_t=\tan^{-1}(\frac {\tan\phi_n}{\cos\psi})$$

کمترین تعداد دندانه $$\large N_P$$ در یک پینیون مارپیچ - ساده که بتواند بدون تداخل با چرخ دنده‌ای با تعداد دندانه یکسان درگیر شود، با رابطه زیر محاسبه می‌شود.

$$\large N_P=\frac {2k\cos\psi}{3\sin^2\phi_t}(1+\sqrt{1+3\sin^2\phi_t})$$

به عنوان مثال، اگر زاویه فشار عمودی $$\large \phi_n$$ برابر با $$\large 20^\circ$$ و زاویه مارپیچ $$\large \psi$$ برابر با $$\large 30^\circ$$ باشد، رابطه زیر برقرار می‌شود.

$$\large \phi_t=\tan^{-1}(\frac {\tan \:20^\circ}{\cos \:30^\circ}) = 22.8^\circ\\~\\ \large N_P=\frac {2(1) \cos 30 ^\circ}{3 sin^2\:22.8^\circ}(1+\sqrt{1+3\:sin^2\: 22.8^\circ}) = 8.48 = 9$$

اگر نسبت چرخ دنده را $$\large m_G = \frac {N_G}{N_P} = m$$ فرض کنیم، کمترین تعداد دندانه با کمک رابطه زیر به دست می‌آید.

$$\large N_P = \frac {2k\:\cos \psi}{(1+2m) sin^2\phi_t}[m+\sqrt{m^2 + (1+2m)sin^2\phi_t}]$$

بزرگترین چرخ دنده‌ای که بتواند با چنین پینیونی درگیر شود، مطابق رابطه زیر قابل محاسبه است.

$$\large N_G=\frac {N^2_P \:\sin^2\phi_t-4k^2 \:\cos^2\psi}{4k \:\cos\psi\:-2\:N_P\sin^2\phi_t}$$

به عنوان مثال، برای پینیونی با ۹ دندانه، زاویه فشار $$\large \phi_n$$ برابر $$\large 20^ \circ$$، زاویه مارپیچ $$\large \psi$$ برابر $$\large 30^ \circ$$ و همچنین زاویه فشار مماسی $$\large \phi_t$$ برابر $$\large 22.8^ \circ$$، تعداد دندانه‌های چرخ دنده به صورت زیر خواهد بود.

$$\large N_G=\frac {9^2 \sin^222.8^ \circ -4(1)^2\cos^230^ \circ}{4(1)\cos30^ \circ - 2(9) \:sin^2 22.8^\circ} = 12.02 = 12$$

مثال ۱

سؤال: در یک چرخ دنده مارپیچ، زاویه فشار عمودی $$\large 20^\circ$$، زاویه مارپیچ $$\large 25^\circ$$ و گام قطری عرضی برابر $$\large 6\:teeth/in$$ است. اگر تعداد دندانه‌ها $$\large 18$$ باشد، الف) قطر دایره گام، ب) گام‌های عرضی، عمودی و محوری، پ) گام قطری عمودی و ت) زاویه فشار عرضی را محاسبه کنید.

پاسخ: الف) قطر دایره گام به راحتی و به صورت زیر به دست می‌آید.

$$\large d=\frac {N}{P_t}= \frac {18}{6} = 3\:in$$

ب) حال برای یافتن گام‌های عرضی، عمودی و محوری به طریق زیر عمل می‌کنیم.

$$\large p_t = \frac {\pi}{P_t} = \frac {\pi}{6} =0.5236\:in\\~\\ \large p_n=p_t\times\cos\psi = 05236 \times\cos25^\circ = 04745\:in\\~\\ \large p_x = \frac {p_t}{\tan \psi}= \frac {0.5236}{\tan 25^\circ}=1.123\:in$$

پ) اکنون با داشتن گام قطری عرضی و زاویه مارپیچ، گام قطری عمودی را به دست می‌آوریم.

$$\large p_n = \frac {p_t}{\cos\:\psi} = \frac {6}{\cos\:25^\circ} = 6.62$$

ت) در نهایت زاویه فشار عرضی را می‌توانیم به سادگی پیدا کنیم.

$$\large \phi_t = \tan^{-1}(\frac {\tan\phi_n}{\cos\psi}) = \tan^{-1}(\frac {\tan 20^\circ}{\cos 25^\circ}) = 21.88^\circ$$

محاسبه نیروها در چرخ دنده مارپیچ

شکل زیر، نمایی سه‌بعدی از نیروهای وارد به دندانه چرخ دنده مارپیچ را نشان می‌دهد.

نیروها در صفحه گام و به مرکز سطح دنده وارد شده‌اند. با استفاده از هندسه شکل، سه مؤلفه اصلی نیروی $$\large W$$ به صورت زیر محاسبه می‌شوند.

$$\large \begin{cases} W_r = W \:\sin\phi_n \\ W_t = W\: \cos\phi_n\:\cos\:\psi \\ W_a = W\: \cos\phi_n\: \sin\psi \end{cases}$$

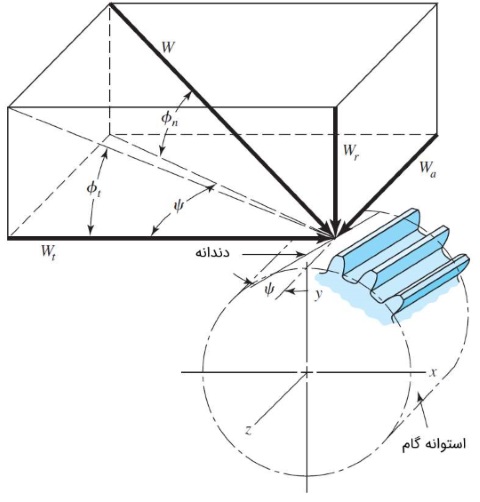
در رابطه‌های بالا، $$\large W_r$$ مؤلفه شعاعی است. مؤلفه مماسی با $$\large W_t$$ نمایش داده شده و نیروی انتقالی هم نامیده می‌شود. $$\large W_a$$ هم نیروی محوری یا همان نیروی تراست است.

معمولاً در مسئله‌های مختلف، مقدار $$\large W_r$$ داده می‌شود و باید بقیه مؤلفه‌ها را حساب کرد. بدین منظور از رابطه‌های زیر استفاده می‌کنیم.

$$\large W_r = W_t \:\tan\phi_t\\~\\ \large W_a = W_t \;\tan \psi\\~\\ \large W = \frac {W_t}{\cos\phi_n \:\cos \:\psi}$$

مثال 2

سؤال: شکل زیر، یک موتور الکتریکی را نشان می‌دهد که توان $$1$$ اسب بخار را در سرعت $$1800\:rev/min$$ انتقال می‌دهد. اگر از سمت جهت مثبت محور $$x$$ نگاه کنیم، این انتقال را در جهت حرکت عقربه‌های ساعت می‌بینیم. چرخ دنده پینیون از نوع مارپیچ و با $$\large 18$$ دندانه، به محور موتور الکتریکی متصل شده است. زاویه فشار، $$\large 20^\circ$$ و زاویه مارپیچ، $$\large 30^\circ$$ است. گام قطری را برابر با $$\large 12$$ دندانه در هر اینچ فرض کنید. جهت چرخش مارپیچ در شکل نشان داده شده است. با رسم نمودار سه‌بعدی پینیون و محور موتور، نیروهای وارد به پینیون و نیروهای عکس‌العمل یاتاقان‌های $$A$$ و $$B$$ را رسم و محاسبه کنید. نیروی تراست باید در نقطه $$A$$ دفع شود.

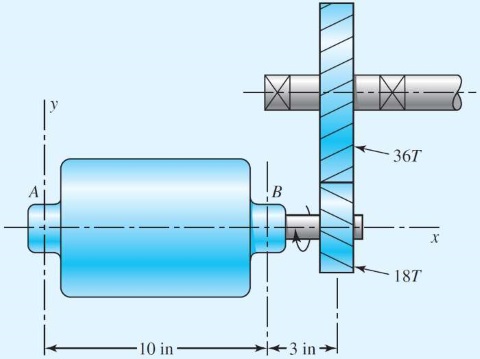
پاسخ: ابتدا زاویه فشار را در جهت مماسی (چرخشی) محاسبه می‌کنیم.

$$\large \phi_t=\tan^{-1} \frac {\tan \phi_n}{\cos\psi} = \tan^{-1}\frac {\tan\:20^\circ}{\cos\:30^ \circ} = 22.8^ \circ$$

همچنین می‌دانیم گام عرضی به صورت زیر و برحسب تعداد دندانه در هر اینچ، به دست می‌آید.

$$\large P_t = P_n\:\cos\psi = 12 \times\cos\:30^ \circ = 10.39$$

بنابراین، قطر گام در پینیون برابر با $$\large d_p = \frac {18}{10.39} = 1.732\:in$$ خواهد بود. حال سرعت خطی و نیروی انتقالی مماسی را با کمک روابط زیر پیدا می‌کنیم.

$$\large V=\frac {\pi dn}{12}= \frac {\pi (1.732)(1800)}{12} = 816 ft/min\\~\\ \large W_t = \frac {33,000 \times H}{V} = \frac {33,000 \times 1}{816} = 40.4\:lbf$$

برای محاسبه مؤلفه‌های دیگر نیرو، به طریق زیر عمل می‌کنیم.

$$\large W_r = W_t\tan\phi_t = (40.4)\tan22.8^ \circ = 17\: lbf\\~\\ \large W_a = W_t\tan\psi = (40.4)\tan 30^ \circ = 23.3\:lbf\\~\\ \large W = \frac {W_t}{\cos \phi_n\cos\psi} = \frac {40.4}{\cos 20^ \circ \cos30^ \circ} = 49.6\:lbf$$

به شکل پایین توجه کنید. نیروی $$\large W_r = 17\:lbf$$ در جهت منفی محور $$\large y$$ وارد می‌شود. نیروی $$\large W_a = 23.3\:lbf$$ در جهت منفی محور $$\large x$$ قرار دارد. راستای نیروی $$\large W_t = 40.4\:lbf$$ با جهت مثبت محور $$\large z$$ هم‌سو است. هر سه نیرو به نقطه $$\large C$$ وارد می‌شوند. عکس‌العمل یاتاقان را در نقطه‌های $$\large A$$ و $$\large B$$ فرض کرده‌ایم. مجموع گشتاور را حول محور $$\large z$$ می‌نویسیم.

$$\large F^x_A = W_a = 23.3\:lbf\\~\\ \large -(17)(13) + (23.3)(0.866) + 10\times F^y_B = 0\\~\\ \large F^y_B = 20.1\:lbf$$

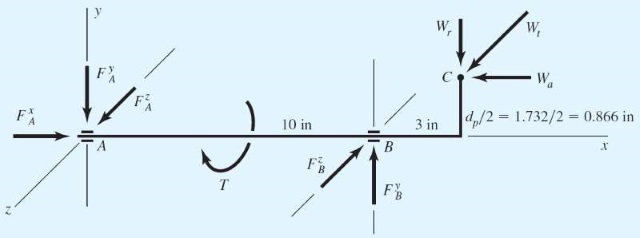
حال برآیند نیروها در جهت محور $$\large y$$ و $$\large z$$ و سپس مجموع گشتاورها را حول محور $$\large y$$ می‌نویسیم.

$$\large \sum_{}^{}F_y =0~~~\Rightarrow~~~F^y_A = 3.1\:lbf\\~\\ \large 10 \times F^z_B - (40.4)(13) = 0\\~\\ \large \Rightarrow~~~F^z_B = 52.5\:lbf\\~\\ \large \sum_{}^{}F_z =0~~~\Rightarrow~~~F^z_A = 12.1\:lbf$$

اکنون، گشتاور نشان داده شده در شکل را با رابطه زیر به دست می‌آوریم.

$$\large T=\frac {W_td_p}{2} = \frac {40.4 \times 1.732}{2} = 35\:lbf.in$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• چرخ دنده – به زبان ساده
• نسبت چرخ دنده — به زبان ساده
• چرخ دنده ساده – از صفر تا صد
• حرکت دایره ای – به زبان ساده