نمودار چندک چندک (Q-Q plot) — به زبان ساده

نمودار چندک چندک یا Q-Q plot به منظور مقایسه دو توزیع به کار گرفته می‌شود. از چنین نمودارهایی حتی می‌توان مطابقت توزیع داده‌ها را با یک توزیع مشخص، مورد بررسی قرار داد. توسط نمودار چندک چندک یا Q-Q plot شکل توزیع‌ها مقایسه می‌شود و یک تصویر گرافیکی یا نمودار برای نمایش میزان مطابقت آن دو توزیع نشان داده می‌شود. چولگی، پارامتر مرکزی و پراکندگی در نحوه مقایسه دو توزیع مشکلی ایجاد نمی‌کنند و به راحتی می‌توان هم توزیع (Equal Distributed) بودن داده‌ها را دو گروه مقایسه کرد. در این نوشتار به معرفی نمودار چندک-چندک یا Q-Q plot‌ خواهیم پرداخت و نحوه ترسیم آن را در نرم‌افزارهای محاسبات آماری نظیر R فرا می‌گیریم.

از آنجایی که برای رسم این نمودار از مقدار تابع احتمال تجمعی و تابع احتمال تجمعی تجربی استفاده می‌شود، بهتر است مطالب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و توزیع تجمعی — به زبان ساده را مطالعه کنید. همچنین توزیع تجمعی  — به زبان ساده نیز به روشن‌تر شدن موضوع این نوشتار کمک می‌کند. البته خواندن مطلب تابع توزیع تجربی در آمار — به زبان ساده هم خالی از لطف نیست.

نمودار چندک چندک یا Q-Q plot

یکی از روش‌های ناپارامتری (Non-parametric Method) در آمار، به منظور مقایسه یا برازش داده به یک توزیع، استفاده از رسم نمودار چندک-چندک یا Q-Q plot‌ است. در این شیوه، با استفاده از مقایسه شکل دو توزیع، می‌توان از لحاظ تصویری به یکسان بودن پارامترهای دو توزیع مانند، پارامتر مرکزی (Location Parameter)، پارامتر مقیاس (Scale Parameter) و همچنین پارامتر تقارن مانند چولگی (Skewness) پرداخت. از طرفی می‌توان، توزیع احتمالی داده‌ها را با یک توزیع دلخواه نیز مورد بررسی قرار داده و نتیجه بگیریم که آیا داده‌ها از توزیع خاصی پیروی می‌کنند یا خیر؟

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

در حقیقت روش تحلیل نمودار چندک-چندک یا Q-Q plot، تعمیم یافته روش مقایسه جدول فراوانی (Frequency Table) برای دو مجموعه داده است. برای مثال فرض کنید طبقه‌ها یا رده‌ها را برای دو مجموعه داده، به شکل یکسان ایجاد می‌کنیم. اگر مقادیر ستون فراوانی، یا فراوانی نسبی در هر دو جدول به هم نزدیک باشد، می‌توان نتیجه گرفت که داده‌ها دارای توزیع یکسان یا مشترکی هستند. البته این کار را به کمک ستون فراوانی نسبی تجعمی که همان تفسیر تابع توزیع تجمعی احتمال هست، نیز می‌توان انجام داد. این کار در حقیقت می‌تواند نموداری به نام P-P plot را ایجاد کند که البته نسبت به نمودار Q-Q plot کمتر به کار می‌رود.

نکته: نوع دیگری نیز از نمودار چندک چندک وجود دارد که کمتر از آن استفاده می‌شود. اگر به جای چندک‌های (مثلا صدک‌) توزیع و داده‌ها، فراوانی نسبی تجمعی و تابع احتمال تجمعی را ترسیم کنیم، نمودار حاصل را نمودار احتمال-احتمال یا P-P plot‌ می‌گویند.

مشابه آنچه در روش‌های آزمون نیکویی برازش (Goodness of Fit test) گفته شد، نمودار چندک-چندک یا Q-Q plot یک تکنیک تصویری محسوب می‌شود و احتیاجی به آگاهی از آماره آزمون و مقایسه مقدار آماره با توزیع آماره آزمون ندارد هر چند که برای نتیجه‌گیری از روش تحلیل چندک-چندک یا Q-Q plot احتیاج به اطلاعات دیگری در مورد توزیع‌ها یا میزان پراکندگی داده‌ها داریم.

روش‌های محاسبه چندک‌ها در نمودار Q-Q plot

محاسبه چندک‌ها براساس توزیع تجربی، بستگی به حوزه کاری و هدف از محاسبه این شاخص‌ها دارد. یکی از روش‌ها برای محاسبه چندک‌ها، استفاده از نسبت $$\frac{k}{n}$$‌ است که در آن $$k=1, 2, \ldots,n$$ بوده و این نسبت مقدار چندک نمونه‌ای را محاسبه می‌کند. به این ترتیب کافی است که داده‌ها را مرتب کرده و مقدار محاسبه شده در رابطه قبلی را به ترتیب به هر یک از مشاهدات مرتب شده نسبت دهیم. واضح است که بزرگترین مقدار همان چندک آخر یا صدک ۱۰۰ام خواهد بود و کوچکترین هم چندک اول یا صدک اول را تشکیل می‌دهد.

نکته: چندک‌ها براساس میزان احتمال محاسبه می‌شوند. بنابراین چندک 0.156 یعنی مقداری که احتمال تا آن نقطه برابر با 0.156 است. یعنی می‌توان نوشت:

$$\large P(X\leq q_{0.156})=0.156$$

به این ترتیب مشخص است که چندک با صدک تفاوت دارد زیرا احتمالات برای صدک‌ها مضرب‌هایی از 0.1 هستند مثلا اگر صدک سوم را با $$q_{0.3}$$ نشان دهیم، داریم:

$$\large P(X\leq q_{0.3})=0.3$$

به همین دلیل، این نمودار را با نام چندک-چندک یا Q-Q plot‌ می‌شناسند.

برای پیدا کردن مقدار $$q$$ شیوه‌های مختلف وجود دارد. ممکن است براساس اصلاح پیوستگی رابطه زیر برای محاسبه چندک‌ها به کار رود.

$$\large q=\dfrac{k-0.5}{n}$$

همچنین گاهی از رابطه دیگری برای تعیین و محاسبه مقدار احتمال تجمعی تجربی کمک گرفته می‌شود.

$$\large q=\dfrac{k}{n+1}$$

البته همه این محاسبات بستگی به جایگاه بزرگترین مقدار جامعه (Max) دارد که باید توسط نمونه تصادفی مورد برآورد قرار گیرد. برای کسب اطلاعات بیشتر در این زمینه می‌توانید مسئله تعداد تانک‌های آلمانی که توسط توزیع یکنواخت گسسته مورد بررسی قرار می‌‌گیرد را مطالعه کنید.

ساختار نمودار چندک چندک

نمودار چندک چندک یا Q-Q plot را که گاهی Quantile-Quantile plot‌ نیز می‌نامند، می‌توان براساس چندک‌های دو توزیع ترسیم کرد. در محور افقی چندک‌های توزیع اول و در محور عمودی نیز چندک‌های متناظر برای توزیع دوم مشخص می‌شود. اگر این مقادیر را در یک صفحه مختصات دکارتی ترسیم کنیم، یک نمودار چندک چندک یا Q-Q plot ایجاد کرده‌ایم.

اگر یک یا هر دو دسته مقادیر محور افقی یا عمودی دارای تابع توزیع تجمعی (CDF) پیوسته باشند، می‌توان مقادیر چندک‌ها را به صورت مجزا و منحصر به فرد محاسبه و ترسیم کرد. این کار با معکوس کردن تابع احتمال توزیع تجمعی صورت می‌گیرد.

$$\large q_p=F^{-1}(p)$$

رابطه ۱

در رابطه ۱، منظور از $$p$$ درصد مربوط به چندک است. همچنین $$F$$ نیز تابع احتمال تجمعی و $$F^{-1}$$ معکوس تابع احتمال تجمعی را مشخص می‌کند. طرف چپ رابطه، همان چندک مرتبه $$p\times 100$$ خواهد بود.

فرض کنید لازم است که صدک پنجم یک توزیع مشخص شود. برای این کار کافی است $$p=0.05$$ باشد. آنگاه به دنبال نقطه‌ای در توزیع می‌گردیم که احتمال تا آنجا برابر با $$0.05$$‌ باشد. این نقطه همان صدک پنجم ($$0.05\times 100=5$$) خواهد بود.

همچنین ممکن است که مقدار چندک‌های یک توزیع را براساس داده‌های یک نمونه تصادفی برآورد کرده باشیم. در این حالت برای نمایش اینکه داده‌ها از توزیع مورد نظر پیروی می‌کنند می‌توان به همان شکل چندک‌ها، را در محور افقی و عمودی مرتب کرده و نقاط مربوط به زوج‌های مرتب را در صفحه مختصات دکارتی مشخص کرد.

مثلا توزیع نرمال استاندارد را در نظر بگیرید. می‌خواهیم چندک یا در حقیقت صدک اول، تا نود و نهم را محاسبه کنیم. کدی که به زبان R نوشته شده است، در این کار به کمک ما می‌آید.

1qnorm(seq(0.01,0.99,0.01))

می‌دانیم که صدک پنجاهم همان میانه یا میانگین در توزیع نرمال است. از طرفی می‌دانیم که مقدار میانگین در این توزیع برابر با صفر است. پس صدک پنجاهم برابر با صفر خواهد بود. همچنین صدک ۹۵ هم برابر با 1.64 است و به علت تقارن، صدک ۵ام نیز برابر با 1.64- خواهد بود. به این ترتیب لیستی از صدک‌های توزیع نرمال تولید می‌شود.

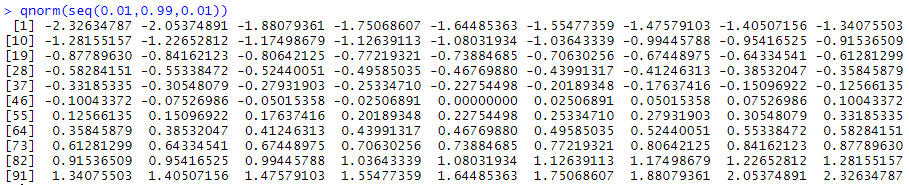
این داده‌های مربوط به محور افقی نمودار Q-Q plot خواهند بود. حال مقادیر مربوط به محور عمودی را مشخص می‌کنیم.

برای ایجاد داده‌های محور عمودی،  دویست مشاهده از توزیع نرمال استاندارد را به صورت تصادفی تولید کرده و صدک‌های این داده‌ها را محاسبه می‌کنیم. به این ترتیب به شکلی توزیع تجربی داده‌ها بدست خواهد آمد. کد زیر به منظور ایجاد این داده‌ها و محاسبه صدک‌های اول تا نود و نهم نوشته شده است.

1quantile(rnorm(200),probs = seq(0.01,0.99,0.01))

بنابراین می‌بینیم که اعداد و ارقام حاصل توسط تابع quantile در اصل فقط داده‌های شما هستند که به ترتیب صعودی مرتب شده‌اند. با این وجود شایان ذکر است که روش‌های بسیاری برای محاسبه چندک‌ها یا صدک‌ها وجود دارد. برای ترسیم نمودار Q-Q plot، داده‌های شما پس از مرتب‌سازی صعودی در مقابل مقادیر محاسبه شده چندک‌ها از یک توزیع آماری ترسیم می‌شوند. بنابراین از نمودار Q-Q plot‌ می‌توان برای مطابقت توزیع داده‌ها با هر توزیع آماری استفاده کرد.

حال کافی است که دو مجموعه داده که در قسمت قبل آماده شده‌اند را در مقابل یکدیگر توسط یک نمودار ترسیم کنیم. در حقیقت نمودار چندک- چندک، یک نمودار نقطه‌ای (Scatter plot) است که با دستور plot‌ در R قابل پیاده‌سازی است.

1x=qnorm(seq(0.01,0.99,0.01))
2y=quantile(rnorm(200),probs = seq(0.01,0.99,0.01))
3plot(x,y)

با اجرای کد بالا، نموداری شبیه تصویر زیر ساخته می‌شود.

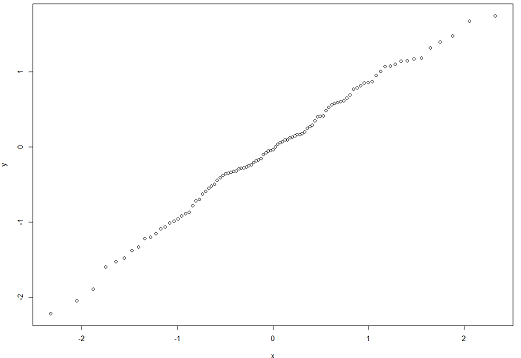
البته برای ترسیم چنین نموداری می‌توانید مستقیما از تابع qqnorm یا qqplot‌ در زبان برنامه‌نویسی و محاسبات آماری R استفاده کنید.

رسم نمودار چندک چندک با تابع qqnorm‌

تابع qqnorm یک نمودار چندک-چندک یا Q-Q plot برای مطابقت با توزیع نرمال ایجاد می‌کند به همین علت هم در انتهای نام آن عبارت norm را مشاهده می‌کنید. کافی است که یک بردار از مقادیر مشاهدات به این تابع معرفی کنید تا چندک‌های محاسبه شده براساس نمونه را با چندک‌های مربوط به توزیع نرمال مقایسه کند.

فیلم آموزش کاربرد اکسل Excel در مهندسی صنایع در فرادرس

کلیک کنید

به عنوان مثال، مجموعه داده درختان tree‌ در R را در نظر بگیرید. در این مجموعه داده، اندازه‌گیری درختچه شامل قد و حجم چوب در 31 درخت گیلاس سیاه قطعه قطعه شده ثبت شده است. یکی از متغیرهای این مجموعه داده، ارتفاع (Height) است. آیا می‌توانیم ادعا کنیم که متغیر ارتفاع درختچه‌ها در این نمونه تصادفی، دارای توزیع نرمال است؟

کدهای زیر به منظور نمایش چند سطر اول این داده‌ها و ترسیم نمودار چندک چندک یا Q-Q plot‌ نوشته شده‌اند.

1head(trees)
2qqnorm(trees$Height)

خروجی‌ها به صورت زیر هستند.

> head(trees)
Girth Height Volume
1 8.3 70 10.3
2 8.6 65 10.3
3 8.8 63 10.2
4 10.5 72 16.4
5 10.7 81 18.8
6 10.8 83 19.7

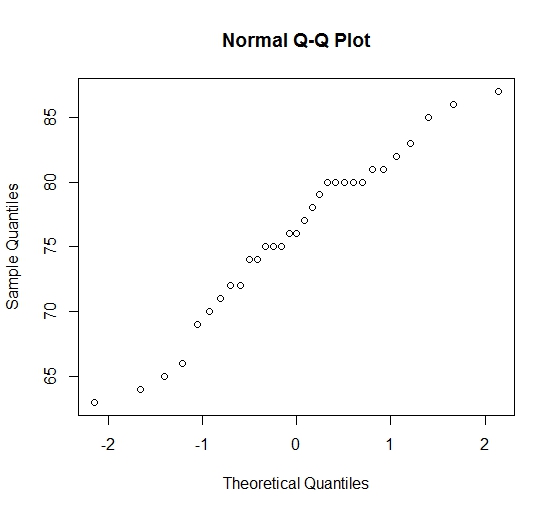
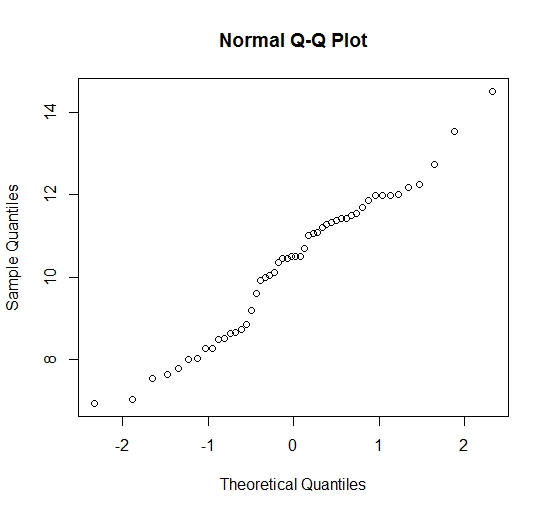
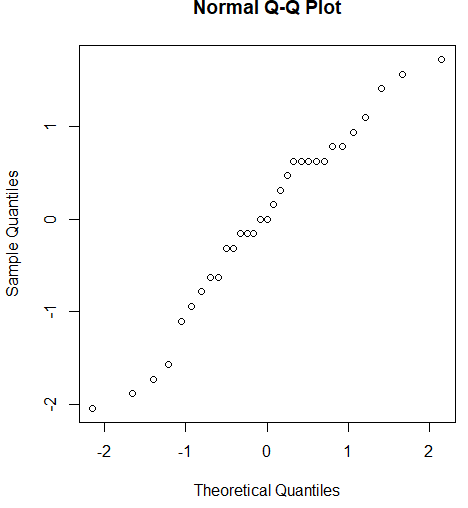
همانطور که دیده می‌شود، فرضیه نرمال بودن ارتفاع درختچه‌ها توسط این نمونه تصادفی مورد تایید قرار می‌گیرد زیرا تقریبا نمودار حاصل، خط راستی است که از مرکز مختصات گذر کرده است و به نظر نیمساز ربع اول مختصات دکارتی محسوب می‌شود.

توجه داشته باشید که محور افقی، مقادیر چندک‌ها براساس توزیع نرمال استاندارد (با میانگین صفر و واریانس ۱) بوده و مقادیر روی محور عمودی، چندک‌های داده‌ها براساس توزیع تجربی داده‌ها است که میانگین و واریانس متفاوتی با توزیع نرمال استاندارد دارند. به همین علت مقیاس روی محور افقی و عمودی با یکدیگر متفاوت است.

نکته: برای اینکه داده‌های نمونه تصادفی نیز دارای میانگین صفر و واریانس ۱ شوند می‌توانستیم با دستور scale، مقیاس اندازه‌گیری را برایشان از بین ببریم و سپس نمودار را ترسیم کنیم تا هر دو محور دارای مقیاس یکسانی باشند ولی در نهایت نمودار ترسیم شده در شکل ۳ در این حالت نیز درست به شکل نمودار ۲ بدست می‌آید.

1qqnorm(scale(trees$Height))

نمودار حاصل توسط دستور بالا فقط در محور عمودی تفاوت دارد که هم مقیاس با محور افقی است.

تفسیر نمودار چندک چندک با تابع qqplot

تابع qqplot به شما این امکان را می‌دهد که برای هر توزیع احتمالی نمودار چندک-چندک یا Q-Q plot را ترسیم کنید. برخلاف تابع qqnorm، برای این تابع باید دو پارامتر مشخص شود. هر دو این پارامترها یک مجموعه داده را نشان می‌دهند که باید چندک‌های آن‌ها با یکدیگر مقایسه شوند.

به عنوان یک مثال فرض کنید می‌خواهیم نمودار چندک چندک یا Q-Q plot را به منظور آزمون برازش مجموعه داده‌های randu با توزیع یکنواخت (Uniform Distribution) انجام دهیم. این مجموعه داده در قالب یک چارچوب داده (DataFrame) در زبان برنامه‌نویسی R موجود است و احتیاجی به بارگذاری (Load) آن نیست.

سه ستون یا متغیر و ۴۰۰ مشاهده در مجموعه randu وجود دارد. هر کدام از این ستون‌ها، مقادیر تصادفی از توزیع یکنواخت در بازه صفر و یک هستند. می‌خواهیم مشخص کنیم که متغیر اول یعنی $$x$$ دارای توزیع یکنواخت در بازه صفر و یک است یا خیر؟ با فرض اینکه توزیع متغیر $$V$$‌ نیز یکنواخت در همان بازه است در حقیقت می‌خواهیم هم توزیعی ستون اول را با $$V$$ نشان دهیم.

این سوال را با نماد ریاضی می‌توان به صورت به صورت $$x \stackrel{D}{=} V \sim U(0,1)$$ نشان داد.

به کمک کد زیر قسمتی از این مجموعه داده نمایش داده می‌شود.

1 head(randu)
2         x        y        z
31 0.000031 0.000183 0.000824
42 0.044495 0.155732 0.533939
53 0.822440 0.873416 0.838542
64 0.322291 0.648545 0.990648
75 0.393595 0.826873 0.418881
86 0.309097 0.926590 0.777664

مشخص است که مقادیر در بازه صفر تا یک برای هر سه ستون، تغییر می‌کند. ابتدا مقدار تابع توزیع تجربی را برای مقادیر متغیر $$x$$ به صورت زیر محاسبه می‌کنیم.

1ps=ppoints(length(randu$x)))

حال به کمک تابع quinf مقدار چندک‌ها را براساس احتمال توزیع یکنواخت برای هر یک از مقادیر احتمال که در قسمت قبل تهیه شده، بدست می‌آوریم.

1qs=qunif(ps)

در انتها نیز با تابع qqplot نمودار چندک-چندک یا Q-Q plot را برای چندک‌های حاصل از توزیع تجربی و چندک‌های توزیع یکنواخت متناظر با داده‌ها، ترسیم می‌کنیم.

1qqplot(randu$x,qs)

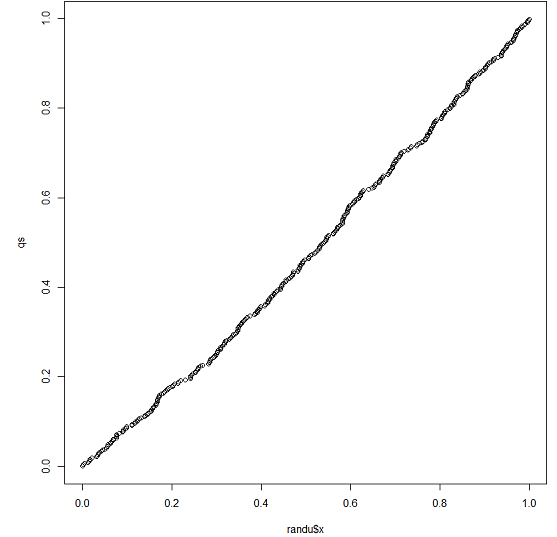
همانطور که دیده شد، تابع ppoints مقادیر احتمال یا احتمال فراوانی نسبی تجمعی را برای نقاط محاسبه کرد. سپس برای هر یک از این احتمال‌ها، نقاط چندک‌های توزیع یکنواخت توسط qunif بدست آمد. در انتها نیز این مقادیر با یکدیگر روی نمودار qqplot ترسیم شدند.

از آنجایی که نمودار ترسیم شده کاملا شبیه نیمساز ربع اول مختصات دکارتی است شواهد مناسبی وجود دارد که متغیر یا ستون $$x$$‌ از مجموعه داده randu دارای توزیع یکنواخت در بازه صفر و یک است.

نمایش عدم هم‌توزیعی توسط نمودار چندک چندک

همانطور که توسط نمودار Q-Q plot، هم‌توزیعی را نشان دادیم، عدم هم‌توزیعی را هم می‌توان توسط این نمودار نتیجه گرفت. برای این که نحوه نمایش چنین حالتی در نمودار Q-Q plot بهتر دیده شود، مثال‌هایی در این مورد می‌زنیم.

فیلم آموزش مفاهیم آماری در داده کاوی و پیاده سازی آن در پایتون Python در فرادرس

کلیک کنید

فرض کنید دو ستون داده تولید کرده‌ایم که اولی از توزیع نرمال (Normal Distribution) و دومی از توزیع کای ۲ (Chi Square Distribution) با سه درجه آزادی است. می‌خواهیم نمودار Q-Q plot را برای مقایسه یا هم‌توزیع بودن آن‌ها ترسیم کنیم. در کد زیر ۳۰ مشاهده از هر یک از این توزیع‌ها تولید کرده و چارک‌ها را محاسبه و در مقابل یکدیگر ترسیم کرده‌ایم.

1qqplot(qnorm(ppoints(30)), qchisq(ppoints(30),df=3))

نتیجه نموداری شبیه تصویر زیر خواهد بود.

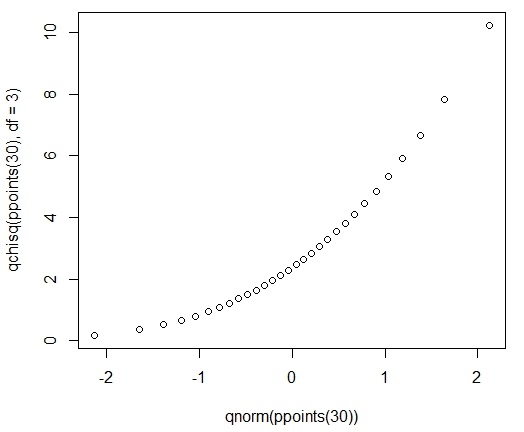
به خوبی در تصویر بالا دیده می‌شود که نمودار نقاط، شبیه نیمساز ربع اول مختصات دکارتی نیست بلکه شبیه یک محنی درجه ۲ شده است. به نظر می‌رسد که مقادیر متغیر تصادفی توزیع کای ۲ در چندک‌هایی پایینی کوچکتر از توزیع نرمال و در چندک‌هایی بالایی، بزرگتر از توزیع نرمال هستند.

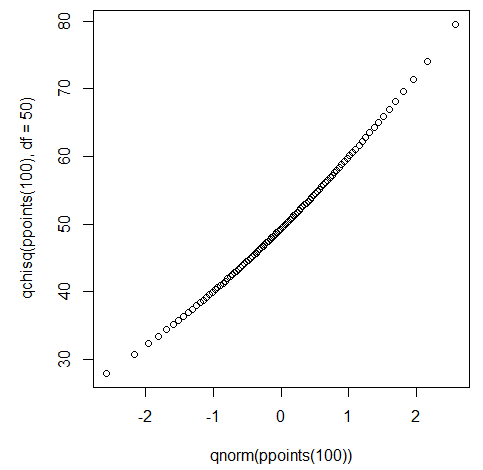
می‌دانیم که طبق قضیه حد مرکزی (Central Limit Theorem)، با افزایش درجه آزادی توزیع کای ۲، به توزیع نرمال نزدیک خواهیم شد. حال فرض کنید که تعداد مشاهده را به ۱۰۰ و درجه آزادی را هم برای توزیع کای ۲، برابر با ۵۰ در نظر بگیریم.

1qqplot(qnorm(ppoints(100)), qchisq(ppoints(100),df=50))

در نموداری که در تصویر زیر دیده می‌شود، به خوبی ارتباط خطی بین این دو متغیر دیده می‌شود زیرا نقاط روی یک خط راست قرار گرفته‌اند که از مبدا مختصات نیز گذشته است.

در مثال بعدی به بررسی یک توزیع دم-سنگین (Heavy Tails) با توزیع نرمال می‌پردازیم. یکی از معروف‌ترین توابع توزیع دم-سنگین، توزیع کوشی (Cauchy Distribution) است در نتیجه در اینجا هم از این توزیع داده تولید کرده و با توزیع نرمال، مقایسه می‌کنیم.

1qqplot(qnorm(ppoints(30)), qcauchy(ppoints(30)))

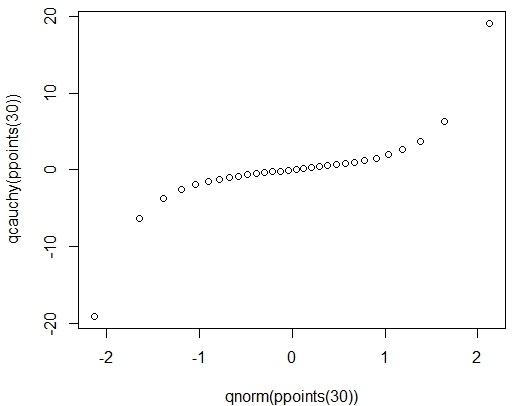
همانطور که در کد بالا مشاهده می‌کنید، تعداد ۳۰ مشاهده از توزیع نرمال و توزیع کوشی استاندارد تولید شده است و نمودار Q-Q plot برای آن‌ها ترسیم شده است.

از آنجایی که احتمال مشاهده مقادیر خیلی بزرگ یا خیلی کوچک در توزیع کوشی زیاد است، نمودار به صورتی که در تصویر زیر مشاهده می‌کنید در آمده است. مقدار احتمال برای داده‌های بسیار کوچک یا بسیار بزرگ در توزیع کوشی خیلی بزرگتر از توزیع نرمال استاندارد است در نتیجه نمودار حالتی شبیه مد یا ~ پیدا کرده است که نشان می‌دهد مقدار چندک‌های توزیع کوشی نسبت به توزیع نرمال در دم‌ها (مقادیر بزرگ و کوچک) بسیار تفاوت دارد.

خلاصه و جمع‌بندی

در این نوشتار به بررسی نمودار چندک-چندک یا Q-Q plot‌ پرداختیم و با نحوه محاسبه چندک و تفاوت آن با صدک‌ها آشنا شدیم. از طرفی مطابقت توزیع تجربی داده‌ها با یک توزیع دلخواه را مورد بررسی قرار دادیم. همینطور از روی شکل نمودار چندک-چندک یا Q-Q plot‌ مشخص کردیم که آیا داده‌ها دم-سنگین بوده یا دارای چولگی هستند. به این ترتیب راهکاری برای شناسایی رفتار داده‌های تصادفی براساس توزیع‌های آماری بدست آوردیم. این کار بخصوص برای مطابقت داده‌ها یا جمله خطا با توزیع نرمال که در تحلیل‌های رگرسیونی و واریانس که یک پیش‌فرض قوی است، کاربرد دارد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش برنامه‌ نویسی R و نرم‌ افزار RStudio
• توزیع‌های آماری — مجموعه مقالات جامع وبلاگ فرادرس
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها

^^