نظریه اعداد و کاربردهای آن – به زبان ساده

نظریه اعداد یک شاخه از ریاضیات محض است که به بررسی اعداد صحیح و توابع با مقدار صحیح می‌پردازد. نظریه اعداد و کاربردهای آن در بسیاری از علوم دیگر بخصوص علوم رایانه دیده می‌شود. در این نوشتار به بررسی این نظریه پرداخته و با کاربردهای آن آشنا می‌شویم.

بهتر است برای آشنایی بیشتر با مجموعه اعداد صحیح که زمینه کار نظریه اعداد است، نوشتارهای اعداد طبیعی — به زبان ساده و اعداد صحیح --- به زبان ساده را بخوانید. همچنین مطالعه الگوها و دنباله های متداول عددی – به زبان ساده و قواعد بخش پذیری یا عاد کردن — به زبان ساده نیز خالی از لطف نیست.

نظریه اعداد و کاربردهای آن

در اوایل قرن دوازدهم، علوم مرتبط با محاسبه را ریاضیات می‌نامیدند ولی از آن به بعد قسمتی از علم ریاضیات که به اعداد صحیح می‌پرداخت، تئوری یا نظریه اعداد نامیده شد. در این بین شناخت و کار روی اعداد صحیح بیشتر متمرکز شد و قضیه و نظریه‌های جدیدی نیز پدید آمد.

شاید ریشه نظریه اعداد را بتوان در نوشته‌های دانشمندان سومری پیدا کرد که روی لوح‌های گلی و 1800 سال قبل از میلاد، ثبت کرده‌اند. در یکی از این لوح‌ها، اعداد فیثاغورس نیز به چشم می‌خورد.

اعداد فیثاغورس، سه‌تایی‌هایی از اعداد طبیعی هستند که در قضیه فیثاغورس صدق می‌کنند. برای مثال 3، 4 و ۵ یک مجموعه از اعداد فیثاغورس هستند، زیرا:

$$\large 3^2+4^2=9+16=25=5^2$$

به بیان دیگر سه تایی $$(a,b,c)$$ را فیثاغورسی می‌نامند اگر:

$$\large a^2+b^2 =c^2$$

همانطور که می‌دانید این اعداد مرتبط با قضیه فیثاغورس هستند؛ اعداد بالا برای اضلاع یک مثلث قائمه‌الزاویه صدق می‌کنند.

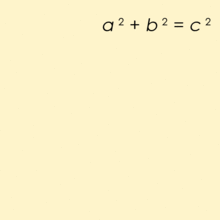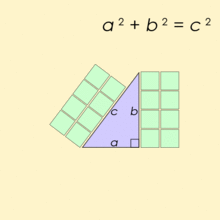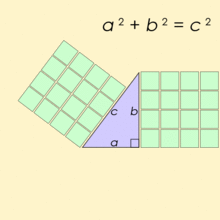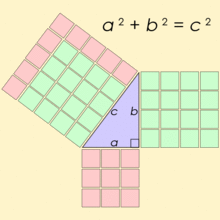
در نظریه اعداد، مبنا استفاده از اعداد صحیح و روابط بین آن‌ها است. به این ترتیب روش‌های پیدا کردن بزرگترین مقسوم علیه مشترک، تقسیم‌پذیری و عاد کردن، تجزیه به عوامل اول، تشخیص عدد اول و همنهشتی از قضیه‌هایی هستند که در نظریه اعداد مطرح می‌شوند.

نظریه اعداد مدرن

شاید بتوان «پیر دو فرما» (Pierre de Fermat) ریاضیدان شهیر فرانسوی (986 -1044 هجری شمسی) را رکن اساسی در پیشرفت نظریه اعداد در نظر گرفت. او که به اعداد کامل (Perfect numbers) علاقمند بود، روش‌های و الگوریتم‌های تقسیم عدد صحیح را ابداع کرد. فرما قضیه‌های زیادی را در نظریه اعداد (البته بدون اثبات) مطرح کرد که بعدا بعضی از آن‌ها توسط ریاضی‌دان‌های دیگر به اثبات رسید. شاید از نظر فرما این قضیه‌ها امری بدیهی بودند و اثبات آن‌ها برایش  بسیار ساده بود. در نتیجه اثبات‌ها را ثبت نکرد.

لئونهارد اویلر (Leonhard Euler) دانشمند آلمانی (1086-1162 هجری شمسی) نیز از کسانی بود که در پیشرفت نظریه اعداد نقش مهم داشت. بسیاری از قضیه‌های فرما توسط اویلر اثبات و تجزیه و تحلیل شد.

اصول و مفاهیم اولیه در نظریه اعداد

همانطور که در قبل اشاره کردیم، نظریه اعداد به مجموعه اعداد صحیح اختصاص دارد. این مجموعه به کمک عملگرهای جمع (+)، ضرب (×) و رابطه ترتیبی کوچکتر یا مساوی ($$\leq$$)، دستگاهی به نام دستگاه اعداد صحیح می‌سازد که آن را به شکل زیر نمایش می‌دهند.

$$\large (Z,+,\times,\leq)$$

چنین دستگاهی در «اصل خوش‌ترتیبی» (Well-Ordering Principle) صدق می‌کند.

اصل خوش‌ترتیبی

فرض کنید مجموعه $$S$$ یک زیر مجموعه ناتهی از اعداد صحیح باشد. اصل خوش‌ترتیبی بیان می‌کند که اگر این مجموعه از بالا (پایین) کران‌دار باشد، آنگاه حتما دارای عوض انتهایی (ابتدایی) خواهد بود.

مثال ۱

مجموعه  $$S=\{1,2,\ldots\}$$ را در نظر بگیری که همان مجموعه اعداد طبیعی است. واضح است که این مجموعه از پایین کران‌دار است. از طرفی این مجموعه، یکی از زیر مجموعه‌های اعداد صحیح نیز هست. مشخص است که یک (۱) عضو ابتدایی این مجموعه است.

مثال ۲

مجموعه $$S=\{\ldots,-2,-1\}$$ یک زیر مجموعه ناتهی از اعداد صحیح است. واضح است که $$S$$، مجموعه اعداد صحیح منفی را تشکیل می‌دهد. از آنجایی که این مجموعه از بالا کردان‌دار است، پس دارای عضو انتهایی است. همانطور که مشاهده می‌کنید، عضو انتهایی این مجموعه $$-1$$ است.

مثال ۳

مجموعه $$A=\{\ldots,-2,0,2,4,\ldots\}$$ زیر مجموعه اعداد صحیح است. ولی از بالا یا پایین کران‌دار نیست. در نتیجه اصل خوش‌ترتیبی برای این مجموعه به کار نمی‌رود.

به یاد دارید که اصول، پایه‌ها و اساس قضیه‌های ریاضی هستند و به کمک آن‌ها می‌توان مسئله و قضیه‌هایی مهمی را در مجموعه اعداد اثبات کرد.

خاصیت بسته بودن

یک مجموعه مانند $$S$$ را نسبت به عمل $$\oplus$$ بسته می‌گویند اگر برای هر دو عضو از این مجموعه رابطه زیر برقرار باشد.

$$\large \forall a,b \in S, \;\;a \oplus b \in S$$

به این معنی که اگر روی هر دو عضو از این مجموعه، عمل $$\oplus$$ را اجرا کنیم، نتیجه مقداری باشد که عضوی از مجموعه $$S$$ است. مجموعه اعداد صحیح، نسبت به عمل جمع، ضرب بسته است. در نتیجه با این مجموعه و این عملگرها می‌توان یک دستگاه اعداد ساخت.

مثال ۴

دو عضو از مجموعه اعداد صحیح مثل ۳ و ۵ را در نظر بگیرید. واضح است که مجموع این دو عدد 5+3=8‎ نیز یک عدد صحیح است و از طرفی 3 ×5 = 15 نیز عدد صحیح است. از سوی دیگر می‌توان یک رابطه ترتیبی بین اعضای مجموعه اعداد صحیح ایجاد کرد و به کمک آن‌ این مجموعه را مرتب کرد.

ویژگی‌های مجموعه اعداد صحیح در نظریه اعداد

از آنجایی که مجموعه اعداد صحیح بسیار پر کاربرد است و بخصوص در محاسبات روزانه نیز به کار می‌رود، دانشمندان و ریاضی‌دان‌ها، به ویژگی‌های آن پرداخته‌اند و بعضی از خصوصیات جالب این مجموعه اعداد را کشف کرده‌اند.

این ویژگی‌ها در ادامه فهرست شده‌‌اند.

• تقسیم‌پذیری در اعداد صحیح
• مجموعه خاصی از اعداد صحیح به نام اعداد اول
• هم‌نهشتی در اعداد صحیح
• توابع حسابی
• تقابل درجه دوم

در مورد هر یک از این ویژگی‌ها در ادامه توضیحات مختصری ارائه خواهد شد.

تقسیم‌پذیری در نظریه اعداد

یکی دیگر از مفاهیم و قضیه‌های مهم در نظریه اعداد، تقسیم‌پذیری یا بخش‌پذیری است که گاهی آن را عاد کردن نیز می‌نامند.

فرض کنید $$a$$ و $$b$$ دو عضو از مجموعه اعداد صحیح ($$Z$$) باشند. می‌گوییم $$a$$ بر $$b$$ بخش‌پذیر یا تقسیم‌پذیر است اگر رابطه زیر برقرار باشد.

$$\large \exists c \in Z, \;\; a= b\times c$$

و آن را به صورت $$b|a$$ نشان می‌دهیم و می‌خوانیم $$b$$، عدد $$a$$ را می‌شمارد یا عاد می‌کند.

به بیان دیگر رابطه بالا مشخص می‌کند که $$b$$، عدد $$a$$ را عاد می‌کند یا می‌شمارد. برای مثال برای ۲۰ و 4 که دو عدد صحیح هستند، می‌توان نوشت:

$$\large 20= 4 \times 5$$

زیرا

$$\large 20\div 4 = 5 \in Z$$

بهره‌گیری از خاصیت تقسیم‌پذیری برای اعداد صحیح، الگوریتم تقسیم را پدیده آورده است که به کمک آن عمل تقسیم برای اعضای مجموعه اعداد صحیح انجام می‌شود. این نحوه بخش کردن را تقسیم عدد صحیح می‌نامند که در آن، خارج قسمت و باقی‌مانده تقسیم، عدد صحیح بوده و باقی‌مانده نیز همیشه نامنفی است.

نکته: از الگوریتم تقسیم و خاصیت تقسیم‌پذیری برای اعداد صحیح، استفاده شده و بزرگترین مقسوم علیه مشترک (ب-م-م) محاسبه می‌شود.

بزرگترین مقسوم علیه مشترک

فرض کنید اعداد $$a_1,a_2,\ldots,a_n$$ که هیچ کدام صفر نیستند، مقادیر صحیح باشند. در این صورت اعضای مجموعه $$D_i$$ را مقادیری از اعداد صحیح مثل $$b$$ در نظر می‌گیریم که توسط $$a_i$$ عاد یا شمرده می‌شوند.

$$\large D_i= \{ b \in Z\;;\;\; b|a_i\}$$

برای مثال اگر $$a_1=2$$ باشد، $$D_1$$ شامل اعداد زوج در مجموعه اعداد صحیح خواهد بود زیرا همه اعداد زوج ($$b$$ها) بر ۲ بخش‌پذیرند. اگر $$a_2=6$$ باشد، مجموعه $$D_2$$ نشانگر اعضایی از اعداد صحیح است که مضربی از ۶ هستند.

حال اشتراک همه مجموعه‌های $$D_i$$ را محاسبه می‌کنیم و آن را $$S$$ می‌نامیم.

$$\large S=\cap_{i=1}^n D_i$$

واضح است که هر عضوی از $$S$$، مقادیری هستند که توسط $$b$$ شمرده می‌شوند. پس $$b$$ مقسوم علیه مشترک همه $$a_i$$ها است. بزرگترین عضو این مجموعه را بزرگترین مقسوم علیه مشترک $$a_i$$ها می‌نامیم و با نماد $$\gcd(a_1,a_2,\ldots,a_n)$$ نشان می‌دهیم.

مثال 5

برای اعداد ۱۸ و ۲۴ و ۶۴ بزرگترین مقسوم علیه مشترک، ۸ است، زیرا در این حالت $$a_1=18, a_2=24, a_3=64$$ و خواهیم داشت:

$$\begin{align} \large D_1=&\{1,2,3,6,9\}, \\ \large D_2=&\{1,2,3,6\}, \\ \large D_3=&\{1,2,3,6,9\} \end{align}$$

در نتیجه اشتراک آن‌ها به شکل زیر در خواهد آمد:

$$\large S=\cap_{i=1}^3 D_i=\{1,2,3,6\}$$

که بزرگترین عضو این مجموعه برابر است با ۶، پس عدد ۶ بزرگترین مقسوم علیه مشترک اعداد ۱۸ و ۲۴ و ۶۴ است.

نکته: مقسوم علیه‌های مشترک و ب-م-م منجر به مفهوم جدیدی به نام اعداد اول می‌شوند که به جز خودشان و ۱، هیچ مقسوم علیه مشترکی با دیگر اعضای مجموعه اعداد صحیح ندارند.

مجموعه اعداد اول

اعضای خاص از مجموعه اعداد صحیح را با نام اعداد اول می‌شناسیم. به کمک این اعداد می‌توان دیگر اعداد صحیح را ایجاد کرد. عدد صحیح و مثبت $$p$$ را اول گوییم اگر به جز خودش و ۱، هیچ شمارنده‌ای نداشته باشد. اعدادی در مجموعه اعداد صحیح که اول نیستند را به نام اعداد مرکب می‌شناسیم.

برای آنکه نشان دهیم چگونه از اعداد اول، بقیه اعداد صحیح ساخته می‌شوند به قضیه زیر توجه کنید.

قضیه: $$n>1$$ را در نظر بگیرید. حتما عدد اولی مانند $$p$$ وجود دارد که $$n$$ را می‌شمارد. به بیان ریاضی می‌توان نوشت:

$$\large p|n \rightarrow n = a \times p , a \in Z$$

اثبات: اگر $$n$$ یک عدد اول باشد که قضیه اثبات شده است. پس ابتدا آن را یک عدد مرکب در نظر می‌گیریم. پس $$n_1$$ و $$n_2$$ را اعداد صحیحی در نظر می‌گیریم که $$n$$‌ توسط حاصل‌ضرب آن‌ها ایجاد می‌شود.

$$\large n_1, n_2 \in Z\;, \;\; n=n_1\times n_2$$

اثبات در این گام بوسیله استقرا صورت خواهد گرفت. پس می‌توان هر عدد صحیح را به صورت حاصل‌ضرب یک عدد اول در نظر گرفت. این انگیزه‌ای برای قضیه اساسی یا بنیادی حساب خواهد شد. این قضیه نشان می‌دهد که هر عدد صحیح را می‌توان به عوامل یا حاصل ضرب اعداد اول تجزیه کرد.

نکته: دو عدد را نسبت به یکدیگر اول یا متباین (Coprime) می‌نامند اگر بزرگترین مقسوم علیه مشترک آن‌ها برابر با ۱ باشد. برای مثال عدد ۱۵ و ۱۴، متباین هستند زیرا بزرگترین مقسوم علیه مشترک آن‌ها ۱ است. در این حالت می‌نویسیم:

$$\large 15 \bot 14$$

و می‌خوانیم ۱۵ و ۱۴ نسبت به یکدیگر اول هستند. گاهی اعداد متباین را «هم‌اول» نیز می‌نامند.

اصل هم‌نهشتی در نظریه اعداد

با در نظر گرفتن خاصیت بخش‌پذیری برای اعداد صحیح، یک مفهوم جدید به نام هم‌نهشتی به میان می‌آید. دو عدد $$a$$ و $$b$$ را نسبت به پیمانه $$m$$ هم‌نهشت یا هم‌باقی‌مانده می‌نامند اگر رابطه زیر برقرار باشد.

$$\large m| (a-b)$$

می‌توان گفت که رابطه بالا نشان می‌دهد که حاصل تفاضل $$b$$ از $$a$$ به صورت مضربی از $$m$$ نوشته می‌شود. به این معنی که برای عدد مثبت $$m$$، باقی‌مانده تقسیم $$a$$ بر $$m$$ با باقی‌مانده تقسیم $$b$$ بر$$m$$ یکسان است. در این حالت می‌نویسیم.

$$\large a \equiv b (\operatorname{mod} m)$$

و می‌خوانیم $$a$$ با $$b$$ هم‌نهشت است به پیمانه $$m$$. همچنین می‌توانیم نماد $$a \equiv b (\operatorname{mod} m)$$‌ را به صورت زیر نیز بنویسیم.

$$\large a \equiv b (\operatorname{mod} m) \leftrightarrow \exists q \in Z\;;\;\; a-b = mq$$

رابطه هم‌نهشتی یک رابطه هم‌ارزی روی مجموعه اعداد صحیح $$Z$$ ایجاد می‌کند. یعنی داریم:

1. رابطه هم‌نهشتی دارای خاصیت بازتابی است. به این معنی که هر عضو از مجموعه اعداد صحیح، هم‌نهشت با خودش به پیمانه $$m$$ است. به بیان ریاضی $$\forall a \in Z, \;\;a \equiv a (\operatorname{mod} m)$$
2. رابطه همنهشتی دارای خاصیت تقارنی است. فرض کنید دو عدد $$a$$ و $$b$$ صحیح باشند. آنگاه رابطه هم‌نهشتی بین این دو را می‌توان جابجا کرد. به بیان ریاضی خواهیم داشت: $$\forall a, b \in Z,\;\; a\equiv b (\operatorname{mod} m) \rightarrow b \equiv a (\operatorname{mod} m)$$.
3. رابطه هم‌نهشتی دارای خاصیت ترایایی است. بنابراین اگر $$a$$ و $$b$$ و $$c$$ سه عدد صحیح و $$m$$ صحیح و مثبت باشد، بطوری که $$a$$ هم‌نهشت با $$b$$ به پیمانه $$m$$‌ و $$b$$ هم‌نهشت با $$c$$ به پیمانه $$m$$‌ باشد، می‌توان نتیجه گرفت که $$a$$ نیز هم‌نهشت با $$c$$ به پیمانه $$m$$‌ است. این رابطه را به زبان ریاضی به صورت زیر نشان می‌دهیم.

$$\forall a,b ,c , m \in Z, \;\; m>0;\;\;\;a \equiv b\,\, (\operatorname{mod} m)\; ,\; b \equiv c\,\, (\operatorname{mod} m)\, \rightarrow a\, \equiv c\,\, (\operatorname{mod} m )$$

مثال 6

دو عدد ۳۹ و ۲۵ به پیمانه ۷ هم‌نهشت هستند زیرا داریم:

$$\large 7|\overbrace{1\;\,4}^{39-25}$$

به این معنی که ۷ تفاصل این دو عدد (یعنی ۱۴) را می‌شمارد. به بیان دیگر تقسیم هر دو عدد ۳۹ و ۲۵ بر ۷ دارای باقی‌مانده برابری است.

$$\large \mod(39,7)= 4, \;\;\;\mod(25,7)=4$$

نکته: خارج قسمت این تقسیم‌ها به ترتیب برابر با ۵ و ۳ است. به یاد داشته باشید که خارج قسمت تقسیم و باقی‌مانده باید به صورت عدد صحیح بوده و باقی‌مانده هم مثبت باشد.

$$\large 25 \div 7 = 3, \;\; 39 \div 7 =5$$

همچنین به عنوان یک تعریف جدید کلاس هم‌ارزی $$a$$ را به صورت زیر تعریف می‌کنیم.

کلاس هم‌ارزی و هم‌نهشتی: کلاس هم‌ارزی $$a$$ نسبت به رابطه هم‌نهشتی به پیمانه $$m$$ را اعضایی از مقادیر اعداد صحیح مثبت می‌شناسیم که باقی‌مانده تقسیم اعداد صحیح بر $$m$$ با $$a$$ برابر است و آن را بوسیله $$[a]_m$$ نشان می‌دهیم. پس خواهیم داشت:

$$[a]_m = \{b \in Z ,\;\; a\;\equiv \; b (\operatorname{mod} m)\}$$

توجه داشته باشید که با توجه به تعریف هم‌نهشتی $$a$$ و $$b$$ بر پیمانه $$m$$ داریم:

$$\large a \equiv b (\operatorname{mod}\;m) \leftrightarrow \exists\; q \in Z; \;\; a-b = mq$$

پس خواهیم داشت:

$$[a]_m = \{a+mq;\,\, q \in Z\}$$

مثال ۷

در این مثال، مقادیری از مجموعه اعداد صحیح را مشخص می‌کنیم که به پیمانه ۲، هم‌نهشت هستند.

فرض کنید اعضای چنین مجموعه‌ای را با $$a$$ نشان دهیم. طبق الگوریتم تقسیم عدد صحیح داریم:

$$\large a = 2q+r, \;\; 0\leq r \leq 1$$

از آنجایی که مقدار $$r$$ باید یک عدد صحیح مثبت باشد، دو مقدار ۰ و ۱ برای آن در نظر گرفته می‌شوند.

$$\large a = 2q+0, \;\; [0]_2=\{a | \exists\;q ,\; a=2q\}=\{\ldots,-2,0,2,4,\ldots\}$$

که کلاس هم‌ارزی ۰ با اعداد بخش‌پذیر بر ۲ است، یا

$$\large a = 2q+1,\;\;[1]_2=\{a| \exists\;q, \; a=2q+1=\{\ldots,-3,-1,3,6,\ldots\}$$

که آن هم کلاس هم‌ارزی ۱ با اعداد بخش‌پذیر بر ۲ است. به این این ترتیب مجموعه [0] و [1] دارای اعضایی است که اختلاف هر دو عضو آن بر ۲ بخش‌پذیر است.

نکته: منظور از کلاس هم‌ارزی ۰، مجموعه‌ای است که باقی‌مانده تقسیم هر یک از اعداد آن برابر با صفر است. متناظر آن هم کلاس هم‌ارزی ۱ تعریف می‌شود.

کلاس‌ هم‌نهشتی دارای خواص زیر است:

1. هر کلاس هم‌نهشتی، ناتهی است.
2. اگر کلاس هم‌نهشتی $$[a]_m$$ و $$[b]_m$$ دارای نقاط مشترکی باشند، آنگاه رابطه $$a\equiv b (\operatorname{mod} m)$$. وجود دارد و برعکس به بیان دیگر شرط لازم و کافی برای آنکه $$[a]_m \cap [b]_m \neq \varnothing$$ آن است که $$a$$ و $$b$$ هم‌نهشت به پیمانه $$m$$ باشند.
3. اگر دو کلاس هم‌ارزی $$[a]_m$$ و $$[b]_m$$ برابر باشند، آنگاه $$a\equiv b (\operatorname{mod} m)$$. به این معنی که شرط آنکه دو کلاس هم‌ارزی به پیمانه $$m$$ برابر باشند آن است که $$a$$ و $$b$$ هم‌نهشت به پیمانه $$m$$ باشند.
4. کلاس‌های هم‌نهشتی به پیمانه $$m$$، مجموعه اعداد صحیح را افراز می‌کنند.
5. با توجه به مفهوم باقی‌مانده در تقسیم عدد صحیح، مشخص است که تعداد کلاس‌های هم‌نهشتی به پیمانه $$m$$ برابر است با $$m$$. به بیان دیگر داریم:

$$\large [0]_m,[1]_m,\ldots,[m-1]_m$$

مجموعه کلاس‌های هم‌نهشتی به پیمانه $$m$$ را با نماد $$Z_m$$ نشان می‌دهیم.

$$\large Z_m=\{[0]_m,[1]_m,\ldots,[m-1]_m\}$$

توابع حسابی در نظریه اعداد

تابعی مثل $$f$$ که دامنه آن مجموعه اعداد صحیح باشد، تابع حسابی نامیده می‌شود. ممکن است برد این تابع اعداد حقیقی یا اعداد مختلط باشد. در این صورت می‌نویسیم:

$$\large \cal{f}:\cal{Z}\rightarrow \cal{C}$$

به این معنی که تابع $$f$$ هر عضوی از اعداد صحیح را به یک عضو از اعداد مختلط تصویر می‌کند.

این گونه توابع در نظریه اعداد نقش مهمی دارند و به کمک آن‌ها می‌توانیم خصوصیات مجموعه اعداد صحیح را بهتر بشناسیم. یکی از توابع حسابی مهم در نظریه اعداد، تابع اویلر است که در ادامه معرفی می‌شود.

تابع فی اویلر (Euler's Totient Function)

تابع فی اویلر را با $$\varphi$$ نشان می‌دهند. این تابع به ازاء مقدار $$n>1$$، تعداد اعداد متباین نسبت به $$n$$ که مثبت بوده و از آن کوچکتر هستند را می‌شمارد.

مثال ۸

مقدار $$\varphi(9)= 6$$ زیرا اعداد $$1,2,4,5,7,8$$ همگی نسبت به $$9$$ هم‌اول (یا دارای بزرگترین مقسوم علیه مشترک برابر با ۱) هستند. تعداد اعضای این مجموعه نیز برابر است با ۶، پس مقدار تابع فی اویلر برای ۹ برابر است با ۶. به این ترتیب اگر gcd را بزرگترین مقسوم علیه مشترک در نظر بگیریم، داریم:

$$\large \gcd(9,1)=1,\;\;\gcd(9,2)=1,\;\;\gcd(9,4)=1,\;\;\gcd(9,5)=1,\;\;\gcd(9,7)=1,\;\;\gcd(9,8)=1$$

نکته: قرار داد می‌کنیم که $$\varphi(1)=1$$

در جدول زیر بعضی از مقادیر تابع فی اویلر را برای اعداد صحیح مثبت مشاهده می‌کنید.

همچنین نمودار زیر به نمایش تابع $$\varphi(n)$$ اختصاص دارد که برای هزار مقدار اول تابع فی اویلر را نشان می‌دهد.

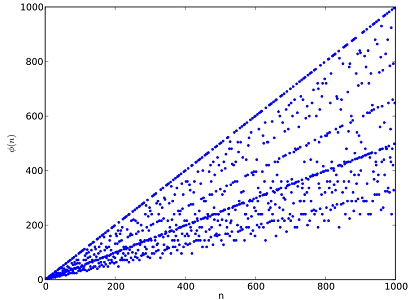
واضح است که برای هر عدد اول مثل $$p$$، مقدار تابع فی اویلر برابر است با $$p-1$$.

$$\large \varphi(p) = p-1, \;\; \text{p is prime.}$$

توابع دیگر مانند تابع موبیوس (Möbius function)‌ و تابع منگولد (Mangoldt function) از جمله توابع حسابی مشهور هستند.

قانون تقابل درجه دوم (Law of Quadratic Reciprocity)

موضوع تقابل درجه دوم، پیدا کردن اعداد صحیح است که به پیمانه عدد اول (به غیر از ۲)، مربع کامل باشند.

فرض کنید که عدد $$p>2$$، یک عدد اول باشد. همچنین در نظر بگیرید که $$p$$ یک عامل برای عدد صحیح $$a$$ نیست، یعنی $$p$$، عدد $$a$$ را عاد نمی‌کند یا نمی‌شمارد. اگر معادله هم‌نهشتی زیر دارای جواب باشد، آنگاه $$a$$ را مانده درجه دوم به پیمانه $$p$$ می‌گویند و در غیر اینصورت $$a$$ را نامانده به پیمانه $$p$$ می‌نامند.

$$\large x^2 \equiv a\;(\operatorname{mod}\;p)$$

مثال ۹

اعداد $$p=3$$ و $$a=13$$ را در نظر بگیرید.

$$\large x^2 \equiv 3\;(\operatorname{mod}\;13)$$

یعنی باید داشته باشیم:

$$\large 13| x^2-3$$

پاسخ‌های این رابطه هم‌نهشتی زمانی بدست می‌آیند که $$x^2-3=13$$، پس

$$\large x^2-3=13\rightarrow x^2=16 \rightarrow x^2=4^2 \rightarrow x=4$$

چون جواب این معادله هم‌نهشتی، یک عدد صحیح است، می‌گوییم، ۳ به پیمانه ۱۳ مانده درجه دوم است. البته واضح است که جواب دیگر این معادله هم‌نهشتی $$x=-4$$ است. می‌توان نشان داد که معادله هم‌نهشتی گفته شده، یا جواب ندارد یا فقط دو جواب خواهد داشت.

نماد لژاندر (Legendre Symbol) 

فرض کنید $$p$$ و $$q$$ دو عدد اول متمایز و مخالف ۲ باشند. واضح است که $$p$$، عدد $$q$$ را عاد نمی‌کند. یعنی

$$\large p \not{|} q$$

اگر $$p$$ به پیمانه $$q$$ مانده باشد، آنگاه نماد لژاندر به صورت زیر تعریف می‌شود.

$$\large {\displaystyle \left({\frac {q}{p}}\right)=\left\{{\begin{array}{rl}1&{\text{if }}\,n^{2}\equiv q\!{\pmod {p}}\,{\text{ for some integer }}n,\\-1&{\text{otherwise.}}\end{array}}\right.}$$

به این معنی که اگر $$q$$ به پیمانه $$p$$ مانده درجه دوم باشد، مقدار نماد برابر با ۱ و در غیر اینصورت مقدار ۱- را خواهد داشت.

مثال ۱۰

با توجه به محاسبات صورت گرفته در مثال ۹ مشخص است که خواهیم داشت:

$$\large \left(\frac{3}{13}\right) = 1$$

به این ترتیب قانون تقابل درجه دوم به صورت زیر نوشته می‌شود.

صورت قانون تقابل درجه دوم

برای دو عدد اول فرد $$p$$ و $$q$$ داریم:

$$\large \left({\frac {p}{q}}\right)\left({\frac {q}{p}}\right)=(-1)^{{\frac {p-1}{2}}{\frac {q-1}{2}}}$$

مثال ۱۱

به کمک مثال ۱۰ و ۹ می‌توان نوشت:

$$\large \left(\frac{3}{13}\right) = 1$$

$$\large \left(\frac{13}{3}\right) = 1$$

در نتیجه

$$\large \left({\frac {3}{13}}\right)\left({\frac {13}{3}}\right)=(-1)^{{\frac {13-1}{2}}{\frac {3-1}{2}}}=(-1)^{6\times 1}=1$$

خلاصه و جمع‌بندی

در این نوشتار با نظریه اعداد و قضیه‌ها و مفاهیم اولیه آن آشنا شدیم. مفاهیمی مانند بخش‌پذیری، اعداد اول و هم‌نهشتی از موضوعاتی هستند که در محاسبات و الگوریتم‌های رایانه‌ای به کار گرفته می‌شوند. نظریه اعداد نه تنها مبنایی برای رشد و توسعه علوم ریاضی و محاسباتی محسوب می‌شود بلکه بسیاری از موضوعاتی که در نظریه اعداد به کار می‌رود در توسعه علوم رایانه نیز نقش داشته‌اند. برای مثال در سیستم رمز‌نگاری RSA که یکی از روش‌های مرسوم برای رمز‌نگاری فایل‌ها و اطلاعات است از تابع فی اویلر برای ایجاد رمزها توسط اعداد اول استفاده می‌شود.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش ریاضی پایه دانشگاهی
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش‌دانشگاهی
• آموزش ریاضیات مهندسی
• تقسیم عدد صحیح — به زبان ساده
• الگوریتم تقسیم اعداد — از صفر تا صد
• قواعد بخش پذیری یا عاد کردن — به زبان ساده

^^