معادله صفحه مماس — به زبان ساده (+ دانلود فیلم آموزش رایگان)

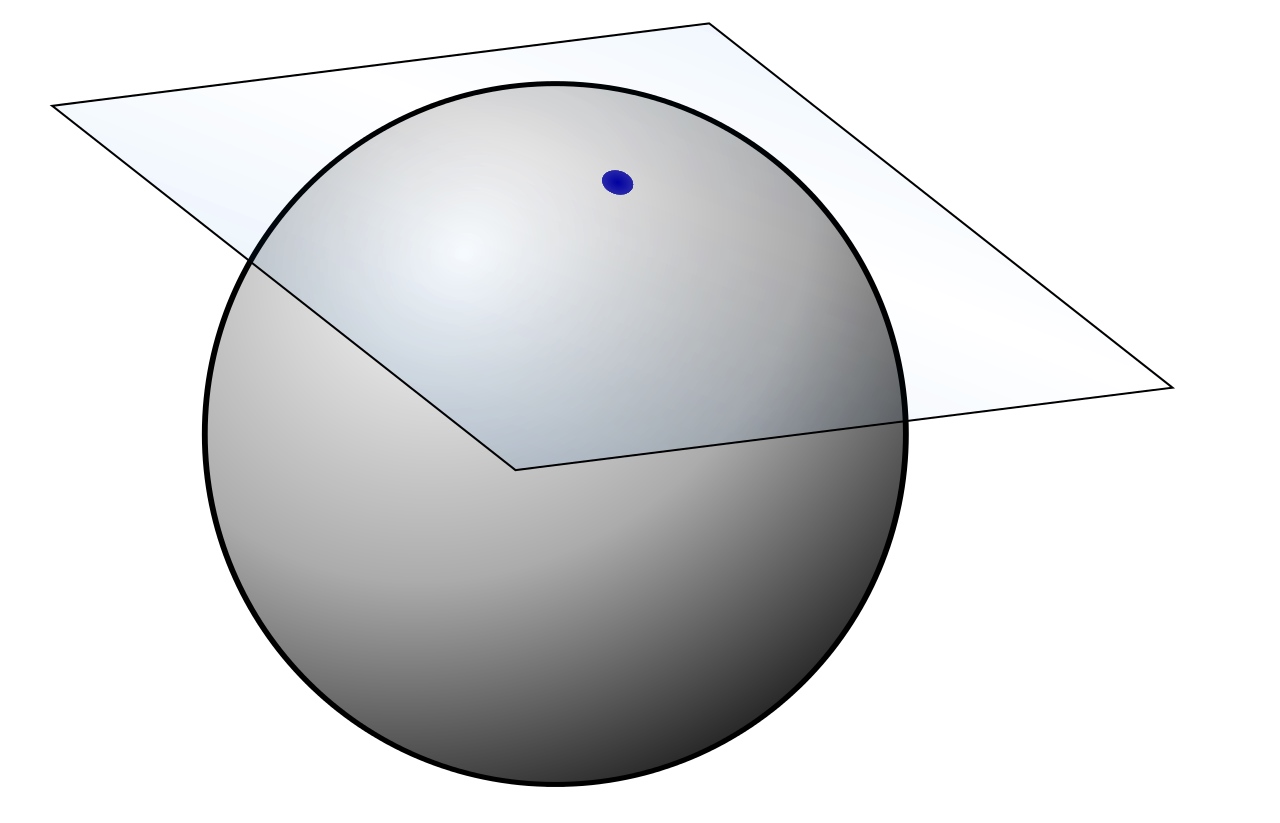
در مطلب مشتق جزئی بیان کردیم که چگونه مشتقات جهتی $$ f _ x , f _ y $$ نشان‌دهنده خطوط مماس بر تابع $$ f $$ هستند. در این مطلب قصد داریم تا حالت عمومی‌تر این مفهوم را بیان کرده و نحوه بدست آوردن معادله صفحه مماس را با استفاده از آن توضیح دهیم. نمودار تابع $$ z = f \left ( { x , y } \right ) $$، صفحه‌ای سه‌بعدی در $$ R ^ 3 $$ بوده از این رو می‌توان صفحه مماس بر آن را نیز در هر نقطه تعریف کرد.

فیلم آموزش معادله صفحه مماس — به زبان ساده (+ دانلود فیلم آموزش رایگان)

معادله صفحه مماس

در ابتدا فرض کنید $$ ( x _ 0 , y _ 0 ) $$ یک نقطه از صفحه بوده و $$ C _ 1 $$ نیز مسیری از $$ f ( x , y ) $$ روی صفحه $$ y = y _ 0 $$ باشد. به همین صورت $$ C _ 2 $$ نیز مسیری از $$ f ( x , y ) $$، روی صفحه $$ x = x _ 0 $$ است. در ابتدا باید یادآوری کنیم که $$ { f  _ x } \left ( { { x _ 0 } , { y _ 0 } } \right ) $$ نشان‌دهنده شیب خط مماس بر $$ f ( x , y ) $$ روی $$ C _ 1 $$ و $$ { f  _ y } \left ( { { x _ 0 } , { y _ 0 } } \right ) $$، نشان‌دهنده مماس بر $$ C _ 2 $$ است. هم‌چنین $$ L _ 1 $$ را برابر با خط مماس بر $$ C _ 1 $$ و $$ L _ 2 $$ را مماس بر $$ C _ 2 $$ در نظر بگیرید.

در این صورت صفحه مماس بر $$ f ( x , y ) $$، صفحه‌ای است که از هر دو خط $$ L _ 1 $$ و $$ L _ 2 $$ عبور کند. از نظر هندسی این صفحه دقیقا خاصیت‌های مشابه با خط مماس بر نمودار در یک نقطه را دارد. حال به منظور بدست آوردن معادله صفحه، فرض کنید نقطه $$ ( x _ 0, y _0 ) $$ روی صفحه $$ f ( x , y) $$ قرار گرفته است. با توجه به این‌که نقطه روی هر دو صفحه قرار گرفته، بنابراین می‌توان تساوی زیر را بیان کرد:

$$ \large \left ( { { x _ 0} , { y _ 0 } ,{ z _ 0 } } \right ) = \left (
{ { x _ 0 }, { y _ 0 } , f \left ( { { x _0 } , { y _0 } } \right ) } \right ) $$

از طرفی می‌دانیم که شکل عمومی معادله یک صفحه به صورت زیر است.

$$ \large a \left ( { x – { x _ 0 } } \right ) + b \left ( { y – { y _ 0 } } \right ) + c \left ( { z – { z _ 0 } } \right) = 0 $$

رابطه فوق با این فرض بیان شده که $$ \left ( { { x _ 0 } , { y _ 0 } , { z _0 } } \right ) $$ روی صفحه قرار داشته و $$ ( a , b , c ) $$، بردار عمود به صفحه باشد. معادله فوق را به شکل زیر بازنویسی می‌کنیم.

$$ \large z – { z _ 0 } = – \frac { a } { c } \left ( { x – { x _ 0 } } \right ) – \frac { b } { c } \left ( { y – { y _0 } } \right ) $$

با توجه به رابطه فوق ضرایب جدید $$ A , B $$ را به صورت زیر تعریف می‌کنیم.

$$ \large A = – \frac { a } { c } \hspace {0.25in} B = – \frac { b } { c } $$

بنابراین معادله را می‌توان به صورت زیر بازنویسی کرد.

$$ \large z – { z _ 0 } = A \left ( { x – { x _ 0 } } \right ) + B \left ( { y – { y _ 0 } } \right ) $$

در معادله فوق ضرایب $$ A , B $$ باید یافت شوند. بدین منظور در ابتدا فرض کنید $$ y $$ ثابت است. در این حالت اگر $$ y = { y _ 0 } $$ فرض شود، در این صورت معادله صفحه (که در بالا بیان شده)، به صورت زیر در خواهد آمد.

$$ \large z – { z _ 0 } = A \left ( { x – { x _ 0 } } \right ) $$

عبارت فوق نشان‌دهنده معادله خطی است که در نقطه $$ \left ( { { x _ 0 } , { y  _0 } } \right ) $$ به صفحه اصلی مماس است. در حقیقت مختصات تمامی نقاط قرار گرفته روی این خط، در $$ y = y _ 0 $$ قرار داشته و شیب این خط نیز برابر با $$ A $$ است. بنابراین می‌توان گفت معادله فوق نشان‌دهنده خط $$ L _ 1 $$ است. از طرفی می‌دانیم که شیب خط مماس به صفحه در یک نقطه مشخص برابر با $$ { f _ x } \left ( { { x _ 0 } , { y_ 0 } } \right ) $$ است. در حقیقت $$ A $$ را می‌توان به صورت زیر در نظر گرفت.

$$ \large A = { f _ x } \left ( { { x _0 } , { y _ 0 } } \right ) $$

به همین صورت می‌‌توان گفت با ثابت بودن $$ x $$ در $$ x = x _ 0 $$ نیز، $$ B $$ برابر است با:

$$ \large B = { f _ y } \left ( { { x _ 0 } , { y _0 } } \right ) $$

بنابراین نهایتا می‌توان معادله صفحه مماس بر $$ z = f \left ( { x , y } \right ) $$ در نقطه $$ ( x _ 0 , y _ 0 ) $$ را به صورت زیر بیان کرد:

$$ \large z – { z _ 0 } = { f _ x } \left ( { { x _ 0 } ,{ y _ 0 } } \right ) \left ( { x – { x _0 } } \right ) + { f _ y } \left ( { { x _0 } , { y _0 } } \right ) \left ( { y – { y _ 0 } } \right ) $$

با در نظر گرفتنِ $$ { z _ 0 } = f \left ( { { x _ 0 } , { y _ 0 } } \right ) $$، شکل نهایی معادله صفحه مماس برابر می‌شود با:

$$ \begin {align*} z – f \left ( { { x _ 0 } ,{ y _ 0 } } \right ) & = { f _ x } \left ( { { x _ 0 } , { y _ 0 } } \right ) \left ( { x – { x _ 0 } } \right) + { f _ y } \left ( { { x _ 0 } , { y _ 0 } } \right ) \left ( { y – { y _ 0 } } \right ) \\ z & = f\left ( { { x _ 0 }, { y _ 0 } } \right ) + {f_x}\left( { { x _ 0 },{ y _ 0 } } \right ) \left ( { x – { x _ 0 } } \right ) + { f _ y } \left( { { x _ 0 } , { y _0 } } \right ) \left( { y – { y _ 0 } } \right ) \end{align*}$$

مثال ۱

معادله صفحه مماس بر صفحه $$ z = \ln \left ( { 2 x + y } \right ) $$ را در نقطه $$ \left ( { – 1 , 3 } \right ) $$ بیابید.

به منظور یافتن معادله صفحه، کافی است، عبارت‌های مورد نیاز در عبارت فوق را بدست آورد. در ادامه این کار انجام شده است.

$$ \large \begin{align*}f\left ( { x , y } \right ) & = \ln \left ( { 2 x + y} \right ) \hspace {0.25in} & { z _ 0 } & = f \left ( { – 1 , 3 } \right) = \ln \left ( 1 \right ) = 0 \\ { f _ x } \left( {x,y} \right ) & = \frac { 2 } { { 2 x + y } } \hspace {0.25in} & { f _ x } \left ( { – 1,3} \right) & = 2 \\ {f_y}\left( { x , y } \right ) & = \frac { 1 } { { 2 x + y } } \hspace {0.25in} & { f _ y } \left( { – 1 , 3 } \right ) & = 1 \end {align*} $$

با توجه به مشتقات بدست آمده در بالا، معادله صفحه مماس برابر می‌شود با:

$$ \large \begin {align*}z – 0 & = 2 \left( { x + 1 } \right) + \left( 1 \right ) \left ( { y – 3 } \right ) \\ z & = 2 x + y – 1 \end {align*} $$

یکی از کاربرد‌های صفحه مماس این است که می‌توان با استفاده از آن‌ها معادله صفحه نزدیک یک نقطه را حدس زد. با توجه به این‌که به نقطه $$ \left ( { { x _ 0 } , { y _ 0 } } \right ) $$ نزدیک هستیم، بنابراین با استفاده از این معادله می‌توان مقدار تابع را در نقطه مذکور تقریب زد. بدین منظور تقریب خطی زیر را تعریف می‌کنیم.

$$ \large L \left ( { x , y } \right) = f\left ( { { x _ 0 } , { y _0 } } \right) + { f _ x } \left ( { { x _ 0 } , { y _ 0 } } \right ) \left( {x – { x _ 0 } } \right) + { f _ y } \left ( { { x_ 0 } , { y _ 0 } } \right ) \left( { y – { y _ 0 } } \right ) $$

با توجه به این‌که به نقطه $$ \left ( { { x _ 0 } ,{ y _ 0 } } \right ) $$ نزدیک هستیم، بنابراین می‌توانیم از تقریب زیر استفاده کنیم.

$$ f \left ( { x , y } \right ) \approx L \left ( { x , y } \right ) = f \left ( { { x _ 0 } , { y _0 } } \right) + { f _ x } \left ( { { x _ 0 } , { y _ 0 } } \right ) \left ( { x – { x _ 0 } } \right ) + { f _ y } \left ( { { x _ 0 } ,{ y _ 0 } } \right ) \left ( {y – { y _ 0 } } \right ) $$

مثال ۲

تقریب خطی صفحه زیر را در نقطه $$ \left ( { – 4 , 3 } \right ) $$ بیابید.

$$ \large z = 3 + \frac { { { x ^ 2 } } } { { 16 } } + \frac { { { y ^ 2 } } } { 9 } $$

در ابتدا باید معادله صفحه مماس را در نقطه مذکور بیابیم. بدین منظور در ابتدا مقادیر زیر را به منظور بدست آوردن معادله صفحه مماس محاسبه می‌کنیم.

$$ \large \begin{align*}f\left( {x,y} \right) & = 3 + \frac{ { { x ^ 2 } } } { { 1 6 } } + \frac { { { y ^ 2 } } } { 9 } \hspace{0.25in} & f\left( { – 4,3} \right) & = 3 + 1 + 1 = 5 \\ { f _ x } \left( {x,y} \right) & = \frac { x } { 8 } \hspace {0.25in} & {f_x}\left( { – 4,3} \right) & = – \frac { 1 } { 2 } \\ { f _ y } \left( { x , y } \right ) & = \frac { { 2 y } } { 9 } \hspace {0.25in} & { f _ y } \left ( { – 4 , 3 } \right ) & = \frac{2}{3}\end{align*}$$

بنابراین معادله صفحه مماس یا همان تقریب خطی برابر است با:

$$ \large L \left ( { x , y } \right ) = 5 – \frac { 1 } { 2 } \left ( { x + 4 } \right ) + \frac { 2 } { 3 } \left ( { y – 3 } \right ) $$

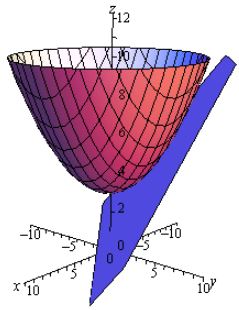
در ادامه شکل صفحه و مماس بر آن نشان داده شده‌اند.

مثال ۳

تقریب خطی سطح زیر و معادله صفحه مماس بر آن را در نقطه $$ \left ( { – 2 , 4 } \right ) $$ بیابید.

$$ \large z = 4 { x ^ 2 } – y { { \bf { e } } ^ { 2 x + y } } $$

همان‌طور که در بالا نیز بیان شد، تقریب خطی یک سطح سه‌بعدی در یک نقطه برابر با معادله صفحه در آن نقطه است. در ابتدا مشتقات مرتبه اول در جهات $$ x , y $$ را به صورت زیر بدست می‌آوریم:

$$ \large { f _ x } = 8 x – 2 y { { \bf{e}} ^ { 2 x + y } } \hspace {0.5in} \hspace{0.25in}{f_y} = – { { \bf{e}} ^ { 2 x + y } } – y { { \bf{e} } ^ { 2 x + y } } $$

هم‌چنین مقادیر تابع چندمتغیره در نقطه مذکور برابر است با:

$$ f \left ( { – 2 , 4 } \right ) = 12 \hspace {0.5in} { f _ x } \left ( { – 2 , 4 } \right ) = – 24 \hspace {0.5in} { f _ y } \left ( { – 2 , 4 } \right ) = – 5 $$

در نتیجه، تقریب خطی به صورت زیر خواهد بود:

$$\require{bbox} \bbox[2pt,border:1px solid black]{{L\left( {x,y} \right) = 12 – 24\left( {x + 2} \right) – 5\left( {y – 4} \right) = – 24x – 5y – 16}} $$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی و فیزیک
• مجموعه آموزش‌های ریاضی
• مجموعه آموزش‌های دروس دبیرستان و پیش‌دانشگاهی
• معادله صفحه – به زبان ساده
• ترکیب توابع — به زبان ساده

^^