حل معادله درجه دو – به زبان ساده + فیلم آموزش رایگان
در این مطلب از مجله فرادرس قصد داریم تا روش بدست آوردن پاسخ معادله درجه دوم را توضیح دهیم. ابتدا به ساکن لازم است تا با این نوع از معادلات آشنا باشید. معمولا جهت حل هر معادلهای از درجه ۳، ۴ و ... بایستی در ابتدا معادله را به شکل استاندارد بیان کرد.
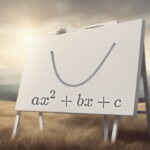
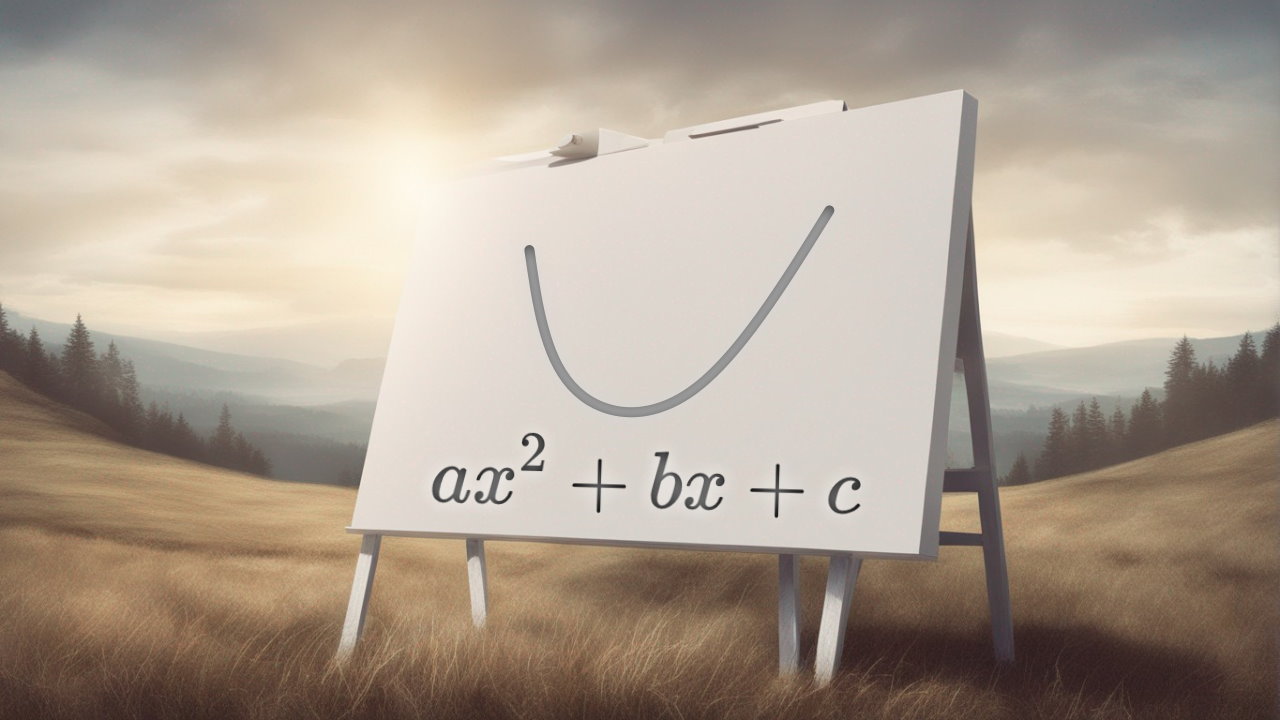
شکل معادله درجه دوم
جهت تعیین درجه یک معادله به بزرگترین توانِ متغیرِ آن نگاه کنید. اگر بزرگترین توان ۲ باشد، معادله نیز از مرتبه دوم یا به عبارتی از درجه دو است. برای نمونه معادله زیر یک معادله درجه دوم است چراکه بزرگترین متغیرِ (در این معادله x متغیر است) موجود در آن برابر با ۲ است.
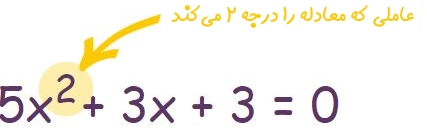
منحنی معادلات درجه دوم بهشکل زیر هستند.
البته توجه داشته باشید که خمیدگی منحنی ممکن است به سمت بالا نیز باشد.
شکل استاندارد
معمولا شکل استاندارد معادلات درجه دو بهصورت زیر بیان میشوند:
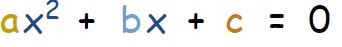
در رابطه بالا ضرایب a,b,c ثابت بوده و مقدار a غیرصفر است. همچنین x همان مجهولی است که هدف از حل کردن معادله یافتن آن است. در جدول زیر مثالهایی از معادلات درجه دوم ارائه شده است.

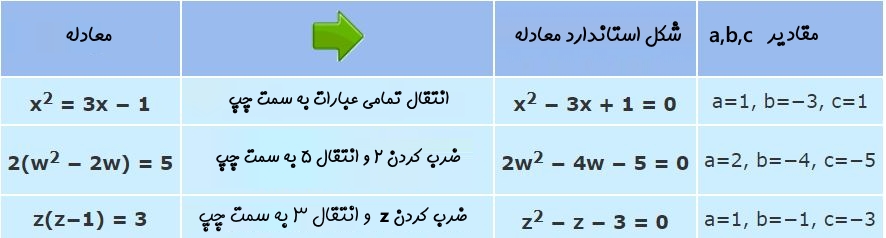
توجه داشته باشید که در مواقعی ممکن است شکل اولیهی معادله بهصورت استاندارد نباشد. در چنین حالاتی میتوان با جابجایی عبارات در طرفین معادله، شکل معادله را بهصورت استاندارد درآورد.
برای نمونه در جدول زیر تعدادی معادله ارائه شده که شکل اولیه آنها استاندارد نیست. همانطور که میبینید، در ستون سوم، شکل استاندارد این معادلات ارائه شده است.
حل معادله درجه دوم
منظور از پاسخ معادلهی درجه دوم، مقداری از x است که به ازای آن، پاسخ معادله برابر با صفر شود.
برای نمونه معادله x2-1=0 را در نظر بگیرید. اگر x=1 را در این معادله قرار دهیم، مقدار آن برابر با ۰=۱-۱۲ خواهد شد. بنابراین x=1 پاسخی برای معادله فوق محسوب میشود. توجه داشته باشید که یک معادله درجه دوم معمولا دارای دو پاسخ است. برای نمونه x=-1 نیز پاسخ معادله x2-1=0 است. حال معادلهای به شکل استاندارد (ax2+bx+c=0) را تصور کنید. در حالت کلی سه روش بهمنظور حل این معادله وجود دارد:
- فاکتورگیری
- مربع کامل
- استفاده از فرمول زیر
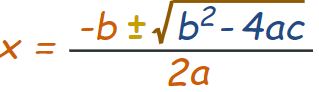
رابطه ۱
برای آشنایی بیشتر با فاکتورگیری و تجزیه چند جملهایها به مبحث «اتحاد و تجزیه در ریاضی — به زبان ساده» از مجله فرادرس مراجعه کنید.
اثبات پاسخ بدست آمده
شاید به نحوه یافتن رابطهی ارائه شده در روش شماره ۳ علاقهمند باشید. در ابتدا پیشنهاد میشود مطلبِ معادله دایره را مطالعه فرموده و در مورد نحوه بدست آمدن پاسخ شماره ۳ فکر کنید.
در اولین قدم طرفین رابطه را به a تقسیم کنید. با انجام این کار رابطه استاندارد بهصورت زیر در میآید.
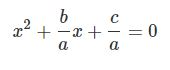
در قدم بعدی به طرفین رابطهی بالا، عدد را اضافه کنید. در نتیجه شکل عمومی رابطه فوق برابر خواهد بود با:
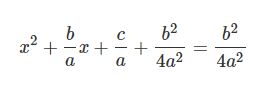
را نگه داشته و c/a را به سمت راست منتقل میکنیم. با انجام این کار رابطه بالا بهشکل زیر در میآید.
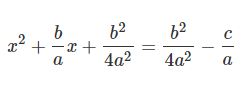
با توجه به مطلب معادله دایره، رابطه بالا یک دایره به شعاع را نشان میدهد. در حقیقت میتوان رابطه بالا را به شکل زیر بازنویسی کرد.
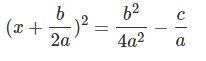
جهت بدست آوردن پاسخ x، از طرفین رابطه بالا جذر گرفته و آن را بهصورت زیر بازنویسی میکنیم.
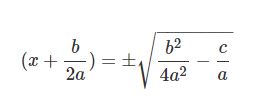
با نگه داشتن x و بردن b/2a به سمت راست، پاسخ x برابر با رابطه زیر بدست میآید.
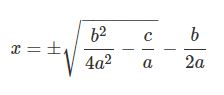
با فاکتور گرفتنِ ۱/۲a از سمت راستِ رابطهی بالا داریم:
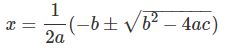
معمولا عبارت را بهصورت جداگانه با علامت (دلتا) نمایش میدهند؛ با این فرض رابطه فوق بهصورت زیر در خواهد آمد.
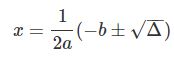
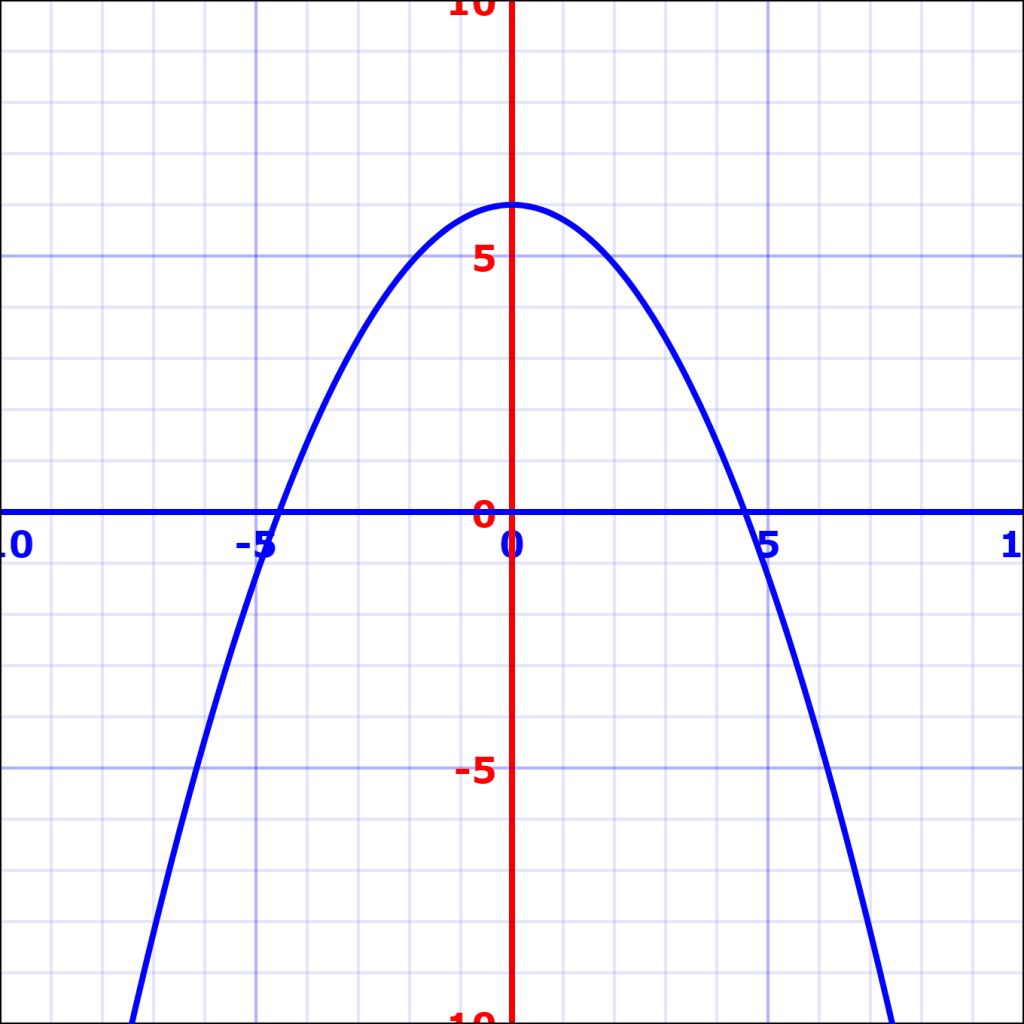
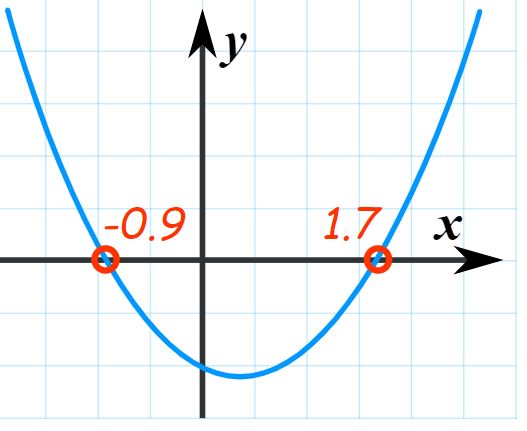
توجه داشته باشید که علامت ± به معنای این است که معادله درجه دوم دارای دو پاسخ است. در حقیقت محل تلاقی نمودار درجه دوم با محور xها همان پاسخ معادله است. همانطور که در شکل زیر نیز میبینید نمودار درجه دوم در دو نقطه محور xها را قطع کرده است.
اما اگر کل نمودار بالای محور xها قرار گیرد، نمودار محورها xها را در نقطهای قطع نمیکند؛ بنابراین پاسخها به چه شکل خواهند بود؟ در ادامه در این مورد توضیح خواهیم داد.
حالتهای مختلفِ
همانطور که در بالا نیز اشاره شد، در پاسخ x عبارت b2-4ac یا همان دلتا زیر رادیکال قرار میگیرد، در نتیجه این مقدار هر عددی نمیتواند باشد چراکه مقدار زیر رادیکال بایستی بیشتر از صفر باشد (۰< ). نهایتا برای یک معادله درجهی دوم حالتهای زیر میتواند رخ دهد:
- b2-4ac مثبت باشد. در این حالت معادله دو پاسخ متفاوت دارد.
- b2-4ac صفر باشد. در این حالت معادله دو پاسخ مشابه یا اصطلاحا ریشه مضاعف دارد.
- b2-4ac منفی باشد. در این حالت معادله پاسخی ندارد.
مثال ۱
پاسخ معادله 5x2+6x+1=0 را بیابید.
جهت حل یک معادلهی درجه دوم در ابتدا بایستی ضرایب a,b,c را بیابید.
با مقایسه معادله مذکور با معادله ax2+bx+c=0 مقادیر a,b,c برابر با اعداد زیر بدست میآیند.
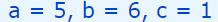
در قدم بعدی بایستی Δ را محاسبه کرده و علامت آن را مشخص کنید. با توجه به مقادیر a,b,c اندازه Δ برابر است با:
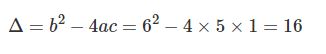
عدد بالا مثبت است؛ در نتیجه این معادله دارای دو پاسخ متفاوت خواهد بود. با استفاده از رابطه ۱، پاسخ معادله برابر است با:
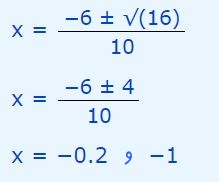
همانطور که انتظار میرفت معادله فوق دارای دو پاسخ است. البته نمودار رابطه فوق نیز همین امر را نشان میدهد. در حقیقت نمودار رابطه فوق بهشکل زیر است.
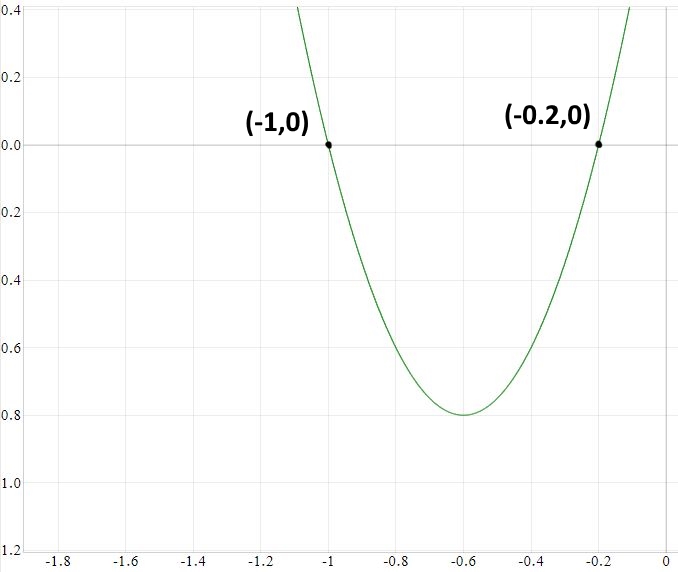
مثال ۲
پاسخ معادله 5x2+2x+1=0 را بیابید.
در رابطه فوق مقادیر a,b,c برابرند با:
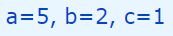
در نتیجه دلتا برابر است با:
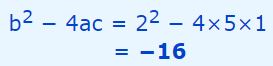
مقدار دلتای بدست آمده منفی است؛ بنابراین معادله فوق پاسخی در اعداد حقیقی ندارد.
خلاصه
- شکل عمومی یک معادله درجه دو بصورت ax2+bx+c=0 است.
- پاسخهای یک معادله درجه ۲ برابرند با:
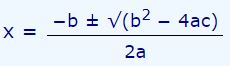
- در صورت مثبت بودن دلتا ()، معادله دارای دو پاسخِ متفاوت است.
- در صورتی که دلتا منفی باشد، معادله پاسخی ندارد.
- در صورتی که دلتا برابر با صفر باشد، معادله دو پاسخ یکسان یا اصطلاحا ریشه مضاعف دارد.
آزمون معادله درجه ۲
در این قسمت به منظور درک بهتر معادلات درجه ۲ و حل آنها، تعدادی پرسش چهار گزینهای به صورت آزمون تهیه شده است.
تمرین و آزمون
کدام گزینه ریشههای معادله زیر را به درستی نشان میدهد؟
هیچکدام
با استفاده از جایگزین زیر، معادله داده شده را به معادله درجه دو تبدیل میکنیم:
با قرار دادن جایگزین فوق در معادله ، داریم:
پاسخهای معادله بهدست آمده برابر و است. در پایان، u را در رابطه قرار میدهیم و ریشههای معادله را بهدست میآوریم.
بنابراین، ریشههای معادله اصلی برابر هستند با:
دو اتومبیل از نقطه یکسانی شروع به حرکت میکنند. اتومبیل A با سرعت ۴۰ کیلومتر برساعت به سمت شمال و سه ساعت بعد، اتومبیل B از همان نقطه با سرعت ۶۰ کیلومتر بر ساعت به سمت شرق شروع به حرکت میکند. چه مدت پس از آغاز حرکت اتومبیل A، فاصله دو اتومبیل از یکدیگر برابر ۵۰۰ کیلومتر میشود؟
حدود ۹ ساعت
حدود ۷ ساعت
حدود ۶ ساعت
حدود ۵ ساعت
بر طبق صورت مسئله، اتومبیل A با سرعت ۴۰ کیلومتر بر ساعت و اتومبیل B با سرعت ۶۰ کیلومتر بر ساعت حرکت میکنند. فرض کنید t مدت زمانی است که اتومبیل A حرکت میکند. اتومبیل B سه ساعت پس از اتومبیل A و از نقطه مشابهی شروع به حرکت میکند. این بدان معنا است که اتومبیل B در مدت زمان حرکت میکند. مسیر حرکت دو اتومبیل در تصویر زیر نشان داده شده است.
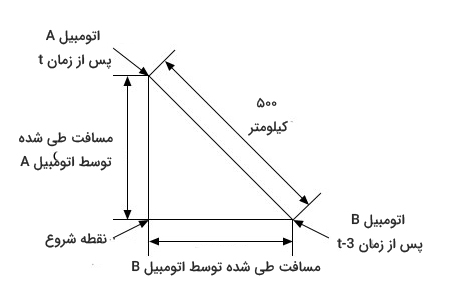
برای بهدست آوردن مدت زمان لازم برای آنکه فاصله دو اتومبیل از یکدیگر برابر ۵۰۰ کیلومتر شود، باید معادله مناسبی بنویسیم. به تصویر بالا توجه کنید. مسیر حرکت اتومبیلها نسبت به یکدیگر به شکل مثلث قائمالزاویهای است که وتر آن برابر ۵۰۰ کیلومتر است. بر طبق قضیه فیثاغورث، مجموع مربعات دو ضلع مجاور به وتر در مثلث قائمالزاویه برابر مربع وتر است.
بر طبق قوانین حرکت در فیزیک میدانیم مسافت طی شده توسط جسم برابر حاصلضرب تندی جسم به مدت زمان حرکت آن است.
بنابراین، برای هر اتومبیل داریم:
دو رابطه بالا را در رابطه قرار میدهیم:
به معادله درجه دو بر حسب t رسیدیم. ریشههای معادله را میتوانیم با استفاده از رابطه دلتا و به صورت زیر بهدست آوریم:
دو جواب برای t بهدست آمده است. زمان منفی است و از نظر فیزیکی هیچ معنایی ندارد. اما زمان مثبت و قابلقبول است. این بدان معنا است که در حدود ۹ ساعت پس از شروع حرکت اتومبیل A، فاصله دو اتومبیل از یکدیگر برابر ۵۰۰ کیلومتر میشود.
در معادله درجه دو حاصل (نسبت ریشه بزرگتر به کوچکتر) کدام است؟
برای حل معادله درجه دو ، از رابطه زیر استفاده میکنیم:
در معادله داده شده، مقدارهای a و b و c به ترتیب برابر یک، ۸- و ۵+ هستند. این مقدارها را در رابطه فوق قرار میدهیم:
در نتیجه، نسبت ریشه بزرگتر به کوچکتر یا برابر است با:
معادله را در نظر بگیرید، اگر این معادله دو ریشه و داشته باشد، کدام گزینه حاصل جمع م حاصل ضرب دو ریشه را به درستی نشان میهد؟
حاصل و به ترتیب برابر و است.
حاصل و به ترتیب برابر و است.
حاصل و به ترتیب برابر و است.
حاصل و به ترتیب برابر و است.
معادله را در نظر بگیرید. این معادله دو ریشه و دارد که با استفاده از رابطه زیر بهدست میآیند:
حاصل جمع دو ریشه و به صورت زیر بهدست میآید:
به طور مشابه، حاصلضرب دو ریشه و نیز به صورت زیر بهدست میآید:
در معادله مقدارهای e و f ریشههای معادلهاند. حاصل کدام است؟
طول مستطیلی یک متر کمتر از دو برابر عرض آن است. اگر مساحت مستطیل برابر ۱۰۰ متر مربع باشد، طول و عرض آن چه مقدار است؟
عرض مستطیل برابر ۷/۳۲۵۵ متر و طول آن برابر ۱۳/۶۵۱ متر است.
عرض مستطیل برابر ۵/۳۲۵۵ متر و طول آن برابر ۱۳/۶۵۱ متر است.
عرض مستطیل برابر ۷/۳۲۵۵ متر و طول آن برابر ۱۲/۶۵۱ متر است.
عرض مستطیل برابر ۷/۳۲۵۵ متر و طول آن برابر ۱۰/۶۵۱ متر است.
کدام گزینه ریشههای معادله زیر را به درستی نشان میدهد؟













سلام ممنونم بابت مطلب عالیت ، جواب سوال در چه صورت معادله درجه دو بزرگتر مساوی صفره ؟
با سلام خدمت شما؛
اگر a مثبت باشد، معادله در بیرون بازه بین دو ریشه یا برای همه xها بزرگتر مساوی صفر است. اما اگر a منفی باشد، معادله فقط بین دو ریشه (در صورت وجود) بزرگتر مساوی صفر خواهد بود.
از همراهی شما با مجله فرادرس سپاسگزاریم.
دست شما مرسی
Thanks a lot
کامل نبود، اگه میشه توضیح بدین اگر b یا a یا c مجهول بودن چه کاری باید انجامداد
از اینکه علم خود را به اشتراک میگزارید بسیار سپاس گزارم
Great
تولید معادله درجه ۲ با داشتن ریشه ها رو هم میشه توضیح بدین؟ چند ساله استفاده نکردم یادم رفته
عالی بود با تشکر از عوامل
با جاوا اسکریپت میشه نوشت به سادگی و تو یه خط :
function deltaQ(t, a, n) {
const [N, r, c, e, o] = [t, a, n, -1 * a, a ** 2 – 4 * t * n], s = Math.sqrt(o), [u, d] = [(e + s) / (2 * N), (e – s) / (2 * N)];
return [NaN != u ? u : “”, NaN != d ? d : “”]
}
console.log(deltaQ(5, 6, 1))
عالی هستید
مطالب درسیتون خیلی خوب توضیح داده شده
انصافا خیلی خوبه من از تابع متنفر بودم ولی خیلی ساده و روان توضیح دادی دمت گرم
ممنون بسیار عالی
متشکر از ویدئو
بعد بیست سال بالاخره فهمیدم چی به چیه
اگر دلتا ۰ باشه و ازمون تعداد ریشه ها رو بخواد میزنیم یک یا دو؟ یک ریشه مضاعف یل دو ریشه یکسان؟
عالیییییییییییییییییییییییییییی . بسیار ممنونم خیلی ساده ومفومی بود.
در کسب درآمد خیلی تاثیره این دلتا
دستتون درد نکنه ممنون
مرسی خوب بود
فقط من دوست داشتم علت بوجود آمدن دلتا رو بدونم و کجاها کاربرد داشته
برای چی
بسیار عالی و کاربردی