کاربرد معادلات دیفرانسیل در اقتصاد – به زبان ساده
در آموزشهای پیشین مجله فرادرس، با کاربرد بهینهسازی در اقتصاد آشنا شدیم. فرایندهای اقتصادی را میتوان با استفاده از دستگاه معادلات دیفرانسیل توصیف کرد. برای مثال، مدلی که در آن، قیمت، میزان فروش و موجودی کالا در انبار با یکدیگر ارتباط دارند و در طول زمان تغییر میکنند. در این آموزش، نمونهای از کاربرد معادلات دیفرانسیل در اقتصاد را بیان خواهیم کرد.


مثالی از کاربرد معادلات دیفرانسیل در اقتصاد
در یک بازار منعطف، میزان فروش به قیمت کالا یا خدمات بستگی دارد. این وابستگی را میتوان، برای مثال، به صورت زیر توصیف کرد:
که در آن، حجم فروش در واحد زمان، قیمت کنونی، قیمت تعادلی نزدیک به میانگین بازار و ضریب تناسب است. تابع نرخ فروش فعلی را نشان میدهد. بنابراین، حجم فروش محصول در بازه زمانی برابر با خواهد بود. بُعد ضریب به واحدهای و بستگی دارد. اگر و را کمیتهایی بدون بعد در نظر بگیریم و زمان را برحسب روز تعیین کنیم، واحد برابر با معکوس روز یا است.
معادله دیفرانسیل این سیستم چنین تعبیری دارد: تغییر نرخ فروش به اندازه انحراف قیمت فعلی از قیمت تعادلی بستگی دارد. ضریب را کوچکتر از صفر در نظر میگیریم (). بنابراین، در محدوده ، نرخ فروش در قیمتهای پایینتر افزایش خواهد یافت و بالعکس. چنین استراتژی بازاریابی تهاجمی اغلب در مواردی مانند فصل فروش یا جمعه سیاه مورد استفاده قرار میگیرد.

در پیادهسازی این روش، یک کسبوکار میتواند به اهداف دیگری نیز دست یابد: نگه داشتن موجوودی کالا در سطح قابل قبول پایین با تغییر قیمت کالا. این روش کنترل را میتوان با معادله دیفرانسیل زیر بیان کرد:
که در آن، ضریب تناسب و منفی است. در این حالت، قیمت با کمبود کالا افزایش خواهد یافت (برای ). بر هیمن اساس، وقتی باشد، قیمت با وجود کالای مازاد کم خواهد شد. واحد ضریب (مانند ضریب ) است.
برای تشکیل یک مدل کامل، لازم است یک معادله دیگر نیز بنویسیم که تعادل کالا در بازار را نشان میدهد:
که در آن، نرخ تأمین کالا توسط یک تولیدکننده یا تأمینکننده و نرخ فروش است که قبلاً درباره آن بحث کردیم.
در نتیجه، دستگاهی با سه معادله دیفرانسیل خواهیم داشت:
در ادامه، جواب عمومی را به دست میآوریم و رفتار توابع ، و را بررسی خواهیم کرد.
جواب عمومی دستگاه معادلات
دستگاه معادلاتی که به آن رسیدیم، یک دستگاه خطی ناهمگن با ضرایب ثابت است و میتوانیم آن را به فرم زیر بنویسیم:
که در آن:
$$ \large { \mathbf { Z } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { I \left ( t \right ) } \\<br /> { P \left ( t \right ) } \\<br /> { S \left ( t \right ) }<br /> \end {array} } \right ] , \; \; } \kern-0.3pt<br /> { A = \left [ { \begin {array} { * { 2 0 } { c } }<br /> 0 & 0 & { – 1 } \\<br /> \alpha & 0 & 0 \\<br /> 0 & \beta & 0<br /> \end {array}} \right] , \; \; } \kern-0.3pt<br /> { \mathbf { F } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> Q \\<br /> { – \alpha { I ^ * } } \\<br /> { – \beta { P ^ * } }<br /> \end {array} } \right ] . } $$
ابتدا جواب دستگاه همگن را به دست میآوریم. مقادیر ویژه ماتریس به صورت زیر به دست میآیند:
$$ \large \begin {align*} & \det \left ( { A – \lambda I } \right ) = 0 , \; \; \Rightarrow<br /> { \left | { \begin {array} { * { 2 0 } { c } }<br /> { – \lambda } & 0 & { – 1 } \\<br /> \alpha & { – \lambda } & 0 \\<br /> 0 & \beta & { – \lambda }<br /> \end {array} } \right | = 0 , \; \; } \\ & \Rightarrow<br /> { { \left ( { – \lambda } \right ) \left | { \begin {array} { * { 2 0 } { c } }<br /> { – \lambda } & 0 \\<br /> \beta & { – \lambda }<br /> \end {array} } \right | } - { \alpha \left | {\begin {array} { * { 2 0 } { c } }<br /> 0 & { – 1 } \\ \beta & { – \lambda }<br /> \end {array} } \right | = 0 , \; \; } } \\ & \Rightarrow<br /> { – \lambda \cdot { \lambda ^ 2 } – \alpha \cdot \beta = 0 , \; \; } \Rightarrow<br /> { – { \lambda ^ 3 } – \alpha \beta , \; \; } \\ & \Rightarrow<br /> { { \lambda ^ 3 } = – \alpha \beta , \; \; } \Rightarrow<br /> { { \lambda _ 1 } = – \sqrt [ \large 3 \normalsize ] { { \alpha \beta } } . } \end {align*} $$
همانطور که میبینیم، معادله مشخصه دارای ریشه تکراری مرتبه سوم با است. رتبه ماتریس به صورت زیر محاسبه میشود:
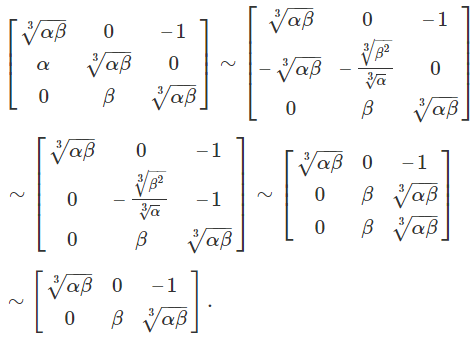
رتبه ماتریس ۲ است. بنابراین، تعدد هندسی برابر خوهد بود با:
این ماتریس با یک بلوک جردن با ابعاد توصیف میشود؛ یعنی ماتریس یک بردار ویژه عادی و دو بردار ویژه تعمیمیافته خواهد داشت.
برای به دست آوردن جواب، از روش ضرایب نامعین استفاده میکنیم. میخواهیم جواب را به فرم زیر بیابیم:
$$ \large { \mathbf { Z } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { I \left ( t \right ) } \\<br /> { P \left ( t \right ) } \\<br /> { S \left ( t \right ) }<br /> \end {array} } \right ] }<br /> = { { \mathbf { M } _ { k – s } } \left ( t \right ) { e ^ { { \lambda _ 1 } t } } }<br /> = { { \mathbf { M } _ { 3 – 1 } } \left ( t \right ) { e ^ { { \lambda _ 1 } t } } }<br /> = { { \mathbf { M } _ 2 } \left ( t \right ) { e ^ { { \lambda _ 1 } t } } } $$
که در آن، یک چندجملهای برداری است که در اینجا یک تابع درجه دوم است:
اکنون مقادیر ضرایب چندجملهای برداری را تعیین میکنیم. بردارهای ، و را با مختصات زیر در نظر بگیرید:
$$ \large \begin {align*}<br /> & { \mathbf { A } _ 0 } = \left [ { \begin {array} { * { 2 0 } { c} }<br /> { { a _ 0 } } \\<br /> { { b _ 0 } } \\<br /> { { c _ 0 } }<br /> \end {array}} \right ] , \; \; \kern-0.3pt<br /> { { \mathbf { A } _ 1 } = \left [ { \begin {array} { * { 20 } { c } }<br /> { { a _ 1 } } \\<br /> { { b _ 1 } } \\<br /> { { c _ 1 } }<br /> \end {array} } \right ] , \; \; } \kern-0.3pt<br /> { { \mathbf { A } _ 2 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 2 } } \\<br /> { { b _ 2 } } \\<br /> { { c _ 2 } }<br /> \end {array} } \right ] , \; \; } \\ & \Rightarrow<br /> { \mathbf { Z } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { I \left ( t \right ) } \\<br /> { P \left ( t \right ) } \\<br /> { S \left ( t \right ) }<br /> \end {array} } \right ] }<br /> = { \left [ { \begin {array} { *{ 2 0 } { c } }<br /> { \left ( { { a _ 0 } + { a _ 1 } t + { a _ 2 } { t ^ 2 } } \right ) { e ^ { { \lambda _ 1 } t } } } \\<br /> { \left ( { { b _ 0 } + { b _ 1 } t + { b _ 2 } { t ^ 2 } } \right ) { e ^ { { \lambda _ 1 } t } } } \\<br /> { \left ( { { c _ 0 } + { c _ 1 } t + { c _ 2 } { t ^ 2 } } \right ) { e ^ { { \lambda _ 1 } t } } }<br /> \end {array} } \right ] . }<br /> \end {align*} $$
بنابراین، مشتقها در معادلات به صورت زیر محاسبه میشوند:
با جایگذاری توابع ، و و مشتق آنها در دستگاه همگن و حذف ، خواهیم داشت:
$$ \large { \left \{ \begin {array} { l }<br /> \frac { { d I } } { { d t } } = – S \\<br /> \frac { { d P } } { { d t } } = \alpha I \\<br /> \frac { { d S } } { { d t } } = \beta P<br /> \end {array} \right . , \; \; } \kern0pt<br /> { \left \{ { \begin {array} { * { 2 0 } { l } }<br /> { { a _ 1 } + 2 { a _ 2 } t + { \lambda _ 1 } { a _ 0 } } + { { \lambda _ 1 } { a _ 1 } t + { \lambda _ 1 } { a _ 2} { t ^ 2 } } = { – { c _ 0 } – { c _ 1 } t – { c _ 2 } { t ^ 2 } } \\<br /> { { b _ 1 } + 2 { b _ 2 } t + { \lambda _ 1 } { b _ 0 } } + { { \lambda _ 1 } { b _1 } t + { \lambda _ 1 } { b _ 2 } {t ^ 2 } } = { \alpha { a _ 0 } + \alpha { a _ 1 } t + \alpha { a _ 2 }{ t ^ 2 } } \\<br /> { { c _ 1 } + 2 { c _ 2} t + { \lambda _ 1 } { c _ 0 } } + { { \lambda _ 1 } { c _ 1 } t + { \lambda _ 1 } { c _ 2 } { t ^ 2 } } = { \beta { b _ 0 } + \beta { b _ 1 } t + \beta { b _ 2 } { t ^ 2 } }<br /> \end {array} } \right . , \; \; }<br /> \\ \large<br /> \Rightarrow<br /> { \left \{ { \begin {array} { * { 2 0 } { l } } \\<br /> { { a _ 1 } + { \lambda _ 1 } { a _ 0 } = – { c _ 0 } } \\<br /> { 2 { a _ 2 } + { \lambda _ 1 } { a _ 1 } = – { c _ 1 } } \\<br /> { { \lambda _ 1 } { a _ 2} = – { c _ 2 } } \\<br /> { { b _1 } + { \lambda _ 1 } { b _ 0 } = \alpha { a _ 0 } } \\<br /> { 2 { b _ 2 } + { \lambda _ 1 } { b _ 1 } = \alpha { a _ 1 } } \\<br /> { { \lambda _ 1 } { b _ 2 } = \alpha { a _ 2 } } \\<br /> { { c _ 1 } + { \lambda _ 1 } { c _ 0 } = \beta { b _ 0 } } \\<br /> { 2 { c _ 2 } + { \lambda _ 1 } { c _ 1 } = \beta { b _ 1 } } \\<br /> { { \lambda _ 1 } { c _ 2 } = \beta { b _ 2 } }<br /> \end {array} } \right . . } $$
تساویهای ، و را در نظر میگیریم. سایر ضرایب را نیز برحسب ، و مینویسیم. همچنین میدانیم که مقدار ویژه است. بنابراین، داریم:
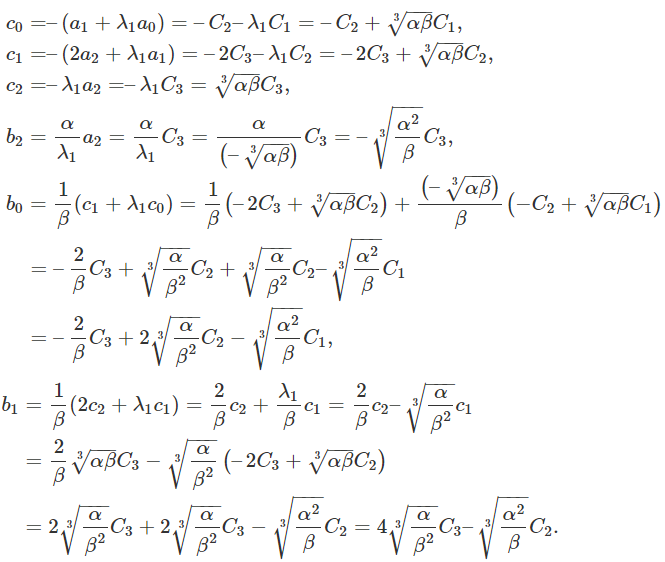
در نتیجه، جواب دستگاه معادلات همگن به صورت زیر خواهد بود:
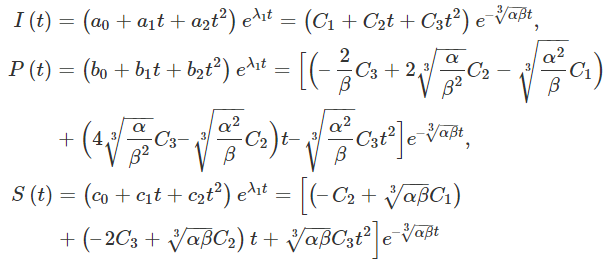
یا به فرم برداری، داریم:
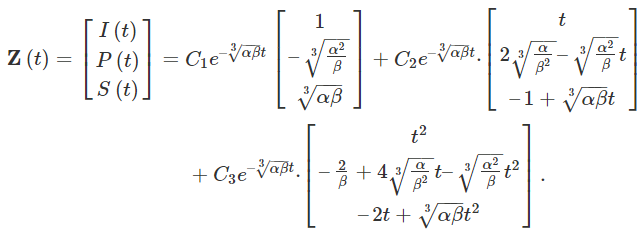
در ادامه، مقداری سادهسازی انجام میدهیم. ابتدا هر جمله را در ضرب کرده و پارامتر را در مختصات هر بردار وارد میکنیم:
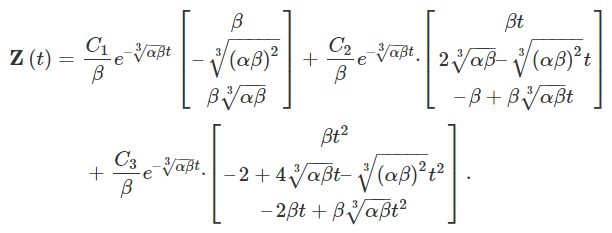
ضرایب دلخواه ، و را به صورت زیر تغییر میدهیم:
جواب شامل ۳ بردار مستقل خطی است. با نوشتن ، جواب عمومی به فرم زیر در میآید:
$$ \large \begin {align*}<br /> \mathbf { Z } \left ( t \right ) & = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { I \left ( t \right ) } \\<br /> { P \left ( t \right ) } \\<br /> { S \left ( t \right ) }<br /> \end {array} } \right ]<br /> = { { C _ 1 } { e ^ { – k t } } \left [ { \begin {array} { * { 2 0 } { c } }<br /> \beta \\<br /> { – { k ^ 2 } } \\<br /> { \beta k }<br /> \end {array} } \right ] }<br /> + { { { C _ 2 } { e ^ { – k t } } \left ( { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 0 \\<br /> { 2 k } \\<br /> { – \beta }<br /> \end {array} } \right ] } \right . } + { \left . { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \beta \\<br /> { – { k ^ 2 } } \\<br /> { \beta k }<br /> \end {array} } \right ] t } \right ) } } \\ &<br /> + { { { C _ 3 } { e ^ { – k t } } \left ( { \left [ { \begin {array} { * { 2 0 } { r } }<br /> 0 \\<br /> { – 2 } \\<br /> 0<br /> \end {array} } \right ] + \left [ { \begin {array} { * { 2 0 } { c } }<br /> 0 \\<br /> { 4 k } \\<br /> { – 2 \beta }<br /> \end {array} } \right ] t } \right . } } + { { \left . { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \beta \\<br /> { – { k ^ 2} } \\<br /> { \beta k }<br /> \end {array} } \right ] { t ^ 2 } } \right ) . } }<br /> \end {align*} $$
اکنون یک جواب خصوصی برای دستگاه ناهمگن به دست میآوریم. جمله ناهمگن دستگاه معادلات از ثوابت تشکیل شده است:
$$ \large \mathbf { F } = \left [ { \begin {array} { * { 2 0 } { c} }<br /> q \\<br /> { – \alpha { I ^ * } } \\<br /> { – \beta { P ^ * } }<br /> \end {array} } \right ] $$
جواب خصوصی را به فرمی مشابه زیر محاسبه میکنیم:
$$ \large { \mathbf { Z } _ 1 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { I _ 1 } } \\<br /> { { P _ 1 } } \\<br /> { { S _ 1 } }<br /> \end {array} } \right ] . $$
ثوابت ، و را به جای ، و قرار میدهیم:
$$ \large { \left\{ \begin {array} { l }<br /> \frac { { d I } } { { d t } } + S = q \\<br /> \frac { { d P } } { { d t } } – \alpha I = – \alpha { I ^ * } \\<br /> \frac { { d S } }{ { d t } } – \beta P = – \beta { P ^ * }<br /> \end {array} \right . , \; \; } \Rightarrow<br /> { \left \{ { \begin {array} { * { 2 0 } { l } }<br /> { { S _ 1 } = q } \\<br /> { – \alpha { I _ 1 } = – \alpha { I ^ * } } \\<br /> { – \beta { P _ 1 } = – \beta { P ^ * } }<br /> \end {array} } \right . , \; \; } \Rightarrow<br /> { \left \{ { \begin {array} { * { 2 0 } { l } }<br /> { { S _ 1 } = q } \\<br /> { { I _ 1 } = { I ^ * } } \\<br /> { { P _ 1 } = { P ^ * } }<br /> \end {array} } \right . . } $$
یک جواب خصوصی به شکل زیر به دست میآید:
$$ \large { \mathbf { Z } _ 1 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { I _ 1 } } \\<br /> { { P _ 1 } } \\<br /> { { S _ 1 } }<br /> \end {array} } \right ] = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { I ^ * } } \\<br /> { { P ^ * } } \\<br /> q<br /> \end {array} } \right ] . $$
بنابراین، جواب عمومی دستگاه ناهمگن اصلی را میتوانیم به صورت زیر بنویسیم:
$$ \large \begin {align*}<br /> \mathbf { Z } \left ( t \right ) & = { C _ 1 } { e ^ { – k t } } \left [ { \begin {array} {* { 2 0 } { c } }<br /> \beta \\<br /> { – { k ^ 2 } } \\<br /> { \beta k }<br /> \end {array} } \right ]<br /> + { { { C _ 2 } { e ^ { – k t } } \left ( { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 0 \\<br /> { 2 k } \\<br /> { – \beta }<br /> \end {array} } \right ] } \right . } + { \left . { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \beta \\<br /> { – { k ^ 2 } } \\<br /> { \beta k }<br /> \end {array} } \right ] t } \right ) } } \\ &<br /> + { { { C _ 3 } { e ^ { – k t } } \left ( { \left [ { \begin {array} { * { 2 0 } { r } }<br /> 0 \\<br /> { – 2 } \\<br /> 0<br /> \end {array} } \right ] + \left [ { \begin {array} { * { 2 0 } { c} }<br /> 0 \\<br /> { 4 k } \\<br /> { – 2 \beta }<br /> \end {array} } \right ] t } \right . } } + { { \left . { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \beta \\<br /> { – { k ^ 2 } } \\<br /> { \beta k }<br /> \end {array} } \right ] { t ^ 2 } } \right ) } }<br /> + { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { I ^ * } } \\<br /> { { P ^ * } } \\<br /> q<br /> \end {array} } \right ] . }<br /> \end {align*} $$
تحلیل جواب
فرمول بالا رفتار توابع ، و را توصیف میکند که به چند پارامتر وابسته است. مدل مورد نظر ما شامل پنج پارامتر ، ، ، ، و سه مقدار اولیه متغیرها است که آنها را با ، و نشان میدهیم.
حالتی را در نظر بگیرید که . در نتیجه، جواب عمومی به فرم زیر خواهد بود:
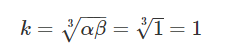
$$ \large \begin {align*}<br /> \mathbf { Z } \left ( t \right ) & = \left [ { \begin {array} { * { 2 0 } {c } }<br /> { I \left ( t \right ) } \\<br /> { P \left ( t \right ) } \\<br /> { S \left ( t \right ) }<br /> \end {array} } \right ]<br /> = { { C _ 1 } { e ^ { – t } } \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 1 } \\<br /> { – 1 } \\<br /> { – 1 }<br /> \end {array} } \right ] }<br /> + { { { C _ 2 } { e ^ { – t } } \left ( { \left [ { \begin {array} { * { 2 0 } { c} }<br /> 0 \\<br /> 2 \\<br /> 1<br /> \end {array} } \right ] } \right . } + { \left . { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 1 } \\<br /> { – 1 } \\<br /> { – 1 }<br /> \end {array} } \right ] t } \right ) } }<br /> \\ & + { { { C _ 3 } { e ^ { – t } } \left ( { \left [ { \begin {array}{ * { 2 0 } { r } }<br /> 0 \\<br /> { – 2 } \\<br /> 0<br /> \end {array} } \right ] + \left [ { \begin {array} { * { 2 0 }{ c } }<br /> 0 \\<br /> 4 \\<br /> 2<br /> \end {array} } \right ] t } \right . } } + { { \left . { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { – 1 } \\<br /> { – 1 } \\<br /> { – 1 }<br /> \end {array} } \right ] { t ^ 2 } } \right ) + \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { I ^ * } } \\<br /> { { P ^ * } } \\<br /> q<br /> \end {array} } \right ] . } }<br /> \end {align*} $$
یا
$$ \large { \mathbf { Z } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { I \left ( t \right ) } \\<br /> \color {red} { P \left ( t \right ) } \\<br /> \color {green} { S \left ( t \right ) }<br /> \end {array} } \right ] \text{ = }} { e ^ { – t } \cdot } \kern0pt<br /> { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { – { C _ 1 } – { C _ 2 } t – { C _ 3 } { t ^ 2} } \\<br /> \color {red} { { – { C _ 1 } + { C _ 2 } \left ( { 2 – t } \right ) } + { { C _ 3 } \left ( { – 2 + 4 t – { t ^ 2 } } \right ) } } \\<br /> \color {green} { { – { C _ 1 } + { C _ 2 } \left ( { 1 – t } \right ) } + { { C _ 3 } \left ( { 2 t – { t ^ 2 } } \right ) } }<br /> \end {array} } \right ] \; \; }<br /> + { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { { I ^ * } } \\<br /> \color {red} { { P ^ * } } \\<br /> \color {green} { q }<br /> \end {array} } \right ] . } $$
ثوابت ، و از شرایط اولیه به دست میآیند. در حالت کلی، فرض میکنیم:
$$ \large \mathbf { Z } \left ( 0 \right ) = \left [ { \begin {array}{ * { 2 0 } { c } }<br /> \color {blue} { I \left ( 0 \right ) } \\<br /> \color {red} { P \left ( 0 \right ) } \\<br /> \color {green} { S \left ( 0 \right ) }<br /> \end {array} } \right ] = \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { { I _ 0 } } \\<br /> \color {red} { { P _ 0 } } \\<br /> \color {green} { { S _ 0 } }<br /> \end {array} } \right ] . $$
بنابراین، ضرایب مذکور به صورت زیر به دست میآیند:
$$ \large { { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { – { C _ 1 } } \\<br /> \color {red} { – { C _ 1 } + 2 { C _ 2 } – 2 { C _ 3 } } \\<br /> \color {green} { – { C _ 1 } + { C _ 2 } }<br /> \end {array} } \right ] } + { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { { I ^ * } } \\<br /> \color {red} { { P ^ * } } \\<br /> \color {green} { q }<br /> \end {array} } \right ] = \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { { I _ 0 } } \\<br /> \color {red} { { P _ 0 } } \\<br /> \color {green} { { S _ 0 } }<br /> \end {array} } \right ] , \; \; } } \\ \large \Rightarrow<br /> { \left \{ { \begin {array} { * { 2 0 } { l } }<br /> {C _ 1 } = { I ^ * } – { I _0 } \\<br /> { { C _ 2 } = { S _ 0 } – q } + { { I ^ * } – { I _ 0 } } \\<br /> { { C _ 3 } = \frac { 1 } { 2 } \left ( { { P ^ * } – { P _ 0 } } \right . } + { \left . { { I ^ * } – { I _ 0 } } \right ) } + { { S _ 0 } – q }<br /> \end {array} } \right . } $$
در نتیجه، جواب در این حالت به صورت زیر است:
$$ \large { \mathbf { Z } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { I \left ( t \right ) } \\<br /> \color {red} { P \left ( t \right ) } \\<br /> \color {green} { S \left ( t \right ) }<br /> \end {array} } \right ] \text { = }} { e ^ { – t } \cdot } \kern0pt<br /> { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { – { C _ 1 } – { C _ 2 } t – { C _ 3 } { t ^ 2 } } \\<br /> \color {red} { { – { C _ 1 } + { C _ 2 } \left ( { 2 – t } \right ) } + { { C _ 3 } \left ( { – 2 + 4 t – { t ^ 2 } } \right ) } } \\<br /> \color {green} { { – { C _ 1 } + { C _ 2 } \left ( { 1 – t } \right ) } + { { C _ 3 } \left ( { 2 t – { t ^ 2 } } \right ) } }<br /> \end {array} } \right ] \; \; }<br /> + { \left [ { \begin {array} { * { 2 0 } { c } }<br /> \color {blue} { { I ^ * } } \\<br /> \color {red} { { P ^ * } } \\<br /> \color {green} { q }<br /> \end {array} } \right ] } $$
که در آن:
$$ \large { \left \{ { \begin {array} { * { 2 0 } { l } }<br /> { C _ 1 } = { I ^ * } – { I _ 0 } \\<br /> { { C _ 2 } = { S _ 0 } – q } + { { I ^ * } – { I _ 0 } } \\<br /> { { C _ 3 } = \frac { 1 } { 2 } \left ( { {P ^ * } – { P _ 0 } } \right . } + { \left . { { I ^ * } – { I _ 0 } } \right ) } + { { S _ 0 } – q }<br /> \end {array} } \right . } $$
شکل زیر نمودارهای رایج سطح موجودی ، قیمت و حجم فروش را نشان میدهد. این منحنیها، متناظر با پارامترهای زیر هستند:
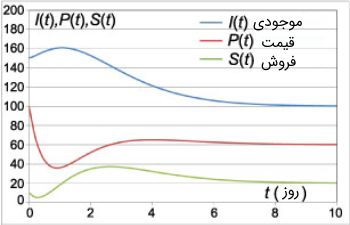
همانطور که در این نمودارها مشخص است، بعد از فرایند گذار، همه کمیتهای دینامیکی به مقادیر مجانبیشان میل میکنند که به مؤلفه ناهمگن بستگی دارد. وقتی مقدار ویژه منفی باشد، آنگاه جواب صفر دستگاه همگن پایدار مجانبی است. این، منجر به این واقعیت میشود که بخش همگن جواب در طول زمان «تضعیف شود» و توابع ، و ، صرفنظر از شرایط اولیه، به مقادیر مجانبیشان میل کنند. بنابراین، در این مدل میتوان موجودی را با استفاده از ساز و کار انعطاف پذیر برای تغییرات قیمت در یک سطح از پیش تعیین شده مشخص نگه داشت.












