ساخت و آموزش مدل های یادگیری ماشین در پایتون — راهنمای گام به گام
در یادگیری ماشین، مدلها برای آموزش الگوها، ارتباطات، اطلاعات موجود در داده و استفاده از آن برای پیشبینی ویژگی/ویژگیهای هدف کاربرد دارند. برای مثال، یک مدل میتواند ارتباط متغیرهای مختلف آناتومیک با اضافه وزن را یاد گرفته و بر همین اساس، میزان اضافه وزن افراد را پیشبینی کند. در این مطلب، با ایجاد و آموزش مدل های یادگیری ماشین در پایتون آشنا میشویم.
آموزش مدل های یادگیری ماشین
برای آموزش یک مدل، به چهار بخش عمده نیاز داریم:
- یک مجموعه داده با اندازه کافی برای آموزش
- یک مدل با روابط ریاضیاتی لازم
- یک تابع هزینه برای تعیین عملکرد مدل
- یک الگوریتم برای کمینه کردن تابع هزینه (یادگیری مدل)
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
آموزش مدل های یادگیری ماشین در پایتون
وارد محیط برنامهنویسی شده و 4 قدم گفته شده را به ترتیب طی میکنیم تا یک مدلسازی انجام دهیم.
ابتدا کتابخانههای مورد نیاز را فراخوانی میکنیم:
1import numpy as np
2import scipy.optimize as opt
3import matplotlib.pyplot as pltکتابخانههای فراخوانی شده، برای موارد زیر استفاده خواهند شد:
- کار با آرایهها:
- ایجاد داده
- توصیف مدل
- محاسبه خطا
- بهینهسازی تابع هزینه
- رسم نمودار:
- رسم نمودار دادهها
- رسم نمودار نتایج
قبل از شروع، تنظیمات زیر را اعمال میکنیم:
1np.random.seed(0)
2plt.style.use('ggplot')حال میتوانیم مجموعه داده مورد نیاز را تولید کنیم. برای شروع کار، یک مجموعه داده با یک ویژگی ورودی و یک ویژگی هدف ایجاد میکنیم. رابطه بین این دو ویژگی را به شکل زیر تعریف میکنیم:
$$ \large y=2x-1+e $$
در این رابطه، بخش $$e$$ نشاندهنده یک مقدار Noise با میانگین $$0$$ و واریانس $$0.3$$ است.
برای ایجاد دادهها، ابتدا تعداد را تعیین میکنیم:
1nD = 200 # Dataset Sizeحال میتوانیم $$X$$ را به صورت تصادفی در بازه $$[-2,+2]$$ ایجاد کنیم:
1X = np.random.uniform(-2, +2, (nD, 1))توجه داشته باشید که بازه انتخاب شده میتواند هر مقداری باشد.
نکته دیگری که وجود دارد، ستونی بودن دادهها است. به عنوان یک استاندارد، همواره دادهها در سطرها قرار میگیرند.
حال میتوانیم براساس رابطه گفته شده، $$Y$$ را تعریف کنیم:
1Y = 2*X - 1 + np.random.normal(0, 0.3, (nD, 1))به این شکل، عملیات ضرب عدد در بردار و جمع کردن دو بردار به راحتی توسط کتابخانه Numpy قابل انجام است.
حال یک Scatter Plot برای دادهها رسم میکنیم تا به صورت بصری ارتباط بین آنها را مشاهده کنیم:
1# Visualizing Created Dataset
2plt.scatter(X[:, 0], Y[:, 0], s=12)
3plt.title('Created Dataset (y = 2x - 1 + e)')
4plt.xlabel('X')
5plt.ylabel('Y')
6plt.show()با اجرای کد، نمودار زیر حاصل میشود.
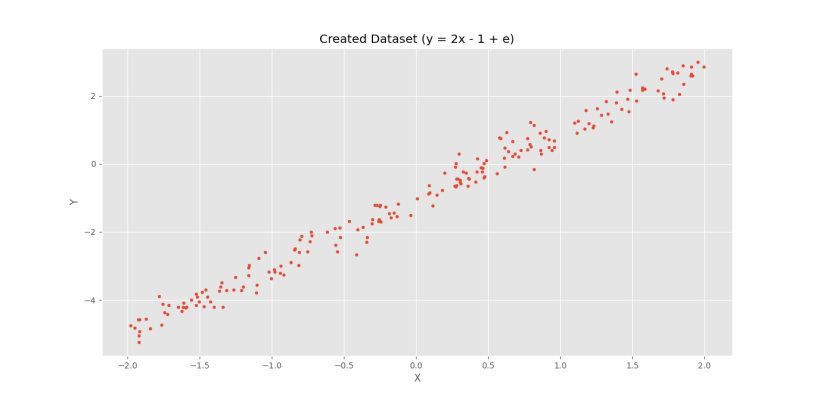
به این ترتیب، رابطه خطی تعریف شده بین ویژگیها مشاهده میشود.
برای مصارف بعدی، دادهها را به دو قسمت آموزش و آزمایش تقسیم میکنیم:
1trX = X[:160]
2trY = Y[:160]
3teX = X[160:]
4teY = Y[160:]حال مدلی برای توصیف رابطه ایجاد میکنیم:
$$ \large \hat{y}=p_{0}+p_{1} x $$
حال میتوان رابطه را به شکل بردار در قالب یک تابع توصیف کرد:
1def LinearModel(P:np.ndarray, X:np.ndarray):
2 Yh = P[0] + P[1]*X
3 return Yhاین تابع با گرفتن ماتریس پارامترها و ماتریس ویژگیهای ورودی، میتواند پیشبینیها را ارائه دهد.
حال میتوانیم یک تابع نیز برای محاسبه هزینه بنویسیم که در ورودی پارامترها، مدل و مجموعه داده را دریافت میکند:
1def Loss(P:np.ndarray, Model:function, X:np.ndarray, Y:np.ndarray):ابتدا پیشبینیهای مدل را برای دادههای ورودی محاسبه میکنیم:
1def Loss(P:np.ndarray, Model:function, X:np.ndarray, Y:np.ndarray):
2 Yh = Model(P, X)حال میتوانیم ماتریس خطا را محاسبه کنیم:
1def Loss(P:np.ndarray, Model:function, X:np.ndarray, Y:np.ndarray):
2 Yh = Model(P, X)
3 E = np.subtract(Y, Yh) # Errorتوجه داشته باشید که استفاده از عبارت $$E=Y-Yh$$ نیز نتایج یکسانی را به همراه خواهد داشت.
حال میتوانیم میانگین مربعات خطا را به شکل زیر محاسبه و علاوه بر نشان دادن در خروجی، با استفاده از return برگردانیم:
1def Loss(P:np.ndarray, Model, X:np.ndarray, Y:np.ndarray):
2 Yh = Model(P, X)
3 E = np.subtract(Y, Yh) # Error
4 SE = np.power(E, 2) # Squared Error
5 MSE = np.mean(SE) # Mean Squared Error
6 print(f'MSE: {MSE}')
7 return MSEحال میتوانیم بخش نهایی یعنی آموزش مدل را پیادهسازی کنیم.
توجه داشتی باشید که میتوان مستقیما از عبارت MSE=np.mean((Y-Yh)**2) استفاده کرد.
به این منظور، ابتدا تعداد پارامترهای مدل را تعیین میکنیم:
1nP = X.shape[1] + 1 # Parameters Countتوجه داشته باشید که در یک مدل خطی، به تعداد ویژگیهای ورودی به علاوه یک عدد پارامتر داریم.
حال حدس اولیهای برای پارامترها ایجاد میکنیم:
1P0 = np.random.uniform(-1, +1, nP)حال میتوانیم مدل را آموزش دهیم:
1Result = opt.minimize(Loss, P0, args=(LinearModel, trX, trY), method='slsqp', options={'maxiter':20})توجه داشته باشید که اولین ورودی تابع Loss همواره باید پارامترهای قابل بهینهسازی باشد. برای تنظیمات بیشتر میتوان ورودیهای دیگر از جمله Method و Options را بررسی کرد.
در تابع minimize امکاناتی نیز برای بهینهسازی مقید و تعیین محدوده برای پارامترها وجود دارد. برای مطالعه بیشتر میتوان به Document ایجاد شده برای آن مراجعه کرد.
پس از اجرای برنامه، مقدار خطا از $$7.9113$$ شروع شده و به $$0.0831$$ ختم میشود. در متغیر Result موارد زیر را مییابیم:
fun: 0.08313030478433348 jac: array([1.67638063e-08, 5.58793545e-09]) message: 'Optimization terminated successfully' nfev: 11 nit: 3 njev: 3 status: 0 success: True x: array([-1.02449041, 1.97477539])
که در دیکشنری حاصل، موارد زیر مشاهده میشود:
- مقدار تابع در نقطه بهینه: fun
- ژاکوبین تابع نسبت به پارامترها در نقطه بهینه که اعدادی بسیار نزدیک به صفر هستند: jac
- پیام بهینهسازی: message
- تعداد دفعات فراخوانی تابع هزینه: nfev
- تعداد مراحل اجرای الگوریتم بهینهسازی: nit
- تعداد دفعات محاسبه ژاکوبین تابع هزینه: njev
- موقعیت نهایی: status
- موفقیت یا عدم موفقیت الگوریتم بهینهساز: success
- مقادیر بهینه محاسبه شده برای پارامترها که کمترین مقدار خطا را تولید میکنند: x
توجه داشته باشید که مقادیر آرایه x به مقادیر استفاده شده در ایجاد دادهها بسیار نزدیک است.
به این ترتیب، نتایج حاصل تفسیر میشود. به عنوان پارامتر نهایی، مقدار x را از دیکشنری Result استخراج میکنیم:
1P = Result['x']حال میتوانیم مقدار تابع هزینه را برای هر دو مجموعه داده آموزش و آزمایش، محاسبه و نمایش دهیم:
1trLoss = Loss(P, LinearModel, trX, trY)
2teLoss = Loss(P, LinearModel, teX, teY)
3
4print(f'{trLoss = }')
5print(f'{teLoss = }')که نتیجه زیر حاصل میشود:
trLoss = 0.08313030478433348 teLoss = 0.07915122756575343
به این ترتیب مشاهده میکنیم که مدل در مجموعه داده آزمایش نیز از دقت مناسبی برخوردار است.
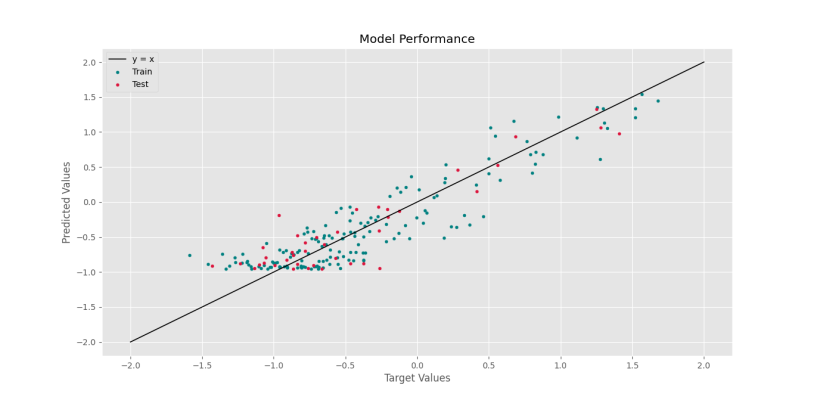
برای مشاهده نتایج، میتوانیم پیشبینیهای مدل را در مقابل مقادیر واقعی رسم کنیم. ابتدا پیشبینیهای مدل را محاسبه میکنیم:
1trPred = LinearModel(P, trX)
2tePred = LinearModel(P, teX)حال میتوانیم نمودارهای مورد نظر را رسم کنیم:
1# Visualizing Model Performance
2plt.scatter(trY[:, 0], trPred[:, 0], s=12, c='teal', label='Train')
3plt.scatter(teY[:, 0], tePred[:, 0], s=12, c='crimson', label='Test')
4plt.plot([-5, +3], [-5, +3], ls='-', lw=1.2, c='k', label='y = x')
5plt.title('Model Performance')
6plt.xlabel('Target Values')
7plt.ylabel('Predicted Values')
8plt.legend()
9plt.show()که پس از اجرا شکل زیر را خواهیم داشت.

به این ترتیب، مشاهده میکنیم که نتایج قابل قبول است.
به عنوان معیاری بهتر، میتوان ضریب تعیین یا R2 Score را بررسی کرد. برای آشنایی و پیادهسازی شریب تعیین، میتوانید به مطلب «بررسی معیارهای ارزیابی رگرسیون در پایتون — پیاده سازی + کدها» مراجعه کنید.
بنابراین برای تابع ضریب تعیین خواهیم داشت:
1def R2(Y:np.ndarray, Yh:np.ndarray):
2 e = np.subtract(Y, Yh)
3 se = np.power(e, 2)
4 mse = np.mean(se)
5 var = np.var(Y)
6 r2 = 1 - mse / var
7 return r2که برای استفاده از آن خواهیم داشت:
1trR2 = R2(trY, trPred)
2teR2 = R2(teY, tePred)
3
4print(f'{trR2 = }')
5print(f'{teR2 = }')پس از اجرا کد خواهیم داشت:
trR2 = 0.983469157490565 teR2 = 0.984689966890221
بنابراین، ضریب تعیین نیز عملکرد مناسب مدل را تایید میکند.
حال میتوانیم مجموعه دادهای متفاوت را ایجاد کنیم:
$$ \large y=-1+\exp(x-1)+e $$
برای ایجاد این مجموعه داده خواهیم داشت:
1nD = 200 # Dataset Size
2X = np.random.uniform(-2, +2, (nD, 1))
3Y = -1 + np.exp(X - 1) + np.random.normal(0, 0.3, (nD, 1))نمودار حاصل برای این مجموعه داده به شکل زیر خواهد بود.
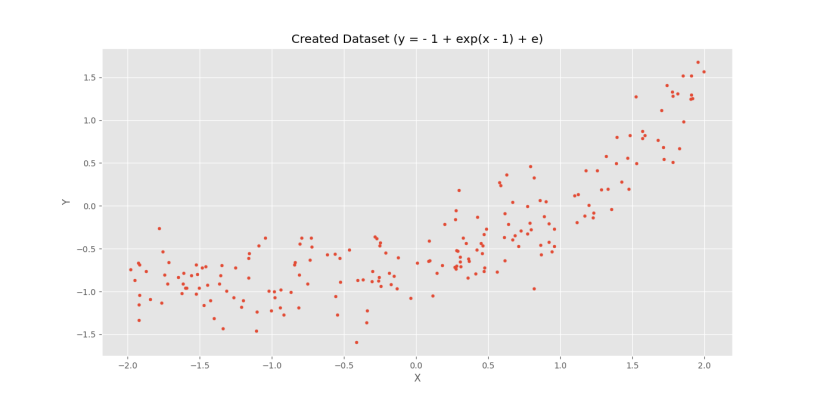
به این ترتیب، ارتباط بین دو ویژگی خط نبوده و اگر مدلی خطی روی آن آموزش دهیم، نتایج به شکل زیر خواهد بود.
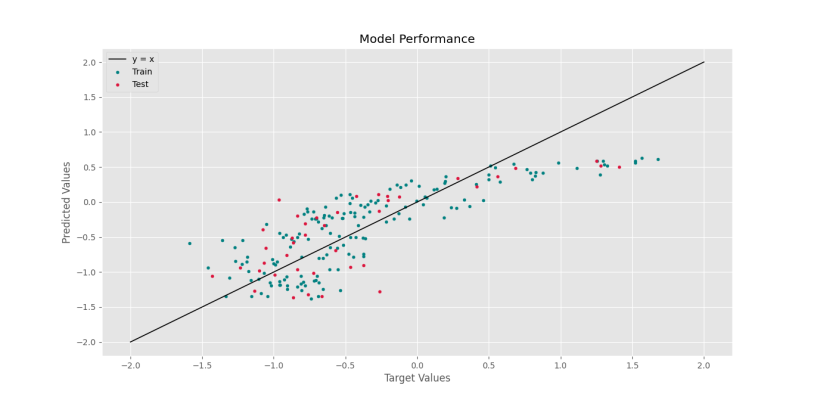
trR2 = 0.660279381206077 teR2 = 0.546179600118633
که مشاهده میکنیم نتایج مطلوب نیست. علت این مشکل، متناسب نبودن مدل ایجاد شده با داده است.
برای این شرایط میتوان مدلی به شکل زیر ایجاد کرد:
$$ \large \hat{y}=p_{0}+\exp \left(p_{1} x+p_{2}\right) $$
برای این حالت، مدلی به شکل زیر پیادهسازی میکنیم:
1def ExponentialModel(P:np.ndarray, X:np.ndarray):
2 Yh = P[0] + np.exp(P[1]*X + P[2])
3 return Yhحال بخشهایی که نیاز با تغییر دارند را بازنویسی میکنیم:
1nP = 3 # Parameters Count
2P0 = np.random.uniform(-1, +1, nP)
3Result = opt.minimize(Loss, P0, args=(ExponentialModel, trX, trY), method='slsqp', options={'maxiter':20})
4
5print(Result)
6
7P = Result['x']
8
9trPred = ExponentialModel(P, trX)
10tePred = ExponentialModel(P, teX)
11
12trLoss = Loss(P, ExponentialModel, trX, trY)
13teLoss = Loss(P, ExponentialModel, teX, teY)
14
15print(f'{trLoss = }')
16print(f'{teLoss = }')
17
18trR2 = R2(trY, trPred)
19teR2 = R2(teY, tePred)
20
21print(f'{trR2 = }')
22print(f'{teR2 = }')حال پس از اجرا نتایج زیر حاصل میشود.
trR2 = 0.8315934848317937 teR2 = 0.8247071754787298
که نتایج حاصل، عملکرد نسبتاً مناسب مدل را نشان میدهد.
برای نتایج بهینهسازی نیز دیکشنری زیر حاصل میشود:
fun: 0.08255973478479381 jac: array([0.00017609, 0.00039471, 0.00027515]) message: 'Optimization terminated successfully' nfev: 64 nit: 15 njev: 15 status: 0 success: True x: array([-1.01215658, 0.9614008 , -0.97999742])
مشاهده میکنیم که مقادیر ژاکوبین زیاد نتوانسته به خوبی به صفر نزدیک شود. از طرفی 15 مرحله الگوریتم کار کرده است. دلیل این اتفاق، پیچیده شدن مجموعه داده و زیاد شدن تعداد پارامترهای مدل است.
جمعبندی
در این مطلب، روش ایجاد داده، مدلسازی و آموزش مدل های یادگیری ماشین در پایتون را بررسی کردیم.
برای مطالعه بیشتر میتوان موارد زیر را بررسی کرد:
- توضیحات در مورد تابع optimize.minimize
- عملکرد الگوریتمهای مختلف در مسائل متفاوت
- اثر تعداد maxiter در جلوگیری از بیشبرازش (Overfitting)
- مدلسازیهای مختلف برای انواع ارتباط بین ویژگیها
- اثر تعداد داده بر سرعت آموزش مدل










