ماتریس افزوده – به زبان ساده (+ دانلود فیلم آموزش گام به گام)
در این مطلب قصد داریم تا روشی متفاوت را به منظور حل سیستمی از دستگاه معادلات ارائه دهیم. در این روش از ماتریسی تحت عنوان ماتریس افزوده استفاده میشود. البته در مطالب گذشته وبلاگ فرادرس روش کلی حل دستگاه معادلات خطی نیز توضیح داده شد که بهمنظور تسلط به مفهوم دستگاه معادلات میتوانید آن را مطالعه فرمایید.
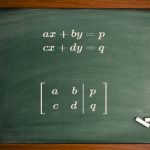

فیلم آموزشی ماتریس افزوده
ماتریس افزوده
بدیهی است که برای سیستمی از دو یا چند معادله خطی، حل کردن سیستمی از معادلات به نسبت یک معادله، مشکلتر بهنظر میرسد. ماتریس افزوده برای سیستمی از معادلات، به آرایهای از اعداد گفته میشود که هر ردیف ضرایب یک معادله و هر ستون ضرایب یک متغیر را نشان میدهند. برای نمونه دستگاه معادلات زیر را در نظر بگیرید.
ماتریس افزوده مربوط به معادلات بالا به صورت زیر بیان میشود.
توجه داشته باشید که ستون قرار گرفته در سمت راست خط جداکننده، ستون مربوط به پاسخهای معادلات هستند. در قدم بعدی باید ماتریس را تا حد ممکن ساده کرده، سپس معادلات را حل کرد. در ادامه در قالب ماتریس ارائه شده در بالا، قوانین حاکم بر سادهسازی ماتریس را توضیح میدهیم.
۱. تعویض دو ردیف
برای یک ماتریس میتوان بدون تغییر دادن ماهیت ضرایب ماتریسها، دو ردیف از ماتریس را با هم جابجا کرد. جابجا کردن ردیف ام و ام را به صورت نشان میدهند. برای نمونه ردیف اول و سوم ماتریس فوق را میتوان به صورت زیر جابجا کرد.
$$ \left [ {\begin {array} { r r r | r } 1 & { - 2 } & 3 & 7 \\ 2 & 1 & 1 & 4 \\ { - 3 } & 2 & { - 2 } & { - 10 } \end {array} } \right] \begin {array} {*{20} { c } } { { R _1 } \leftrightarrow { R _ 3 } } \\ \to \end{array}\left[ {\begin{array} { r r r | r } { - 3 } & 2 & { - 2 } & { - 10 } \\ 2 & 1& 1 & 4 \\ 1 & { - 2 } & 3 & 7 \end {array}} \right]$$
۲. ضرب یک سطر در عدد ثابت
بدیهی است که اگر یکی از معادلات در عددی ثابت ضرب شود، تاثیری در جواب نهایی معادلات دیده نمیشود؛ لذا میتوان گفت که با ضرب شدن یکی از سطرها در عددی ثابت نیز پاسخ نهایی بدست آمده برای متغیرها تغییر نمیکنند. برای نمونه با ضرب کردن سطر سوم در عدد ثابت ، ماتریس زیر بدست میآید.
$$ \large \left[ { \begin {array} { r r r | r } 1 & { - 2 } & 3 & 7 \\ 2 & 1 & 1 & 4 \\ { - 3 } & 2 & { - 2 } & { - 10 } \end {array}} \right] \begin {array} {*{20} { c } } { - 4 { R _ 3 } } \\ \to \end {array}\left[ {\begin{array} { r r r | r } 1 & { - 2 } & 3 & 7 \\ 2 & 1 & 1 & 4 \\ { 1 2} & { - 8 } & 8 & { 40 } \end {array}} \right] $$
۳. جمع کردن دو ردیف
ویژگی سوم ماتریس افزوده، تغییر نکردن پاسخ نهایی با جمع کردن دو ردیف و جایگزین کردن آن در یکی از ردیفها است. فرض کنید ردیف ام یک ماتریس با مضربی از ردیف ام جمع شوند. این عمل را میتوان به صورت زیر بیان کرد:
فرض کنید برای ماتریس ارائه شده در بالا، قصد داریم تا مضرب چهارم ردیف اول را از ردیف سوم کم کنیم. در این صورت ماتریس بهصورت زیر در خواهد آمد.
$$ \left[ {\begin {array} { r r r | r } 1 & { - 2 } & 3 & 7 \\ 2 & 1 & 1 & 4 \\ { - 3 } & 2 & { - 2 } & { - 10 } \end {array} } \right]\begin {array}{*{20} { c } } { { R _ 3 } - 4 { R _ 1 } \to { R _ 3 } } \\ \to \end {array} \left[ { \begin {array} { rrr|r}1&{ - 2 } & 3 & 7 \\ 2 & 1 & 1 & 4 \\ { - 7 } & { 10 } & { - 14 } & { - 38}\end{array}} \right] $$
جزئیات عملیات فوق در ادامه ارائه شدهاند.
حل دستگاه معادلات
حال با توجه به ویژگیهای بیان شده در بالا قصد داریم تا دستگاه دو معادله دو مجهول زیر را حل کنیم:
با توجه به مفاهیم بیانشده، ماتریس ضرایب برای معادله فوق را میتوان بهصورت زیر بیان کرد:
فرض کنید ماتریس فوق را به نحوی ساده کنیم که به ماتریس زیر برسیم.
در این صورت میتوان گفت و است. به این روش، سادهسازی گاوس-جردن گفته میشود. به مثالی که در ادامه ارائه شده، توجه فرمایید. بنابراین در این روش تلاش بر این است که ماتریس افزوده بهصورت ماتریس همانی در بیاید. در صورت همانی شدن ماتریس افزوده، ستون سمت راست را میتوان به عنوان پاسخ متغیرها در نظر گرفت. در ادامه دو مثال از سادهسازی به روش گاوس ارائه شده است.
مثال ۱
هریک از سیستمهای معادلات زیر را با استفاده از روش ماتریس افزوده حل کنید.
(a):
(b):
(c):
(a): در اولین قدم باید ماتریس افزوده متناسب با معادلات فوق را بدست آوریم. این ماتریس برابر است با:
$$ \large \require {color} \left [ { \begin {array} { r r | r } { \color {Red} 3 } & { - 2 } & { 14 } \\ 1 & 3 & 1 \end {array} } \right] $$
بهمنظور سادهسازی، از بالای ماتریس، سمت چپ شروع به نوشتن میکنیم؛ سپس به صورت پادساعتگرد حرکت کرده و تکتک اجزا ماتریس را آنگونه که باید باشد (مشابه با ماتریس همانی)، میسازیم. همانطور که میبینید عدد ۱ در ستون اول موجود است. از این رو سادهترین کار به عنوان قدم اول، جابجا کردن دو سطر با یکدیگر است.
$$ \large \require {color} \left[ { \begin {array} { r r | r } 3 & { - 2 } & { 1 4 } \\ 1 & 3 & 1 \end{array}} \right] \begin {array} {*{20} { c } } { { R _ 1 } \leftrightarrow { R _ 2 } } \\ \to \end{array} \left[ {\begin{array} { r r | r } 1 &<br /> 3 & 1 \\ { \color {Red} 3 } & { - 2 } & { 1 4 } \end{array} } \right] $$
با تغییر ساده فوق جزء اول برابر با ۱ بدست آمد. از این رو دیگر نباید به آن دست زد. در مرحله بعد هدف صفر کردن جزء پایین سمت چپ است. بدین منظور برابر ردیف اول را از ردیف دوم کم میکنیم. با انجام این کار داریم:
$$ \large \require{color} \left[ { \begin {array} { r r | r } 1 & 3 & 1 \\ 3 & { - 2 } & { 1 4 } \end {array} } \right] \begin {array}{*{20} {c }} { { R _ 2 } - 3{R_1} \to { R _ 2 } } \\ \to \end {array} \left[ {\begin {array}{rr|r} 1 & 3 & 1 \\ 0 & { \color {Red} - 11}&{ 11 } \end {array}} \right] $$
در گام بعد عدد سمت راست پایین باید صفر شود. بدین منظور کافی است ردیف پایین را به ۱۱- تقسیم کنیم. در ادامه این گام انجام شده است.
$$ \large \require{color}\left[ {\begin{array} { r r | r } 1 & 3 & 1 \\ 0 & { - 11 } & { 11 } \end {array}} \right] \begin {array} {*{20} { c } } { - \frac { 1 } { { 11 } } { R _ 2 } } \\ \to \end {array} \left[ {\begin {array} { r r | r } 1 & { \color {Red} 3 } & 1 \\ 0 & 1 & { - 1 } \end {array} } \right] $$
تنها یک گام بهمنظور رسیدن به ماتریس ایدهآل مانده و آن صفر کردن عدد بالا سمت راست است. بدین منظور ۳- برابر از ردیف پایین را با ردیف بالا جمع میکنیم. در نتیجه ماتریس نهایی برابر است با:
$$ \large \require {color} \left[ {\begin{array} { r r | r }1 & 3 & 1 \\ 0 & 1 & { - 1 } \end {array}} \right] \begin {array} {*{20}{c } } { { R _ 1 } - 3 { R _ 2 } \to { R _ 1 } } \\ \to \end {array} \left[ {\begin{array} { r r | r } 1 & 0 & 4 \\ 0 & 1 & { - 1}\end{array}} \right] $$
همانطور که میبینید ماتریس همانی بدست آمده است. بنابراین میتوان گفت مقادیر و برابرند با:
(b): دقیقا مشابه با روش بیانشده در بالا عمل کرده و ماتریس افزوده را به تدریج به ماتریس همانی تبدیل میکنیم. ستون اول را میتوان با دو عملیات بهشکل زیر مرتب کرد.
$$ \require {color} \left[ { \begin {array} { rr | r } { \color {Red} - 2 } & 1 & { - 3 } \\ 1 & { - 4 } & { - 2 } \end{array} } \right] \begin {array}{*{20} { c } }{ { R _ 1 } \leftrightarrow { R _ 2 } } \\ \to \end {array}\left[ {\begin{array} { r r | r } 1 & { - 4 } & { - 2 } \\ { \color {Red} - 2 } & 1 & { - 3}\end{array}} \right] \begin{array}{*{20 } { c } } { { R _ 2 } + 2 { R _ 1 } \to { R _ 2 } } \\ \to \end {array}\left[ {\begin{array} { r r | r }1 & { - 4 } & { - 2}\\0&{\color {Red} - 7 } & { - 7 } \end {array} } \right] $$
با استفاده از دو عملیات زیر نیز ستون سمت راست همانی خواهد شد. دو گام نهایی نیز بهصورت زیر خواهند بود.
$$\require {color} \left [ { \begin {array} { r r | r } 1 & { - 4 } & { - 2 } \\ 0 &{ \color {Red} - 7 } & { - 7 } \end {array}} \right]\begin {array}{*{20} { c } } { - \frac { 1 } { 7 } { R _ 2 } } \\ \to \end {array} \left[ { \begin{array} { r r | r } 1&{\color{Red} - 4 } & { - 2 } \\ 0 & 1 & 1 \end{array}} \right] \begin{array}{*{20}{c } } { {R _ 1 } + 4 { R _ 2 } \to {R_1}}\\ \to \end{array} \left[ {\begin{array}{rr|r}1 & 0 &2 \\ 0 & 1 & 1 \end{array}} \right]$$
بنابراین پاسخ سیستم معادلات برابر است با:
(c): ماتریس افزوده مربوط به این دستگاه برابر است با:
$$ \require {color} \left[ { \begin {array} { r r | r } { \color {Red} 3 } & { - 6 } & { - 9 } \\ { - 2 } & { - 2 } & { 12 } \end {array}} \right] $$
به نظر میرسد استفاده از روش گاوس-جردن برای این ماتریس اندکی مشکلتر بهنظر میرسد. ستون اول بهصورت زیر ساخته میشود.
$$ \require{color}\left[ {\begin{array} { r r | r } { \color{Red} 3}&{ - 6}&{ - 9 } \\ { - 2 } & { - 2 } & { 12 } \end {array} } \right]\begin{array}{*{20} { c } } { \frac {1 } { 3 } { R _1 } } \\ \to \end {array} \left[ {\begin{array} { r r | r } 1 & { - 2}&{ - 3 } \\ { \color {Red} - 2 } & { - 2}&{12}\end{array}} \right]\begin{array} {*{20}{c}}{{R_2} + 2 { R _ 1 } \to { R _ 2 } } \\ \to \end{array} \left[ { \begin{array}{rr|r}1&{ - 2}&{ - 3} \\ 0 & { \color {Red} - 6 } & 6 \end {array} } \right]$$
با استفاده از دو گام زیر نیز ستون دوم، مشابه با ماتریس همانی میشود.
$$ \large \require{color}\left[ {\begin{array}{rr|r}1 & { - 2 } & { - 3}\\0&{\color { Red } - 6}&6\end{array} } \right] \begin{array} {*{20} { c } } { - \frac{ 1 } { 6 } { R _ 2 } } \\ \to \end{array} \left[ {\begin{array}{rr|r} 1 & { \color{Red} - 2 } & { - 3}\\ 0 & 1 & { - 1 } \end {array}} \right]\begin {array} {*{20} { c } } { { R _ 1 } + 2{R_2} \to { R _ 1 } } \\ \to \end{array} \left[ {\begin {array}{rr|r}1&0&{ - 5}\\0&1&{ - 1 } \end {array}} \right] $$
بنابراین پاسخ این دستگاه نیز برابر است با:
نکته قابل توجه این است که روشهای مطرح شده در بالا تنها راه رسیدن به ماتریس همانی محسوب نمیشوند. بدیهی است که بهترین مسیر سادهسازی، مسیری است که کمترین میزان عملیات و البته زمان را نیاز داشته باشد. توجه داشته باشید که روش سادهسازی گاوس-جردن در مسائلی با سه یا مقادیر بیشتر مجهولات، بیشترین کاربرد را دارد. در دستگاهی با سه معادله و سه مجهول، هدف تبدیل ماتریس افزوده به ماتریسی به شکل زیر است.
در این صورت مقادیر ، و برابرند با:
مثال ۲
پاسخ هریک از سیستمهای زیر را بیابید.
(a):
(b):
(a): ماتریس افزوده برای این دستگاه معادلات برابر است با:
$$ \require {color} \left [ { \begin {array} { r r r | r } { \color {Red} 3 } & 1 & { - 2 } & 2 \\ 1 & { - 2 } & 1 & 3 \\ 2 & { - 1}&{ - 3 } & 3 \end {array}} \right] $$
توجه داشته باشید که در هر مرحله، هدف تغییر اعداد قرمز است. در ابتدا ستون اول را میسازیم. بدین منظور داریم:
$$ \require {color} \left[ { \begin {array} { r r r | r } { \color { Red } 3 } & 1 & { - 2 } & 2 \\ 1 & { - 2 } & 1 & 3 \\ 2 & { - 1 } & { - 3 } & 3 \end{array}} \right]\begin{array} {*{20} { c } } { { R _ 1} \leftrightarrow {R_2}}\\ \to \end{array}\left[ {\begin {array} { r r r | r } 1 & { - 2 } & 1 & 3 \\ {\color {Red} 3 } & 1 & { - 2 } & 2 \\ { \color {Red} 2 } & { - 1} & { - 3 } & 3 \end{array}} \right]$$
با استفاده از دو گام زیر، اعداد قرار گرفته در ستون اول نیز صفر خواهند شد (اعداد قرار گرفته زیر ۱).
$$ \require {color} \left [ {\begin{array} {rrr|r}1&{ - 2}&1&3\\{\color{Red} 3}&1&{ - 2}&2\\{\color {Red} 2 } & { - 1 } & { - 3}&3\end{array}} \right]\begin{array}{*{20} { c } } { { R _ 2 } - 3 { R _ 1 } \to { R _ 2 }} \\ { { R _ 3} - 2{R_1} \to { R _ 3 } } \\ \to \end{array}\left[ { \begin{array} { r r r | r }1&{ - 2 } & 1 & 3 \\ 0 & { \color {Red} 7}&{ - 5}&{ - 7 } \\ 0 & 3 & { - 5 } & { - 3 } \end {array}} \right]$$
تا الان ستون اول ساخته شده است. در مرحله بعد عدد مورد نیاز در ستون دوم را میسازیم.
$$ \require {color} \left [ { \begin {array} { r r r | r } 1 & { - 2 } & 1 & 3 \\ 0 & { \color { Red } 7 } & { - 5 } & { - 7 } \\ 0 & 3 & { - 5 } & { - 3 } \end {array}} \right] \begin {array} {*{20} { c } } { \frac { 1 } { 7 } { R _ 2 } } \\ \to \end{array}\left[ { \begin{array} { r r r | r } 1 & { - 2 } & 1 & 3 \\ 0 & 1 & { - \frac{5}{7}}&{ - 1}\\0&{ \color {Red} 3 } & { - 5 } & { - 3 } \end {array}} \right]$$
در گام بعد عدد ستون دوم و ردیف سوم را مطابق با گامهای زیر به صفر تبدیل میکنیم.
$$ \require {color} \left [ { \begin {array} { r r r | r } 1 & { - 2 } & 1 & 3 \\ 0<br /> & 1 & { - \frac { 5 } {7 } } & { - 1 } \\ 0 & { \color {Red} 3 } & { - 5 } & { - 3 } \end {array}} \right]\begin{array}{*{20} { c } } { { R _ 3 } - 3 { R _ 2 } \to { R _ 3 } } \\ \to \end {array} \left[ {\begin{array} { r r r | r }1 & { - 2} & 1 &3 \\ 0 & 1&{ - \frac { 5 } { 7 } } & { - 1}\\ 0 & 0 & {\color{Red} - \frac { { 2 0} } { 7} } & 0 \end {array}} \right]$$
آخرین عدد مورد نیاز در ردیف و ستون سوم با استفاده از گامهای زیر بدست میآید.
$$ \require {color} \left [ {\begin {array} { r r r |r } 1 & { - 2 } & 1 & 3 \\<br /> 0 & 1 & { - \frac { 5 } { 7 } } & { - 1 } \\ 0 & 0 & {\color{Red} - \frac { { 20 } } { 7 } } & 0 \end{array} } \right] \begin{array}{*{20} { c } } { - \frac { 7 } { { 2 0 } }{R_3}}\\ \to \end{array}\left[ {\begin{array} { r r r | r } 1 & { - 2}&{\color{Red} 1 } & 3 \\ 0 & 1 & {\color {Red} - \frac { 5 } { 7 } } & { - 1 } \\ 0 & 0 & 1 & 0 \end{array}} \right] $$
تا این مرحله اعداد روی قطر اصلی و اعداد قرار گرفته زیر آن، مشابه با ماتریس همانی شدهاند. اما همانطور که مشاهده میکنید اعداد بالای قطر اصلی غیر صفر هستند. با استفاده از دو قدم زیر، اعداد ستون سوم را صفر میکنیم.
$$ \require {color} \left [ { \begin {array} { r r r | r } 1 & { - 2 } & { \color { R e d } 1 } & 3 \\ 0 & 1 & { \color { R e d } - \frac { 5 } { 7 } } & { - 1 } \\ 0 & 0 & 1 & 0 \end {array}} \right] \begin {array} {*{20} { c } } { { R _ 2 } + \frac { 5 } { 7 }{ R _ 3 } \to { R _2 } } \\ { { R _ 1 } - { R _ 3 } \to { R _ 1 } } \\ \to \end {array} \left[ { \begin {array} { r r r | r }1 & { \color { R e d } - 2 } & 0 & 3 \\ 0 & 1 & 0 & { - 1} \\ 0 & 0 & 1 & 0 \end {array}} \right]$$
در قدم آخر نیز عدد قرار گرفته در ستون دوم و ردیف اول را صفر میکنیم. بدین منظور ردیف اول را با دوبرابر ردیف دوم جمع میکنیم. با انجام این گام داریم:
$$ \require {color} \left[ { \begin {array} { r r r |r } 1 & { \color { R e d } - 2 } & 0 & 3 \\ 0 & 1 & 0 & { - 1 } \\ 0 & 0 & 1 & 0 \end{array}} \right]\begin{array}{*{20}{ c } } { {R _ 1 } + 2 { R _ 2 } \to { R _ 1 } } \\ \to \end {array} \left[ { \begin{array} { r r r | r } 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & { - 1 } \\ 0 &0 & 1& 0 \end{array}} \right]$$
همانطور که مشاهده میکنید با انجام گامهای فوق، ماتریس همانی بدست میآید. در نتیجه مقادیر متغیرها برابرند با:
بهمنظور اطمینان حاصل کردن از درست بودن پاسخ، میتوانید اعداد بدست آمده را در معادلات قرار دهید.
(b): دقیقا مشابه با حالت a، ماتریس افزوده را بهصورت زیر بیان میکنیم:
$$ \require{color}\left[ {\begin{array} { r r r | r } { \color { R e d } 3 } & 1 & { - 2 } & { - 7 } \\ 2 & 2 & 1 & 9 \\ { - 1 } & { - 1 } & 3 & 6 \end {array}} \right] $$
توجه داشته باشید که در استفاده از روش گاوس-جردن در هر مرحله باید مسیری طی شود که در آن کمترین عملیات ممکن احتیاج باشد. برای نمونه در ماتریس فوق میتوان ردیف دوم و اول را با هم جابجا کرد؛ اما این مسیر نیاز به دو عملیات دارد. با کم کردن ردیف دوم از ردیف اول، عدد ۳ به ۱ تبدیل خواهد شد. در ادامه این گام انجام شده است.
$$ \require {color} \left [ { \begin {array} { r r r | r } { \color { R e d } 3}&1&{ - 2} & { - 7 } \\ 2 & 2 & 1 & 9 \\ { - 1 } & { - 1 } & 3 & 6\end{array} } \right] \begin{array} {*{20} { c } }{ { R _1 } - { R _ 2 } \to { R _ 1 } } \\ \to \end {array} \left[ {\begin {array}{rrr|r} 1 & { - 1 } & { - 3 } & { - 16 } \\{\color{Red} 2 } & 2 & 1 & 9 \\ { \color{Red} - 1}&{ - 1 } & 3 & 6 \end {array}} \right]$$
دو مولفه دیگر ستون اول نیز مطابق با دو گام زیر صفر میشوند.
$$ \require {color}\left[ { \begin{array}{rrr|r} 1 & { - 1 } & { - 3 } & { - 16 } \\ { \color { R e d } 2 } & 2 &1 & 9 \\ { \color { R e d } - 1 } & { - 1} & 3 & 6 \end {array}} \right]\begin {array}{*{20}{c} } { { R _ 2 } - 2{R_1} \to { R _ 2 } } \\ { { R _ 3 } + { R _ 1 } \to { R _ 3 } } \\ \to \end {array}\left[ {\begin{array} {rrr|r} 1 & { - 1}&{ - 3}&{ - 1 6 } \\ 0 & { \color {Red} 4 } & 7 &{ 41 } \\ 0 & { - 2 } & 0 & { - 10}\end{array}} \right] $$
در قدم بعدی با تقسیم کردن ستون دوم به عدد ۲- دیگر مولفه قطر اصلی بدست خواهد آمد.
$$ \require {color} \left [ { \begin {array} { r r r | r } 1 & { - 1 } & { - 3 } & { - 16 } \\ 0 & { \color {Red} - 2 } & 0 & { - 10}\\ 0 & 4 & 7 & { 41} \end{array}} \right]\begin{array}{*{20}{ c } } { - \frac { 1 } { 2 } { R _ 2 } } \\ \to \end {array} \left[ {\begin{array} { r r r | r } 1 & { - 1 } & { - 3}&{ - 16 } \\ 0 & 1 & 0 & 5 \\ 0 & {\color{Red} 4 } & 7 & { 41 } \end{array}} \right] $$
قبل از ارائه ادامه حل توجه به دو نکته مهم است. اولین نکته این است که حتیالامکان از ایجاد کسر در ماتریس جلوگیری شده است. برای نمونه در گام اول میتوانستیم تمامی اعداد را به ۳ تقسیم کنیم. اما با انجام این کار دیگر مولفهها بهصورت کسری در خواهند آمد. نکته دوم این است که در مواردی ممکن است بتوان تنها با یک گام دو یا چند مولفه را بهصورت مولفههای ماتریس همانی بدست آورد. در قدم بعدی مولفههای قرار گرفته در زیر قطر اصلی را صفر میکنیم. با استفاده از گام ارائه شده در ادامه، مولفه سطر سوم و ستون دوم صفر میشوند.
$$ \require {color} \left [ { \begin {array} { r r r |r } 1 & { - 1 } & { - 3 } & { - 16 } \\ 0 & 1 & 0 & 5 \\ 0 & { \color { Red } 4 } & 7 & { 41 } \end {array}} \right] \begin {array} {*{20} {c } } { { R _ 3 } - 4 { R _ 2 } \to { R _ 3 } } \\ \to \end {array} \left[ {\begin{array}{rrr|r}1&{ - 1}&{ - 3}&{ - 16 } \\ 0 & 1& 0 & 5 \\ 0 & 0 & { \color {Red} 7} & {21}\end{array}} \right] $$
مولفههای غیر قطری سطر سوم برابر با صفر هستند. بنابراین میتوان بهمنظور بدست ۱ کردن عدد روی قطر آن را به ۷ تقسیم کرد. با انجام این گام، ماتریس بهصورت زیر در خواهد آمد.
$$ \require {color} \left [ { \begin {array} { r r r | r } 1 & { - 1 } & { - 3 } & { - 16 } \\ 0 & 1 & 0 & 5 \\ 0 & 0 & { \color {Red} 7 } & { 21 } \end {array} } \right] \begin {array} {*{20} { c } } { \frac { 1 } { 7 }{ R _ 3 } } \\ \to \end {array} \left [ { \begin {array} { r r r | r }1 & { - 1 } & { \color {Red} - 3 }& { - 16 } \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \end{array}} \right]$$
در دو گام نهایی نیز دو مولفه غیر قطری سطر اول برابر با صفر میشوند:
$$ \require {color} \left [ { \begin {array} { r r r | r } 1 & { - 1 } & { \color {Red} - 3 } & { - 16 } \\ 0 & 1 & 0 & 5 \\ 0 & 0 &1 & 3 \end {array}} \right]\begin{array}{*{20} { c} } { { R _ 1 } + 3{R_3} \to { R _ {\kern 1pt} }}\\ \to \end{array}\left[ {\begin{array}{ r r r |r } 1 & { \color {Red} - 1} & 0 & { - 7} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \end {array}} \right] $$
$$ \require {color} \left [ { \begin {array} { r r r | r } 1 & { \color {Red} - 1 } & 0 &{ - 7} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \end{array}} \right]\begin {array}{*{20} { c } } { { R _ 1 } + { R _ 2 } \to {R_{\kern 1pt} } } \\ \to \end{array}\left[ {\begin{array} {rrr|r} 1 & 0 & 0 & { - 2} \\ 0 & 1 & 0 & 5 \\0 & 0 &1 & 3 \end {array}} \right]$$
بنابراین میتوان گفت پاسخها برابرند با:
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضی و فیزیک
- مجموعه آموزشهای ریاضی
- دترمینان یک ماتریس — به زبان ساده
- ضرب ماتریسها – به زبان ساده
- معکوس ماتریس یا ماتریس وارون – به زبان ساده
^^













واقعا عالی، مرسی خیلی کمکم کرد
عالی دمت گرم