فرادرس
فنر پیچشی — به زبان ساده
در مطالب گذشته وبلاگ فرادرس در مورد انواع تنش‌ها صحبت شد. در این مطلب قصد داریم تا مشخصا در مورد فنر پیچشی صحبت کرده و تنش‌های برشی و قائم ایجاد شده در آن را در نتیجه تغییر شکلِ فنر بدست آوریم. البته مطالعه نوشته‌های تنش برشی و کرنش برشی و پیچش و تنش برشی نیز خالی از لطف نخواهند بود.
فنر پیچشی
فنر پیچشی، از سیمی به قطر $$ d $$ تشکیل شده که به صورت مارپیچی و مطابق با شکل زیر پیچیده شده است.
در نتیجه نهایتا استوانه‌ای به شعاع $$ R $$ بدست می‌آید. اگر مطابق با شکل زیر به این فنر نیرویی برابر با $$ P $$ وارد شود، در این صورت تنش‌هایی برشی و قائم در آن ایجاد خواهند شد.
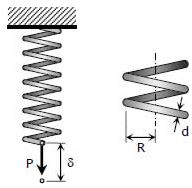
بیشترین تنش برشی ایجاد شده برابر با مجموع تنش برشی مستقیم ایجاد شده در فنر و تنش برشی پیچشی است. این تنش‌ها برابرند با:
$$ \large \tau _ 1 = \frac { P } { A } \ , \ \tau _ 2 = \frac { T r } { J } $$
در رابطه فوق $$ \tau _ 1 $$ و $$ \tau _ 2 $$ به ترتیب نشان‌دهنده تنش‌های برشی مستقیم و پیچشی هستند. هم‌چنین $$ T $$ نشان‌دهنده گشتاور پیچشی وارد شده به فنر و برابر با $$ T = P R $$ است. توجه داشته باشید که اندازه تنش قائم نیز برابر است با:
$$ \large \tau _ 1 = \frac { P } { A } $$
تنش برشی ماکزیمم در نتیجه اعمال نیروی $$ P $$ به فنر برابر است با:
$$ \large \tau = \dfrac { P } { \pi d ^ 2 / 4 } + \dfrac { 16 P R } { \pi d ^ 3 } $$
نهایتا با جمع زدن رابطه فوق، اندازه تنش برشی ماکزیمم برابر می‌شود با:
$$ \large \boxed { \tau = \dfrac { 16 P R } { \pi d ^ 3 } \left ( 1 + \dfrac { d } { 4 R } \right ) } $$
توجه داشته باشید که روابط فوق برای حالتی نوشته شده که در آن از خمیدگیِ فنر صرف نظر شده باشد. در حقیقت در این حالت نسبتِ $$ \frac { d } { 4 R } $$ به اندازه کافی کوچک در نظر گرفته شده است. البته در حالتی که خمیدگی فنر نیز در نظر گرفته شده باشد، تنش برشی ایجاد شده در فنر را می‌توان مطابق با رابطه زیر بدست آورد.
$$ \large \tau = \dfrac { 16 P R } { \pi d ^ 3 } \left ( \dfrac { 4 m - 1 }{ 4 m - 4 } + \dfrac { 0.615 } { m } \right ) $$
در رابطه فوق $$ m = \frac { 2 R } { d } $$، شاخص فنر است. هم‌چنین تغییر طول فنر در نتیجه وارد شدن نیروی $$P$$ به آن نیز مطابق با رابطه زیر بدست می‌آید.
$$ \large \delta = \dfrac { 64 P R ^ 3 n } { G d ^ 4 } $$
معادله ۱
رابطه فوق نشان می‌دهد که تغییر طولِ $$ \delta $$ به صورت مستقیم با نیروی $$ P $$ تغییر می‌کند؛ بنابراین سختی معادل فنر را می‌توان مطابق با رابطه زیر بدست آورد.
$$ \large k = \dfrac { P } { \delta } = \dfrac { G d ^ 4 } { 64 R ^ 3 n } \, \text { N/mm } $$
فنر‌های سری
مطابق با شکل زیر دو یا چند فنر را در نظر بگیرید که به صورت سری به یکدیگر متصل شدهاند.
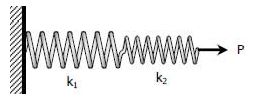
در این صورت ثابتِ معادل فنر برابر است با:
$$ \large 1 / k = 1 / k _ 1 + 1 / k _ 2 + \dots $$
در رابطه فوق، $$ k _ 1 , k _ 2 , ... $$ ثابت‌های فنر هستند.
فنر‌های موازی
حالتی را در نظر بگیرید که دو یا چند فنر به صورت موازی، مطابق با شکل زیر به هم بسته شدهاند.
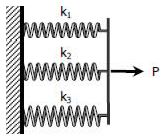
در این حالت سختی فنر افزایش می‌یابد. در حقیقت سختی معادل فنر در این حالت برابر است با:
$$ \large k = k _1 + k _ 2 + \dots $$
در ادامه مثال‌هایی ذکر شده که به منظور درک بهتر مطلب، پیشنهاد می‌شود آن‌ها را مطالعه فرمایید.
مثال ۱
همانطور که در شکل زیر نیز نشان داده شده، تیری به جرم $$50 $$ کیلوگرم به $$ 3 $$ سه فنر متصل شده است. دو فنر سمت چپ از جنس فولاد بوده و فنر سمت راست نیز از برنز ساخته شده است. هریک از فنر‌های فولادی از $$24$$ دور مفتول با قطر $$10 \ mm$$ تشکیل شدهاند. هم‌چنین قطر حلقه‌های ایجاد شده فنر و مدول برشی فولاد به ترتیب برابر با $$100 \ mm$$ و $$ G = 83 G P a $$ هستند. این در حالی است که فنر برنزی از $$48$$ دور مفتول با قطرِ $$20mm$$ و با مدول برشی $$ G = 42 G P a $$ تشکیل شده است. هم‌چنین قطر فنر برنزی ایجاد شده برابر با $$150 mm$$ است. با این فرضیات، تنش برشی ماکزیمم ایجاد شده در هریک از فنر‌ها را بیابید.
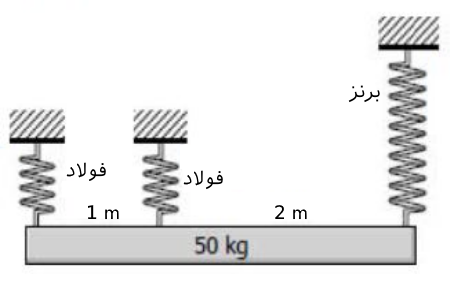
در اولین قدم باید نیرو‌های کششی ایجاد شده در هریک از فنر‌ها را بیابید. بدین منظور با فرض کردن تیر به عنوان سیستم و نماد‌گذاری $$ P _ 1 , P _ 2 , P _ 3 $$ به عنوان نیرو‌های موجود در فنر‌ها، معادله تعادل نیرویی در راستای $$ y $$ به صورت زیر نوشته می‌شود:
$$ \Sigma F _ V = 0 $$
$$ P _ 1 + P _ 2 + P _ 3 = 490.5$$
معادله ۲
معادله بعدی نیز با محاسبه تعادل گشتاوری حول نقطه ۱ برابر می‌شود با:
$$ \Sigma M _ 1 = 0 $$
$$ P _ 2 ( 1 ) + P _ 3 ( 3 ) = 490.5 (1.5) $$
$$ P _ 2 + 3 P _ 3 = 735.75 $$
معادله ۳
در شکل زیر نیرو‌های وارد شده و تغییرات شکل ایجاد شده در فنر‌ها نشان داده شدهاند.
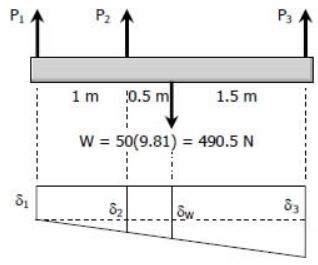
همانطور که می‌دانید به منظور یافتن نیرو‌ها به $$3$$ معادله نیاز است. تاکنون دو معادله نوشته شده است. معادله سوم را می‌توان با استفاده از تغییر شکل بیان کرد. بدین منظور در اولین قدم با استفاده از قضیه تالس می‌توان رابطه زیر را بین تغییر شکل‌های فنر بیان کرد:
$$ \large \dfrac { \delta _ 2 - \delta _ 1 } { 1 } = \dfrac { \delta _ 3 - \delta _ 1 }{ 3 } $$
$$ \large \delta _ 2 = \frac { 1 } { 3 } \delta _ 3 + \frac { 2 } { 3 } \delta _ 1 $$
با استفاده از معادله $$1$$ و جایگذاری مقادیر نیرو و مدول برشی در آن به روابط زیر خواهیم رسید.
$$ \large \dfrac { 64 P _ 2 ( 50 ^ 3 ) ( 24 ) } { 83\,000 ( 10 ^ 4 ) } = \dfrac { 1 } { 3 } \left[ \dfrac { 64 P _ 3 ( 75 ^ 3 ) ( 4 8 ) }{ 42 \, 000 ( 20 ^ 4 ) } \right] + \dfrac { 2 } { 3 } \left[ \dfrac { 64 P _ 1 ( 50 ^ 3 )( 2 4 ) } { 83\,000( 10 ^ 4 ) } \right] $$
$$ \large \frac { 3 } { 830 } P _ 2 = \frac { 9 } { 8960 } P _ 3 + \frac { 1 }{ 415 } P _ 1 $$
$$\Rightarrow \large \frac { 3 } { 166 } P _ 2 = \frac { 9 } { 1792 } P _ 3 + \frac { 1 }{ 83 } P _ 1 $$
$$\Rightarrow \large \frac { 3 } { 166 } P _ 2 = \frac {9} { 1792 } P _ 3 + \frac { 1 } { 83 } P _ 1 $$
معادله ۴
حال معادله ۲ را به صورت زیر بازنویسی می‌کنیم.
$$ \large P _ 1 = 490.5 - P _ 2 - P _ 3 $$
با قرار دادن مقدار $$ P _ 1 $$ در معادله ۴، داریم:
$$ \large \frac { 3 } { 166 } P _ 2 = \frac { 9 } { 1792 } P _ 3 + \frac { 1 } { 83 }( 490.5 - P _ 2 - P _ 3 ) $$
معادله ۵
هم‌چنین معادله ۳ را به شکل زیر بازنویسی می‌کنیم.
$$ \large P _ 2 = 735.75 - 3 P _ 3 = \frac { 2943 } { 4 } - 3 P _ 3 $$
با قرار دادن عبارت فوق در معادله ۵، مقادیر $$ P $$ برابرند با:
$$ \large \frac { 5 } { 166 } ( \frac { 2943 } { 4 } - 3 P _ 3 ) = \frac { 981 } { 166 } - \frac { 1045 } { 148\,736} P _ 3 ) $$
$$ \large ( \frac { 1045 } { 148\,736} - \frac { 5 } { 166 } ) P _ 3 = \frac { 981 }{ 166 } - \frac { 14\,715 } { 664 } $$
با بدست آمدن مقادیر $$ P $$ کافی است آن‌ها را در رابطه تنش ماکزیمم قرار داده و مقدار تنش برشی ماکزیمم را بدست آورد.
$$ \large \tau _ { m a x } = \dfrac { 16 P R } { \pi d ^ 3 } \left ( 1 + \dfrac { d }{ 4 R } \right ) $$
برای فنر‌های فولادی سمتِ چپ مقادیر تنش ماکزیمم برابرند با:
$$ \large \tau _ { m a x 1 } = \dfrac { 16 ( 144.77 ) ( 50 ) } { \pi ( 10 ^ 3 ) } \left[ 1 + \dfrac { 10 } { 4 ( 50 ) } \right] = 38.709 \, \text{ MPa } $$
$$ \large \tau _ { m a x 2 } = \dfrac { 16 ( 150.72 ) ( 50 ) } { \pi ( 10 ^ 3 ) } \left[ 1 + \dfrac { 10 } { 4 ( 50 ) } \right] = 40.300 \, \text{ MPa} $$
تنش برشی ماکزیمم در فنر برنزی نیز برابر با مقدار زیر بدست می‌آید.
$$ \large \tau _ { m a x 3 } = \dfrac { 16 ( 195.01 ) ( 75 ) } { \pi ( 20 ^ 3 ) } \left[ 1 + \dfrac { 20 } { 4 ( 75 ) } \right] = 9.932 \, \text{ MPa } $$
توجه داشته باشید که در محاسبه تنش‌های فوق، هم تنش‌های نرمال و هم تنش‌های ناشی از پیچش در نظر گرفته شدهاند.
مثال ۲
تیری صلب را در نظر بگیرید که در یک سمت پین شده است. این تیر از دو سمت دیگر به دو فنر پیچشی متصل شده است. فرض کنید هر فنر دارای $$20$$ حلقه مفتول به قطرِ $$10mm$$ بوده و نهایتا قطرِ کلی فنر تولید شده برابر با $$150 mm$$ باشد. با فرض بی‌وزن بودنِ تیر، ماکزیمم تنش برشی ایجاد شده در فنر را بدست آورید.
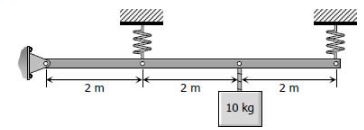
سیستم فوق در حالت تعادلش به صورت زیر در خواهد آمد.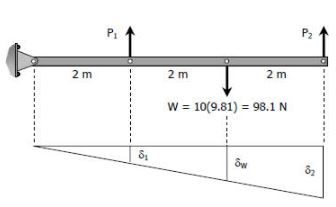
بنابراین قضیه تالس را برای سیستم فوق می‌توان به صورت زیر بیان کرد:
$$ \large \dfrac { \delta _ 1 } { 2 } = \dfrac { \delta _ 2 } { 6 } $$
$$ \large \delta _ 1 = \frac { 1 } { 3 } \delta _ 2 $$
حال با جایگذاری رابطه تغییر طول در عبارات فوق، داریم:
$$ \large \dfrac { 64 P _ 1 R ^ 3 n } { G d ^ 4 } = \dfrac { 1 } { 3 } \left ( \dfrac { 64 P _ 2 R ^ 3 n } { G d ^ 4 } \right ) $$
$$ \large P _ 1 = \frac { 1 } { 3 } P _ 2 $$
رابطه دوم بین نیرو‌ها را می‌توان با گشتاورگیری حول لولای مرکز بدست آورد. با محاسبه گشتاور حول نقطه مذکور داریم:
$$ \large \Sigma M _ { a t \,\,hinged \,\,support } = 0 $$
$$ \large 2 P _ 1 + 6 P _ 2 = 4 ( 98.1 ) $$
$$ \large 2 ( \frac { 1 } { 3 } P _ 2 ) + 6 P _ 2 = 4 ( 98 . 1 ) $$
بنابراین اندازه نیرو‌ها برابرند با:
$$ \large P _ 2 = 5 8 .8 6 \, \text{N} $$
در نتیجه برای فنر سمت چپ، اندازه تنش ماکزیمم برابر است با:
$$ \large \tau _ { max 1 } = \dfrac { 16 ( 19.62 ) ( 75 ) } { \pi ( 10 ^ 3 ) } \left[ 1 + \dfrac { 10 } { 4(75 ) } \right]$$
$$ \large \tau _ { max 1 } = 7.744 \, \text{MPa} $$
به همین صورت، تنش ماکزیمم در فنر سمت راست نیز برابر با مقدار زیر بدست می‌آید.
$$ \large \tau _ { max 2 } = \dfrac { 16 ( 58.86 ) ( 7 5 ) } { \pi ( 1 0^ 3 ) } \left[ 1 + \dfrac { 10 } { 4 ( 75 ) } \right] $$
$$ \large \tau _ {m a x 2 } = 23.232 \, \text { MPa} $$
مثال ۳
دو فنر فولادی که به صورت سری به هم متصل شدهاند در شکل زیر نشان داده شده است.
فرض کنید به این مجموعه نیروی $$ P $$ مطابق با شکلِ فوق وارد شود. فنر بالاتر دارای $$ 12 $$ دور مفتول با قطر $$ 25 \ mm $$ بوده و قطر فنر تولید شده نیز برابر با $$100 mm$$ است. فنر پایین‌تر نیز از $$ 10 $$ دور مفتول با قطر $$ 20 \ mm $$ تشکیل شده و قطر فنر نیز برابر با $$75 mm$$ است. با فرض این‌که تنش تسلیم فولاد برابر با $$ G = 83 \ G P a $$ باشد و بدون صرف نظر از اثرات خمش، بیشترین نیروی قابل اعمالِ $$ P $$ و هم‌چنین تغییر طولِ فنر در نتیجه این نیرو را بیابید.
همانطور که عنوان شد تنش برشی ماکزیمم با استفاده از رابطه زیر بدست می‌آید.
$$ \large \tau _ { max } = \dfrac { 16 P R } { \pi d ^ 3 } \left ( \dfrac { 4 m - 1 } { 4 m - 4 } + \dfrac {0.615} { m } \right ) $$
کافی است در هریک از فنر‌ها تنش تسلیم را برابر با تنش برشی ماکزیمم قرار داد. با انجام این کار برای فنر اول داریم:
$$ \large 200 = \dfrac { 16 P ( 100 ) } { \pi ( 25 ^ 3 ) } \left[ \dfrac { 4 ( 8 ) - 1 } { 4 ( 8 ) - 4 } + \dfrac {0.615} { 8 } \right] $$
$$ P = 5182.29 \, \text {N} $$
به همین صورت برای فنر دوم نیز می‌توان نوشت:
$$ \large 200 = \dfrac { 1 6 P ( 7 5 ) } { \pi ( 20^ 3) } \left[ \dfrac { 4 ( 7 .5) - 1} { 4 ( 7.5 ) - 4 } + \dfrac {0.615} {7.5} \right] $$
$$ \large P = 3498.28 \, \text { N } $$
از بین نیرو‌های بدست آمده در بالا، نیروی کمتر به عنوان پاسخ در نظر گرفته می‌شود. بنابراین پاسخ قابل قبول برابر با نیروی زیر است.
$$ \large P = 3498.28 \, \text{N} $$
توجه داشته باشید که مقدار $$ d $$ نیز دو برابر نسبت قطر فنر به قطر مفتول است. برای محاسبه تغییر طول نیز کافی است تغییر طول هریک را بدست آورده و با هم جمع کنید. بنابراین تغییر طول فنر برابر می‌شود با:
$$ \large \delta = \delta _ 1 + \delta _ 2 $$
$$ \large \delta = \left ( \dfrac { 64P R^ 3 n } { G d ^ 4 } \right ) _ 1 + \left ( \dfrac { 6 4 P R^ 3 n } { G d ^ 4 } \right ) _ 2 $$
tt$$ \large \delta = 153.99 \, \text { mm} $$
جالب است بدانید که با محاسبه تغییر شکل فنر و داشتن نیروی وارد به آن می‌توانیم سختی معادل را به صورت زیر بدست آوریم:
$$ k _ { equivalent } = \dfrac { P } { \delta } = \dfrac { 3498.28 } { 153.99 } $$
^^
