فرمول دلتا و روش دلتا برای حل معادله درجه ۲ – به زبان ساده

فرمول دلتا و روش دلتا یکی از مهم‌ترین فرمول‌هایی است که از آن برای یافتن جواب‌های معادله درجه 2 استفاده می‌شود. در این آموزش با فرمول دلتا و روش دلتا برای حل معادلات درجه 2 آشنا می‌شویم.

معادله چیست؟

در ریاضیات، معادله را می‌توان به‌عنوان یک عبارت ریاضی متشکل از یک نمادِ مساوی بین دو عبارت جبری که دارای مقدار یکسان هستند، تعریف کرد. به زبان ساده‌تر، معادله یک تساوی بین دو عبارت جبری است.

ابتدایی‌ترین و رایج‌ترین معادلات جبری در ریاضیات از یک یا چند متغیر تشکیل شده است. به‌عنوان مثال، $$3 x + 5 = 14$$ معادله‌ای است که در آن، $$3 x + 5$$ و $$14$$ دو عبارتی هستند که با علامت «مساوی» یا "=" از هم جدا شده‌اند. در یک معادله جبری، سمت چپ با سمت راست برابر است.

در اینجا، برای مثال، $$5x + 9$$ عبارت سمت چپ است که برابر است با عبارت $$24$$ در سمت راست.

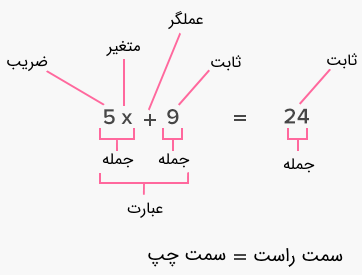
برای مثال، $$2x + 17y – 3$$ یک معادله نیست، زیرا علامت تساوی ندارد و فقط یک عبارت است. مطالعه جبر عمدتاً در مورد یادگیری حل انواع مختلف معادلات است.

حل معادله چیست؟

فرایند یافتن مقدار متغیر را معادله را حل معادله می‌گویند. معادله، بسته به نوعش، می‌تواند تعداد صفر تا بی‌نهایت جواب داشته باشد.

معادله درجه 2 چیست؟

«معادله درجه دوم» (Quadratic Equation) معادله‌ای است که یک متغیر با توان 2 به‌عنوان بزرگ‌ترین جمله توان‌دار دارد. برای مثال، معادله زیر مرتبه دوم است:

$$\large 3 x ^ 2 - 5 x - 2 = 0$$

در معادله بالا، داریم:

• $$x$$ متغیر است که عددی را با مقدار مجهول نشان می‌دهد.
• $$... ^ 2$$ توان یا نما است. نمای $$2$$ یعنی اینکه متغیر در خودش ضرب شده است.
• $$3$$ و $$-5$$ ضرایب هستند.
• $$-2$$ یک جمله ثابت است.

حل معادله درجه 2 در حالت‌های خاص

روش‌های مختلفی برای حل معادله درجه 2 وجود دارد که برخی از آن‌ها، با توجه به نوع و شرایط معادله، راه‌حل‌های خاصی دارند. در ادامه، به حالت‌های خاص اشاره کوتاهی می‌کنیم و سپس فرمول دلتا را برای حل معادله درجه 2 بیان خواهیم کرد.

حل معادله درجه 2 بدون x

معادله‌های درجه دومی که بدون جمله $$x$$ هستند، مانند $$2 x ^ 2 = 32$$ را می‌توان بدون قرار دادن یک عبارت درجه دوم با $$0$$ حل کرد. در عوض، می‌توانیم از $$x ^ 2$$ با ضریب 1، جذر یا رادیکال بگیریم و با عملیات ساده‌ای، $$x$$ را به‌دست آوریم.

هنگام حل معادلات درجه دوم با روش جذر گرفتن، هردو ریشه مثبت و منفی جواب معادله هستند. دلیل این امر آن است که وقتی یک جواب را به توان 2 می‌رسانیم، نتیجه همیشه مثبت است.

برای مثال، برای معادله $$x ^ 2 = 4$$، جواب‌ها $$-2$$ و $$2$$ هستند:

• $$2 ^ 2 = 4$$
• $$(-2)^ 2 = 4$$

برای حل معادلات مرتبه دومی که جملات شامل $$x$$ ندارند، دو کار زیر را انجام می‌دهیم:

1. ضریب $$x^2$$ را با ضرب یا تقسیم طرفین معادله بر ضریب آن، به $$1$$ تبدیل می‌کنیم.
2. جذر دو طرف معادله را می‌گیریم. هر دو جذر مثبت و منفی جواب هستند.

مثال ۱: مقدار $$x$$ را از معادله $$2 x ^ 2 = 18$$ به‌دست آورید.

حل: مقدار $$x$$ به‌صورت زیر به دست می‌آید:

$$\large \begin {aligned} 2 x ^ 2 & = 18 \\ \dfrac { 2 x ^ 2 }{ { 2 } } & = \dfrac { 1 8 } { { 2 } } \\ x ^ 2 & = 9 \\ { \sqrt { { x ^ 2 } } } & = { \sqrt { { 9 } } } \\ x&= \pm 3 \end {aligned}$$

مقادیر $$x$$ را از معادله $$2 x ^ 2 = 18$$ به‌‌صورت زیر خواهند بود:

$$-3$$ و $$3$$

مثال: معادله $$x ^ 2 - 3 = 13$$ را حل کنید.

حل: ابتدا عدد $$3$$ را به دو سمت معادله اضافه می‌کنیم و خواهیم داشت:

$$\begin{aligned} x ^ 2 - 3 &= 13 \\ x ^ 2 - 3 { + 3 } & = 13 { + 3 } \\ x ^ 2 & = 1 6 \end{aligned}$$

می‌بینیم که ضریب $$x ^ 2$$ برابر با $$1$$ است و می‌توانیم از دو سمت معادله جذر بگیریم و جواب‌ها را به‌دست آوریم:

$$\large \begin {aligned} x ^ 2 & = 1 6 \\ { \sqrt { { x ^ 2 } } } & = { \sqrt { { 16 } } } \\ x & = \pm 4 \end {aligned}$$

حل معادله درجه 2 با فاکتورگیری

در حالتی که معادله درجه دوم به‌صورت حاصل‌ضرب دو معادله درجه اول باشد، یعنی $$(ax+b)(cx+d) = 0$$، که در آن $$ax+b$$ و $$xc+d$$ چندجمله‌ای درجه اول هستند، آنگاه جواب $$ax+b = 0$$ یا $$cx+d = 0$$ خواهد بود.

برای حل چنین معادلاتی، دو گام زیر را طی می‌کنیم:

1. هر عامل را برابر با $$0$$ قرار می‌دهیم.
2. معادله‌های گام قبل را حل می‌کنیم. جواب‌های این دو معادله خطی، جواب‌های معادله مرتبه دوم نیز هستند.

مثال ۲: جواب‌های معادله $$( x - 4 ) ( 3 x + 1 ) = 0$$ را به‌دست آورید.

حل: جواب‌ها به‌صورت زیر به‌دست می‌آیند:

$$\large \begin {aligned} { ( x - 4 ) } { ( 3 x + 1 ) } & = 0 \\ { x - 4 } & = 0 \\ x - 4 { + 4 } & = 0 { + 4 } \\ x & = 4 & { } \\ { 3 x + 1 } & = 0 \\ 3 x + 1 { - 1 } & = 0 { - 1 } \\ 3 x & = - 1 \\ \dfrac { 3 x } { { 3 } } & = \dfrac { - 1 } { { 3 } } \\ x & = -\dfrac { 1 } { 3 } & { } \end {aligned}$$

بنابراین، $$4$$ و $$- \frac 13$$ جواب‌های معادله هستند.

اگر بتوان یک معادله درجه 2 را به‌صورت حاصل‌ضرب دو عبارت خطی نوشت و به‌عبارتی از آن فاکتور گرفت، آنگاه می‌توان از صفر قرار دادن این عبارات برای به‌دست آوردن جواب استفاده کرد.

سمت چپ معادله را می‌توان به‌صورت ضرب عوامل $$(x+a)(x+b)$$ نوشت. در صورتی که

• $$a + b$$ برابر با ضریب جمله $$x$$ باشد.
• $$a b$$ برابر با جمله ثابت باشد.

مثال ۳: جواب‌های معادله $$x ^ 2 + 4 x - 5 = 0$$ را محاسبه کنید.

حل: باید موارد زیر را پیدا کنیم:

• $$a + b$$ برابر است با ضریب $$x$$، یعنی $$4$$.
• $$a b$$ برابر است با جمله ثابت، یعنی $$- 5$$.

با توجه به دو گزاره بالا، $$a = 5$$ و $$b = -1$$ به‌دست می‌آید.

$$\large \begin {aligned} x ^ 2 + 4 x - 5 & = 0 \\ { ( x + 5 ) } { ( x - 1 ) } & = 0 \\ { x + 5 } & = 0 \\ x + 5 { - 5 } & = 0 { - 5 } \\ x & = - 5 & { } \\ { x - 1 } & = 0 \\ x - 1 { + 1 } & = 0 { + 1 } \\ x & = 1 & { } \end {aligned}$$

بنابراین، جواب‌های معادله $$-5$$ و $$1$$ هستند.

اما اگر معادله دارای $$x$$ باشد یا به‌‌صورت ضرب دو چندجمله ای درجه اول نباشد یا نتوان از آن فاکتور گرفت، چگونه می‌توان ریشه را به‌دست آورد یا درباره وجود یا عدم وجود آن نظر داد. پاسخ این پرسش در فرمول دلتا است که در ادامه آن را معرفی می‌کنیم.

فرمول دلتا برای حل معادله درجه 2

روش دلتا، که البته نام صحیح آن فرمول درجه دوم است، با نام فرمول «شریدهارا آچاریا» (Shreedhara Acharya)، دانشمند زمان‌های دور یونان که آن را به‌دست آورد، نیز شناخته می‌شود. این روش بیان می‌کند که اکر یک چندجمله‌ای به‌فرم $$a x ^ 2 + b x + c$$ داشته باشیم، آنگاه می‌توانیم از فرمول $$x = \frac { - b \pm \sqrt { b ^ 2 - 4 a c } } { 2 a }$$ برای یافتن جواب آن، وقتی برابر با صفر قرار داده می‌شود، استفاده کنیم.

مثال ۴: فرض کنید تابع چندجمله‌ای $$f ( x ) = 3 x ^ 2 + 2 x - 3$$ را داریم. به‌ازای چه مقادیری از $$x$$ اندازه این تابع برابر با صفر خواهد شد؟

حل: با توجه به فرمولی که گفتیم، $$a = 3$$، $$b = - 2$$ و $$c = - 3$$ است. با استفاده از فرمول دلتا برای حل معادله درجه دوم، مقدار $$x$$ به‌صورت زیر به‌دست می‌آید:

$$\large x = \frac { -2 \pm \sqrt { 4 - 4 ( 3 ) ( - 3 ) } } { 2 ( 3 ) } = \frac { -2 \pm \sqrt { 40 } } { 6 } = \frac { - 1 } { 3 } \pm \frac { \sqrt { 1 0 } } { 3 } .$$

کاربرد روش دلتا در فاکتورگیری

از فرمول دلتا همچنین می‌توان برای فاکتورگیری استفاده کرد، به‌ویژه در مواردی که ریشه‌های یک چند‌جمله‌ای گویا نیستند.

مثال ۵: چندجمله‌ای $$x ^ 2 + x - 1 = 0$$ را به‌صورت حاصل‌ضرب دو عامل بنویسید.

حل: با استفاده از فرمولی که بیان کردیم، خواهیم داشت:

$$\large \phi = \frac { - b + \sqrt { b ^ 2 - 4 a c } } { 2 a } = \frac { - 1 + \sqrt { 5 } } { 2 } , \Phi = \frac { - b - \sqrt { b ^2 - 4 a c } } { 2 a } = \frac { - 1 - \sqrt { 5 }} { 2 } .$$

معادله درجه دوم به‌صورت زیر است:

$$\large k ( x - \phi ) ( x - \Phi ) = 0$$

اگر برای سادگی، $$k$$ را برابر با 12 درنظر بگیریم، خواهیم داشت:

$$\large ( x - \phi ) ( x - \Phi ) = \left ( x - \frac { - 1 + \sqrt { 5 } } { 2 } \right ) \left ( x - \frac { - 1 - \sqrt { 5 } } { 2 } \right ) .$$

تعیین ماهیت ریشه‌های معادله با فرمول دلتا

ماهیت ریشه‌های یک معادله درجه دوم را می‌توان با مشاهده دقیق فرمول دلتا تعیین کرد. فرمول دلتا از یک مبین تشکیل شده است که در واقع تفاوت را در فرمول ایجاد می‌کند و ما دو ریشه مختلف را نتیجه می‌دهد.

فرمول ریشه‌های معادله درجه دوم را می‌دانیم:

$$\large x = \frac { - b \pm \sqrt { b ^ 2 - 4 a c } } { 2 a }$$

برای هر معادله درجه دوم که به شکل استاندارد $$a x ^ 2 + b x + c = 0$$ نوشته شده است، مبین $$\Delta$$ به‌صورت زیر تعریف می‌شود (معمولاً چنین جا افتاده که به همین مبین فرمول دلتا گفته می‌شود):

$$\large \begin {cases} b ^ 2 - 4 a c \gt 0 : & \text{ (*) } \\ b ^ 2 - 4 a c = 0 : & \text{ (**) } \\ b ^ 2 - 4 a c \lt 0 : & \text { (***) } . \end {cases}$$

این سه‌ حالت به‌شرح زیر است:

• (*): دو ریشه مجزا و حقیقی
• (**): دو ریشه یکسان
• (***): دو ریشه مختلط

مثال ۶: نوع ریشه‌های دو معادله درجه دوم زیر را تعیین کنید:

$$\large \begin {aligned} 2 x ^ 2 + x - 1 & = 0 \\ x ^ 2 - 4 x + 4 & = 0 . \end {aligned}$$

حل: برای معادله درجه دوم $$2 x ^ 2 + x - 1 = 0$$، از آنجا که $$a = 2$$، $$b = 1$$ و $$x = - 1$$، داریم:

$$\large \begin {aligned} b ^ 2 - 4 a c & = 1 ^ 2 - 4 \times 2 \times - 1 \\ & = 9 >0 , \end {aligned}$$

که دلالت بر حقیقی و متمایز بودن ریشه‌ها دارد.

برای معادله درجه دوم $$x ^ 2 - 4x +4 = 0$$، از آنجا که $$a = 1$$، $$b = - 4$$ و $$c = 4$$:

$$\large \begin {aligned} b ^ 2 - 4 a c & = ( -4 ) ^ 2 - 4 \times 1 \times 4 \\ & = 0 , \end {aligned}$$

که نشان می‌دهد ریشه‌ها حقیقی و تکراری‌اند.

مثال ۷: مقدار $$k$$ را به‌‌گونه‌ای بیابید که چندجمله‌ای درجه دوم زیر ریشه‌های تکراری داشته باشد:

$$\large x ^ 2 + 4 x + k$$

حل: می‌دانیم که اگر $$\Delta = 0$$ باشد، آنگاه چندجمله‌ای درجه دوم ریشه‌های تکراری خواهد داشت. بنابراین، داریم:

$$\large \begin {aligned} b ^ 2 - 4 a c & = 0 \\ ( 4 ) ^ 2 - 4 ( 1 ) ( k ) & = 0 \\ k & = 4 . \end {aligned}$$

مثال ۸: نشان دهید معادله $$x ^ 2 + d x - 1 = 0$$ به‌ازای همه مقادیر $$d$$ دو ریشه حقیقی و متمایز دارد.

حل: در اینجا، $$a = 1$$، $$b = d$$ و $$c = - 1$$ است. بنابراین، فرمول مبین یا فرمول دلتا به‌صورت زیر است:

$$\Delta = d ^ 2 - 4 × 1 × - 1 = d ^ 2 + 4 .$$

از آنجا که $$d ^ 2$$ یک مربع کامل است، اندازه آن همیشه بزرگ‌تر از $$0$$ است. بنابراین، داریم:

$$\large \Delta = d ^ 2 + 4 \geq 4 .$$

در نتیجه، مبین همیشه بزرگ‌تر از $$0$$ است و این یعنی اینکه این معادله دارای ریشه‌های حقیقی برای هر مقدار حقیقی $$d$$ است.

اثبات فرمول دلتا

فرمول دلتا را می‌توان با روش‌های مختلفی اثبات کرد. در ادامه این روش‌ها را بیان می‌کنیم.

روش اول اثبات فرمول دلتا

از $$a x ^ 2 + b x + c = 0$$ شروع می‌کنیم. $$c$$ را از هر دو طرف معادله کم می‌کنیم و خواهیم داشت: $$a x ^ 2 + bx = - c$$. اکنون هر دو طرف معادله را بر $$a$$ تقسیم می‌کنیم و به تساوی $${ x } ^ { 2 } + \frac { b x } { a } = \frac { - c } { a }$$ می‌رسیم. جمله $$\dfrac { { b } ^ { 2 } } { 4 { a } ^ { 2 } }$$ را به دو طرف معادله اضافه می‌کنیم و خواهیم داشت:

$$\large { x } ^ { 2 } + \frac { b x } { a } + \frac { { b } ^ { 2 } } { 4 { a } ^ { 2 } } =\frac { - c } { a } + \frac { { b } ^ { 2 } } { 4 { a } ^ { 2 } } .$$

سپس می‌توانیم مربع سمت چپ را کامل کنیم تا داشته باشیم:

$$\large \left ( x + \frac { b } { 2 a } \right ) ^ 2 = \frac { - c }{ a } + \frac { { b } ^ { 2 } } { 4 { a } ^ { 2 } }$$

سمت راست معادله را ساده می‌کنیم و داریم:

$$\large \displaystyle \left ( x + \frac { b } { 2 a } \right ) ^ { 2 } = \frac { { b } ^ { 2 } - 4 a c } { 4 { a } ^ { 2 } } .$$

اکنون، ریشه مربع دو سمت معادله را می‌گیریم:

$$\large x + \frac { b } { 2 a } = \frac { \pm \sqrt { { b } ^ { 2 } - 4 a c } } { 2 a } .$$

سپس، $$\dfrac { b }{ 2a }$$ را از دو طرف تساوی کم می‌کنیم و اثبات کامل می‌شود:

$$\large x = \dfrac { - b \pm \sqrt { b ^ 2 - 4 a c } } { 2 a } .$$

روش دوم اثبات فرمول دلتا

از $$a x ^ 2 + b x + c = 0$$ شروع می‌کنیم. دو طرف این معادله را در $$4a$$ ضرب می‌کنیم و خواهیم داشت: $$4 a ^ { 2 } x ^ { 2 } + 4 a b x + 4 ac=0$$. توجه کنید که $$4 a ^ { 2 } x ^ { 2 } + 4 ab x$$ مربع $$2 a x + b$$ است، یا به‌طور دقیق‌تر، $$( 2 a x + b ) ^ { 2 } - b ^ { 2 }$$.

اکنون معادله به‌صورت زیر درمی‌آید:

$$\large \begin {aligned} ( 2 a x + b ) ^ { 2 } - b ^ { 2 } + 4 a c & = 0 \\ ( 2 a x + b ) ^ { 2 } & = b ^ { 2 } - 4 a c \\ \sqrt { ( 2 a x + b) ^ { 2 } } & =\pm \sqrt { b ^ { 2 } - 4 a c } \\ 2 a x + b & = \pm \sqrt { b ^ { 2 } - 4 a c } \\ 2 a x & = - b \pm \sqrt { b ^ { 2 } - 4 a c } \\ x & = \dfrac { - b \pm \sqrt { b ^ { 2 } - 4 a c } } { 2 a } . \end{aligned}$$

روش سوم اثبات فرمول دلتا

عبارت $$x = y - \dfrac { b } { 2 a }$$ را در معادله جایگذاری می‌کنیم:

$$\large \begin {aligned} a \left ( y - \dfrac { b }{ 2 a } \right ) ^ 2 + b \left ( y - \dfrac { b } { 2 a } \right ) + c & = 0 \\ a y ^ 2 -b y + \dfrac { b ^ 2 } { 4 a } + b y - \dfrac { b ^ 2 } { 2 a } + c & = 0 . \end{aligned}$$

از این رابطه، به‌راحتی می‌توان $$y$$ را به‌دست آورد:

$$\large \begin {aligned} a y ^ 2 - \dfrac { b ^ 2} { 4 a } + c & = 0 \\ y ^ 2 & = \dfrac {b ^ 2 - 4 a c } { 4 a ^ 2 } \\ y & = \pm \dfrac { \sqrt { b ^ 2 - 4 a c } } { 2 a } . \end {aligned}$$

در نهایت، تغییر متغیر را برمی‌گردانیم:

$$\large x = \dfrac { - b \pm \sqrt { b ^ 2 - 4 a c } } { 2 a } .$$

روش چهارم اثبات فرمول دلتا

این روش اثبات بر اساس «فرمول ویت» (Vieta's Formula) است. فرض کنید $$x_1$$ و $$x _ 2$$ ریشه‌های معادله $$a x ^ 2 + bx + c = 0$$ باشند. بر اساس فرمول ویت، داریم:

$$\large \begin {aligned} x _ 1 + x _ 2 & = - \dfrac { b } { a } \\ x _ 1 x _ 2 & = \dfrac { c } { a } . \end {aligned}$$

دو طرف معادله اول را به توان دو می‌رسانیم و معادله دوم را در 4 ضرب می‌کنیم:

$$\large \begin {aligned} x _ 1 ^ 2 + 2 x _ 1 x _ 2 + x _ 2 ^ 2 = \dfrac { b ^ 2 } { a ^ 2 } \\ 4 x _ 1 x _ 2 = \dfrac { 4 c }{ a } . \end {aligned}$$

سپس، دو معادله را از هم کم می‌کنیم:

$$\large x _ 1 ^ 2 - 2 x _ 1 x _ 2 + x _ 2 ^ 2 = \dfrac { b^ 2 - 4 a c } { a^ 2 } .$$

سمت چپ مربع کامل است:

$$\large ( x _ 1 - x _ 2 ) ^ 2 = \dfrac { b ^ 2 - 4 a c } { a ^ 2 } \implies x _ 1 - x _ 2 = \dfrac { \sqrt { b ^ 2 - 4 a c } } { a } .$$

در نهایت، با استفاده از مجموع و تفاضل ریشه‌ها استفاده می‌کنیم و ریشه‌ها را به‌دست می‌آوریم:

$$\large \begin {aligned} x _ 1 & = \dfrac { - b + \sqrt { b ^2 - 4 a c } } { 2 a } \\\\ x _ 2 & = \dfrac { - b - \sqrt { b ^ 2 - 4 a c } } { 2 a } . \end {aligned}$$

مثال‌های فرمول دلتا

در این بخش‌، چند مثال را از روش حل معادله درجه ۲ با روش دلتا را بررسی می‌کنیم.

مثال اول فرمول دلتا

معادله $$x ^ 2 - 2 0 x - 6 9 = 0$$ را حل کنید.

حل: مقادیر $$a = 1$$، $$b = - 20$$ و $$c = - 69$$ را در فرمول دلتا جایگذری می‌کنیم و خواهیم داشت:

$$\large \begin {aligned} x & = \dfrac { - ( - 2 0 ) \pm \sqrt { ( - 2 0 ) ^ 2 - 4 × 1 × - 6 9 } } { 2 × 1 } \\ & = \dfrac { 2 0 \pm \sqrt { 4 0 0 + 2 7 6 } } { 2 } \\ & = \dfrac { 2 0 \pm \sqrt { 6 7 6 } } { 2 } \\ & = \dfrac { 2 0 \pm 2 6 } { 2 } \\ \Rightarrow x & = 23 \, \text{ or }\, x = - 3 . \end {aligned}$$

مثال دوم فرمول دلتا

معادله $$x ^ 2 - 6 x = 9$$ را حل کنید.

حل: باید آن را به‌‌صورت $$a x ^ 2 + b x + c = 0$$ بنویسیم:

$$\large \begin {aligned} x ^ 2 - 6 x & = 9 \\ x ^ 2 - 6 x { - 9 } & = 9 { - 9 } \\ x ^ 2 - 6 x - 9 & = 0 \end {aligned}$$

اکنون می‌توانیم مقادیر را در فرمول قرار داده و برای $$a = 1$$، $$b = - 6$$ و $$c = - 9$$، نوشت:

$$\large \begin {aligned} x & = \dfrac {- { b } \pm \sqrt { { b } ^ 2 - 4 { a } { c } } } { 2 } \\ & = \dfrac { -( { - 6 } ) \pm \sqrt { ( { - 6 } ) ^ 2 - 4 ( { 1 } ) ( { - 9 } )} } { 2 ( { 1 } ) } \\ & = \dfrac { 6 \pm \sqrt { 3 6 - ( - 36 ) } } { 2 } \\ & = \dfrac { 6 \pm \sqrt { 7 2 } } { 2 } \\ & = \dfrac { 6 \pm \sqrt { 3 6 \cdot 2 } } { 2 } \\ & = \dfrac { 6 \pm \sqrt { 3 6 } \cdot \sqrt { 2 } } { 2 } \\ & = \dfrac { 6 \pm 6 \sqrt { 2 } } { 2 } \\ & = 3 \pm 3 \sqrt { 2 } \end {aligned}$$

مثال سوم فرمول دلتا

معادله $$x ^ { 4 } - 3 x ^ { 2 } + 1 = 0$$ را حل کنید.

حل: همان‌طور که می‌بینیم، این معادله درجه 4 است، اما با در نظر گرفتن تغییر متغیر $$u = x ^ 2$$‌ آن را به یک معادله درجه دوم تبدیل می‌کنیم:

$$\large u ^ { 2 } - 3 u + 1 = 0 .$$

اکنون می‌توانیم از فرمول دلتا استفاده کنیم:

$$\large u = \dfrac { 3 \pm \sqrt { 5 } } { 2 } .$$

اکنون $$u$$ را به‌دست آورده‌ایم. اما هدف به‌دست آوردن $$x$$ است. از آنجا که $$u = x ^ { 2 } = \frac { 3 \pm \sqrt { 5 } } { 2 }$$، جواب برای $$x$$ به‌صورت زیر خواهد بود:

$$\large x = \pm \sqrt { \dfrac { 3 \pm \sqrt { 5 } } { 2 } } .$$

مثال چهارم فرمول دلتا

معادله درجه 2 زیر را حل کنید.

$$\large 2{z^2} + z - 72 = {z^2} - 2z + 58$$

حل: ابتدا باید معادله را به‌فرم استاندارد بنویسیم:

$$\large {z^2} + 3z - 130 = 0$$

در معادله بالا، همه جملات را به سمت چپ انتقال داده‌ایم.

اکنون باید مقادیر $$a$$، $$b$$ و $$c$$ فرمول دلتا را تعیین کنیم:

$$\large a = 1\hspace{0.25in}b = 3\hspace{0.25in}c = - 130$$

با قرار دادن این مقادیر در فرمول دلتا، خواهیم داشت:

$$\large z = \frac { { - 3 \pm \sqrt { { { \left ( 3 \right ) } ^ 2 } - 4 \left ( 1 \right ) \left ( { - 130 } \right ) } } } { { 2 \left ( 1 \right ) } } = \frac { { - 3 \pm \sqrt {529} } } { 2 } = \frac { { - 3 \pm 2 3 } } { 2 }$$

بنابراین، دو ریشه به‌صورت زیر خواهند بود:

$$\large z = \frac { { - 3 - 23 } } { 2 } = - 13,\,\,\,\,\,z = \frac { { - 3 + 23 } } { 2 } = 10$$

مثال پنجم فرمول دلتا

معادله زیر را حل کنید:

$$\large 9{w^2} - 6w = 101$$

حل: ابتدا باید مقادیر مربوط به فرمول دلتا را تعیین کنیم:

$$\large a = 9\hspace{0.25in}b = - 6\hspace{0.25in}c = - 101$$

با قرار دادن این مقادیر در فرمول، خواهیم داشت:

$$\large \begin {align*} w & = \frac { { - \left ( { - 6 } \right ) \pm \sqrt { { { \left ( { - 6 } \right ) } ^ 2 } - 4 \left ( 9 \right ) \left ( { - 101 } \right ) } } } { { 2 \left ( 9 \right ) } } \\ & = \frac { { 6 \pm \sqrt { 3672} }}{ { 1 8 } } = \frac { { 6 \pm \sqrt { \left ( { 3 6 } \right ) \left ( {102} \right ) } } } { { 1 8 } } \\ & = \frac { { 6 \pm 6 \sqrt {102} }} { { 1 8 } } = \frac { { 1 \pm \sqrt { 102} }} { 3 } \end {align*}$$

بنابراین، دو جواب به‌صورت زیر خواهند بود:

$$ \large { {w = \frac { 1 } { 3 } - \frac { { \sqrt {102} }} { 3 } \, \, {\mbox{, }} \, \, w = \frac { 1 } { 3 } + \frac { { \sqrt {102} }} { 3 } } } $$