زاویه قائمه چیست؟ – به زبان ساده + حل مثال های تصویری

زاویه قائمه زاویه‌ای برابر با ۹۰ درجه است. به محیط اطراف خود نگاه کنید. گوشه‌های اتاق، میز، جعبه‌ها، صفحه نمایش تلفن همراه و بسیاری از وسیله‌ها و اجسامی که روزانه با آن‌ها سر و کار دارید، از شکل‌هایی با زاویه راست (قائمه) تشکیل می‌شوند. در این مقاله، به ارائه تعریف‌ها، کاربردها، روش‌های اندازه‌گیری و روش‌های رسم زاویه قائمه به همراه حل چندین مثال می‌پردازیم.

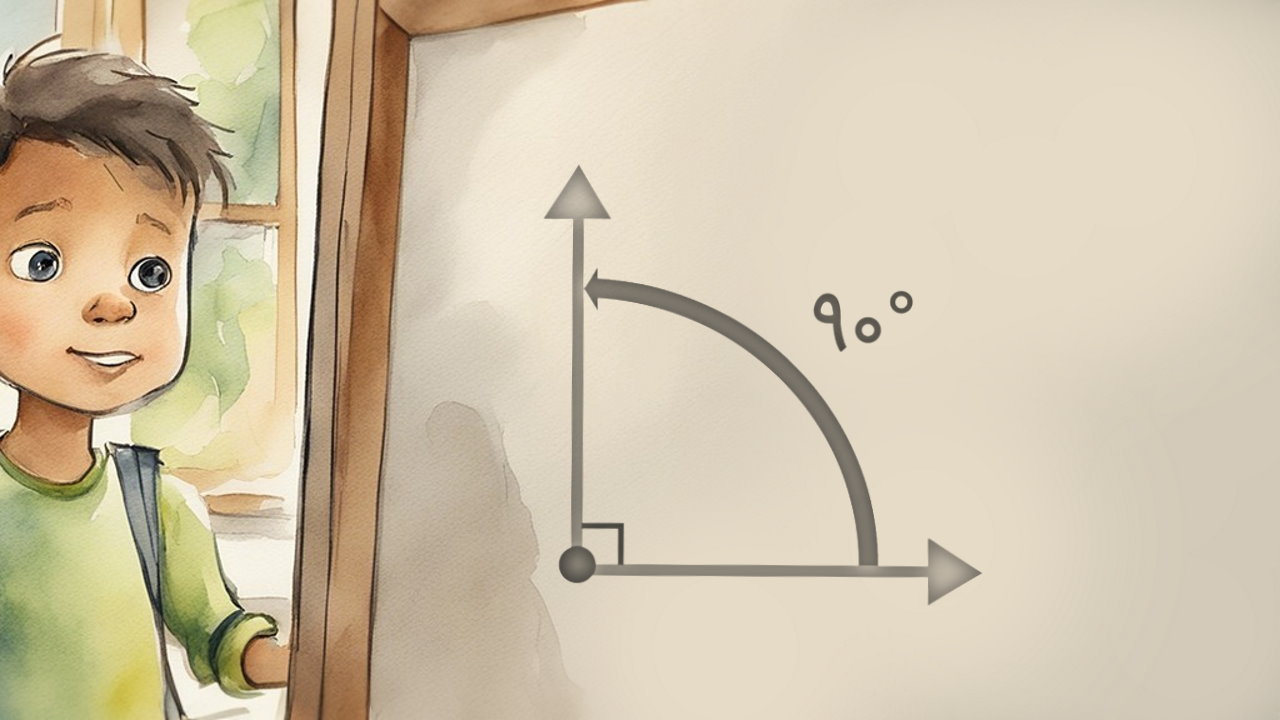
زاویه و انواع آن چیست؟

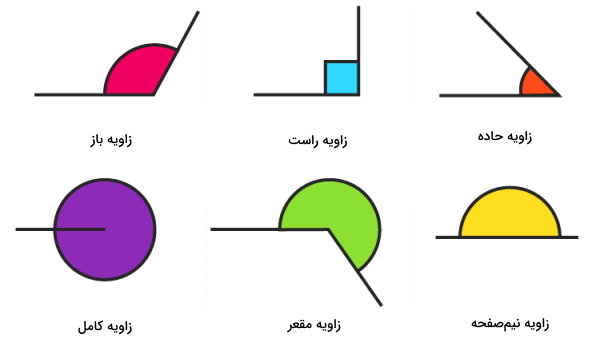
زاویه، شکلی است که از برخورد دو نیم‌خط به وجود می‌آید. اگر نقطه شروع دو نیم‌خط، مشترک باشد، یک زاویه تشکیل می‌شود. زاویه‌ها را می‌توان بر اساس میزان بازشدگی بین دو نیم‌خط (اندازه زاویه)، به انواع صفر، تند، راست، باز، نیم‌صفحه، کاو و تمام‌صفحه تقسیم کرد.

زاویه راست چیست ؟

زاویه قائمه یا «زاویه راست» (Right Angle)، زاویه‌ای با اندازه ۹۰ درجه است. هنگامی که دو نیم‌خط، یکدیگر را با زاویه ۹۰ درجه قطع می‌کنند یا اصطلاحا بر هم عمود می‌شوند، می‌گویند این دو نیم‌خط با یکدیگر زاویه راست یا قائمه می‌سازند.

تصویر زیر به شما نشان می‌دهد که زاویه قائمه چه شکلی است.

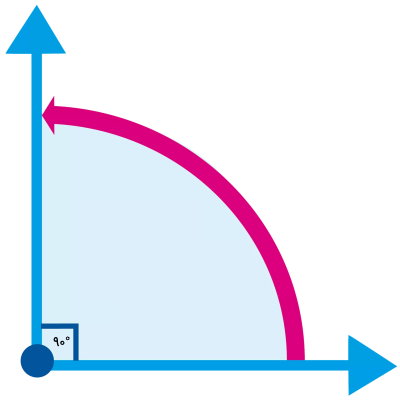
علامت زاویه راست یا قائمه چیست ؟

زاویه قائمه نیز مانند دیگر انواع زاویه ها، از یک راس و دو ضلع تشکیل می‌شود. نکته متفاوت در نمایش زاویه‌های راست، استفاده از علامت □ در گوشه یا راس آن‌ها است. به عنوان مثال، وجود علامت □ بر روی گوشه زاویه «م ر ح» در تصویر زیر، قائمه بودن آن را نشان می‌دهد.

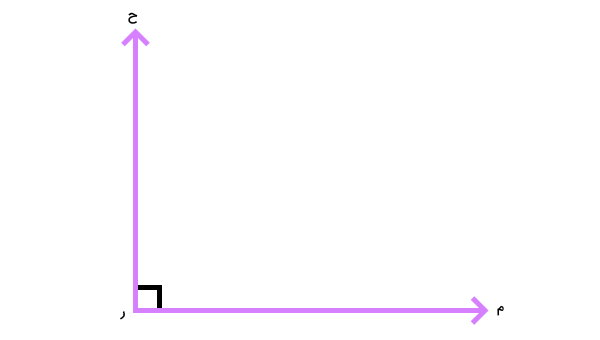
علاوه بر علامت □ در شکل زاویه راست، هنگام نوشتن این نوع زاویه در روابط هندسی، از علامت ∟ استفاده می‌شود. عبارت زیر را در نظر بگیرید:

ABC∟

این عبارت، به معنای راست بودن زاویه ABC است.

زاویه قائمه بر حسب رادیان

زاویه‌ها معمولا با واحد «درجه» بیان می‌شوند. به عنوان مثال، زاویه بین ضلع‌های مربع برابر با ۹۰ درجه است. «رادیان»، یکی دیگر از واحدهای متداول برای بیان زاویه‌ها به شمار می‌رود. این واحد، زاویه را به صورت کسری از عدد پی (π) نمایش می‌دهد. زاویه قائمه بر حسب رادیان برابر است با:

$$\frac { \pi } { ۲ }$$

عبارت بالا به صورت پی دوم خوانده می‌شود.

نمونه زاویه راست در دنیای واقعی

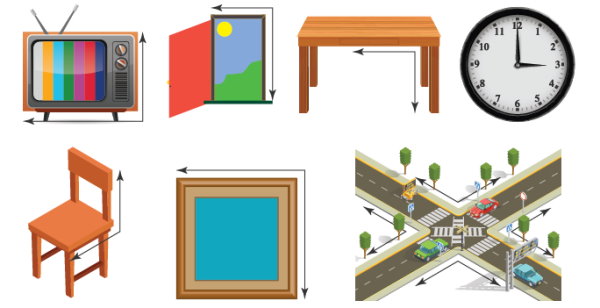
زاویه راست، رایج‌ترین زاویه است که می‌توانید آن را تقریبا در هر محلی مشاهده کنید. گوشه‌های در، تلویزیون، چهارراه، کتاب و بسیاری اجسام دیگر دارای زاویه قائمه هستند. تصویر زیر، برخی چند نمونه زاویه راست در دنیای واقعی را نمایش می‌دهد.

مثال ۱: تعیین زاویه قائمه روی ساعت

عقربه‌های ساعت، با یکدیگر زاویه‌های مختلفی می‌سازند. در کدامیک از زمان‌های زیر، زاویه بین عقربه ساعت و عقربه دقیقه برابر با ۹۰ درجه است؟

در تصویر بالا، فقط عقربه‌های ساعت سبز رنگ با یکدیگر زاویه ۹۰ درجه می‌سازند. نوع زوایای دیگر به ترتیب عبارت است از:

• ساعت نارنجی: تند
• ساعت قرمز: باز
• ساعت بنفش: نیم‌صفحه
• ساعت آبی: باز

مثال ۲: محاسبه زاویه به کمک زاویه قائمه

دو زاویه «الف» و «ب»، با یکدیگر یک زاویه راست می‌سازند. اگر اندازه زاویه «ب» برابر با ۳۰ درجه باشد، اندازه زاویه «الف» چقدر است؟

اندازه زاویه‌های راست برابر با ۹۰ درجه است. بنابراین داریم:

۹۰° = زاویه «ب» + زاویه «الف»

اندازه زاویه «ب» را در رابطه بالا قرار می‌دهیم:

۹۰° = ۳۰° + زاویه «الف»

۳۰° - ۹۰° = زاویه «الف»

۶۰° = زاویه «الف»

مطالب مرتبط با این مبحث:

• انواع زاویه چیست؟
• زاویه مکمل چیست؟
• زاویه متمم چیست؟
• زاویه متقابل به راس چیست؟
• زاویه محاطی چیست؟

اندازه گیری زاویه راست چگونه انجام می‌شود ؟

بهترین وسایل مورد استفاده برای اندازه گیری و تشخیص زاویه قائمه، گونیا و نقاله هستند. در ادامه، نحوه به کارگیری این ابزارهای هندسی را به صورت تصویری توضیح می‌دهیم.

گونیا: ابزار تشخیص قائمه بودن یا نبودن زاویه

گونیا، وسیله‌ای به شکل مثلث قائم الزاویه است. مانند این مثلث، گونیا نیز یک گوشه با زاویه ۹۰ درجه دارد. راس قائمه گونیا، برای تعیین راست بودن زاویه‌ها یا رسم زاویه‌های راست مورد استفاده قرار می‌گیرد.

کتاب یا دفتر خود را بر دارید. اغلب کتاب‌ها و دفترها، مستطیلی شکل هستند. مستطیل، از چهار راس با زاویه ۹۰ درجه تشکیل می‌شود.

در اینجا قصد داریم قائمه بودن زاویه گوشه‌های کتاب را بررسی کنیم. به این منظور، گونیای خود را بر روی کتاب قرار می‌دهیم.

سپس، گونیا را به گونه‌ای جابجا می‌کنیم که گوشه راست آن بر روی گوشه کتاب قرار بگیرید.

بدون تغییر دادن موقعیت گوشه‌ها، گونیا را می‌چرخانیم تا یکی از ساق‌های آن بر روی یکی از ضلع‌های کتاب منطبق شود.

منطبق شدن هر دو ساق گونیا بر روی هر دو ضلع کتاب (مانند تصویر بالا)، نشان دهنده راست بودن زاویه گوشه است. بررسی زاویه‌ها را برای تمام گوشه‌های کتاب تکرار کنید. با این کار، مشاهده خواهید کرد که مستطیل، ۴ زاویه راست دارد.

مثال ۳: تعیین زاویه های قائمه متوازی الاضلاع

تصویر زیر، شکل یک متوازی الاضلاع را نمایش می‌دهد. تعداد زاویه‌های قائمه این شکل را تعیین کنید.

به منظور تعیین تعداد زاویه‌های راست متوازی الاضلاع بالا، مطابق با روش توضیح داده شده در بخش قبل، گونیا را بر روی تمام گوشه‌های شکل تنظیم می‌کنیم.

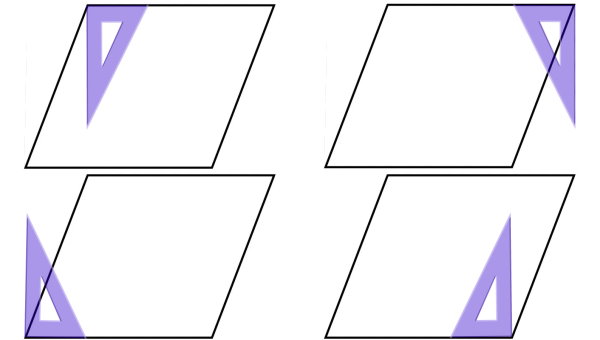
بر اساس تصویر بالا، در تمام گوشه‌ها، ضلع متوازی الاضلاع، ساق گونیا را قطع می‌کند. بنابراین، هیچ یک از گوشه‌های متوازی الاضلاع دارای زاویه ۹۰ درجه نیست.

مثال ۴: تعیین زاویه های قائمه ذوزنقه

در ذوزنقه زیر، چند زاویه راست وجود دارد؟ به این ذوزنقه چه می‌گویند؟

با استفاده از گونیا، نوع زاویه هر یک از راس‌های ذوزنقه را مشخص می‌کنیم.

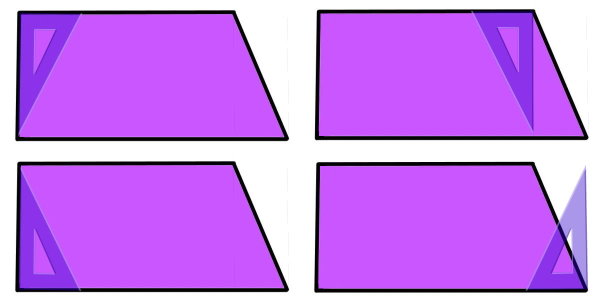
همان‌طور که مشاهده می‌کنید، ذوزنقه بالا، دو زاویه راست دارد. به این ذوزنقه، ذوزنقه قائم الزاویه می‌گویند.

نقاله: اندازه گیری دقیق زاویه راست

نقاله، وسیله دقیق‌تری برای اندازه‌گیری زاویه‌ها و تشخیص نوع آن‌ها است. روی کمان این ابزار نیم‌دایره‌ای شکل، اعداد و خطوط نشان‌دهنده زاویه‌های ۰ تا ۱۸۰ درجه، در دو جهت وجود دارند.

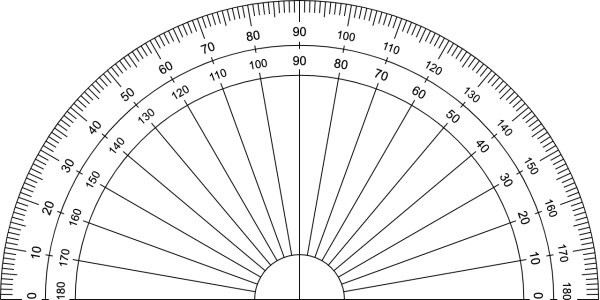
به منظور نمایش نحوه کار با نقاله، از سطح یک برگه کاغذ استفاده می‌کنیم. نقاله را بر روی کاغذ قرار دهید.

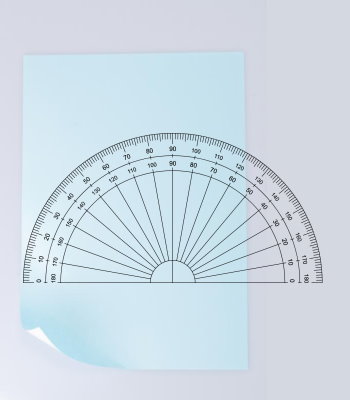
مرکز نقاله را با یکی از گوشه‌های کاغذ تنظیم کنید. نقاله را به گونه‌ای بچرخانید که خط مبنای آن بر رویی لبه کاغذ منطبق شود.

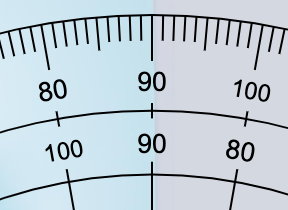
خط لبه دیگر کاغذ، از کنار یکی از اعداد روی نقاله عبور می‌کند. این عدد زاویه گوشه کاغذ را نمایش می‌دهد. اگر عدد کنار خط لبه کاغذ برابر با ۹۰ باشد (مانند تصویر زیر)، گوشه مورد بررسی، دارای زاویه راست است.

رسم زاویه راست چگونه است ؟

به منظور راسم زاویه راست، می‌توان از گونیا و نقاله استفاده کرد. گونیا، ابزار سریع‌تری برای انجام این کار است. در ادامه، رسم زاویه قائمه با هر دوی این وسایل را توضیح می‌دهیم.

رسم زاویه قائمه با گونیا

ساده‌ترین و سریع‌ترین روش برای رسم یک زاویه قائمه، استفاده از گونیا است. گونیا بر روی یک صفحه قرار دهید. موقعیت قرارگیری گونیا، اهمیت زیادی ندارد. فقط توجه داشته باشید که در حین رسم، گونیا جابجا نشود.

قلم خود را بر روی یکی از گوشه‌های گونیا قرار دهید. سپس، یک خط در کنار ساق گونیا بکشید.

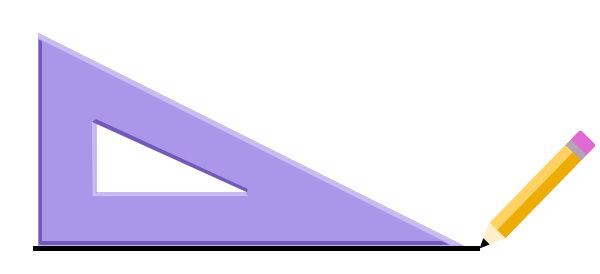
همین کار را در کنار ساق دیگر تکرار کنید.

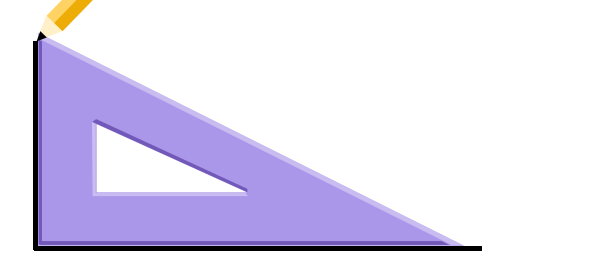
گونیا را بردارید. شکل به دست آمده، یک زاویه راست است.

رسم زاویه قائمه با نقاله

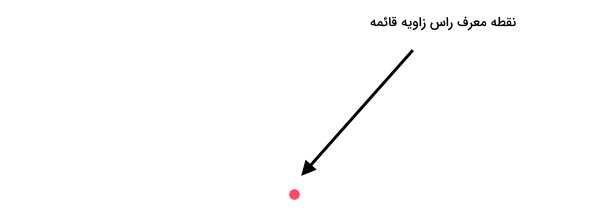
برای رسم زاویه راست با نقاله، نقطه‌ای از صفحه را به عنوان راس زاویه در نظر بگیرید.

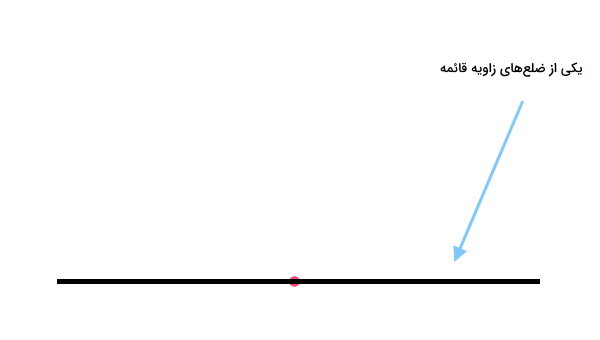
سپس، خطی را در جهت مورد نظر از روی نقطه عبور دهید. این خط، به عنوان یکی از ضلع‌های زاویه قائمه در نظر گرفته می‌شود.

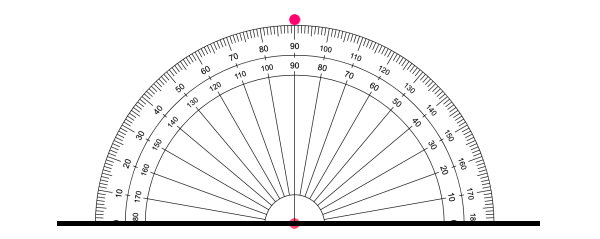
مرکز نقاله را با نقطه و خط مبنای آن را با خط رسم شده تطابق دهید. در کنار عدد ۹۰ درجه بر روی کمان نقاله، یک علامت بزنید.

نقاله را بردارید و یک خط بین راس زاویه و نقطه علامت زده شده در تصویر بالا رسم کنید.

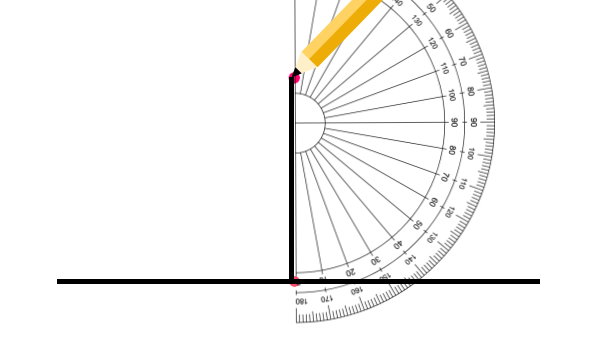
با انجام مراحل بالا، یک زاویه قائمه به دست می‌آید.

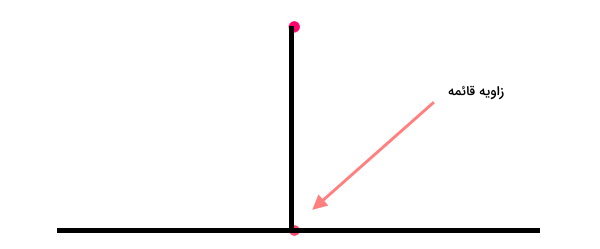
مثال ۵: رسم شکل با زاویه راست

یک چندضلعی با دو زاویه راست رسم کنید.

به منظور چندضلعی با دو زاویه راست، می‌توانیم از گونیا یا نقاله استفاده کنیم. توجه داشته باشید که بر اساس فرمول مجموع زوایای داخلی، تعداد ضلع‌های چندضلعی باید بیشتر از سه باشد. در مثال، یک پنج ضلعی با دو زاویه ۹۰ درجه را رسم می‌کنیم. برای شروع، یک نقطه را به عنوان یکی از راس‌های پنج‌ضلعی در نظر می‌گیریم.

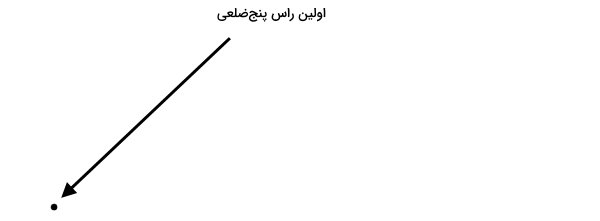
گوشه قائمه گونیا را بر روی نقطه قرار می‌دهیم و یک زاویه راست می‌‌کشیم.

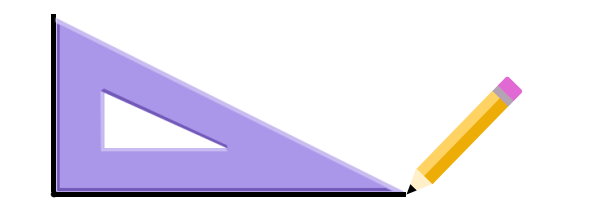
انتهای ضلع‌های زاویه را با نقطه مشخص می‌کنیم. این نقاط، دو راس دیگر پنج‌ضلعی خواهند بود.

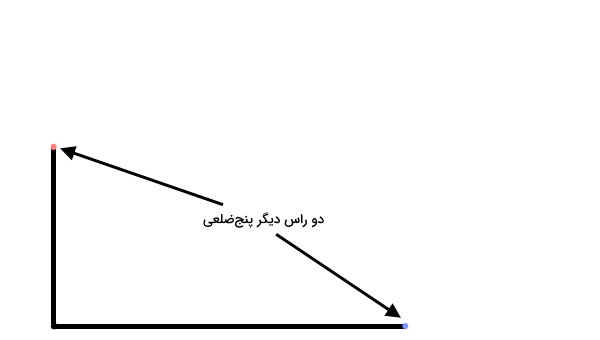
در ادامه، گوشه ۹۰ درجه‌ای گونیا را بر روی یکی از راس‌های دیگر قرار می‌دهیم و آن را به شکل زیر تنظیم می‌کنیم.

سپس، خطی را مشابه تصویر زیر، در کنار ساق دیگر گونیا رسم می‌کنیم.

نقطه انتهایی این خط را نیز به عنوان راس چهارم پنج‌ضلعی در نظر می‌گیرم.

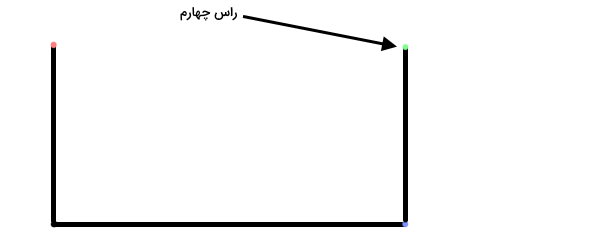
اکنون دو زاویه ۹۰ درجه، سه ضلع و چهار راس داریم. نقطه‌ای را به عنوان راس پنجم، در یک محل مناسب انتخاب می‌کنیم.

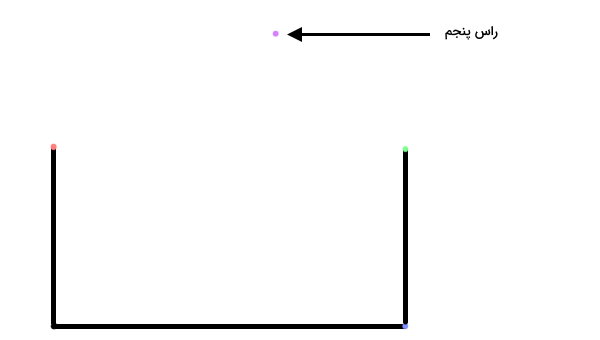
از نقطه بالا، دو پاره‌خط به راس‌های نزدیک وصل می‌کنیم.

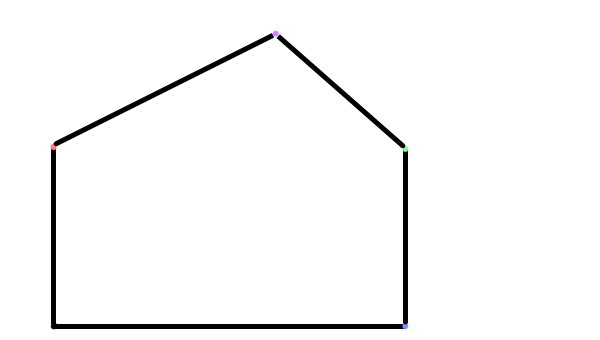
اکنون، یک پنج‌ضلعی با دو زاویه راست داریم. دو زاویه راست، همان‌هایی هستند که ضلع‌های آن‌ها را توسط گونیا رسم کردیم.

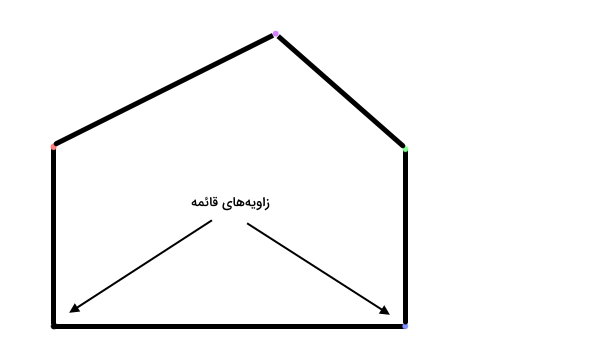
مثلث قائم الزاویه چیست ؟

مبحث زاویه راست، بدون اشاره به مثلث‌های قائم الزاویه، تکمیل نمی‌شود. مثلث قائم الزاویه، از یک زاویه ۹۰ درجه و دو زاویه کوچکتر از ۹۰ درجه (زاویه تند) تشکیل می‌شود.

ویژگی‌های این مثلث، آن را به یکی از پرکاربردترین شکل‌های هندسی تبدیل کرده است. علاوه بر این، نسبت‌های بین ضلع‌های مثلث قائم الزاویه، در نوشتن روابط مثلثاتی نیز مورد استفاده قرار می‌گیرند.

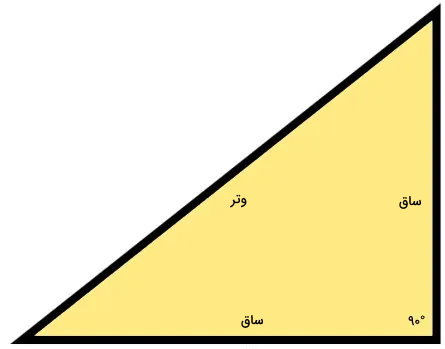
به ضلع‌های متصل به گوشه قائمه، ساق و به ضلع مقابل آن، وتر می‌گویند. رسم مثلث قائم الزاویه، معمولا با استفاده گونیا یا نقاله انجام می‌گیرد. به این منظور، کافی است مراحل رسم زاویه راست را طی کرده و سپس، دو ضلع زاویه را به یکدیگر وصل کنید. شکل به دست آمده، یک مثلث قائم الزاویه است.

سوالات متداول در رابطه با زاویه قائمه

در این بخش، به برخی از سوالات پرتکرار در رابطه با زاویه‌های راست به صورت خلاصه پاسخ می‌دهیم.

تعریف زاویه راست چیست ؟

زاویه راست، زاویه‌ای با اندازه ۹۰ درجه است،

نام دیگر زاویه قائمه چیست ؟

نام دیگر زاویه قائمه ، زاویه راست است.

زاویه راست چند درجه است ؟

۹۰ درجه.

مربع چند زاویه راست دارد ؟

هر مربع، چهار زاویه راست یا قائمه دارد.

مستطیل چند زاویه راست دارد ؟

مستطیل، چهار زاویه راست دارد.

مثلث چند زاویه راست دارد ؟

هر مثلث می‌تواند حداکثر یک زاویه قائمه داشته باشد.

لوزی چند زاویه راست دارد ؟

لوزی هیچ زاویه ۹۰ درجه‌ای ندارد.

لوزی با زاویه قائمه چه نام دارد ؟

اگر یک چهارضلعی با ویژگی‌های لوزی، زاویه قائمه داشته باشد، به آن چهارضلعی، مربع می‌گویند.

متوازی الاضلاع چند زاویه قائمه دارد ؟

متوازی الاضلاع هیچ زاویه ۹۰ درجه‌ای ندارد. البته مربع و مستطیل، حالت‌های خاص متوازی الاضلاع با زاویه راست هستند.

آیا شش ضلعی زاویه راست دارد ؟

یک شش‌ضلعی می‌تواند زاویه راست داشته باشد. با این وجود، شش‌ضلعی منتظم، هیچ زاویه قائمه‌ای ندارد.

دایره چند زاویه راست دارد ؟

دایره هیچ گوشه و زاویه ۹۰ درجه‌ای ندارد. اگر منظور، زاویه مرکزی دایره باشد، این شکل به چهار زاویه مرکزی ۹۰ درجه تقسیم می‌شود.

به زاویه ای که از زاویه راست کوچکتر باشد چه می‌گویند ؟

حاده یا تند.

به زاویه ای که از زاویه راست بزرگتر باشد چه می‌گویند ؟

منفرجه یا باز.

دو زاویه راست تشکیل چه زاویه ای می دهند؟

نیم‌صفحه. مجموع دو زاویه راست برابر با ۱۸۰ درجه یا همان زاویه نیم‌صفحه است.

زاویه قائمه چه کسری از زاویه نیم صفحه است ؟

یک‌دوم.

ثلث زاویه قائمه چقدر است ؟

ثلث زاویه راست برابر با ۳۰ درجه است.

نیمساز زاویه قائمه چیست ؟

نیمساز زاویه راست برابر با ۴۵ درجه است.

مکمل زاویه قائمه یک زاویه چیست ؟

مکمل زاویه راست یک زاویه راست است.