رگرسیون طبقه ای با مقیاس بهینه در SPSS — راهنمای کاربردی

تحلیل و روشهای رگرسیونی برای ایجاد مدلهای آماری در «یادگیری ماشین» (Machine Learning) به کار میروند. یکی از روشهای رگرسیونی که برای مدلسازی روی متغیرهای طبقهای مورد استفاده قرار میگیرد، Optimal Scaling یا روش رگرسیون طبقهای با مقیاس بهینه نام دارد که خوشبختانه در SPSS نیز به عنوان یک روش تحلیلی گنجانده شده است. در این نوشتار به رگرسیون طبقه ای با مقیاس بهینه در SPSS خواهیم پرداخت و به کمک یک مثال، نحوه اجرای آن را در این نرم افزار کاربردی فرا میگیریم.
برای آشنایی بیشتر با رگرسیون خطی برای متغیرهای طبقهای نوشتار رگرسیون خطی با متغیرهای طبقه ای در SPSS — راهنمای گام به گام را بخوانید. همچنین خواندن نوشتارهای رگرسیون چندگانه در SPSS — راهنمای کاربردی و رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده نیز خالی از فایده نیست.
رگرسیون طبقه ای با مقیاس بهینه در SPSS
قبل از هر چیز تفاوت بین مدل رگرسیون با متغیرهای پیشگو طبقهای و رگرسیون با متغیر پاسخ طبقهای را متذکر میشویم. در مدل رگرسیون با متغیرهای پیشگو طبقهای، از متغیرهای گسسته و اسمی یا ترتیبی برای پیشبینی مقدار متغیر وابسته استفاده میشود. فرض بر این است که متغیر وابسته از نوع عددی و دارای مقادیر پیوسته است. ولی در مدل رگرسیون با متغیر پاسخ طبقهای، قرار است براساس متغیرهای پیشگو، مدلی برای طبقهبندی کردن مشاهدات ایجاد کنیم. در حقیقت متغیر پاسخ، شماره گروه یا طبقه هر مشاهده را نشان میدهد.
در اینجا زمانی که از رگرسیون طبقهای با مقیاس بهینه صحبت میکنیم، نوع اول مدل رگرسیونی مد نظر است. به این معنی که قرار است به واسطه متغیرهای پیشگو که به صورت طبقهای (ترتیبی یا اسمی) ایجاد شدهاند، مدل رگرسیونی برای پیشبینی مقدار متغیر پاسخ (عددی - مقیاس) ایجاد شود.
هدف رگرسیون طبقه ای با مقیاس بهینه، توصیف رابطه بین متغیر پاسخ (Response) و مجموعهای از متغیرهای پیشگو (Predictive) است. با بدست آوردن یک مدل توسط رگرسیون طبقهای با مقیاس بهینه، میتوان رابطه بین متغیر پاسخ را با ترکیبهای مختلف از سطوح متغیرهای پیشگو مشخص کرد.
در این نوشتار براساس یک فایل نمونه به نام carpet.sav که در مجموعه فایلهای آموزشی SPSS نیز وجود دارد، رگرسیون طبقه ای با مقیاس بهینه در SPSS یا Optimal Scaling را به کار میبریم. البته میتوانید این فایل را با قالب فشرده از اینجا دریافت کنید.
معرفی فایل آموزشی
یک شرکت علاقمند به تاسیس یک کارگاه قالیشویی است و میخواهد به عنوان یکی از برنامههای امکانسنجی، تاثیر پنج عامل را برای ترجیح استفاده از خدمات قالیشویی را مدلبندی کند. این شرکت اطلاعات مربوط به سه شرکت قالیشویی دیگر به نامهای K2r ،Glory و Bissell را دریافت کرده است و میخواهد براساس آن مدل ترجیحات مشتری را بسازد.
پنج متغیر اصلی (پیشگو) برای این موضوع طبق جدول زیر مشخص شدهاند. ترکیب بعضی از این عوامل باعث بوجود آمدن ۲۲ الگو مختلف شده است. از ۱۰ مشتری نظرخواهی شده و میزان علاقمندی به هر یک از این ترکیبها اندازهگیری شده و با میانگینگیری از امتیازات این ۱۰ مشتری، هر یک از الگوها، امتیازدهی شدهاند.
| ردیف | نام متغیر | برچسب متغیر | سطوح متغیر | شرح |
| ۱ | package | Package design | A*, B* , C* | طراحی بستهبندی |
| ۲ | brand | Brand name | K2r, Glory, Bissell | نام شرکت قالیشویی |
| 3 | price | Price | $1.19, $1.39, $1.59 | قیمت شستشو برای هر متر مربع |
| ۴ | seal | Good Housekeeping seal | No, yes | متغیر دو وضعیتی (مهر خانهدار خوب) |
| ۵ | money | Money-back guarantee | No, yes | تضمین بازگشت پول در صورت نارضایتی |
| 6 | pref | Preference | 1 to 22 | میانگین امتیاز ۱۰ مشتری |
همانطور که مشخص است متغیرهای ردیف ۱ تا ۵، به عنوان متغیرهای پیشگو به کار رفته و متغیر pref نیز نقش متغیر پاسخ را ایفا میکند. هر چه مقدار متغیر pref کمتر باشد، نشانگر برتری الگوی به کار رفته است زیرا این متغیر نشانگر رتبه ترکیب خدمات ارائه شده است.
تصویر زیر اطلاعات مربوط به متغیرهای موجود در این فایل را نشان میدهد.
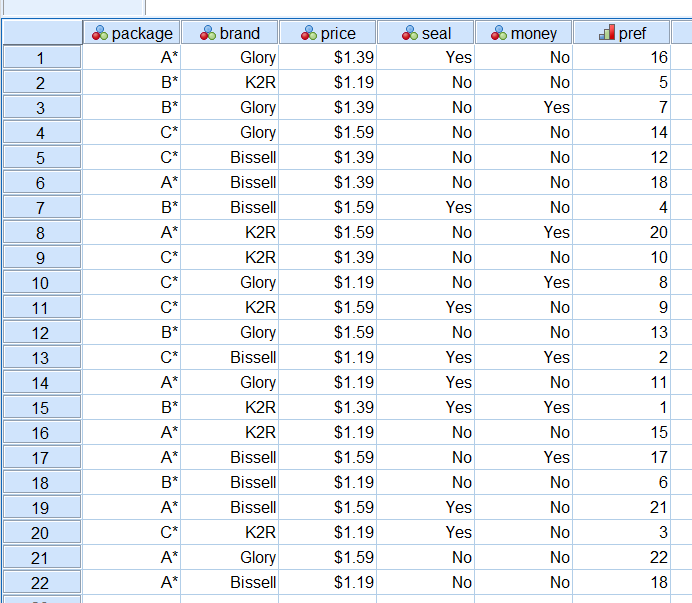
اجرای رگرسیون طبقه ای با مقیاس بهینه در SPSS
زمانی که با متغیرهای پیشگو از نوع طبقهای مواجه هستیم، اجرای رگرسیون به دو حالت صورت میگیرد. اگر بتوان یک رابطه خطی بین متغیرهای پیشگو و متغیر وابسته ایجاد کرد، مدل رگرسیون خطی مناسب است. این شیوه ایجاد مدل رگرسیونی در نوشتار رگرسیون خطی با متغیرهای طبقه ای در SPSS — راهنمای گام به گام مورد بحث قرار گرفته است. ولی اگر یک رابطه غیرخطی بین متغیرهای پیشگو طبقهای و متغیر وابسته وجود داشته باشد، بهترین گزینه برای مدلسازی، رگرسیون طبقه ای بامقیاس بهینه یا همان Optimal Scaling است.
اگر در رگرسیون خطی با متغیرهای طبقهای، نمودار مربوط به باقیماندههای استاندارد شده برحسب مقادیر متغیر پیشگوی استاندارد شده رسم شود، باید الگو مشخص مشاهده نشود. در غیر اینصورت به نظر میرسد که با افزایش یا کاهش مقدار متغیر مستقل، باقیماندهها نیز افزایش یا کاهش دارند. وجود مشکل ناهمواریانسی را نشان داده یا موید این امر است که باید از یک مدل غیرخطی یا رگرسیون Optimal Scaling استفاده کرد.
برای مثال در تصویر زیر باقیماندههای مدل رگرسیون خطی را با توجه به متغیر Package design ترسیم کردهایم. این نمودار به خوبی شکل U را نشان میدهد. در نتیجه به نظر میرسد که باید با تغییر مقیاس، ناهمواریانسی را از بین ببریم.
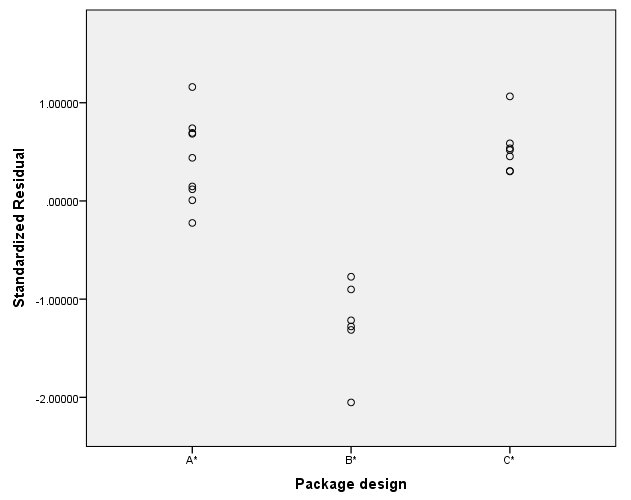
برای اجرای رگرسیون طبقهای مقیاس بهینه از فهرست Analysis گزینه Regression و دستور $$Optimal Scaling (Catereg)...$$ را اجرا میکنیم.
قرارگیری متغیرهای مربوط به مدل نیز طبق تصویر زیر صورت میگیرد.
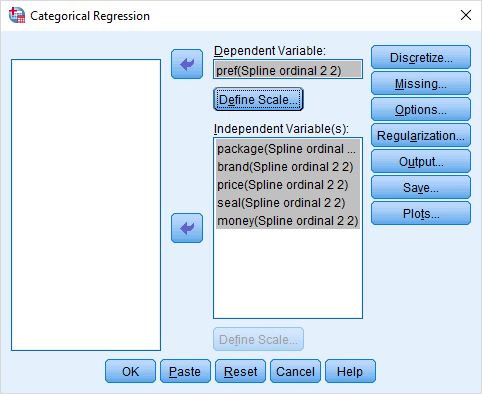
توجه داشته باشید که متغیر pref با استفاده از میانگینگیری از رتبههای مشتریان ساخته شده و باید مقیاس آن به صورت عدد باشد. در نتیجه با استفاده از دکمه Define Scale آن را تغییر مقیاس میدهیم.
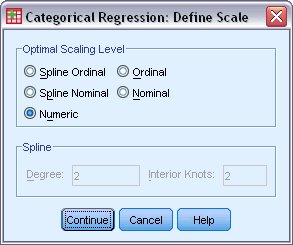
البته از آنجایی که مقیاس متغیرهای پیشگو نیز از ابتدا به درستی تعیین شده است، آنها را براساس Numeric مقیاسبندی میکنیم. به این ترتیب پنجره انتخاب متغیرها در رگرسیون Optimal Scaling به صورت زیر در خواهد آمد. فقط توجه داشته باشید که متغیر package را به مقیاس Nominal تبدیل کنید.
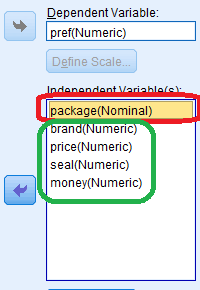
برای نمایش تحلیلها و ضرایب مدل رگرسیونی با فشردن دکمه Output، پنجره تنظمیات را ظاهر کرده و گزینهها را مطابق با تصویر زیر انجام دهید.
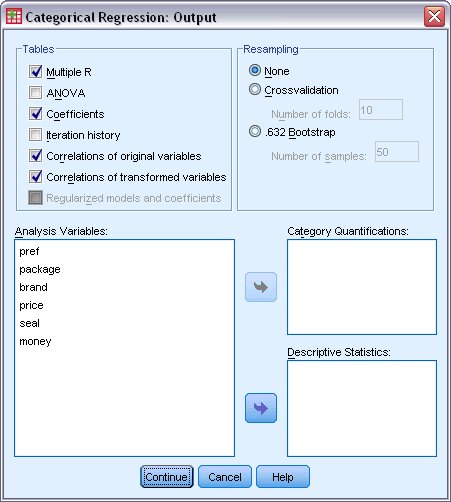
با انتخاب گزینه Multiple R مقدار ضریب تعیین محاسبه شده و ظاهر میشود. همچنین Coefficients نیز مقدار ضرایب مدل رگرسیونی را برای هر یک از متغیرهای پیشگو نمایش میدهد. انتخاب هر یک از گزینههای Correlations of original variables و correlations of transformed variables، ضریب همبستگی بین متغیر پاسخ و متغیرهای پیشگو را در حالت عادی و تغییر مقیاس یافته، محاسبه و نمایش میدهد.
برای بازگشت به پنجره اصلی از دکمه Continue استفاده کنید. همچنین برای ظاهر شدن مقادیر پیشبینی شده توسط مدل از دکمه Save استفاده کرده و تنظیمات را مطابق با تصویر زیر انجام دهید.
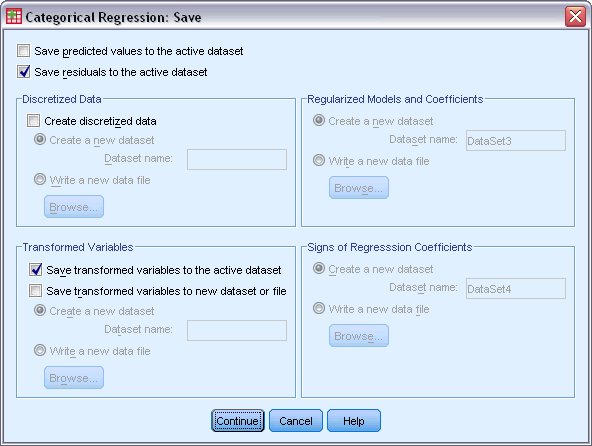
با فشردن دکمه Continue و بازگشت به پنجره اصلی، دکمه Plot را کلیک کرده تا نمودارهای لازم برای تحلیل رگرسیون طبقه ای با مقیاس بهینه را مشخص کنید. در پنجره ظاهر شده، نمودارها مربوط به متغیرهای نوع بستهبندی (Package) و قیمت (Price) را مشخص کردهایم زیرا به نظر میرسد که این دو متغیر بیشترین تاثیر را در نظر مشتری داشته باشند.
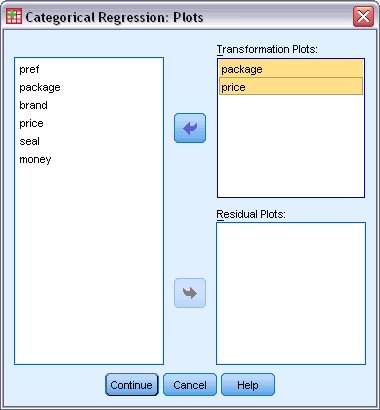
پس از بازگشت از این پنجره به پنجره اصلی رگرسیون، دکمه OK را کلیک کنید تا خروجی ظاهر شود.
نکته: اگر میخواهید این دستورات و گزینهها را در محیط Syntax و کدنویسی SPSS به کار ببرید کافی است از کد زیر استفاده کنید.
1CATREG VARIABLES=pref package brand price seal money
2 /ANALYSIS=pref(LEVEL=NUME) WITH package(LEVEL=NOMI) brand(LEVEL=NUME) price(LEVEL=NUME)
3 seal(LEVEL=NUME) money(LEVEL=NUME)
4 /MISSING=pref(LISTWISE) package(LISTWISE) brand(LISTWISE) price(LISTWISE) seal(LISTWISE)
5 money(LISTWISE)
6 /MAXITER=100
7 /CRITITER=.00001
8 /PRINT=R COEFF OCORR CORR ANOVA
9 /INITIAL=NUMERICAL
10 /PLOT=TRANS(package price)(20)
11 /SAVE=TRDATA RES
12 /REGULARIZATION=NONE
13 /RESAMPLE=NONE.تفسیر خروجی رگرسیون طبقه ای با مقیاس بهینه در SPSS
در خروجی، ابتدا توضیحاتی در مورد تعداد مشاهدات و مقادیر گمشده توضیح داده شده، سپس قسمت اصلی خروجی طبق درخواست شما، ظاهر میشود. همانطور که در گزینههای مربوط به Output مشخص کردید، ضریب همبستگی متغیرهای پیشگو، قبل و بعد از تغییر مقیاس ظاهر شدهاند.
همبستگی قبل و بعد از تبدیل
در ادامه با قسمت اول خروجی رگرسیون طبقه ای بامقیاس بهینه آشنا میشویم. ابتدا ضرایب همبستگی بین متغیرها پیشگو به همراه مقادیر ویژه (Eigenvalue) آنها دیده میشود.
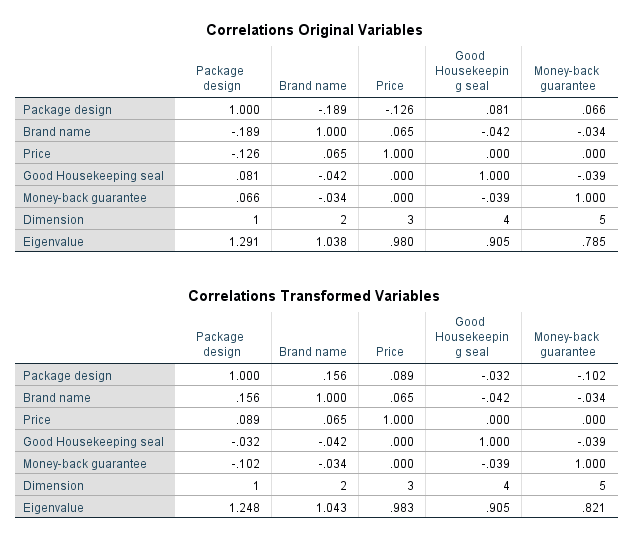
واضح است که ضریب همبستگی هر متغیر با خودش برابر با ۱ است. به همین علت قطر اصلی این جدولها، همگی دارای مقدار ۱ هستند. این جدول نشان میدهد که مشکل همخطی در بین متغیرهای پیشگو وجود ندارد زیرا در اکثر مواقع میزان همبستگی نامحسوس است.
از طرفی ضریب تعیین یا همان R Square به عنوان ملاکی برای صحت مدل رگرسیونی نیز در جدول بعدی ظاهر شده است. همانطور که مشاهده میشود، تقریبا حدود ۹۵ درصد از تغییرات متغیر پاسخ توسط مدل رگرسیونی طبقه ای با مقیاس بهینه توصیف شده است. همچنین جدول تحلیل واریانس ANOVA نیز گواهی دیگر بر مناسب بودن مدل رگرسیونی است.
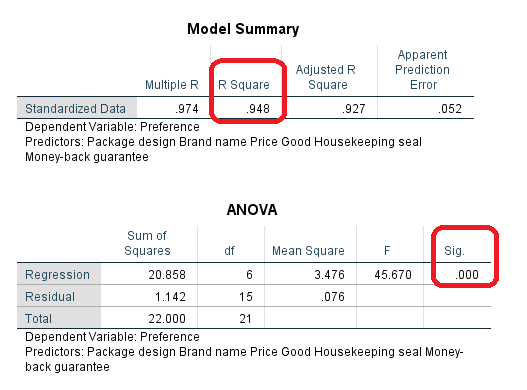
ضرایب مدل رگرسیونی
در جدول بعدی ضرایب استاندارد شده مدل رگرسیونی برای هر یک از متغیرهای پیشگو دیده میشود. در رگرسیون طبقهای هر یک از متغیرها ابتدا استاندارد شده سپس در مدل رگرسیونی به کار میروند به همین دلیل فقط ضرایب استاندارد شده ظاهر شدهاند.
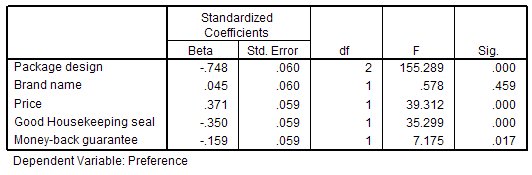
بر طبق این جدول و با توجه به ستون Sig، مشخص است که متغیر Brand name برای مشتریان مورد توجه نیست و ملاکی برای رتبهبندی خدمات قالیشویی محسوب نمیشود. زیرا مقدار Sig=0٫456 از مقدار خطای ۵٪ بزرگتر است در نتیجه فرض صفر بودن این ضریب تایید میشود. به بیان دیگر این آزمون نشان میدهد که اگر متغیر Brand name از مدل حذف شود، تغییر محسوسی در مقدار پیشبینی برای متغیر پاسخ بوجود نخواهد آمد.
نکته: توجه داشته باشید که بزرگ بودن مقدار Sig نشانگر بیتاثیر بودن آن متغیر نسبت به وجود بقیه متغیرها در مدل است. بنابراین نباید همه متغیرهایی که دارای مقدار Sig بزرگتر از ۵٪ هستند را یکجا از مدل حذف کرد. این کار باید به صورت یک به یک انجام شود تا مدل فقط تحت تاثیر مهمترین متغیرها و البته تعداد متغیرهای بهینه ساخته شود.
بزرگترین مقدار ضریب استاندارد، مربوط به متغیر Package design است، پس مهمترین متغیر در پیشگویی انتظار مشتریان از شرکت قالیشویی نوع بستهبندی است. سپس متغیرهای price و Good Housekeeping seal به عنوان متغیرهای مهم در نظر گرفته میشوند. در آخرین مرتبه نیز متغیر گارانتی بازگشت پول (Money-back guarantee) قرار گرفته است.
نکته: توجه دارید که در اینجا برای مقایسه اهمیت متغیرها از قدر مطلق ضریب استاندارد استفاده میکنیم.
تعیین اهمیت متغیرهای پیشگو
برای تشخیص اهمیت هر یک از متغیرهای پیشگو و ارتباط آنها با متغیر پاسخ بهتر است به ضریب همبستگی مرتبه صفر، ضریب همبستگی جزئی و بخشی نیز توجه کنیم. در جدول بعدی در خروجی این محاسبات صورت گرفته است.
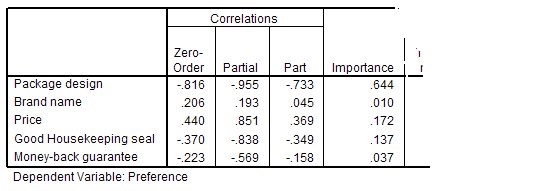
ضریب همبستگی مرتبه صفر، میزان همبستگی متغیرهای پیشگو را عرض از مبدا در مدل رگرسیونی را نشان میدهند. همچنین ضریب همبستگی جزئی و بخشی (نیمه جزئی) نیز با حذف اثر متغیرهای دیگر روی متغیر پیشگو و متغیر پاسخ، ضریب همبستگی را محاسبه میکنند. با این تفاوت که در ضریب همبستگی نیمه جزئی یا بخشی، اثر متغیرهای دیگر فقط از متغیر پاسخ حذف میشود.
برای درک بهتر این ضرایب بهتر است مطلب ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده را مطالعه کنید.
همچنین برای نمایش اهمیت هر یک از متغیرهای پیشگو در مدل رگرسیونی، از «میزان اهمیت» (Importance) یا «اندازه پرات» (Pratt's measure) کمک میگیرند. میزان اهمیت براساس حاصلضرب مقادیر ضریب همبستگی مرتبه صفر با ضرایب هر یک از متغیرهای مدل رگرسیونی بدست میآید. اگر این حاصلضربها را با ضریب تعیین (R Square) جمع کرده و نتیجه را بر ضریب تعیین تقسیم کرده و از حاصل یک واحد کم کنیم، ضریب اهمیت بدست میآید.
همانطور که در ستون Importance دیده میشود، متغیر Package design بیشترین تاثیر را روی متغیر پاسخ (Pref) دارد. در گام بعدی متغیرهای Price و Good Housekeeping seal و در آخر هم متغیر Brand name قرار گرفته است. از طرفی متوجه میشویم که دو متغیر Package design و Price روی هم، دارای اهمیتی برابر با 0٫654 هستند و متغیرهای Package design و Price به همراه Good Housekeeping seal حدود ۹۵ درصد در تشکیل مدل اهمیت دارند.
نکته: برعکس ضریب اهمیت متغیرهای پیشگو در مدل رگرسیون خطی، در رگرسیون طبقه ای با مقیاس بهینه امکان جمع کردن ضرایب اهمیت وجود دارد. همانطور که در توضیحات بالا دیده شد، اهمیت هر یک از متغیرها را با متغیرهای دیگر میتوان جمع کرد و اهمیت کل را نشان داد.
بررسی همخطی چندگانه
وجود همبستگی بین متغیرهای پیشگو یکی از مشکلاتی است که در ممکن است مدل رگرسیون خطی با حداقل مربعات معمولی (OLS) وجود داشته باشد. وجود همخطی (Multicollinearity) را به کمک بررسی مقادیر «شاخص تحمل» (Tolerance) یا «عامل تورم واریانس» (Variance Inflation Factor) شناسایی کرد. با وجود همخطی، پایداری مدل کاهش مییابد به این معنی که با تغییر تعداد کمی از مقادیر، پارامترهای مدل دچار تغییرات زیاد میشوند. به این ترتیب مدل قابل اعتماد نخواهد بود و از نمونهای به نمونه دیگر متفاوت خواهد شد.
برای بررسی مشکل همخطی چندگانه در رگرسیون طبقه ای با مقیاس بهینه از «شاخص تحمل» (Tolerance) استفاده میشود. این شاخص نشان میدهد که میزان ارتباط خطی بین یک متغیر پیشگو با متغیرهای دیگر چقدر است. در اینجا «مقدار تحمل» برای هر یک از متغیرهای پیشگرو متناسب با واریانس مقادیر پیشبینی شده برای متغیر پاسخ توسط مدل رگرسیونی است زمانی که متغیرهای پیشگو دیگر در مدل حضور نداشته باشد.
اگر «مقدار تحمل» نزدیک به یک باشد، بیانگر عدم ارتباط خطی بین آن متغیر با متغیر پیشگوی دیگر است و برعکس اگر مقدار تحمل به صفر نزدیک شود، نشانگر آن است که میزان اطلاعاتی که متغیر پیشگو از متغیر پاسخ به همراه دارد کم بوده و بهتر است از مدل حذف شود. در حقیقت بیشتر اطلاعاتی که توسط این متغیر در مدل ارائه میشود به علت وجود رابطه با متغیرهای دیگر است.
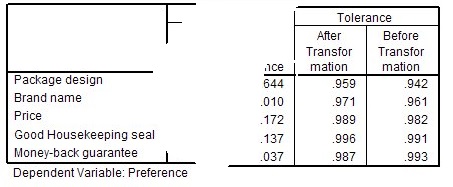
همانطور که در جدول بالا مشاهده میکنید، همه متغیرها دارای «مقدار تحمل» نزدیک به یک هستند در نتیجه در این مدل با مشکل همخطی مواجه نیستیم.
تغییر مقیاس متغیرهای طبقه ای
رسم مقادیر متغیرهای اصلی در برابر تغییر مقیاس یافته آنها میتواند شامل چند نوع روند باشد. این نمودارها به نام «نمودارهای تبدیلها» (Transformation Plot) معروف هستند. در ادامه نمودارهایی که مربوط به متغیر قیمت و تبدیل یافته آن است ترسیم شده است.
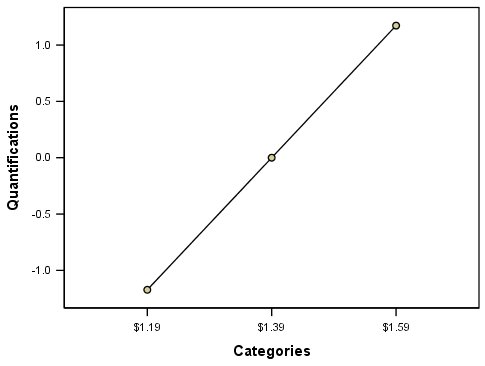
متغیرهایی که به صورت عددی بوده و با استفاده از تبدیل دچار تغییر مقیاس شدهاند باید ساختار اصلی در دادهها را حفظ کنند. به همین دلیل رسم نمودار برای این متغیرها باید منجر به نمایش یک خط راست شود. به این معنی که برای متغیرهای عددی، تغییر مقیاس باید حافظ ترتیب باشد و فاصله بین دو مقدار در حالت اصلی باید در حالتی که تبدیل صورت گرفته نیز حفظ شود.
در نمودار بالا، متغیر Price و تبدیل یافته آن ترسیم شده است. همانطور که مشخص است، این تبدیل به صورت یک به یک (One to One) بوده و نتیجه ترسیم نمودار یک خط راست است. بنابراین تغییر مقیاس برای متغیر طبقهای Price باعث جابجایی یا تغییر ترتیب مقادیر نشده است. در حقیقت فاصله بین سطوح متغیر Price در هر دو حالت اصلی و تبدیل یافته حفظ شده. اگر برای متغیرهای ترتیبی یا اسمی، نموداری به این شکل ساخته شود، بهتر است از تبدیل عددی (Number) استفاده شود.
برای متغیرهای ترتیبی، فاصله بین مقادیر حفظ نشده ولی ترتیب آنها حتما باید در حالت عادی و تبدیل یافته حفظ شود. به این ترتیب نمودار رسم شده برای چنین متغیرهایی باید حتما دارای روند صعودی باشد، حتی اگر نمودارشان به شکل یک خط در نیاید ولی منحنی ترسیم باید شکل یک تابع صعودی را داشته باشد. این امر نشان میدهد که ترتیب مقادیر در هر دو حالت تغییری نیافته است. از آنجایی که در تبدیلات از حالت ترتیبی (Ordinal) استفاده نشده، نموداری برای نمایش وجود ندارد. اگر برای متغیر عددی (Number) چنین نموداری حاصل شود، بهتر است آن را با تبدیل ترتیبی (Ordinal) مورد سنجش قرار دهیم.
در نمودار زیر، متغیر Package design را در دو حالت تبدیل یافته و اصلی ترسیم کردهایم. از آنجایی که تبدیل برای این متغیر را از نوع اسمی (Nominal) انتخاب کردیم، روند خاصی برای جابجایی مقادیر روی نمودار نمیتوان تصور کرد.
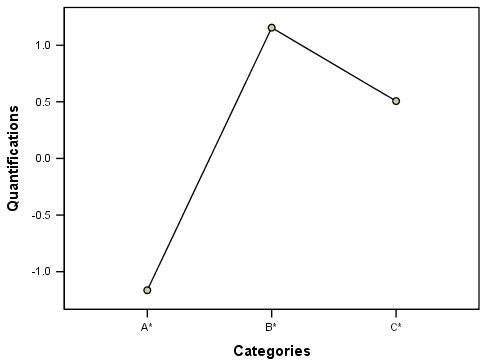
همانطور که در نمودار بالا مشاهده میکنید، روی محور افقی، ترتیب مقادیر براساس ترتیب مشاهدات است. ولی این ترتیب برای محور افقی تغییر یافته است زیرا تغییر مقیاس، مقادیر آن را ساخته است. این نمودار میتواند به شکل خطی (Linear) و حتی غیر خطی (Nonlinear) باشد. اگر روند صعودی در این نمودار ظاهر شود، بهتر است از تبدیل ترتیبی (Ordinal) برای چنین متغیری استفاده شود.
مشکل ناهمواریانسی
همانطور که در ابتدای متن اشاره کردیم، ترسیم مقادیر متغیر پاسخ یا باقیماندههای مدل بر حسب متغیر پیشگو، مشکل ناهمواریانسی را نشان میدهد. اگر با افزایش یا کاهش مقدار متغیر پاسخ، واریانس متغیر وابسته افزایش یابد، مشکل ناهمواریانسی وجود دارد. زیر از فرضهای اولیه مدل رگرسیونی، همواریانسی متغیر پاسخ در سطوح مختلف متغیرهای پیشگو است.
همچنان که دیدید، در صورت وجود مشکل ناهمواریانسی، نمودار ترسیم شده برای متغیر پاسخ برحسب متغیرهای طبقهای به صورت یک U در خواهد آمد. در اینجا میخواهیم براساس مدل تشکیل شده توسط رگرسیون طبقه ای با مقیاس بهینه این موضوع را بررسی کنیم.
از آنجایی که متغیر Package design بیشترین نقش و ارتباط را با متغیر پاسخ دارد، از آن استفاده خواهیم کرد. برای رسم چنین نموداری از دستور Chart Builder و نمودار Scatter/Dot کمک میگیریم. مطابق با تصویر زیر، در محور افقی متغیر Package design Quantification را قرار داده و باقیمانده (Residual) را هم در محور عمودی ظاهر میکنیم.
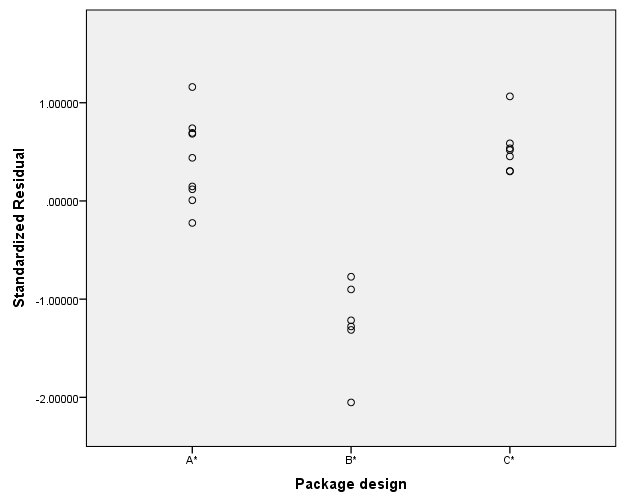
نکته: از آنجایی که در هنگام اجرای رگرسیون طبقهای با مقیاس بهینه، گزینه save residual را از پنجره Options انتخاب کرده بودیم، باقیمانده به عنوان یک متغیر جدید در بیان متغیرها در کادر Variables با برچسب residuals و نام RES_1 دیده میشود. همچنین مقادیر متغیرهای پاسخ و پیشگو تبدیل یافته نیز با اسامی TRA1_1 تا TRA1_6 در این لیست قرار دارند. در ضمن متغیر Package design تبدیل یافته نیز با نام TRA1_2 و برچسب Package design Quantification مشخص شده است.
با فشردن دکمه OK خروجی و نمودار رسم شده به صورت زیر درخواهد آمد.
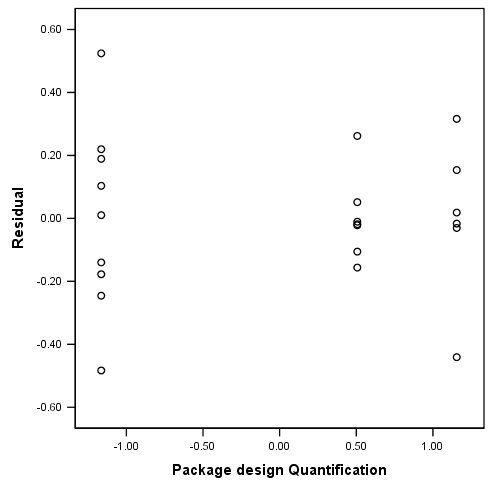
همانطور که در نمودار بالا مشخص است، الگو U شکل در آن دیده نمیشود. در نتیجه مشکل همواریانسی که ناشی از اجرای رگرسیون خطی چندگانه روی این مجموعه داده بود در این روش رگرسیونی وجود ندارد و به نظر میرسد که واریانس باقیماندهها وابسته به مقادیر متغیر پیشگو نیست.
خلاصه و جمعبندی
در این نوشتار به بررسی یک روش رگرسیون غیر خطی پرداختیم که در آن متغیرهای طبقهای به عنوان متغیر پیشگو به کار رفته و با تغییر مقیاس به حالت بهینه در مدل رگرسیونی در میآیند. برای انجام محاسبات از تابع CATREG در spss استفاده کردیم و خروجیهای حاصل را بررسی و تفسیر نمودیم. استفاده از رگرسیون طبقه ای با مقیاس بهینه در زمانی که متغیرهای طبقهای دارای مشکل همخطی هستند بسیار مفید است و تبدیل مناسب روی آنها باعث از بین رفتن ایراداتی میشود که اغلب در رگرسیون خطی وجود دارد.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- آموزش همبستگی و رگرسیون خطی در SPSS
- مجموعه آموزشهای داده کاوی و یادگیری ماشین
- ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها
- آموزش رگرسیون — مجموعه مقالات جامع وبلاگ فرادرس
- رگرسیون غیر خطی در R — به زبان ساده
^^










