رویه های درجه دوم – به زبان ساده
پیشتر در وبلاگ فرادرس مفاهیم مربوط به رسم خطوط و صفحات فضایی را بیان کردیم. در این مطلب قصد داریم تا یک قدم فراتر گذاشته و انواع رویه های درجه دوم را توضیح دهیم.


شکل کلی رویه های درجه دوم
رویه در ریاضیات به رابطهای اشاره دارد که نشان دهنده سطحی سهبعدی است.
هدف ما در این مطلب توضیح نحوه ترسیم رویههای درجه دوم است. رابطه کلی یک رویه درجه دوم به صورت زیر است.
در رابطه فوق A تا J ضرایب ثابتی هستند که اندازه آنها نشان دهنده شکل رویه خواهد بود. در ادامه دستهبندیهای مختلف این رویهها را با توجه به شکل مختلف معادلات، معرفی خواهیم کرد.
بیضی گون
همانطور که در مطلب بیضی نیز بیان شد، شکل کلی یک بیضی دوبعدی به صورت زیر است.
با اضافه کردن متغیر سوم، به رابطهای میرسیم که پوستهای بیضی گون را توصیف میکند. در نتیجه رابطه یک بیضی گون به صورت زیر است.
شکل پوسته رابطه فوق نیز به صورت زیر است.
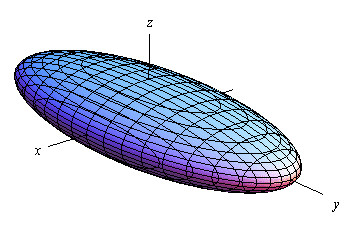
بدیهی است که اگر در رابطه بیضی گون مقادیر a و b و c با هم برابر باشند، رابطه مربوط به کره بدست خواهد آمد.
مخروط
رابطه کلی نشان دهنده یک مخروط به صورت زیر است.
شکل چنین مخروطی نیز در ادامه ارائه شده است.
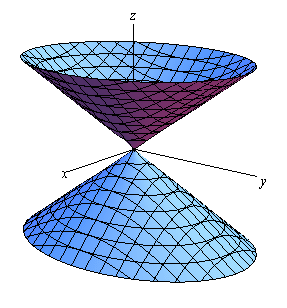
توجه داشته باشید که جهت مخروط همواره به سمت متغیر سمت راست رابطه فوق است (برای نمونه در شکل بالا مخروط در راستای z قرار گرفته). تصویر فوق، نشان دهنده شکل یک ساعت شنی است. حال این سوال مطرح میشود که رابطه مخروط را به چه صورت بنویسیم تا فقط بخش بالا یا پایین آن را نشان دهد؟ بدین منظور معادله اصلی را به صورت زیر بر حسب z مینویسیم.
بنابراین رابطه مربوط به بخش بالای مخروط به صورت و بخش پایین مخروط به صورت است. به همین صورت رابطه مربوط به مخروطی که در راستای محور x قرار گرفته به صورت زیر خواهد بود.
استوانه
رابطه عمومی توصیف کننده یک استوانه به صورت زیر است.
رابطه فوق نشان دهنده استوانهای با مقطع بیضی است. شکل زیر رویه مذکور را نشان میدهد.
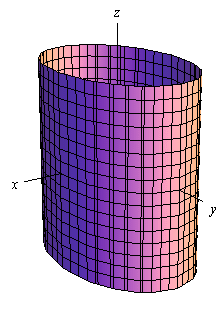
اگر در رابطه استوانه a=b باشد، مقطع استوانه بدست آمده، به صورت دایره خواهد بود. معمولا در این صورت رابطه را به صورت زیر نمایش میدهند.
هذلولی یکپارچه
رابطه زیر هذلولی یکپارچه را نشان میدهد که در راستای z قرار گرفته است.
همچنین در ادامه شکل مربوط به رابطه فوق ترسیم شده است.
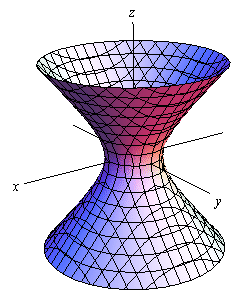
متغیری که جلوی آن علامت منفی قرار گرفته جهت هذلولی گون را نشان میدهد.
هذلولی دو پارچه
در ادامه رابطه مربوط به یک هذلولی گون دو پارچه ارائه شده است.
شکل مرتبط با رابطه فوق نیز به صورت زیر است.
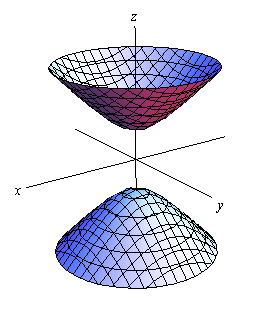
در حالت دو پارچه، متغیری که علامت جلوی آن مثبت است، محور هذلولی را نشان میدهد.
سهمی گون بیضوی
در ادامه رابطه مربوط به یک سهمی گون بیضوی ارائه شده است.
همانند استوانه در این حالت نیز مقطع سهمی گون بیضوی در حالتی که a=b باشد، به صورت دایره خواهد بود. در شکل زیر یک سهمی گون بیضوی نشان داده شده است.
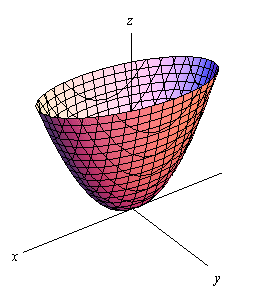
در این حالت متغیری که توان آن ۱ است، نشان دهنده جهت سهمی گون است.
سهمی هذلولی گون
در ادامه رابطه مربوط به سهمی هذلولی گون نشان داده شده است.
همچنین شکل مربوط به رابطه فوق در زیر ترسیم شده است.
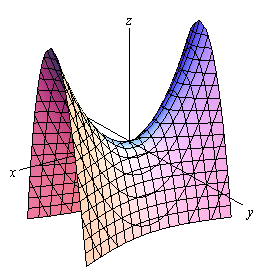
توجه داشته باشید که در دو مورد آخر علامت c نشان دهنده جهت رو به بالا یا رو به پایین رویه است. برای نمونه رویه زیر را در نظر بگیرید.
با توجه به علامتهای متغیرها میتوان دید که رابطه فوق نشان دهنده یک سهمی گون بیضوی است. از طرفی علامت c در رابطه فوق منفی بوده بنابراین جهت رویه به سمت پایین خواهد بود. همچنین با فرض x,y=0 مقدار z=۶ بدست میآید. بنابراین رویه فوق به صورت زیر است.
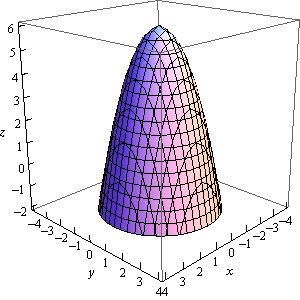
توصیه میکنیم مثالهای ارائه شده در ادامه را مطالعه فرمایید.
مثال ۱
رویه مربوط به رابطه زیر را ترسیم کنید.
در ابتدا مشاهده میکنید که یک متغیر در رابطه موجود نیست. بنابراین رابطه فوق استوانهای با مقطع بیضی را نشان میدهد. در ادامه شکل این رویه نشان داده شده.
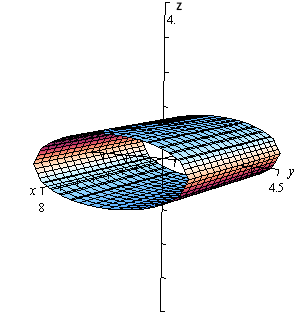
مثال ۲
رویه زیر به چه شکل است؟
همانطور که میبینید توان z از درجه اول بوده و دو متغیر هم علامت هستند. بنابراین این رابطه نشان دهنده یک سهمی گون بیضوی است. از طرفی ضریب c (مخرج z) نیز مثبت است. بنابراین جهت رویه به سمت بالا خواهد بود. در نهایت شکل این رویه به صورت زیر است.
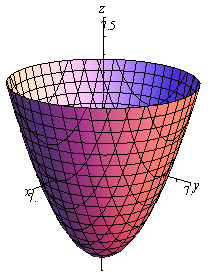
این مطلب را میتوانید در یک نگاه، با استفاده از جدول زیر فرا گیرید.
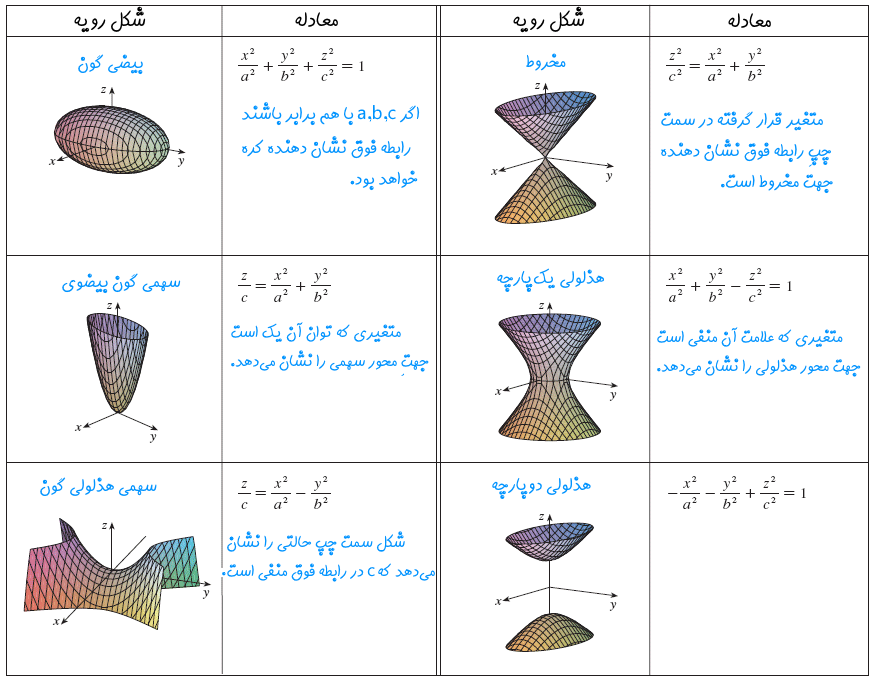













خیلی متشکر و ممنون
سلام مهندس وقتتون بخیر
اگه سوالی داشته باشیم که «مقدار x و y را طوری قرار دهید که معادله بیضوی، هذلولوی و سهمی بشه» باید چیکار کنیم؟ منظورم اینه که روش حل به چه صورت هستش؟
سلام ، ببخشید من معادله سهمی هذلولی گون رو تو geo gebra میزنم یه چیز دیگه نشون میده بعد وقتی معادله به فرم x^2+y^2 مینویسم سهمی هذلولی گون نشون میده …. میشه لطفا توضیح بدید مشکلش از کجاست؟
سلام
خسته نباشید
تو سهمی گون بیضوی، اگر علامت aوb منفی باشه، شکل برعکس میشه؟
سلام
در جواب مثال 2 بیان کردید معادله مربوط به یک سهمی بیضی گون اما مخرج های کسرهای 2^x و2^ y برابر هستند(برابر 4) و معادله مربوط به سهمی گون دایروی
سلام.
سهمیگون دایرهای نوع خاصی از سهمیگون بیضوی است که در آن، a=b است. بنابراین، اگر به این رویه بگوییم سهمیگون بیضوی اشتباه نیست.
موفق باشید.
با سلام
خدا خیرتون بده
واقعاً عالی
بسیار عالی بود. مچکرم
اگر یک سهمی گون داشته باشیم سطح بالای اون چیه؟
(منظورم اینه وقتی از بالا نگاه میکنیم چیه؟)
با سلام و وقت بخیر؛
اگر منظورتان تصویر سهمیگون بر روی یک سطح دوبعدی (مثل صفحه x-y) است، این تصویر به معادله سهمیگون بستگی خواهد داشت. با توجه به این موضوع، تصویر دوبعدی سهمیگون میتواند به شکل دایره یا بیضی باشد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام z^-y^=1 و 1=yz به چه شكلي هستن؟
واقعا مطالب خیلی مفید بودن ممنون????
واقعا متشکرم. عالی بود
بزن جئو جبرا
تمام مدرس های فرادرس یه طرف جناب امید زندی یه طرف.من خودم دبیرم و شیوه ی تدریس جناب زندی رو عالیترین میدونم مضاف بر اینکه صداشون هم برای تدریس فوق العاده رسا هست
بطور کل از فرادرس متشکریم
سلام مهندس در مثال ۱مگه فرمول بصورت دو بعدی نیست؟(فرمول یک بیضی هست) ،پس چرا شکل مربوط بهش سه بعدیه(استوانه) ؟
با سلام؛
در نوشتن معادله از دو متغیر استفاده شده است؛ این امر نشان میدهد که شکل دوبعدی این معادله، مقطعی از رویه سهبعدی است. از این رو برای رسم این معادله در سه بعد کافی است مقطع دوبعدی را در راستای متغیر سوم توسعه دهید.
سلام
واااااقعا عالی بود مرسی
مرسی دستتون درد نکنه عالی بود فقط کاش بیشتر مثال میزدید و طریقه رسمش رو هم مینوشتید ولی در کل مرسی
سلام وقتتون بخیر معادله (x^2+y^2=z^2)
معادله چه شکلی است؟