تحلیل MANOVA‌ در پایتون – راهنمای کاربردی

در نوشتارهای قبلی به بررسی چند روش تحلیل واریانس پرداختیم. به عنوان مثال، تحلیل واریانس یک طرفه، دو طرفه و تحلیل واریانس با داده‌های تکراری از مواردی بود که مورد بررسی قرار گرفت و کدهای مربوط به انجام این گونه تحلیل‌ها در پایتون معرفی گردید و خروجی‌های حاصل نیز تفسیر شد. روش دیگری از تحلیل واریانس وجود دارد که در آن متغیر پاسخ، چند متغیر کمی است یا به نوع می‌توان آن را یک متغیر چند بُعدی در نظر گرفت. در این وضعیت پاسخ را به صورت چند متغیره مشخص کرده و به صورت یک ماتریس نشان می‌دهند. به این ترتیب تحلیل چند متغیره واریانس صورت می‌گیرد که اغلب با (MANOVA (Multivariate Analysis of Variance نشان داده می‌شود. در این نوشتار با تحلیل MANOVA‌ در پایتون آشنا خواهیم شد.

هنگام انجام تحلیل MANOVA هر جا احتیاج به انجام محاسبات باشد، از کدهای زبان برنامه‌نویسی پایتون و کتابخانه‌های آن استفاده خواهیم کرد. ابتدا در مورد شیوه تجزیه واریانس در تحلیل چند متغیره صحبت کرده و سپس محاسبات را به کمک یک مثال در پایتون پیاده‌سازی می‌کنیم.

به منظور آشنایی بیشتر با مفاهیم اولیه در مورد تحلیل واریانس بهتر است مطلب تحلیل واریانس (Anova) — مفاهیم و کاربردها و آنالیز واریانس (ANOVA) یک و دو طرفه در R — راهنمای کاربردی را بخوانید. همچنین مطالعه نوشتار متغیر فاکتور (Factor) یا متغیر عامل در R — راهنمای کاربردی خالی از لطف نیست.

تحلیل MANOVA‌ در پایتون

همانطور که در مورد تحلیل واریانس آموختیم، مشخص است که در تحلیل MANOVA نیز، هدف ایجاد یک مدل یا کشف ارتباط بین متغیرهای عامل (فاکتور) با یک یا چند متغیر کمی (پیوسته) است. در حقیقت تحلیل MANOVA گسترش یافته و تعمیمی بر تحلیل واریانس یک یا دو طرفه محسوب می‌شود. ابتدا بهتر است منظور از MANOVA‌ را درک می‌کنیم.

تحلیل MANOVA چیست؟

در نوشتارهای تحلیل واریانس دو طرفه در پایتون --- راهنمای گام به گام و تحلیل واریانس یک طرفه در پایتون --- راهنمای گام به گام خواندید که تکنیک تجزیه واریانس به منظور مقایسه میانگین بین دو یا چند جامعه برحسب یک یا چند متغیر عامل، به کار می‌رود. شاید این طور به نظر برسد که برای مقایسه چند میانگین در بین چندین جامعه نیز بتوان از ترکیب و تکرار چند بار تحلیل واریانس یک طرفه یا دوطرفه نیز به نتیجه رسید. ولی به یاد داشته باشید که این امر باعث افزایش میزان خطای کل آزمون خواهد شد.

اغلب برای مقایسه میانگین بین دو جامعه تحت یک عامل یا فاکتور با دو سطح از آزمون T‌ استفاده می‌شود. شاید اینطور به نظر برسد که برای مقایسه میانگین بین چند جامعه نیز بتوان از چندین آزمون T‌ استفاده کرد. در اینجا هم مشکل افزایش خطای آزمون‌های دو تایی بود. به این ترتیب اگر به جای انجام تحلیل MANOVA، از چند تحلیل ANOVA استفاده شود، خطای ناشی از انجام آزمون‌های همزمان افزایش یافته و دقت نتایج مورد تردید قرار می‌گیرد.

بنابراین اگر تحلیل MANOVA‌ را گسترش یافته تحلیل‌های ANOVA‌ در حالت یک و دو طرفه در نظر بگیریم، می‌توان برای MANOVA نیز عبارت یک طرفه یا دو طرفه را به کار برد، به این معنی که اگر تعداد متغیرهای عامل یکی باشد، تحلیل MANOVA یک طرفه و اگر بیش از یک باشد تحلیل واریانس چند متغیره یا همان MANOVA، دو طرفه خواهد بود.

فرضیاتی که برای انجام تحلیل واریانس چند متغیره MANOVA باید در نظر گرفت، شبیه تحلیل ANOVA‌ است:

• وجود توزیع نرمال برای متغیر وابسته در هر گروه از سطوح متغیرهای عامل
• یکسان و برابر بودن ماتریس کوواریانس برای هر گروه از سطوح متغیرهای عامل (توجه داشته باشید که به جای واریانس از ماتریس کوواریانس استفاده شده است.)
• وجود رابطه خطی بین متغیر وابسته و مستقل در بین هر گروه از سطوح متغیرهای عامل

این امر نشان می‌دهد که تفاوتی که بین توزیع داده‌ها هر گروه وجود دارد فقط به تغییر میانگین وابسته است و واریانس یا پراکندگی در آن نقشی ندارد.

در تحلیل ANOVA، به کمک تجزیه مجموع مربعات اختلاف از میانگین یا به نوعی واریانس کل، به تحلیل در مورد میانگین پرداختیم. ولی در MANOVA به علت اینکه تحلیل روی داده‌های چند متغیره صورت می‌گیرد، مبنای کار تجزیه ماتریس واریانس-کوواریانس (Variance-Covariance Matrix) است که یک ماتریس معین مثبت (Positive Definite Matrix)  محسوب می‌شود. با توجه به فرضیات بالا و به کمک تجزیه ماتریس واریانس-کوواریانس قادر به انجام آزمون‌ها همزمان برای چند متغیر وابسته نسبت به متغیرهای عامل یا فاکتور هستیم.

برای مثال فرض کنید می‌خواهیم اثر رژیم غذایی را در کاهش قند، چربی و فشار خون افراد، مشخص کنیم. سه نوع رژیم غذایی (خام خواری، پروتئین و بدون قند)‌ را در نظر گرفته‌ایم. قرار است داوطلب‌ها را به سه دسته تقسیم کرده و هر یک از رژیم‌ها را به آن‌ها بدهیم. در آخر هر روز، میزان فشار خون، چربی و قند این افراد اندازه‌گیری می‌شود. می‌خواهیم تشخیص دهیم که میانگین این متغیرها وابسته به نوع رژیم است. به این معنی که نوع رژیم در تغییر میانگین مشخصات خونی افراد تاثیر گذار است یا خیر؟ از آنجایی که اثر رژیم غذایی باید همزمان روی هر سه متغیر وابسته تاثیر بگذارد، از تحلیل واریانس چند متغیره استفاده خواهیم کرد.

آماره آزمون MANOVA دارای توزیع ویشارت است و به کمک مقادیر ویژه تبدیلی از ماتریس واریانس-کوواریانس تعیین می‌شود. فرض صفر در تحلیل MANOVA‌، برابری ماتریس واریانس-کوواریانس باقی‌مانده‌ها با ماتریس حاصل از مدل است.

$$\large {\displaystyle \Sigma _{\text{model}}=\Sigma _{\text{residual}}}$$

انتظار داریم که ماتریس واریانس-کوواریانس مدل بزرگ بوده و ماتریس واریانس-کوواریانس باقی‌مانده‌ها (خطا) کوچک باشد. به این معنی که مدل بیشتر پراکندگی یا واریانس داده‌ها را توصیف کرده و سهم کوچکی برای خطا باقی مانده باشد. ماتریس به کار رفته برای محاسبات برابر است با حاصل ضرب ماتریس واریانس-کوواریانس مدل در معکوس ماتریس واریانس-کوواریانس باقی‌مانده‌ها، بنابراین خواهیم داشت.

$$\large {\displaystyle A=\Sigma _{\text{model}}\times \Sigma _{\text{res}}^{-1}}$$

مقادیر ویژه ماتریس $$A$$ در تعیین آماره آزمون MANOVA به کار می‌رود. برای مثال آماره بارتلت (Bartlett) که با $$\Lambda_{Pillai}$$‌ نشان داده می‌شود، به صورت زیر تعریف می‌شود.

$$\large {\displaystyle \Lambda _{\text{Pillai}}=\sum _{1...p}(\lambda _{p}/(1+\lambda _{p}))=\mathrm {tr} (A(I+A)^{-1})}$$

همچنین آماره ویلکس (Wilks) نیز به عنوان آماره آزمون MANOVA قابل استفاده است که به صورت زیر تعریف می‌شود.

$$\large {\displaystyle \Lambda _{\text{Wilks}}=\prod _{1...p}(1/(1+\lambda _{p}))=\det(I+A)^{-1}=\det(\Sigma _{\text{res}})/\det(\Sigma _{\text{res}}+\Sigma _{\text{model}})}$$

آماره‌های آزمون دیگر نیز وجود دارند که در تحلیل MANOVA به کار می‌روند ولی نکته مهم در همه آن‌ها استفاده از ماتریس $$A$$ است که مقادیر ویژه آن نیز به صورت $$\lambda_p$$ مشخص شده است.

ساده‌ترین آن‌ها آماره Hotelting-Lawley با نماد $$\Lambda_{LH}$$ و بزرگترین ریشه روی (Roy's geatest root) با نماد $$\Lambda_{Rpy}$$ است. شیوه محاسبه هر یک در ادامه قابل مشاهده است.

$$\large {\displaystyle \Lambda _{\text{LH}}=\sum _{1...p}(\lambda _{p})=\mathrm {tr} (A)}$$

$$\large {\displaystyle \Lambda _{\text{Roy}}=\max _{p}(\lambda _{p})=\|A\|_{\infty }}$$

نکته: اگر متغیر عامل دو سطحی باشد، همه آماره دارای توزیع مربع T یا Hoteling's T square خواهند بود.

محاسبات MANOVA در پایتون با کتابخانه statmodels

در این بخش به کمک مجموعه داده‌های گل زنبق (Iris) براساس متغیر طبقه‌ای که نوع گل را مشخص می‌کند، می‌خواهیم تغییرات در میانگین طول و پنهای گلبرگ و کاسبرگ‌ها را مورد آزمون قرار دهیم. در نتیجه نوع گل (Species) متغیر عامل با سه سطح بوده و متغیرهای بعدی (Sepal_Length, Sepal_Width, Petal_Length, Petal_Width) کمّی بوده و به عنوان متغیرهای وابسته (متغیر وابسته چند متغیره)‌ به کار خواهند رفت.

فیلم آموزش برنامه نویسی پایتون Python – مقدماتی در فرادرس

کلیک کنید

ابتدا به کمک اجرای کد زیر کتابخانه‌های مورد نیاز را بارگذاری می‌کنیم.

واضح است که کتابخانه pandas و تابع MANOVA‌ از کتابخانه statmodels فراخوانی شده‌اند. حال فایل اطلاعاتی Iris‌ را از اینترنت دریافت و بارگذاری می‌کنیم. فراموش نکنید که هنگام اجرای این دستور به اینترنت متصل باشید.

از آنجایی که در اسامی متغیرها در این فایل از علامت "."‌ استفاده شده است، باید برای استفاده در پایتون آن‌ها را به "_" تغییر دهیم. دستورات زیر به این منظور به کار گرفته شده است. البته در انتها نیز دستورات مربوط به نمایش نتیجه این تغییرات و چند سطر اول داده‌ها را مشاهده می‌کنید.

نتیجه این کارها، ایجاد یک چارچوب داده (Data frame) به صورت زیر است.

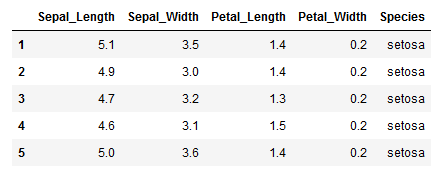
حال که مجموعه داده، آماده شده است، از تابع MANOVA استفاده کرده و تحلیل واریانس چند متغیره را به کمک معرفی مدل اجرا می‌کنیم.

همانطور که مشخص است مدل به صورت چند متغیره است و بین متغیرهای وابسته از علامت + استفاده شده است تا ماتریس واریانس-کوواریانس براساس آن‌ها تشکیل شود. متغیر عامل نیز Species است که ارتباط آن با متغیرهای وابسته با علامت ~ تعیین شده. در انتهای دستور نیز چارجوب داده df در نظر گرفته شده که حاصل از تغییرات روی مجموعه داده‌های Iris است.

نکته: از آنجایی که یک متغیر عامل در این تحلیل به کار رفته است، می‌توان آن را یک تحلیل واریانس چند متغیره یک طرفه (one-way MANOVA) نامید.

نتیجه اجرای کدها توسط دستور print‌ قابل نمایش است. خروجی به صورت یک جدول شبیه جدول تحلیل واریانس است.

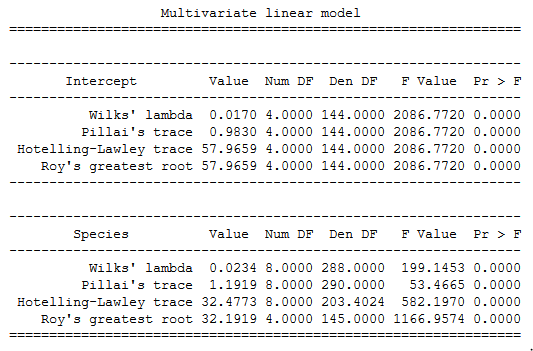
از آنجایی که مقدار هر یک از آماره آزمون مربوط به میانگین کل (Intercept) و متغیر عامل (Species) بزرگ بوده یا مقدار احتمال برایشان کوچکتر از $$0.05$$ است، آزمون یکسان بودن تاثیر نوع یا گونه زنبق روی طول و پهنای گلبرگ و کاسبرگ‌ها رد می‌شود. در نتیجه می‌توان گفت که حداقل یکی از گونه‌های گل زنبق دارای مشخصات و اندازه‌های کاملا متفاوتی با دیگران است.

جمع‌بندی و نتیجه‌گیری

در این نوشتار با مبانی اولیه و نحوه انجام محاسبات آماره آزمون تحلیل واریانس چند متغیره (MANOVA) آشنا شدیم و برای انجام تحلیل از کتابخانه statmodels در زبان برنامه‌نویسی پایتون استفاده کردیم. به منظور اجرای این تحلیل روی داده‌های واقعی از مجموعه مقادیر گل‌های زنبق (Iris) استفاده کرده و نتایج را در قالب یک جدول نمایش دادیم. در نهایت مشخص شده که گونه‌های گل روی طول و پهنای کاسبرگ و گلبرگ تاثیر گذار هستند و میانگین آن‌ها در بین گروه‌ها تغییر می‌کند.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات
• آموزش آنالیز واریانس با SPSS
• مجموعه آموزش‌های برنامه‌نویسی پایتون
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده
• توزیع نرمال و توزیع نرمال استاندارد — به زبان ساده
• متغیر فاکتور (Factor) یا متغیر عامل در R — راهنمای کاربردی

^^