تحلیل واریانس دو طرفه در پایتون — راهنمای گام به گام

تحلیل واریانس دو طرفه (two way ANOVA) معمولا برای مقایسه میانگین چند جامعه که تحت دو یا چند متغیر عامل قابل تشخیص هستند به کار می‌رود. در حقیقت این روش استنباط آماری، توسعه یافته روش تحلیل واریانس یک طرفه (one way ANOVA) است که در دیگر نوشتار فرادرس قبلا به آن پرداخته شد. در این مطلب با تحلیل واریانس دو طرفه در پایتون آشنا شده و البته مقدمات و پیش‌نیازهای مربوط به روند محاسبات و انجام چنین تحلیلی نیز ارائه می‌شود.

به منظور آشنایی بیشتر با موضوع تحلیل واریانس و شیوه تجزیه واریانس به واریانس یا تغییرات درون و بین گروهی بهتر است مطلب تحلیل واریانس (Anova) — مفاهیم و کاربردها را مطالعه کنید. البته خواندن مطلب آنالیز واریانس (ANOVA) یک و دو طرفه در R — راهنمای کاربردی نیز خالی از لطف نیست.

تحلیل واریانس دو طرفه در پایتون

یکی از تکنیک‌های مهم و پرکاربرد در آزمون فرض آماری و تحلیل داده‌ها، «تحلیل واریانس» (Analysis of Variance) است. به کمک این تکنیک سعی بر این است که اختلاف بین چند جامعه آماری، مورد بررسی قرار گرفته و در مورد تفاوت یا یکسان بودن آن‌ها رای صادر شود.  توجه به پراکندگی حول میانگین به جای بررسی و مقایسه میانگین چند جامعه از ابتکارات دانشمند شهیر و بزرگ آمار، «سِر رونالد فیشر» (Sir Ronald Fisher) است. در این روش، تغییرات کل داده‌ها، به اجزای تشکیل دهنده واریانس برحسب عوامل (Factors) تفکیک می‌شود که هر جزء بخشی از تغییرات کل را در خود جای داده است.

فیلم آموزش تجزیه و تحلیل اطلاعات با نرم افزار SAS ساس در فرادرس

کلیک کنید

در این نوشتار هر جا احتیاج به انجام محاسبات مربوط به تحلیل واریانس وجود داشته باشد، از زبان برنامه نویسی پایتون و کتابخانه‌های غنی آن استفاده خواهد شد. البته ابتدا محاسبات را بدون استفاده از کتابخانه انجام داده سپس از توابع موجود در کتابخانه‌های پایتون که بخصوص دارای توابع مربوط به تحلیل واریانس دو طرفه هستند، کمک می‌گیریم.

تحلیل واریانس دو طرفه چیست؟

در حقیقت تحلیل یا آنالیز واریانس، یک ابزار و تکنیک آماری توسعه یافته و جایگزینی برای آزمون میانگین T test برای چندین جامعه مستقل است. مشخص است که در تحلیل واریانس دو طرفه، دو متغیر عامل یا فاکتور برای تعیین جوامع به کار رفته‌اند و ترکیب سطوح این دو متغیر جامعه‌ها را مشخص می‌کند.

برای مثال فرض کنید متغیر عاملی به نام A دارای دو سطح $$a_1$$ و $$a_2$$ است. از طرفی متغیر عامل دوم به نام B نیز با سه سطح $$b_1$$، $$b_2$$‌ و $$b_3$$ وجود دارد. در نتیجه تعداد حالاتی که می‌توان جوامعی مختلفی را با این دو متغیر عامل ایجاد کرد برابر است با:

$$\large A\times B =2\times 3=6$$

در نتیجه شش حالت مختلف وجود خواهد داشت که می‌توان سطوح این دو متغیر را با یکدیگر ترکیب کرد. به همین علت گاهی تحلیل واریانس دو طرفه را با نام تحلیل فاکتوریل (Factorial) نیز می‌نامند زیرا ترکیب‌های مختلف سطوح متغیرهای عامل در تشکیل جوامع نقش دارد. البته ممکن است بعضی از گروه‌بندی‌ها واقعا وجود نداشته یا مورد علاقه ما نباشند. بنابراین این حاصلضرب سطوح این دو عامل، حداکثر تعداد گروه‌بندی یا جوامع را نشان می‌دهد.

نکته: باید توجه داشت که در صورت اضافه کردن متغیرها عامل ممکن است بهبودی در کاهش خطای مدل بوجود بیاید ولی با این کار پیچیدگی مدل زیاد شده و محاسبات زمان‌بر خواهند شد. برای مثال اگر ۵ متغیر عامل با سطوحی یکسان و برابر با ۴ داشته باشیم، تعداد بررسی‌ها و گروه‌ها ممکن برابر است با:

$$\large 4 \times 4 \times 4 \times 4 \times 4= 4^5=1024$$

که بررسی و تحلیل این تعداد جامعه یا گروه کار بسیار مشکل و پیچیده‌ای خواهد بود.

تغییرات پراکندگی ناشی از متغیر عامل A یا B را «اثرات اصلی» (Main Effect) و تغییرات حاصل از حضور هر دو متغیر بطور همزمان را «اثرات متقابل» (Interaction) می‌نامند و با $$A\times B$$ نشان می‌دهند.

نکته: گاهی به جای اصطلاح سطوح متغیر عامل از عبارت «تیمار» (Treatment) استفاده می‌شود.

فرض کنید مدلی فقط با اثرات اصلی مورد نظر باشد. در این صورت مقدار هر مشاهده که با $$x_{ijk}$$ نشان داده شده است، حول میانگن کل یا $$\mu$$ و تحت تاثیر میانگین عامل A‌ و عامل B و همچنین متغیر خطا $$\epsilon$$ تغییر خواهد کرد. در نتیجه مدلی که برای مشاهدات می‌توان در نظر گرفت مطابق با رابطه ۱ خواهد بود که تاثیر عوامل به صورت خطی و جمعی در نظر گرفته شده است.

$$\large x_{{ij}}=\mu +\alpha _{i}+\beta _{j}+\epsilon _{{ijk}}$$

رابطه ۱

اگر مدل، همراه با اثرات اصلی و اثرات متقابل باشد می‌توان آن را با اصافه کردن جمله دیگری کامل کرد.

$$\large x_{{ij}}=\mu +\alpha _{i}+\beta _{j}+\gamma _{{ij}} +\epsilon_{ijk}$$

رابطه ۲

شکل زیر نمایانگر نحوه تجزیه پراکندگی کل ($$SS_T$$) یا همان Sum of Square Total است که به پراکندگی درون گروهی ($$SS_{within}$$) و پراکندگی اثرات اصلی ($$SS_A$$, $$SS_B$$) و پراکندگی اثرات متقابل ($$SS_{A\times B}$$) تفکیک شده است.

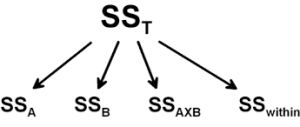
شرط‌های زیر برای چنین مدلی در نظر گرفته می‌شود:

• باقی‌مانده‌ها یا جمله‌ خطا تصادفی هستند.
• باقی‌مانده‌ها یا جمله‌ خطا مستقل از یکدیگرند.
• توزیع احتمالاتی باقی‌مانده‌ها یا جمله خطا، نرمال با میانگین صفر و واریانس ثابت $$\sigma^2$$‌ است. به این معنی که در بین جوامع فقط میانگین تغییر یافته ولی واریانس در آن‌ها ثابت و برابر است.
• پارامترها قابل شناسایی هستند. به این منظور محدودیت زیر را برای پارامترهای مدل در نظر می‌گیریم.

$$\large {\displaystyle \sum _{i}\alpha _{i}=\sum _{j}\beta _{j}=\sum _{i}\gamma _{ij}=\sum _{j}\gamma _{ij}=0}$$

از طرفی در حالتی که تحلیل به صورت متوازن (Balanced) صورت گیرد، تعداد مشاهدات در هر دسته یا گروه برابر خواهد بود. بنابراین اگر $$n_{ij}$$‌ بیانگر تعداد اعضای گروه در سطح $$i$$ام فاکتور A و سطح $$j$$ام فاکتور B باشد، خواهیم داشت.

$$\large {\displaystyle \forall i,j;\;\;n_{ij}=K}$$

ولی اگر این شرط وجود نداشته باشد به این تحلیل واریانس، تحلیل نامتوازن (Unbalance) گفته شده ولی رابطه زیر را خواهیم داشت که در آن $$n$$ بیانگر تعداد مشاهدات نمونه تصادفی از جامعه‌ها است.

$$\large {\displaystyle \forall i,j\;\sum_{i,j}n_{ij}=n},$$

نکته: اغلب برای نمایش ارتباط بین دو متغیر عامل روی متغیر وابسته که همان میانگین هر جامعه است از یک جدول توافقی استفاده می‌کنند که سطوح مختلف عامل اول در سطرها و سطوح عامل دوم نیز ستون قرار گرفته است. به همین علت گاهی تغییرات عامل A را به صورت $$SSR$$ یا Sum of Square of Rows و تغییرات عامل B را با $$SSC$$ یا Sum of Square Columns نیز نشان می‌دهند. همچنین به این شکل، پراکندگی براساس اثرات متقابل نیز با $$SSI$$ یا همان Sum of Square Interaction مشخص می‌شود.

به این ترتیب می‌توان پراکندگی‌ها برای تحلیل واریانس دو طرفه را به صورت زیر نمایش داد.  توجه داشته باشید که منظور از $$\bar{X}$$‌ همان میانگین کل حاصل از نمونه است.

جدول ۱- جملات و نحوه محاسبات برای تحلیل واریانس دو طرفه

مشابه آنچه در تحلیل واریانس یک طرفه گفته شد، جدولی برای معرفی مقادیر و نسبت‌های مربوط به انجام آزمون آماری مقایسه میانگین نیاز است. در اینجا نیز جدولی به نام جدول تحلیل واریانس دو طرفه وجود دارد که در حالت کامل (در نظر گرفتن اثرات متقابل) به صورت زیر در خواهد آمد.

مانند هر آزمون دیگر، آنالیز واریانس دو طرفه نیز احتیاج به یک آماره آزمون دارد. آماره آزمون برای  two way ANOVA دارای توزیع F است.

جدول ۲- جدول تحلیل واریانس دو طرفه به همراه اثرات متقابل

نکته: گاهی تغییرات درون گروهی با نماد $$SSW$$ را در مباحث مدل‌های خطی و رگرسیون با نام تغییرات خطا نیز مشخص می‌کنند و با نماد $$SSE$$‌ و میانگین آن را با $$MSE$$ می‌شناسند.

هر گاه مقدار $$F$$‌ مربوط به هر یک از عوامل بزرگتر از مقدار توزیع F‌ متناظر با درجه‌های آزادی باشد فرض بی‌تاثیر بودن آن عامل در تغییر میانگین رد می‌شود. در حقیقت وجود تاثیر عامل در تغییر میانگین به اثبات می‌رسد و می‌توان گفت که این عامل باعث تفکیک جامعه خواهد شد. اگر برای هر دو عامل $$A$$ و $$B$$ همچنین اثرات متقابل $$A\times B$$ این اتفاق بیافتد می‌توان گفت که میانگین تحت تاثیر هر دو عامل و به طور همزمان قرار دارد.

اگر میانگین جامعه در سطح $$i$$ام عامل $$A$$ و $$j$$ام عامل $$B$$ را به صورت $$\mu_{ij}$$‌ نشان دهیم و هدف انجام آزمون فرض آماری مبنی بر تاثیر عوامل در تغییر میانگین جوامع باشد، فرض صفر در چنین آزمونی را به صورت زیر می‌توان نوشت:

$$\large \mu_{ij}=\mu$$

که در این صورت آن را مترادف با شرایط زیر براساس رابطه ۲ باید در نظر گرفت:

$$\large \alpha_i=\beta_j=\gamma_{ij}=0$$

البته واضح است که با رد چنین فرضی به عنوان فرض صفر، مشخص می‌شود که حداقل یک عامل یا هر دو عامل همزمان یا تک تک، روی میانگین جوامع تاثیر گذار است. باید توجه داشت که فرض مقابل در چنین آزمونی همین حالت در نظر گرفته خواهد شد.

تحلیل واریانس دو طرفه در پایتون

اینک قصد داریم به کمک دستورات و کتابخانه‌های محاسبات آماری در پایتون یک تحلیل واریانس دو طرفه را اجرا کنیم. به این منظور یک مجموعه داده که دارای یک متغیر کمی (عددی با مقیاس پیوسته) را با دو متغیر کیفی که بیانگر عوامل هستند در نظر می‌گیریم.

فیلم آموزش آمار ریاضی 2 – آزمون فرض در فرادرس

کلیک کنید

مشخص است که سطوح یا هر ترکیبی از مقادیر این دو متغیر کیفی می‌تواند یک تیمار در نظر گرفته شود. ابتدا ملزومات مربوط به انجام چنین کاری را در حافظه بارگذاری می‌کنیم. دستورات مربوط به این امر در ادامه قابل مشاهده هستند.

1import pandas as pd
2import statsmodels.api as sm
3from statsmodels.formula.api import ols
4from statsmodels.stats.anova import anova_lm
5from statsmodels.graphics.factorplots import interaction_plot
6import matplotlib.pyplot as plt
7from scipy import stats

تحلیل واریانس را براساس مجموعه داده ToothGrowth.csv انجام می‌دهیم که از طریق لینک (+) قابل دریافت است. مقادیر متغیرها در این فایل با استفاده از کاما جداسازی شده‌اند.

این فایل حاوی اطلاعات ۶۰ مشاهده و سه متغیر است. متغیر اول که با نام len‌ مشخص شده است، ارتفاع دندان را برای خوکچه‌های هندی (Guinea Pigs) آزمایشگاهی نشان می‌دهد. همچنین نوع تیمار (مکمل غذایی ویتامین C) که با متغیر supp مشخص شده دارای دو سطح VC داروی ویتامین C‌ و OJ به معنی آب پرتقال است که هر دو منبع ویتامین C محسوب می‌شوند. از طرف دیگر میزان مصرف هر یک از این مکمل‌ها در سطوح 0.5، 1 و ۲ میلی‌گرم در روز به عنوان تیمار B‌ مشخص شده است.

قرار است تشخیص دهیم که نوع ویتامین C و میزان آن چه تاثیری روی میزان رشد دندان خوکچه‌های هندی مورد آزمایش دارند.

1datafile = "ToothGrowth.csv"
2data = pd.read_csv(datafile)

پس از بارگذاری این پرونده به کمک دستورات بالا یک نمودار به منظور شناسایی میانگین نمونه‌ها و تغییرات آن‌ها تحت تاثیر هر یک از تیمارها ترسیم می‌کنیم. این کار به کمک دستورات زیر صورت خواهد گرفت.

1fig = interaction_plot(data.dose, data.supp, data.len,
2             colors=['red','blue'], markers=['D','^'], ms=10)

نتیجه اجرای این دستور، نموداری است که در تصویر زیر دیده می‌شود. البته این نوع نمودار به کمک کتابخانه statmodels ترسیم شده است.

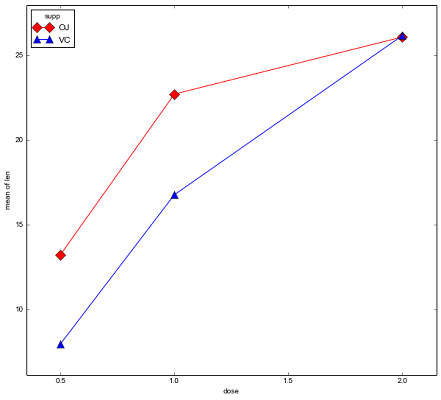
این نمودار به خوبی نشان می‌دهد که بین نوع تیمار ویتامین C اختلاف وجود دارد و دندان خوکچه‌های هندی با تیمار VC دارای میانگین ارتفاع بیشتری است. ولی این خصوصیت تا زمانی که میزان دارو کمتر یا مساوی با ۱ میلی‌گرم در روز است وجود دارد. زمانی که دوز دارو به ۲ میلی‌گرم در روز می‌رسد از لحاظ میزان اثر دو روش تیمار، تفاوتی دیده نمی‌شود. بنابراین به نظر می‌رسد که هم نوع تیمار ویتامین C‌ و هم میزان دارو در ارتفاع دندان‌های خوکچه‌های هندی تاثیر گذار است. ولی این نتایج فقط براساس نمونه تصادفی حاصل شده است. باید به کمک آزمون آماری و تکنیک تحلیل واریانس دو طرفه، دست به انجام آزمون آماری بزنیم و نتیجه را به جامعه آماری تعمیم دهیم.

در ادامه به کمک محاسبات دستی بدون استفاده از کتابخانه‌های پایتون محاسبات را انجام داده و سپس به کمک دو کتابخانه مختلف پایتون به نام‌های Statmodels و Pyvttble‌ محاسبات را انجام داده و نتایج را مقایسه می‌کنیم. البته انتظار داریم که نتایج کاملا مشابه با یکدیگر باشند.

شیوه اجرای تحلیل واریانس دو طرفه بدون کتابخانه‌های رایج

همانطور که در ابتدای متن خواندید، برای انجام تحلیل واریانس احتیاج به تجزیه واریانس براساس عوامل یا فاکتورها هستیم. فرمول‌های معرفی شده در جدول‌های قبلی، در اینجا راهنمای ما برای انجام محاسبات هستند. ابتدا درجه‌های آزادی را به کمک دستورات زیر محاسبه می‌کنیم.

1N = len(data.len)
2df_a = len(data.supp.unique()) - 1
3df_b = len(data.dose.unique()) - 1
4df_axb = df_a*df_b 
5df_w = N - (len(data.supp.unique())*len(data.dose.unique()))

سپس میانگین کل را برای متغیر len بدست می‌آوریم. در اینجا میانگین کل را با grand_mean نشان داده و در متغیری با این نام ثبت کرده‌ایم.

1grand_mean = data['len'].mean()

در ادامه نیز دستورات مربوط به محاسبه مجموع مربعات پراکندگی نسبت به میانگین برای تیمارها یا عوامل A‌ و B بدست می‌آیند. واضح است که متغیرهای مربوط به هر یک از مربعات پراکندگی متناظر با تیمار به کار رفته نام‌گذاری شده‌اند. برای مثال منظور از ssq_a مجموع مربعات پراکندگی تحت عامل A است.

مجموع مربعات پراکندگی عامل A (نوع دارو - supp)

1ssq_a = sum([(data[data.supp ==l].len.mean()-grand_mean)**2 for l in data.supp])

مجموع مربعات پراکندگی عامل B (میزان دارو - dose)

1ssq_b = sum([(data[data.dose ==l].len.mean()-grand_mean)**2 for l in data.dose])

مجموع مربعات پراکندگی کل

1ssq_t = sum((data.len - grand_mean)**2)

مجموع مربعات پراکندگی درون گروهی (جمله خطا)

1vc = data[data.supp == 'VC']
2oj = data[data.supp == 'OJ']
3vc_dose_means = [vc[vc.dose == d].len.mean() for d in vc.dose]
4oj_dose_means = [oj[oj.dose == d].len.mean() for d in oj.dose]
5ssq_w = sum((oj.len - oj_dose_means)**2) +sum((vc.len - vc_dose_means)**2)

مجموع مربعات پراکندگی اثرات متقابل

1ssq_axb = ssq_t-ssq_a-ssq_b-ssq_w

به منظور محاسبه مقدار $$F$$ که آماره آزمون مربوط به تحلیل واریانس محسوب می‌شود، احتیاج به میانگین مربعات پراکندگی‌ها یا همان MS‌ داریم. برای این کار کافی است هر یک از مقادیر حاصل از مراحل قبل را به درجه آزادی مربوطه تقسیم کنیم.

میانگین مربعات پراکندگی عامل A

1ms_a = ssq_a/df_a

میانگین مربعات پراکندگی عامل B

1ms_b = ssq_b/df_b

میانگین مربعات پراکندگی اثرات متقابل عامل‌های A و B

1ms_axb = ssq_axb/df_axb

میانگین مربعات پراکندگی درون گروهی

1ms_w = ssq_w/df_w

بر همین اساس نیز مقادیر $$F$$‌ مربوط به هر عامل و اثرات متقابل را بدست می‌آوریم.

1f_a = ms_a/ms_w
2f_b = ms_b/ms_w
3f_axb = ms_axb/ms_w

به منظور تشخیص اینکه آیا فرض صفر رد می‌شود یا خیر، باید محاسبات مربوط به مقدار احتمال (p-Value) را نیز انجام دهیم. این محاسبات به کمک کدهای زیر صورت گرفته است.

1p_a = stats.f.sf(f_a, df_a, df_w)
2p_b = stats.f.sf(f_b, df_b, df_w)
3p_axb = stats.f.sf(f_axb, df_axb, df_w)

حال که نتایج در متغیرهای مورد نظر ثبت و ذخیره شده‌اند، بهتر است قالبی شبیه جدول تحلیل واریانس دو طرفه برایشان مطابق با جدول ۲ ایجاد کنیم. دستورات زیر به این منظور تهیه شده‌اند.

1results = {'sum_sq':[ssq_a, ssq_b, ssq_axb, ssq_w],
2           'df':[df_a, df_b, df_axb, df_w],
3           'F':[f_a, f_b, f_axb, 'NaN'],
4            'PR(>F)':[p_a, p_b, p_axb, 'NaN']}
5columns=['sum_sq', 'df', 'F', 'PR(>F)']
6
7aov_table1 = pd.DataFrame(results, columns=columns,
8                          index=['supp', 'dose', 
9                          'supp:dose', 'Residual'])

البته اندازه اثر (Effect size) $$\eta$$ نیز بهتر است گزارش شود. دستورات زیر به منظور محاسبه مربع اتا ($$\eta^2$$) و امگا ($$\omega^2$$) تهیه شده است. در انتهای کد نیز جدول تحلیل واریانس ترسیم می‌شود.

1def eta_squared(aov):
2    aov['eta_sq'] = 'NaN'
3    aov['eta_sq'] = aov[:-1]['sum_sq']/sum(aov['sum_sq'])
4    return aov
5
6def omega_squared(aov):
7    mse = aov['sum_sq'][-1]/aov['df'][-1]
8    aov['omega_sq'] = 'NaN'
9    aov['omega_sq'] = (aov[:-1]['sum_sq']-(aov[:-1]['df']*mse))/(sum(aov['sum_sq'])+mse)
10    return aov
11
12
13eta_squared(aov_table1)
14omega_squared(aov_table1)
15print(aov_table1)

برای محاسبه اندازه اثر مثلا برای عامل A، فرمول‌ها و شیوه بدست آوردن هر یک از شاخص‌های $$\eta$$ و $$\omega$$ مطابق با را فرمول‌ها زیر است.

$$\large \eta^2_A=\dfrac{SSA}{SST}$$

$$\large \omega^2_A=\dfrac{SSA-df_A\times MSW}{SST+MSW}$$

خروجی جدول تحلیل واریانس

واضح است که با توجه به کوچک بودن همه مقادیر $$PR(>F)$$‌ فرض صفر که به معنی بی‌تاثیر بودن تیمارها است رد می‌شود. حتی تاثیر متقابل تیمارها نیز در سطح آزمون 0.05 رد می‌شود.

تحلیل واریانس دو طرفه به کمک کتابخانه statmodels

به منظور انجام تحلیل واریانس دو طرفه در پایتون می‌توان از کتابخانه statmodels به همراه توابع آن استفاده کرد. به این ترتیب انجام محاسبات بسیار ساده‌تر شده و با کدهای کمتری می‌توان به نتایج مورد نظر رسید.

فیلم آموزش برنامه نویسی پایتون Python – مقدماتی در فرادرس

کلیک کنید

کدی که در ادامه مشاهده می‌کنید براساس کتابخانه statmodels نوشته شده که بسیار شبیه به قالبی است که در زبان برنامه‌نویسی R‌ برای انجام تحلیل واریانس وجود دارد.

1formula = 'len ~ C(supp) + C(dose) + C(supp):C(dose)'
2model = ols(formula, data).fit()
3aov_table = anova_lm(model, typ=2)

از آنجایی که دستور anova_lm امکان محاسبه اندازه اثر را ندارد، کدهای زیر را براساس توابع معرفی شده در بخش قبل را به کار گرفته و در انتها نیز جدولی خروجی را ایجاد می‌کنیم.

1eta_squared(aov_table)
2omega_squared(aov_table)
3print(aov_table.round(4))

نتایج حاصل درست به مانند جدول آنالیز واریانس قبلی خواهد بود.

یکی از شرایط مربوط به تحلیل واریانس، نرمال بودن باقی‌مانده‌ها یا همان مشاهدات است. کد زیر به منظور رسم نمودار چندک در مقابل چندک (Q-Q plot) نوشته شده است. اگر توزیع مربوط به خطاها یا باقی‌مانده‌ها همان توزیع نرمال باشد، شکل این نمودار باید به یک خط راست نزدیک باشد. در حقیقت این نمودار نشان می‌دهد که توزیع تجربی باقی‌مانده چقدر به توزیع نرمال نزدیک است.

1res = model.resid 
2fig = sm.qqplot(res, line='s')
3plt.show()

حاصل اجرای این دستورات نموداری است که نشانگر وجود شرط نرمال بودن برای مشاهدات است. البته در مقادیر ابتدایی و انتهایی کمی از توزیع نرمال منحرف می‌شوند که زیاد مسئله‌ای برای مدل و فرضیات ما ایجاد نخواهد کرد. ولی به هر حال به نظر می‌رسد که توزیع باقی‌مانده‌ها کمی دم-سنگین‌تر از توزیع نرمال هستند یا چولگی وجود دارد. البته برای نمایش تصادفی بودن باقی‌مانده نیز می‌توان از طریق رسم نمودارها نیز عمل کرد که در اینجا به علت مفصل بودن این مبحث به آن نپرداخته‌ایم.

تحلیل واریانس دو طرفه به کمک کتابخانه pyvttbl

هر چند دستورات مربوط به کتابخانه pyvttble کمی قدیمی هستند ولی قدرت بالایی دارند. در ادامه کدهای مربوط به تحلیل واریانس دو طرفه از طریق به کارگیری این کتابخانه قابل مشاهده است.

1from pyvttbl import DataFrame
2df=DataFrame()
3df.read_tbl(datafile)
4df['id'] = xrange(len(df['len']))
5
6print(df.anova('len', sub='id', bfactors=['supp', 'dose']))

نکته: از آنجایی که این کتابخانه قدیمی است، لازم است که کتابخانه Numpy با نسخه حداکثر 1.1 را نصب داشته باشید. در غیر اینصورت ممکن است با پیغام خطای unsupported operand type(s) for +: ‘float’ and ‘NoneType’‎ مواجه شوید. پس بهتر است کتابخانه Numpy را به نسخه‌های قدیمی برگردانید.

خروجی این کار مطابق با جدول زیر خواهد بود.

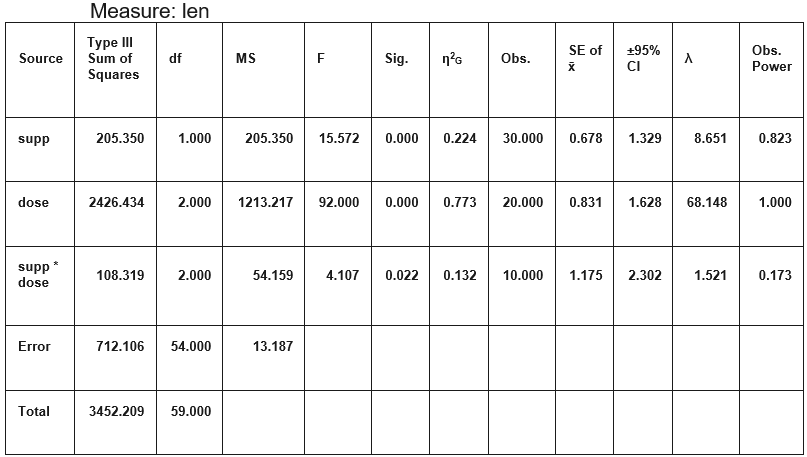
تحلیل واریانس دو طرفه به کمک کتابخانه pingouin

با توجه به جایگزینی کتابخانه pingouin با کتابخانه pyvttbl در پایتون بهتر است روش اجرای تحلیل واریانس دو طرفه را با استفاده از توابع این کتابخانه را هم فرا بگیریم. در ادامه کدهایی مربوطه آورده شده‌اند.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

ابتدا مجموعه داده بارگذاری شده، و بعضی از مقادیر آن نمایش داده می‌شود.

1import pandas as pd
2import pingouin as pg
3
4data = 'https://vincentarelbundock.github.io/Rdatasets/csv/datasets/ToothGrowth.csv'
5
6df = pd.read_csv(data, index_col=0)
7df.head()

توجه داشته باشید که داده‌ها از طریق اینترنت و از یک سایت دریافت می‌شود بنابراین هنگام اجرای برنامه باید به اینترنت متصل باشید. به این ترتیب خروجی به صورت زیر خواهد بود.

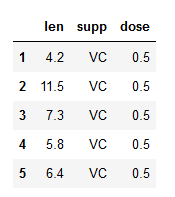
در انتها نیز دستورات و خروجی مربوطه را مشاهده می‌کنید. کاملا مشخص است که این دستورات واضح‌تر و خواناتر از دستورات قبلی برای انجام تحلیل واریانس دو طرفه هستند.

1aov = pg.anova(dv='len', between=['supp', 'dose'], data=df,
2             detailed=True)
3
4print(aov)

استنباط در مورد فرض صفر و نتایج حاصل از مقادیر p-unc‌ که همان مقدار احتمال (p-value) است با جدول‌های قبلی کاملا مطابقت دارد.

جمع‌بندی و بررسی نتایج

در این نوشتار به بررسی تحلیل واریانس دو طرفه و مقایسه آن با تحلیل واریانس یک طرفه پرداختیم. همچنین نحوه انجام محاسبات مربوط به را هم با کتابخانه‌ها و هم بدون استفاده از کتابخانه‌های پایتون مرور کردیم. با توجه به خروجی‌های تولید شده تاثیر میزان دارو و نوع دارو در ارتفاع دندان خوکچه‌های هندی مورد بررسی قرار گرفت و مشخص شد که هر دو عامل روی متوسط ارتفاع دندان‌ها تاثیر گذار هستند.

اگر این مطلب برای شما مفید بوده است و علاقه‌مند به یادگیری بیشتر در این زمینه هستید، آموزش‌ها و نوشتارهای زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های برنامه‌نویسی پایتون Python
• آموزش تکمیلی برنامه‌نویسی R و نرم‌افزار RStudio
• آنالیز واریانس (ANOVA) یک و دو طرفه در R — راهنمای کاربردی
• تحلیل واریانس (Anova) — مفاهیم و کاربردها
• تحلیل واریانس یک طرفه در پایتون --- راهنمای گام به گام

^^