تجزیه کسر — به زبان ساده

تجزیه کسر یکی از روش‌های مرسوم در ریاضیات است که به کمک آن می‌توان عملیات مختلف مانند مشتق‌گیری و انتگرال‌گیری را بسیار ساده‌تر انجام داد. ایده اصلی این موضوع یعنی تجزیه یک کسر به چند کسر ساده، تجزیه یک چند جمله‌ای به حاصل ضرب چند عبارت ساده‌تر است. همچنین توجه کنید که تجزیه چند جمله‌ای‌ها را با روش‌های گوناگونی مانند نوشتن اتحادهای مختلف می‌توان بیان کرد.

این مطلب ابتدا به صورت دقیق تعریف درستی از کسر جزئی را ارائه می‌کند. در ادامه تجزیه یک کسر به چند کسر جزئی به کمک مثال مورد مطالعه قرار می‌گیرد و نکات مختلف مربوط به این مفهوم به همراه چند مثال شرح داده می‌شود. در انتهای مطلب نیز یک مثال جامع که نکات ذکر شده در مطلب را در بر گرفته، از صفر تا صد مورد بررسی قرار می‌گیرد. همچنین شیوه انتگرال‌گیری به کمک تجزیه کسر در مطلب «انتگرال گیری به روش کسرهای جزئی» به صورت دقیق مورد بررسی قرار گرفته است.

کسر جزئی چیست؟

به صورت خلاصه می‌توان بیان کرد که تجزیه کسر، روشی است که به کمک آن می‌توان یک کسر را به صورت مجموع دو کسر ساده بیان کرد.

این دو کسر ساده را کسر جزئی می‌نامند. برای شروع این مطلب، جمع دو کسر از طریق هم مخرج کردن کسرها را به یاد بیاورید. این موضوع در رابطه زیر نشان داده شده است.

شیوه محاسبه رابطه بالا و هم مخرج کردن کسر‌ها این گونه است که صورت و مخرج کسر اول را در مخرج کسر دوم و صورت و مخرج کسر دوم را در مخرج کسر اول ضرب می‌کنیم.

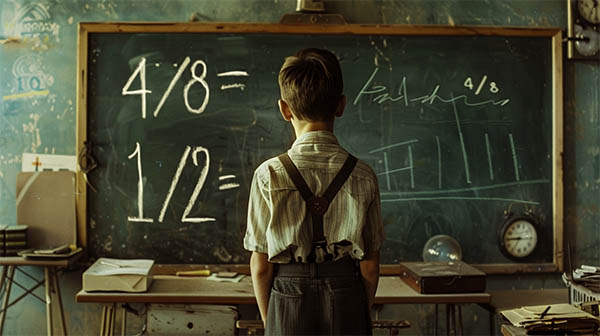
بنابراین مخرج دو کسر یکسان می‌شوند. حال، صورت‌ها را می‌توانیم با یکدیگر جمع کنیم. این موضوع در رابطه زیر نشان داده شده است.

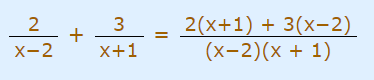
با ساده کردن طرف راست عبارت بالا، فرم نهایی جمع دو کسر نشان داده شده را می‌توان به شکل زیر نوشت.

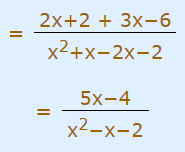
در این مطلب، تجزیه کسر مورد مطالعه قرار می‌گیرد. مراحل مختلف تجزیه یک کسر دقیقا عکس روندی است که در هم مخرج کردن و جمع کسرها طی شد. بنابراین همانطور که در رابطه زیر نشان داده شده، هدف ما این است که برای مثال یک کسر با رابطه $${5x -4} \over {x^2 - x -2}$$ به صورت جمع دو کسر جزئی نوشته شود که این روند را تجزیه کسر می‌نامند.

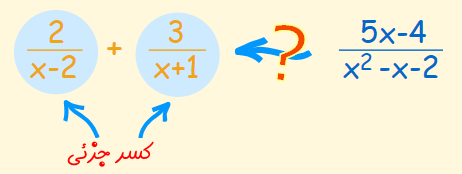
بنابراین همانطور که اشاره شد، موضوعی که در این مطلب به دنبال آن هستیم این است که یک کسر را چگونه می‌توان به صورت حاصل جمع دو کسر دیگر نوشت و هدف از این کار این است که شیوه نمایش یک کسر پیچیده را تغییر دهیم و آن را به صورت مجموع دو یا چند کسر ساده‌تر بیان کنیم. به این کسرهای ساده، کسر جزئی می‌گویند. نکته دیگری که باید به آن اشاره کرد این است که بیان کسرها به شیوه ساده‌تر (مجموع کسرهای جزئی) یکی از روش‌های بسیار پرکاربرد در محاسبه انتگرال‌ها است.

تجزیه کسر به کسرهای جزئی

در این قسمت به صورت دقیق، روش تجزیه یک کسر به مجموع دو یا چند کسر جزئی بیان می‌شود. این روش را می‌توان با استفاده از چهار گام کلی بیان کرد. این گام‌ها در ادامه به صورت دقیق مورد بررسی قرار گرفته است.

گام اول در این روش این است که مخرج کسر اولیه که یک چند جمله‌ای است را به صورت حاصل ضرب دو یا چند، چند جمله‌ای دیگر بنویسیم. برای این کار می‌توان از اتحاد‌های مختلف استفاده کرد و یا از عبارت خاصی فاکتورگیری کرد. این گام را برای مثال نشان داده شده، می‌توان به شکل زیر نمایش داد.

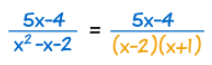
گام دوم در تجزیه کسر این است که برای هرکدام از عبارات فاکتورگیری شده در مخرج، یک کسر جزئی بنویسیم. در این مثال مخرج کسر جزئی اول، عبارتی برابر با x-2 است و مخرج کسر جزئی دوم برابر با x+1 در نظر گرفته می‌شود. این گام برای مثال ابتدای مطلب، به صورت زیر قابل بیان است.

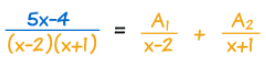
در گام سوم از مراحل تجزیه کسر، باید دو کسر با صورت مجهول که در سمت راست رابطه بالا قرار دارند را با یکدیگر هم مخرج کنیم.

بنابراین مخرج دو کسر سمت راست و چپ با یکدیگر برابر می‌شود و تنها نیاز است که صورت این دو کسر را با یکدیگر برابر قرار می‌دهیم. این گام برای مثال ابتدای این مطلب به شکل زیر نشان داده شده است.

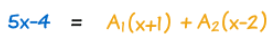
گام چهارم در تجزیه کسر این است که دو مجهول یعنی A₁ و A₂ را محاسبه کنیم. برای اجرای این گام، راحت‌ترین کار این است که مقدار x را طوری قرار دهیم که یکبار x+1 و بار دیگر x-2 برابر با صفر شود. بنابراین ابتدا x را برابر با 1- قرار می‌دهیم که ریشه عبارت x+1 است و عبارت فوق را به شکل زیر بازنویسی می‌کنیم.

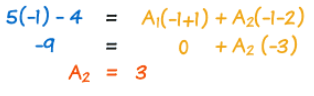
بنابراین طبق رابطه بالا، مقدار A₂ برابر با ۳ است. حال x را برابر با 2 قرار می‌دهیم. این مقدار ریشه عبارت x-2 است یعنی رابطه x-2 را برابر با صفر قرار می‌دهد. بر این اساس با جایگذاری x=2 داریم:

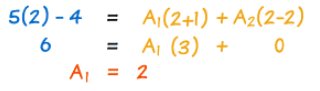
با توضیحاتی که در بالا داده شد، دو ضریب مجهول A₁ و A₂ محاسبه شد و می‌توان فرم تجزیه شده کسر را به شکل زیر نمایش داد.

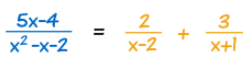
مثالی که در این بخش به صورت گام به گام بررسی شد، به راحتی توانست مفهوم تجزیه کسرها را بیان کند. اما توجه کنید که این کار یعنی تجزیه کسرها به صورت کسرهای جزئی در برخی از حالات می‌تواند بسیار پیچیده باشد. در ادامه به صورت ریز و جزئی به بیان نکات مختلف مربوط به هریک از گام‌های حل در مبحث تجزیه کسر پرداخته می‌شود.

انتخاب کسر مناسب در تجزیه کسرها

توجه کنید که روند توضیح داده شده، تنها برای کسرهایی کاربرد دارد که درجه صورت آن‌ها از درجه مخرجشان کمتر است. درجه یک چند جمله‌ای در مطلب «چندجمله‌ای‌ها – به زبان ساده» به خوبی مورد بررسی قرار گرفته است.

توجه کنید که درجه یک چند جلمه‌ای برابر بزرگترین توان موجود در چندجمله‌ای است. بنابراین همانطور که اشاره شد، در مبحث تجزیه یک کسر باید دقت کنیم که درجه صورت از مخرج کمتر باشد. این موضوع در دو مثال زیر به خوبی مورد بررسی قرار گرفته است.

طبق توضیحات بالا، حالت مناسب، حالتی است که درجه صورت از مخرج کمتر باشد. این حالت در رابطه زیر نشان داده شده است.

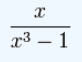
در رابطه بالا، درجه صورت برابر با 1 و درجه مخرج برابر با 3 است. بنابراین درجه صورت از درجه مخرج کمتر است و این کسر یک کسر مناسب در روش ذکر شده برای تجزیه کسرها به حساب می‌آید. همچنین اشاره شد که کسر نامناسب در تجزیه کسر، کسری است که درجه صورت از درجه مخرج بیشتر باشد. مثالی از این نوع کسرها در رابطه زیر نشان داده شده است.

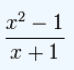
در این مثال، درجه صورت برابر با 2 و درجه مخرج برابر با 1 است. بنابراین کسر فوق برای تجزیه کسرها مناسب نیست.

فاکتورگیری از مخرج

همانطور که در بخش قبل اشاره شد، اولین گام در تجزیه یک کسر این است که مخرج آن کسر را به صورت حاصل ضرب دو یا چند، چند جمله‌ای بنویسیم که می توان این کار را با استفاده از فاکتورگیری انجام داد.

توجه کنید که کاملا به شما بستگی دارد که چگونه از چند جمله‌ای موجود در مخرج فاکتورگیری کنید ولی حتما دقت کنید که چند جمله‌ای حاضر در مخرج به عواملی شامل اعداد مختلط تجزیه نشود. بنابراین نیاز هست که گاهی چند جمله‌ای با درجه دو را دیگر تجزیه نکنیم تا عوامل مختلط ایجاد نشوند.

برای مثال فرض کنید که مخرج یک کسر برای تجزیه کسر شامل عبارت (X²-4)(X²+4) است. در این حالت عبارت اول یعنی (X²-4) را می‌توان به شکل زیر تجزیه کرد.

$$x^2 -4 = (x-2)(x+2)$$

اما عبارت دوم یعنی (X²+4) را دیگر نمی‌توان به عواملی تجزیه کرد زیرا ریشه این عبارت شامل اعداد مختلط می‌شود. بنابراین در مجموع عبارت (X²-4)(X²+4) به صورت زیر فاکتورگیری می‌شود.

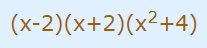
بنابراین به صورت کلی می‌توان بیان کرد که عوامل فاکتورگیری شده در مخرج کسر شامل دو بخش است. بخش اول شامل فاکتورهای درجه یک و خطی است و بخش دوم فاکتورهای درجه دو را تشکیل می‌دهند که نمی‌توان آن‌ها را به عوامل غیر مختلط دیگر تجزیه کرد.

نکته مهم دیگری که باید به آن اشاره کرد این است که وقتی شما یک فاکتور درجه دو (معادله درجه دو) در مخرج تولید کرده‌اید. کسر تجزیه شده نهایی حتما باید شامل کسر جزئی به شکل زیر باشد.

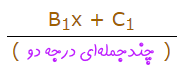
حضور فاکتورهای توانی در مخرج

برخی از اوقات در گام اول تجزیه کسر و هنگام فاکتورگیری از مخرج آن کسر به عبارتی با توان مشخص مانند $$(x-2)^3$$ می‌رسیم.

در این حالت باید برای هرکدام از توان‌ها (از یک تا توان معلوم) یک کسر جزئی نوشته شود. برای فهم دقیق این موضوع به مثال زیر توجه کنید.

مثال 1

کسرهای جزئی لازم برای تجزیه کسر زیر را بنویسید.

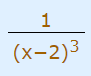
همانطور که بیان شد زمانی که در مخرج کسر، یک چند جمله‌ای با توان مشخص حضور دارد، باید به اندازه توان چند جمله‌ای یعنی از یک تا توان معلوم (در اینجا از یک تا سه)، کسر جزئی بنویسیم. این موضوع در رابطه زیر نشان داده شده است.

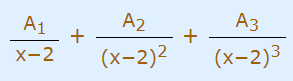
مفهومی که در این بخش مطالعه شد را می‌توان برای رابطه درجه دو در مخرج کسر که توان مشخصی دارد نیز به کار برد. برای فهم دقیق‌تر این موضوع به مثال زیر توجه کنید.

مثال 2

کسر زیر که مخرج آن یک چند جمله‌ای درجه دو است را در نظر بگیرید و کسرهای جزئی لازم برای تجزیه این کسر را بنویسید.

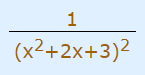
در اینجا با توجه به توان 2 در عبارت مخرج، تجزیه این کسر نیاز به دو کسر جزئی دارد و این دو کسر جزئی را می‌توان به شکل زیر بیان کرد.

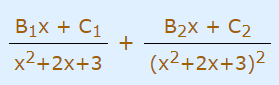
توجه کنید که با توجه به درجه دو بودن عبارت مخرج، صورت این دو کسر جزئی باید به صورت یک عبارت درجه یک در نظر گرفته شود.

توجه کنید که در بسیاری از حالات، پس از نوشتن کسرهای جزئی و برای محاسبه ضرایب، نیاز به حل یک دستگاه چند معادله چند مجهول (با توجه به تعداد مجهولات مسئله) داریم. در ادامه و به کمک یک مثال، روابط و نکاتی که در این مطلب ذکر شد را از صفر تا صد مورد مطالعه قرار می‌دهیم.

مثال جامع برای تجزیه کسر

در این قسمت یک مثال جامع بیان شده که حل آن شامل نکات اساسی است و نیاز به صرف زمان زیاد و انجام محاسبات خاصی نیز دارد.

بنابراین کسر زیر را در نظر بگیرید و آن را به کسر‌های جزئی تجزیه کنید.

توجه کنید که عبارت $$(x+3)^2$$ شامل توان دو است. بنابراین برای بیان آن نیاز به دو کسر جزئی با صورت A₁ و A₂ است. نکته دیگر این است که عبارت بعدی موجود در مخرج یعنی $$(x^2+3)$$ یک عبارت درجه دو است و صورت کسر جزئی آن را باید به شکل Bx +C بیان کرد. بنابراین در مجموع، کسر بالا را می‌توان به شکل زیر تجزیه کرد.

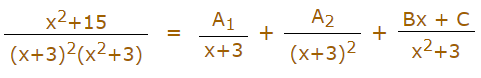
حال، هر دو طرف رابطه بالا را در عبارت $$(x+3)^2(x^2+3)$$ ضرب می‌کنیم و در نهایت رابطه بالا به فرم زیر در می‌آید.

برای محاسبه ضرایب موجود، یعنی B ،A₂ ،A₁ و C، ابتدا مقدار x = -3، را در رابطه بالا قرار می‌دهیم. بنابراین داریم:

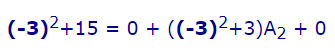
رابطه بالا را می‌توان برای یافتن ضریب A₂ به شکل ساده شده زیر نوشت.

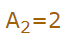
بنابراین A₂ را برابر با 2 قرار می‌دهیم و رابطه بین ضرایب به شکل ساده شده زیر در می‌آید.

حال، روابط را به فرم بسط داده شده می‌نویسیم.

رابطه بالا را به فرم ساده شده زیر بیان می‌کنیم و در آن، ضریب توان‌های مختلف x را با یکدیگر جمع می‌کنیم.

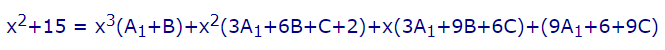
در ادامه ضریب توان‌های مختلف x در دو طرف رابطه را با یکدیگر برابر قرار می‌دهیم. بنابراین داریم:

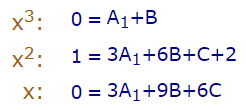
اعداد ثابت در دو طرف رابطه را نیز با یکدیگر برابر قرار می‌دهیم که رابطه بین آن‌ها به شکل زیر خواهد بود.

چهار رابطه بالا را می‌توان به فرم ساده و مرتب شده زیر بیان کرد.

همانطور که مشاهده می‌شود سه مجهول و چهار معادله داریم. شما می‌توانید به روش‌های مختلف این سه مجهول را پیدا کنید. در ادامه یکی از روش‌های خاص برای حل دستگاه معادلات مورد بررسی قرار می‌گیرد. بنابراین در ابتدا معادله چهارم را از معادله دوم تفریق می‌کنیم. در نتیجه داریم:

حال رابطه اول را دو بار از رابطه دوم کم می‌کنیم.

بنابراین از رابطه دوم در مجموعه معادلات بالا می‌توان نتیجه گرفت که مقدار B برابر با $$-(1/2)$$ است. سپس با قرار دادن مقدار B در رابطه اول، A_۱ محاسبه می‌شود که مقدار آن برابر با $$+(1/2)$$ است. همچنین با قرار دادن مقدار A₁ در رابطه چهارم، مقدار C برابر با $$+(1/2)$$ به دست می‌آید. بنابراین ضرایب مجهول در این مسئله محاسبه شدند و به صورت خلاصه می‌توان آن‌ها را به شکل زیر بیان کرد.

با استفاده از ضرایب بالا می‌توان نتیجه گرفت که فرم نهایی تجزیه شده کسر صورت سوال به شکل زیر نشان داده می‌شود.

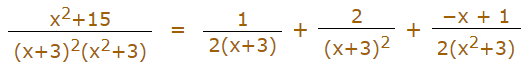
خلاصه مطلب

به صورت خلاصه می‌توان بیان کرد که برای تجزیه یک کسر به صورت کسرهای جزئی، ابتدا باید کسر مناسب را محاسبه کرد. کسر مناسب برای روابط این مطلب، کسری است که درجه صورت آن کمتر از درجه مخرج آن باشد.

گام دوم در مسیر تجزیه کسر این است که مخرج کسر اولیه را به صورت حاصل ضرب عبارات درجه اول یا عبارات غیر قابل تفکیک درجه دو بنویسیم. برای این کار می‌توان از مطلب «اتحاد و تجزیه در ریاضی — به زبان ساده» استفاده کرد.

گام سوم نیز این است که برای هرکدام از فاکتورهای نشان داده شده در گام دوم، یک یا چند کسر جزئی مناسب بیان کنیم.

گام چهارم برای تجزیه کسر این است که طرفین رابطه به دست آمده در گام سوم را در مخرج کسر اولیه ضرب و معادله نهایی را به فرم مرتب و ساده شده بیان کنیم. بنابراین یک دستگاه معادلات شامل ضرایب مجهول به وجود می‌آید.

در ادامه و در گام پنجم دستگاه معادلات به دست آمده در گام چهارم را حل و ضرایب مجهول را محاسبه می‌کنیم و در نهایت در گام ششم، کسر ابتدایی را به صورت تجزیه شده بر حسب کسرهای جزئی می‌نویسیم.