بادامک – از صفر تا صد

بادامک، وسیله‌ای مکانیکی است که معمولاً برای تبدیل حرکت چرخشی به حرکت خطی مورد استفاده قرار می‌گیرد. حرکت خطی، به صورت نوسانی و رفت و برگشتی خواهد بود. بادامک (Cam) در هنگام چرخش، با میله‌ای ارتباط دارد که «پیرو» (Follower) نامیده می‌شوند. به طور کلی، هنگامی که دو عضو، از طریق تماس در سطوح مختلف، به یکدیگر متصل باشند، مفصل بادامکی تشکیل می‌شود. در این حالت، عضو ورودی که معمولاً شکل نامنظمی دارد، بادامک و عضو خروجی، پیرو نامیده می‌شود.

انتقال حرکت از بادامک به پیرو، به صورت تماس مستقیم است. در زوج بادامک-پیرو، معمولاً بادامک می‌چرخد و پیرو، حرکت خطی دارد. حرکت‌های پیچیده‌ای که در حالت عادی، انجام آن دشوار است، به کمک بادامک بسیار راحت خواهد بود. از بادامک‌ها به طور گسترده در موتورهای احتراق داخلی، ماشین‌های چاپ، صنایع نساجی و غیره استفاده می‌شود. در برخی از مکانیزم‌های بادامک، علاوه بر بادامک و پیرو، به یک قاب هم نیاز است تا پیرو در مسیر هدایت شده حرکت کند. شکل زیر، نمونه ساده‌ای از تماس بین بادامک و پیرو را نشان می‌دهد.

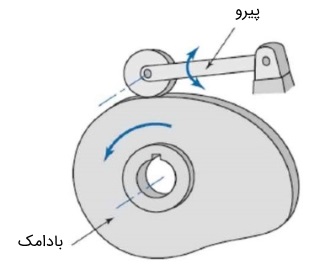
انواع بادامک

بادامک‌ها را معمولاً به سه دسته اصلی تقسیم می‌کنند. بادامک انتقالی (Wedge or Flat Cam) که در شکل زیر نشان داده شده است، ظاهری به شکل گُوِه (Wedge) دارد. این بادامک، به صورت انتقالی حرکت می‌کند.

فیلم آموزش نرم افزار Adams Machinery برای مدلسازی سیستم های انتقال قدرت در فرادرس

کلیک کنید

در این وضعیت، پیرو حرکت انتقالی یا رفت و برگشتی خواهد داشت.

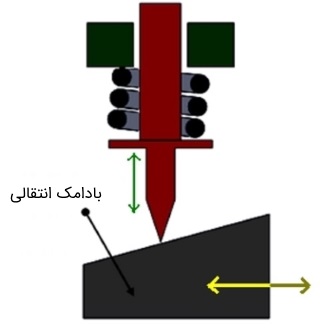
نوع دیگر بادامک را در شکل زیر می‌بینید. به این بادامک، دیسکی گفته می‌شود. بادامک دیسکی (Plate, Radial or Disk Cam)، حرکت چرخشی دارد و پیرو در صفحه‌ای عمود به محور چرخش بادامک، حرکت رفت و برگشتی انجام می‌دهد. این بادامک، که به نام‌های شعاعی یا صفحه‌ای هم شناخته می‌شود، بسیار محبوب است. زیرا هم ساده است و هم فضای کمی را اشغال می‌کند. به علت متداول بودن این نوع بادامک، محاسبات ریاضی در این مقاله، براساس همین مدل ارائه خواهد شد.

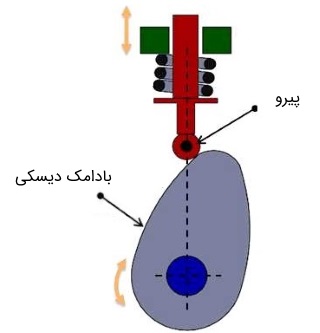
دسته سوم، بادامک‌های استوانه‌ای (Cylindrical, Drum or Barrel Cam) هستند. عملکرد این نوع بادامک‌ها در تصویر متحرک زیر نشان داده شده است. همان‌طور که مشاهده می‌کنید، شیاری روی محیط بادامک (استوانه) ایجاد شده و پیرو فقط می‌تواند روی این شیار حرکت کند. در این مدل، حرکت پیرو به صورت نوسانی یا رفت و برگشتی خواهد بود. کاربرد اصلی این نوع بادامک، تبدیل حرکت چرخشی به حرکت خطی در راستایی موازی با محور چرخش است. در برخی طراحی‌ها، بیش از یک شیار روی سطح استوانه ایجاد می‌شود. درنتیجه، بادامک می‌تواند بیش از یک پیرو را به حرکت دربیاورد.

نمودارهای جابجایی

نموداری که جابجایی پیرو را به عنوان تابعی از زمان رسم کرده باشد، نمودار جابجایی نامیده می‌شود. نمونه‌ای از این نمودار را در شکل زیر می‌بینید. محور افقی، درجه چرخش بادامک را نشان می‌دهد. در این نمودار، یک دور چرخش کامل را مشاهده می‌کنید. از آنجایی که سرعت چرخش بادامک (برحسب دور در دقیقه) ثابت است، بازه‌های تقسیم شده روی محور طولی، می‌توانند معیاری از زمان سپری شده را نیز ارائه کنند. محور عمودی، نشان دهنده جابجایی پیرو است. نمودار جابجایی، شکل بادامک را تعریف می‌کند. در تحلیل یک بادامک و یا برای طراحی یک نمونه از آن، این نمودار اهمیت فوق‌العاده‌ای دارد.

از آنجایی که این نمودار، در حقیقت، یک نمودار جابجایی برحسب زمان به شمار می‌آید، با یک و دوبار مشتق‌گیری از آن می‌توان به ترتیب، نمودارهای سرعت و شتاب برحسب زمان را نتیجه گرفت. مشتق شتاب برحسب زمان را جِرک ($$\large Jerk$$) می‌نامیم و آن را به عنوان پالس یا آهنگ تغییر شتاب تعریف می‌کنیم. شتاب پیرو در بادامک‌هایی که با سرعت زیاد کار می‌کنند، اهمیت بالایی دارد. زیرا شتاب تأثیر مستقیمی روی نیروهای اینرسی دارد و در نهایت منجر به ارتعاشات، نویز، تنش و سایش می‌شود. جرک، معیاری از آهنگ تغییر نیروی اینرسی فراهم می‌کند و در نهایت، شاخصی از ضربه در بارگذاری به حساب می‌آید. تجربه نشان داده است که بی‌نهایت بودن مقدار جرک، منجر به بروز ارتعاش در پیرو شده و روی عمر بادامک تأثیر می‌گذارد. در ادامه، انواع حرکت پیرو را بررسی می‌کنیم.

حرکت پیرو با شتاب ثابت

جابجایی جسمی که با شتاب ثابت حرکت می‌کند، با کمک رابطه $$\large s = \frac {1} {2} A t^2$$ به دست می‌آید. در این رابطه، $$\large t$$ زمان حرکت و $$\large A$$ هم شتاب است. نمودار این معادله یک سهمی است. از آنجایی که شتاب ثابت است، جابجایی $$\large s$$ با مقدار $$\large t^2$$ متناسب خواهد بود. همان‌طور که در شکل زیر مشاهده می‌کنید، شتاب در بخشی از مسیر، مثبت، در بخشی دیگر، منفی و در بخشی هم صفر است.

فیلم آموزش سینماتیک و دینامیک ماشین ها در فرادرس

کلیک کنید

در تحلیل حرکت بادامک، بهتر است جابجایی، سرعت و شتاب پیرو را به جای زمان، برحسب زاویه چرخش بادامک $$\large \theta$$ بیان کنیم. نمودار جابجایی زیر را در نظر بگیرید. منحنی $$\large AB$$ نشان دهنده بالا رفتن پیرو با شتاب ثابت است. در منحنی $$\large BC$$ هم پیرو با شتاب منفی بالا می‌رود. کل جابجایی پیرو با $$\large h$$ نشان داده شده است. در این فاصله، بادامک به اندازه $$\large \beta$$ درجه چرخیده است. با توجه به رابطه بین زمان و سرعت زاویه‌ای که به صورت $$\large \theta = \omega \times t$$ تعریف می‌شود، رابطه جابجایی را برای بخشی از نمودار که بین $$\large A$$ و $$\large B$$ قرار دارد، به صورت زیر می‌توان نوشت.

$$\large s = \frac {1} {2} A (\frac { \theta}{ \omega})^2$$

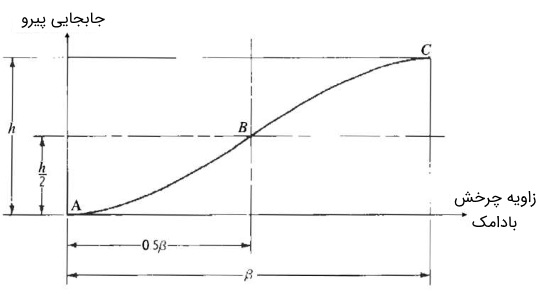
با توجه به شکل، هنگامی که جابجایی $$\large s = \frac {h} {2}$$ باشد، زاویه چرخش برابر $$\large \theta = \frac {\beta} {2}$$ است. با جایگذاری این دو مقدار در رابطه قبل، شتاب پیرو به شکل زیر به دست می‌آید.

$$\large A = \frac {4h \omega^2} {\beta ^2}$$

در نتیجه، معادلات سرعت و جابجایی هم به راحتی قابل محاسبه خواهد بود.

$$\large V = At = \frac {4h\omega^2}{\beta^2} (\frac {\theta}{\omega}) \\~\\
\large s = 2h\frac {\theta ^2}{\beta^2}$$

به شیوه مشابه، برای حالتی که زاویه چرخش بادامک $$\large \theta \geq 0.5 \beta$$ باشد، معادلات سه‌گانه جابجایی، سرعت و شتاب به طریق زیر بیان می‌شود.

$$\large s = h[1 - 2(1-\frac {\theta}{\beta})^2] \\~\\
\large V = \frac {4h\omega}{\beta}(1-\frac {\theta}{\beta})\\~\\
\large A = - \frac {4h \omega^2} {\beta^2}$$

حرکت پیرو با سرعت ثابت اصلاح شده

حرکت با سرعت ثابت اصلاح شده به معنی این است که پیرو در بازه‌های زمانی مساوی، جابجایی‌های مساوی داشته باشد. بنابراین، نمودار جابجایی برحسب زمان به صورت خطوط راست خواهد بود. شکل زیر، نمودار جابجایی را برای پیروی نشان می‌دهد که از نقطه $$\large B$$ تا $$\large C$$ با سرعت ثابت بالا می‌رود. در فاصله $$\large C$$ تا $$\large D$$ ساکن است و از نقطه $$\large D$$ تا $$\large E$$ با سرعت ثابت پایین می‌آید. از لحاظ تئوری، این شیوه حرکت موجب می‌شود شتاب در این چهار نقطه بی‌نهایت شود. در نتیجه، بارگذاری از نوع ضربه خواهد بود. پس بهتر است از این نوع حرکت استفاده نشود.

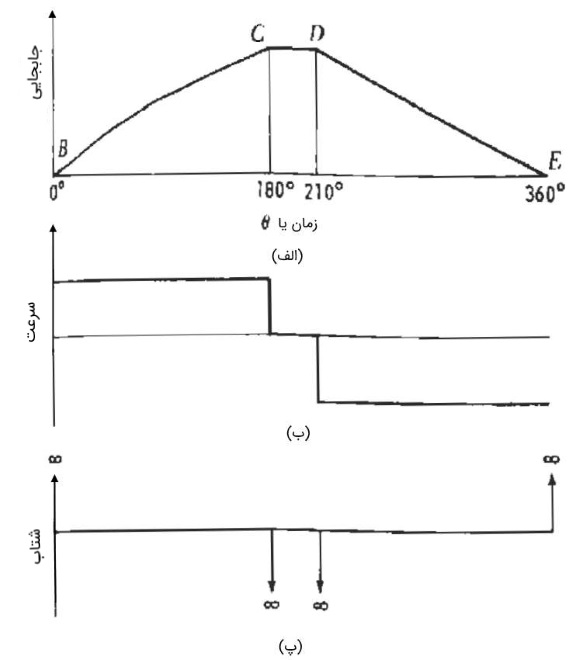
حرکت پیرو با سرعت اصلاح شده، شامل دو بازه زمانی هم می‌شود. در یکی، پیش از سرعت ثابت، شتاب مثبت است و در دیگری پس از سرعت ثابت، شتاب منفی خواهید بود. این موضوع را در مثال زیر بررسی می‌کنیم.

مثال

شکل زیر، نمودار جابجایی را نشان می‌دهد. فرض کنید پیرو تا رسیدن به زاویه چرخش 180 درجه، با سرعت ثابت اصلاح شده تا فاصله ۲ اینچ بالا می‌رود. در ۳۰ درجه بعدی ساکن است. ۶۰ درجه بعدی را با شتاب مثبت و بقیه مسیر (۹۰ درجه پایانی) را با شتاب منفی پایین می‌آید.

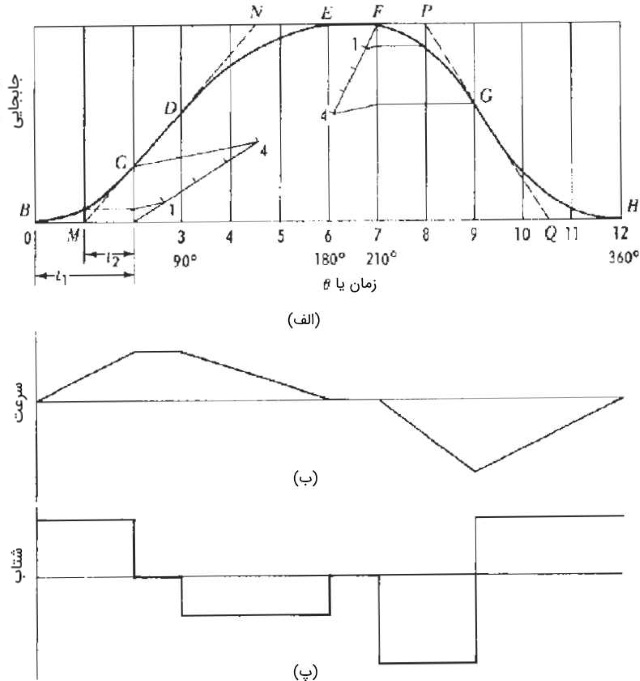
با توجه به شکل بالا درمی‌یابیم که 180 درجه اول، به سه قسمت تقسیم شده است. در ۶۰ درجه ابتدایی، پیرو شتاب مثبت دارد. در ۳۰ درجه بعدی، سرعت آن ثابت می‌ماند و پس از آن، شتاب منفی می‌گیرد. نقطه میانی بازه‌ای را که در آن شتاب مثبت است، با خط $$\large MN$$ به نقطه میانی بازه شتاب منفی وصل می‌کنیم. سرعت در انتهای منحنی $$\large BC$$ با سرعت خط $$\large CD$$ برابر است. می‌توان نشان داد که $$\large t_1$$ دو برابر $$\large t_2$$ است. بدین منظور، جابجایی و سرعت را برای نقطه $$\large C$$ می‌نویسیم. در حرکت با شتاب ثابت از $$\large B$$ تا $$\large C$$، روابط زیر برقرار است.

$$\large s = \frac {1} {2} At^2_1 ~~~ \Rightarrow ~~~ A = \frac {2s} {t^2_1}\\~\\
\large V= At_1 = \frac {2s} {t^2_1} \times t_1 = \frac {2s} {t_1}$$

برای حرکت با سرعت ثابت از نقطه $$\large M$$ تا $$\large C$$، جابجایی به صورت $$\large s = V \times t_2$$ است. با مقایسه دو رابطه به دست آمده برای سرعت، به راحتی می‌توان به نتیجه زیر رسید.

$$\large \frac {2s} {t_1} = \frac {s} {t_2}~~~ \Rightarrow ~~~~ t_1 = 2t_2$$

حرکت پیرو با هارمونیک ساده

ایده طراحی این مدل بدین صورت است که اگر حرکت نقطه $$\large P$$ با سرعت زاویه‌ای ثابت در مسیری دایره‌ای را روی قطر تصویر کنیم، حرکت هارمونیک ساده ایجاد شود. نمودار جابجایی برای حرکت هارمونیک ساده، در شکل زیر نشان داده شده است. یک دور چرخش کامل بادامک به اندازه $$\large \beta$$ موجب بالا رفتن پیرو به اندازه $$\large h$$ می‌شود. نیم‌دایره‌ای به شعاع $$\large h/2$$ روی محور عمودی رسم شده است. هم محور افقی و هم نیم‌دایره روی محور عمودی را مطابق شکل، به تعداد بازه مساوی تقسیم می‌کنیم. از تقاطع نقاط متناظر، منحنی شکل زیر را تشکیل می‌دهد.

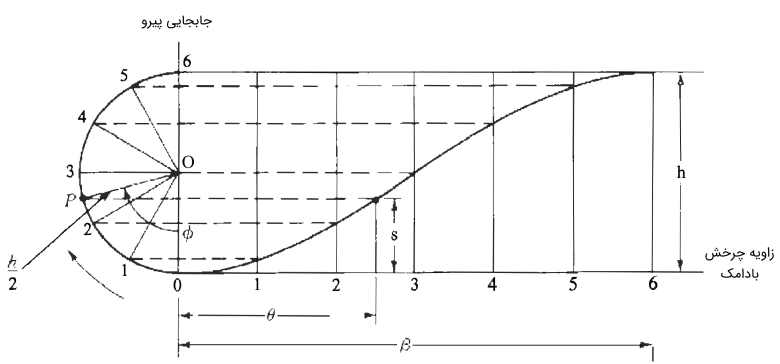
جابجایی نقطه $$\large P$$ روی محیط نیم‌دایره را با زاویه $$\large \phi$$ نشان می‌دهیم. تغییر این زاویه، منجر به تغییر زاویه $$\large \theta$$ و جابجایی $$\large s$$ می‌شود. با توجه به نمودار بالا، معادلات جابجایی، سرعت و شتاب به شیوه زیر به دست می‌آید.

$$\large s = \frac {h}{2} - \frac {h}{2}\cos\phi = \frac {h}{2} (1-\cos\phi)\\~\\
\large \frac {\phi}{\pi} = \frac {\theta} {\beta}\\~\\
\large \Rightarrow ~~~ s=\frac {h}{2} (1 - \cos \frac {\pi \theta}{\beta})\\~\\
\large \Rightarrow V=\frac {\pi h \omega}{2 \beta} \sin \frac {\pi \theta}{\beta}\\~\\
\large \Rightarrow A = \frac {\pi ^2 h \omega ^2}{2 \beta ^2} \cos \frac {\pi \theta}{\beta}$$

حرکت پیرو به صورت سیکلوئیدی

در این حالت، نمودار جابجایی حرکت پیرو به صورت سیکلوئید یا چرخ‌زاد است. اگر دایره‌ای روی یک خط مستقیم بغلتد، مکان هندسی نقطه‌ای که روی دایره قرار دارد، تشکیل یک سیکلوئید می‌دهد. به شکل زیر توجه کنید. در سمت راست نمودار، دایره‌ای به محیط $$\large h$$ روی خط مستقیم $$\large FE$$ می‌غلتد. مسیر حرکت نقطه‌ای روی دایره، منحنی $$\large FHE$$ را تشکیل داده است. به این منحنی یک سیکلوئید می‌گوییم. زاویه $$\large \phi$$ در این دایره، با چرخش بادامک به اندازه $$\large \theta$$ متناظر است. با دقت در شکل، می‌توان جابجایی $$\large s$$ را به صورت زیر نوشت.

$$\large s = R\phi - R \sin \phi = R(\phi - \sin \phi)$$

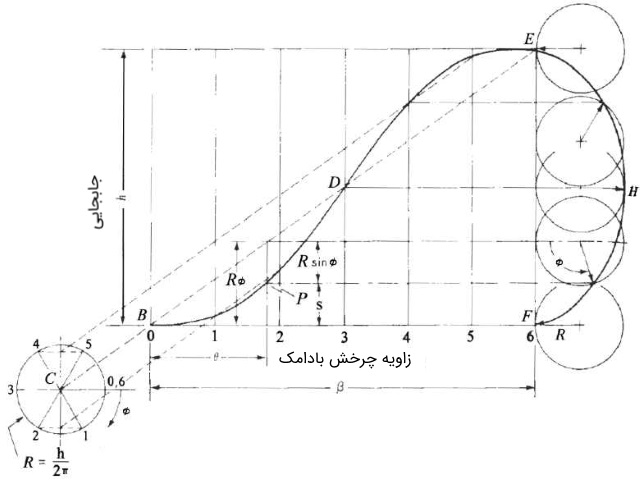
با توجه به تغییر زاویه $$\large \phi$$ و ارتفاع $$\large h$$، معادله جابجایی به دست می‌آید. سپس با مشتق‌گیری از این رابطه، می‌توان سرعت و شتاب را به دست آورد.

$$\large \phi = 2\pi \frac {\theta} { \beta}, ~~~ R= \frac {h}{2\pi}\\~\\
\large s = \frac {h} {2\pi} (2\pi \frac {\theta}{\beta} - \sin 2\pi{\theta}{\beta}) = h\frac {\theta}{\beta} - \frac {h}{2\pi} \sin 2\pi \frac {\theta}{\beta} \\~\\
\large V = \frac {h}{\beta} \omega (1 - \cos \frac {2 \pi \theta}{\beta}) \\~\\
\large A = \frac {2 \pi h}{\beta ^2} \omega ^2 \sin \frac {2\pi \theta}{\beta}$$

دسته‌بندی پیرو بر اساس نوع سطح تماس

غیر از مواردی که تا اینجا گفته شد، می‌توان دسته‌بندی دیگری هم برای پیرو در نظر گرفت. در شکل زیر، انواع پیرو براساس سطح تماس بین بادامک و پیرو نشان داده شده است.

فیلم آموزش بررسی انواع یاتاقان ها با نرم افزار Adams Machinery (رایگان) در فرادرس

کلیک کنید

در ادامه، انواع پیرو را بررسی می‌کنیم.

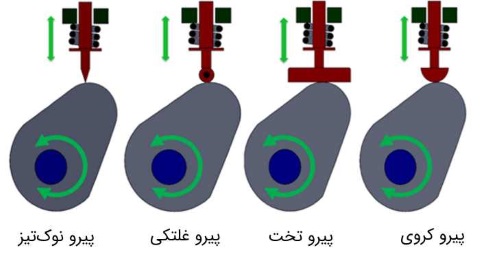
پیرو نوک‌تیز

پیرو نوک‌تیز (knife edge follower)، همان‌طور که از نام آن هم برمی‌آید، دارای انتهای نوک‌تیز است. بین سطح تماس بادامک و پیرو، حرکت لغزشی وجود دارد. در عمل به ندرت از این پیرو استفاده می‌شود. زیرا کوچک بودن ناحیه تماس، موجب سایش شدید بادامک می‌شود و این مدل، بیشتر به عنوان یک مدل تئوری به شمار می‌رود.

پیرو غلتکی

پیرو غلتکی (roller follower)، یکی از انواع پرکاربرد پیرو است. این نوع پیرو، از یک غلتک استوانه‌ای تشکیل شده که روی سطح بادامک می‌غلتد. به خاطر حرکت غلتشی بین سطوح تماس، نرخ سایش در مقایسه با پیرو نوک‌تیز، به شدت کاهش می‌یابد. در کاربردهایی که فضای بیشتری در دسترس باشد، این پیروها به طور وسیع به کار می‌روند.

پیرو تخت

پیرو تخت (flat face follower)، نوع دیگری از پیروها محسوب می‌شود. صفحه تختی در انتهای پیرو قرار گرفته و تماس از این ناحیه انجام می‌شود. در اینجا هم نوع حرکت از نوع لغزشی است. در نتیجه اصطکاک نسبت به پیرو غلتکی، خیلی بیشتر است. در کاربردهایی که نیاز به حرکت سریع باشد، از پیرو تخت استفاده می‌شود. با این وجود، هرگونه ناهمترازی یا انحراف در پیرو، باعث ایجاد تنش‌های شدید سطحی می‌شود. یکی از نقاط ضعف این پیرو، نیروی تراست (Thrust) جانبی است که به دلیل وجود اصطکاک در سطح تماس، وارد می‌شود.

پیرو کروی

همچنین در برخی از دسته‌بندی‌ها، نوع دیگری هم گنجانده شده است که تحت عنوان پیرو کروی (spherical face follower) شناخته می‌شود. سطح تماس پیرو با بادامک، به شکل بخشی از یک کره است. همین ساختار کروی، از ایجاد نیروی تراست جانبی جلوگیری می‌کند. این سطح کروی، همچنین قادر است انحراف و ناهمترازی‌ها را خنثی کند. ولی باز هم به دلیل ماهیت تماس، نسبت به پیرو غلتکی، اصطکاک بسیار بیشتری دارد.

زاویه فشار

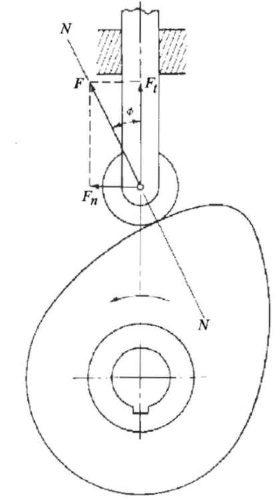
زاویه بین خط عمود مشترک در نقطه تماس بادامک و پیرو و مسیر حرکت پیرو، زاویه فشار نامیده می‌شود. در شکل زیر، زاویه فشار با نماد $$\large \phi$$ نشان داده شده است. نیروی $$\large F$$ نیرویی است که بادامک به پیرو وارد می‌کند. این نیرو به دو مؤلفه $$\large F_t$$ در جهت مماسی و $$\large F_n$$ در جهت عمودی تقسیم شده است. این دو جهت، نسبت به مسیر حرکت پیرو سنجیده می‌شود. مؤلفه عمودی، یک نیروی تراست جانبی ناخواسته است. همان‌طور که از شکل به نظر می‌رسد، با کم کردن زاویه فشار، می‌توان این نیرو را کاهش داد. در طراحی‌ها برای عملکرد بهتر، زاویه فشار از ۳۰ درجه فراتر نمی‌رود. ولی اگر مقدار نیرو، کوچک باشد و یاتاقان‌ها دقیق عمل کنند، می‌توان زاویه‌ فشار را بیشتر از این هم انتخاب کرد.

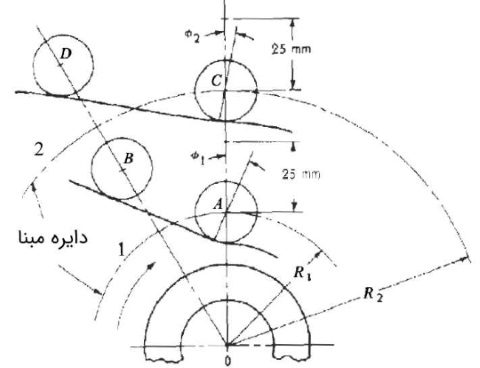
بزرگ شدن دایره مبنا، زاویه فشار را کاهش می‌دهد. شکل زیر را در نظر بگیرید. بالا رفتن از نقطه $$\large A$$ تا $$\large B$$ برابر با بالا رفتن از نقطه $$\large C$$ تا $$\large D$$ است. در دایره مبنای کوچکتر که با شماره ۱ دیده می‌شود، زاویه فشار برابر $$\large \phi_1$$ است. زاویه فشار در دایره بزرگتر هم $$\large \phi_2$$ نام دارد. این دایره را با شماره ۲ مشاهده می‌کنید. آنچه به وضوح از شکل برمی‌آید، این است که رابطه $$\large \phi_2 < \phi_1$$ برقرار است.

وقتی نمودار جابجایی مشخص باشد، برای کاهش زاویه فشار می‌توان یکی از موارد زیر را به کار برد.

• افزایش قطر دایره مبنا
• کاهش ارتفاع حرکتی پیرو
• افزایش زاویه چرخش بادامک برای جابجایی مشخص پیرو
• تغییر نوع حرکت پیرو
• تغییر میزان آفست (Offset)‌ در پیرو

کاربرد بادامک

بادامک‌ها کاربردهای بسیار زیادی دارند. به عنوان نمونه می‌توان به مواردی از قبیل اتوماسیون ماشین‌آلات، صنایع نساجی، ماشین‌های خیاطی خانگی، نوار نقاله، دستگاه‌های پرس، دستگاه‌های برش‌دهنده چرخ‌دنده و ماشین تراش اشاره کرد. بادامک‌ها در موتورهای احتراق داخلی هم کاربرد زیادی دارند. در این موتورها برای باز و بسته کردن دریچه‌های ورودی و خروجی سوخت و هوا، از بادامک‌ها استفاده می‌شود. این موضوع در شکل زیر نشان داده شده است.

در ماشین تراش، محور بادامک توسط یک موتور به حرکت در می‌آید. ابزار تراشنده‌ روی لغزنده جانبی نصب شده است. با استفاده از بادامک‌های دیسکی که روی محور سوار شده‌اند، می‌توان عمق و همچنین سرعت رفت و برگشت ابزار تراشنده را تنظیم کرد. به این محور که بادامک‌ها روی آن سوار شده‌اند، میل بادامک (Cam Shaft) گفته می‌شود.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• چرخ دنده – به زبان ساده
• چرخ دنده ساده – از صفر تا صد
• نسبت چرخ دنده — به زبان ساده

^^