فرادرسانرژی موج — از صفر تا صد
اگر مطالب میدان‌های الکتریکی و مغناطیسی را مطالعه کرده باشید، می‌دانید که این میدان‌ها حاوی انرژی هستند. با توجه به این که یک موج الکترومغناطیسی از دو میدان عمود بر هم تشکیل شده، بنابراین یک موج الکترومغناطیسی نیز حاوی انرژی است. از این رو در این مطلب قصد داریم تا در مورد نحوه محاسبه انرژی موج الکترومغناطیسی صحبت کرده و ارتباط آن با دامنه میدان‌ها را توضیح دهیم.
انرژی موج الکترومغناطیسی
احتمالا همه شما از مایکرویو استفاده کرده‌اید. همان‌طور که احتمالا می‌دانید این دستگاه‌ها مبتنی بر انتقال انرژی ذخیره شده در امواج الکترومغناطیسی کار می‌کنند. در حقیقت هر موج الکترومغناطیسی دارای انرژی بوده و با منتقل شدن این انرژی به درون مواد، منجر به گرم شدن آن می‌شود. انرژی ذخیره شده در امواج در بعضی مواقع واضح هستند. برای نمونه اگر در تابستان در معرض نور خورشید قرار داشته باشید، انرژی تابش شده روی پوستتان را به خوبی حس خواهید کرد.
اگر مطلب موج الکترومغناطیسی را مطالعه کرده باشید خواهید دانست که این امواج از دو میدان مغناطیسی و الکتریکی عمود بر هم تشکیل شده‌اند. از طرفی این میدان‌ها حاوی انرژی هستند. در حقیقت انرژی یک موج الکترومغناطیسی همان انرژی نهفته در میدان‌های عمود بر هم هستند. هرچه دامنه میدان‌های الکتریکی و مغناطیسی بیشتر باشند، در این صورت انرژی ذخیره شده در موج الکترومغناطیسی مرتبط با آن نیز بیشتر است. در یک موج الکترومغناطیسی مقدار انرژی وابسته به فرکانس و دامنه میدان‌های الکتریکی و مغناطیسی است.
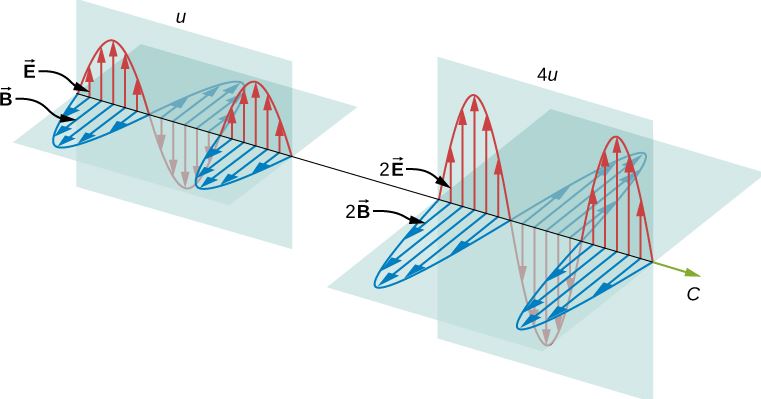
ارتباط انرژی با دامنه
میدان‌های الکتریکی و مغناطیسی منتشر شده را معمولا به صورت متناوب در نظر می‌‌گیرند. برای نمونه معادلات زیر می‌تواند توصیف‌کننده دو میدان الکتریکی و مغناطیسی باشد.
$$ \begin {aligned} \color {white} { E _ { y } ( x , t ) } E _ { y } ( x , t ) & = E _ { 0 } \cos ( k x - \omega t ) \\ B _ { x } ( x , t ) & = B _ { 0 } \cos ( k x - \omega t ) \color {white} { E _ { y } ( x , t ) } \end {aligned} $$
انرژی منتقل شده در هر بخش از یک موج الکترومغناطیسی برابر با حاصل جمع انرژی نهفته در میدان الکتریکی و میدان مغناطیسیِ موج است. معمولا به جای بررسی خود انرژی از چگالی انرژی استفاده می‌شود. اگر چگالی انرژی با $$ u $$ نشان داده شود، در این صورت چگالی انرژی کل قرار گرفته در یک بخش از موج الکترومغناطیسی را می‌توان با استفاده از رابطه زیر محاسبه کرد.
$$ u ( x , t ) = u _ { E } + u _ { B } = \frac { 1 } { 2 } \epsilon _ { 0 } E ^ { 2 } + \frac { 1 } { 2 \mu _ { 0 } } B ^ { 2 } $$
$$ ϵ _ 0 $$ نشان‌دهنده ضریب گذردهی و $$ \mu _ 0 $$ نیز تراوایی مغناطیسی را نشان می‌دهد. در حالتِ $$ E = c B = \frac { 1 } { \sqrt { \epsilon _ 0 \mu _ 0 } } B $$، چگالی انرژی مغناطیسی و چگالی انرژی الکتریکی با هم برابر هستند. در این حالت مقدار چگالی انرژی برابر است با:
$$ u ( x , t ) = \epsilon _ 0 E ^ 2 = \frac { B ^ 2 } { \mu _ 0 } $$
حال استوانه‌ای را به شکل زیر در نظر بگیرید. طول این استوانه برابر با $$ c Δ t $$ (طول این استوانه برابر با مسافتی در نظر گرفته شده که نور با سرعت $$ c $$ می‌کند) و سطح مقطع آن نیز برابر با $$ A $$ است.
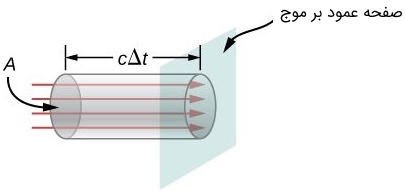
در این صورت میزان انرژی عبوری از استوانه فوق، در زمان $$ \Delta t $$ برابر است با:
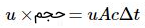
مقدار انرژی عبوری، در واحد زمان که از سطح عمود به جهت موج (جبهه موج) عبور می‌کند، تحت عنوان چگالی انرژی شناخته شده و آن را به صورت حاصل تقسیم زیر نشان می‌دهند.
به طور کلی‌تر می‌توان گفت که شار انرژی نیز وابسته به جهت بردار عمود بر صفحه است. به منظور اعمال کردن تاثیر این جهت، از برداری تحت عنوان پوئینتینگ استفاده می‌شود. این بردار با استفاده از ضرب خارجی زیر تعریف می‌شود.
$$ \overrightarrow { S } = \frac { 1 } { \mu _ 0 } \overrightarrow { E } \times \overrightarrow { B } $$
بدیهی است که بردار فوق به هر دو بردار میدان الکتریکی و مغناطیسی عمود است. با توجه به میدان کسینوسی در نظر گرفته شده برای میدان الکتریکی و مغناطیسی، بردار شار انرژی یا همان $$ S $$ برابر است با:
$$ \color {white} { { S ( x , t ) = c \epsilon _ { 0 } E _ { 0 } ^ { 2 } \cos ^ { 2 } ( k x - \omega t ) } } S ( x , t ) = c \epsilon _ { 0 } E _ { 0 } ^ { 2 } \cos ^ { 2 } ( k x - \omega t ) \color {white} { { S ( x , t ) = c \epsilon _ { 0 } E _ { 0 } ^ { 2 } \cos ^ { 2 } ( k x - \omega t ) } } $$
برای درک رابطه فوق نور را در نظر بگیرید. همان‌طور که احتمالا می‌دانید فرکانس نور، عددی بالا و در حدود $$ 1 0 ^ { 14 } H z $$ است. از این رو شار انرژی گذرنده از یک سطح که ناشی از پرتو نور است، با سرعت بسیار زیادی تغییر می‌کند. بسیاری از دستگاه‌های اندازه‌گیری از جمله چشم انسان، در یک بازه زمانی، مقداری متوسط از این انرژی را اندازه‌گیری می‌کنند.
با توجه به فرکانس بالای موج، از مفهومی تحت عنوان شدت موج استفاده می‌کنند. شدت موج یا $$ I $$ نشان‌دهنده میانگین انرژی است که از واحد سطح عبور می‌کند. برای محاسبه شدت باید میانگین بردار پوئینتیگ را در یک دوره زمانی بدست آوریم. از این رو می‌توان از انتگرال استفاده کرد. در نتیجه شدت یک موج با دوره تناوب $$ T $$ برابر است با:
$$ I = S _ { a v g } = c \epsilon _ 0 E _ 0 ^ 2 \frac { 1 } { T } \int _ 0 ^ T cos ^ 2 \, \left( 2 \pi \frac { t } { T } \right) d t $$
میانگین توان دوم تابعی سینوسی یا کسینوسی برابر با $$ \frac { 1 } { 2 } $$ است (در یک دوره تناوب). از این رو حاصل انتگرال فوق برابر می‌شود با:
$$ I = S _ { a v g } = \frac { 1 } { 2 } c \epsilon _ 0 E _ 0 ^ 2 $$
رابطه فوق بر حسب ماکزیمم مقدار میدان الکتریکی بیان شده است. این رابطه را می‌توان بر حسب ماکزیمم مقدار میدان مغناطیسی، به صورت زیر بیان کرد:
$$ I = \frac { c B _ 0 ^ 2 } { 2 \mu _ 0 } $$
با استفاده از رابطه $$ c B _ 0 = E _ 0 $$، می‌توان مقدار شدت را همزمان بر حسب ماکزیمم میدان مغناطیسی و الکتریکی بیان کرد:
$$ I = \frac { E _ 0 B _ 0 } { 2 \mu _ 0 } $$
توجه داشته باید که بسته به نوع مسئله، می‌توان هریک از سه رابطه فوق را استفاده کرد.
مثال ۱
فرض کنید که شدت نور یک لیزر در حدود $$ 1 . 0 \times 1 0 ^ { - 3 } W / m ^ 2 $$ باشد. دامنه میدان الکتریکی و مغناطیسی این موج را بیابید.
با توجه به رابطه $$ I = \frac { 1 } { 2 } c \epsilon _ 0 E _ 0 ^ 2 \nonumber $$، دامنه میدان الکتریکی برابر است با:
$$ \begin {align*} E _ 0 & = \sqrt { \frac { 2 } { c \epsilon _ 0 } I } \\[4pt] & = \sqrt { \frac { 2 } { ( 3 .00 \times 10^8 m / s ) ( 8.85 \times 10 ^ {-12} F / m ) } \left( 1.0 \times 10^{-3} V / m ^ 2 \right) } \\[4pt] & = 0.87 \, V / m. \end {align*}$$
در نتیجه دامنه میدان مغناطیسی نیز به صورت زیر و به راحتی قابل محاسبه است.
$$ B _ 0 = \frac { E _ 0 } { c } = 2.9 \times 10 ^ { - 9 } \, T \nonumber $$
مثال ۲
مطابق با شکل زیر فرض کنید یک لامپ $$ 5 W $$ در یک اتاق روشن است. دامنه میدان الکتریکی و مغناطیسی نور ناشی از این لامپ در فاصله $$ 3 $$ متر چقدر است.
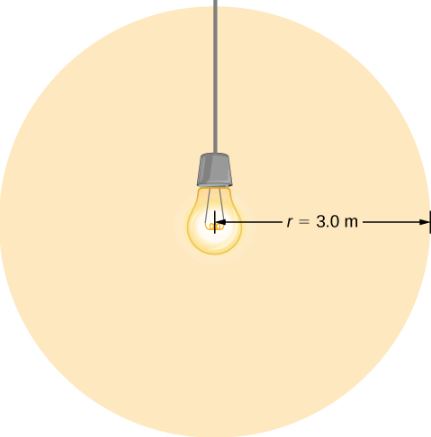
انرژی در نتیجه نور مرئی تابش می‌شود. بنابراین دامنه میدان الکتریکی برابر می‌شود با:
$$ I = \frac { P } { 4 \pi r ^ 2 } = \frac { c \epsilon _ 0 E _ 0 ^ 2 } { 2 } $$
$$ E _ 0 = \sqrt { 2 \frac { P } { 4 \pi r ^ 2 c \epsilon _ 0 } } = \sqrt { 2 \frac { 5 . 0 0 \, W } { 4 \pi (3.0 \, m ) ^ 2 (3.00 \times 10 ^ 8 \, m / s ) ( 8.85 \times 10 ^ { - 1 2 } C ^ 2 / N \cdot m ^ 2 ) } } = 5.77 \, N / C,$$
در نتیجه دامنه میدان مغناطیسی نیز برابر است با:
$$ B _ 0 = E _ 0 / c = 1 . 92 \times 10 ^ { - 8 } \, T $$
مثال ۳
یک فرستنده رادیویی $$ 60 kW $$، سیگنالی را به سمت یک ماهواره که در فاصله ۱۰۰ کیلومتری زمین قرار گرفته، می‌فرستد. اگر قدرت سیگنال به $$ 90 kW $$ افزایش یابد، در این صورت در چه فاصله‌ای، دامنه میدان برابر با حالت اولیه است (جهت ارسال موج را در هر دو حالت یکسان در نظر بگیرید).
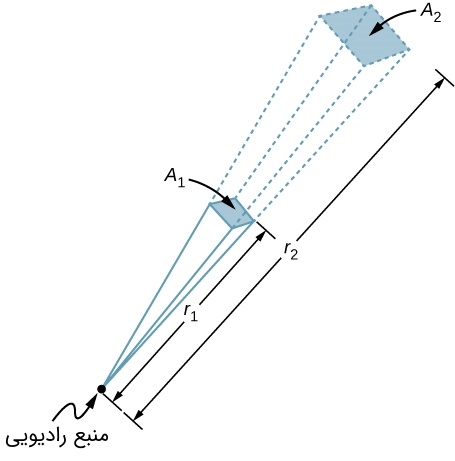
همان‌طور که در تصویر فوق نیز نشان داده شده، با افزایش فاصله از منبع انتشار، میزان انرژی قرار گرفته در جبهه نیز زیاد می‌شود. ثابت ماندن دامنه میدان به معنای ثابت ماندن عبارت زیر است.
$$ I = \frac { P } { A } = \frac { c \epsilon _ 0 E _ 0 ^ 2 } { 2 } $$
بنابراین فاصله در حالت دوم برابر است با:
$$ \begin {align*} \frac { r _ 2 ^ 2 } { r _ 1 ^ 2 } &= \frac { A _ 2 } { A _ 1 } = \frac { 90 \, W } { 60 \, W }, \\[4pt] r _ 2 & = \sqrt {\left( { \frac { 9 0 } {6 0} } \right)} ( 100 \, km) \\[4pt] &= 122 \, km. \end{align*} $$
در صورتی که مطلب فوق برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
