اعداد گنگ – به زبان ساده
در مطالب گذشته مجله فرادرس اعداد گویا و اعداد حقیقی را معرفی کردیم. در این بخش نیز قصد داریم تا عددی را معرفی کنیم که به نحوی مخالف عدد گویا است. این اعداد تحت عنوان اعداد گنگ شناخته و دستهبندی میشوند.


تعریف عدد گنگ
در ریاضیات به بخشی از اعداد حقیقی، اعداد گنگ یا اصم گفته میشود که گویا نباشد. در حقیقت عدد گنگ مقداری حقیقی است که نمیتوان آن را به صورت یک کسر با مقادیر صورت و مخرج حقیقی بیان کرد.
بهمنظور بررسی، عدد ۱.۵ را در نظر بگیرید. این عدد را میتوان مطابق با عبارت زیر بهصورت یک کسر بیان کرد:
همانطور که مشاهده کردید این عدد را میتوان بهصورت یک کسر با مقادیر صورت و مخرج صحیح بیان کرد. از این رو ۱.۵ عددی گویا است. اما عددی همچون را در نظر بگیرید. همانطور که احتمالا میدانید این عدد در مقادیر اعشاریش، الگویی تکرارنشدنی دارد که مانع از نوشتن این مقدار بهصورت کسری میشود. بنابراین میتوان گفت:

در نتیجه عدد فوق عددی گنگ محسوب میشود. در ادامه مقدار تا ۱۰۰۰ رقم اعشار نشان داده شده است.

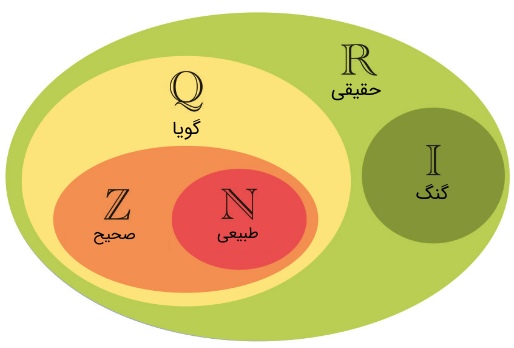
همانطور که مشاهده میکنید الگویی مشخص میان اعداد پشت اعشار وجود ندارد. در ادامه جایگاه اعداد مختلف در مجموعه اعداد حقیقی نشان داده شده است.
مثال
از بین سه مقدار ۱.۷۵، ۰.۰۰۱ و ، کدامیک گنگ و کدامیک گویا هستند؟
همانطور که بیان شد در مواجه با یک عدد در ابتدا در نظر بگیرید که آیا میتوان عدد مذکور را بهصورت کسری نوشت. یکی از راهها این است که عدد مذکور را در مقادیر غیرصفر و صحیح ضرب کنید و ببینید که آیا به عدد صحیحی میرسید؟ اگر به عدد صحیحی دست یافتید عدد مذکور گویا است. برای نمونه عدد ۱.۷۵ را در نظر بگیرید. با ضرب کردن این عدد در اعدادِ صحیح مختلف داریم:
$$ \begin {align*} \require {color} 1.75 × 1 & = 1.75 \\ 1.75 × 2 & = 3 . 5 \\ 1 . 7 5 × 3 & = 5.25 \\ \large 1.75 × 4 & = \large \color {red} 7 \end {align*} $$
همانطور که میبینید با ضرب کردن ۱.۷۵ در عدد صحیح ۴ به عدد صحیح ۷ میرسیم. از این رو میتوان این عدد را بهصورت زیر بیان کرد:
بنابراین این عدد گویا محسوب میشود. توجه داشته باشید که به منظور بررسی ۰.۰۰۱ نیازی نیست از ۱ تا ۱۰۰۰ را در این عدد ضرب کنید و ببینید آیا عددی صحیح بدست میآید یا خیر؟ در حقیقت میتوان در نگاه اول متوجه شد که یک هزارم را میتوان به صورت زیر نوشت:
بنابراین نیز عددی گویا محسوب میشود. به نظر شما میتوان عددی پیدا کرد که با ضرب کردن آن در به عددی صحیح دست یافت؟ پاسخ منفی است. به جرات میتوان گفت مشهورترین عدد گنگ موجود، است.
اعداد گنگ شناخته شده
در فیزیک و ریاضیات اعدادی گنگ وجود دارند که از آنها زیاد استفاده شده و به دفعات مشاهده میشوند.
در ادامه قصد داریم تا معروفترین این اعداد را معرفی کنیم.
عدد
بسیاری معتقدند اولین عدد گنگ کشف شده عدد است که توسط شاگرد فیثاغورس کشف شد. این عدد برابر با وتر یک مثلث متساویالساقین با طول اضلاع ۱ یا قطر یک مربع با طول اضلاع ۱ محسوب میشود. در شکل زیر مثلث مذکور نشان داده شده است.
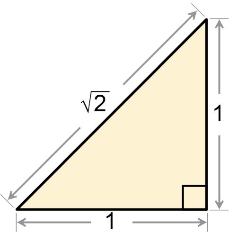
مقدار این عدد نیز برابر است با:
همانطور که مشاهده میکنید برای نوشتن از سه نقطه استفاده کردیم. دلیل این امر آن است که برای این عدد نیز نمیتوان الگوی مشخصی را برای اعداد پشت اعشار بیان کرد. جالب است بدانید است با استفاده از میتوان گنگ بودن بسیاری دیگر از اعداد رادیکالی را نیز اثبات کرد.
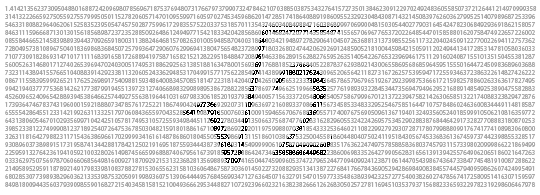
عدد طلایی ()
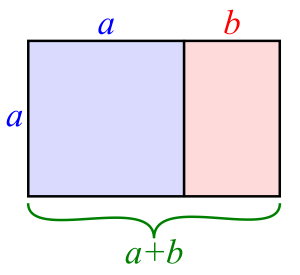
عدد فی یا نسبت طلایی عددی در ریاضیات و فیزیک است که زمانی بدست میآید که نسبت طول بخش بزرگتر به طول بخش کوچکتر برابر با نسبت کل طول به بخش بزرگتر باشد. برای درک بهتر شکل زیر را در نظر بگیرید.
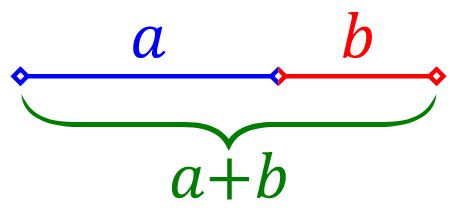
با توجه به اندازههای ارائه شده در بالا میتوان گفت زمانی نسبت طلایی بدست میآید که رابطه زیر بین طولها برقرار باشد.
مقدار دقیق نسبت طلایی برابر با بوده و مقدار تقریبی آن نیز برابر با است. نکتهای بسیار جالب در مورد نسبت طلایی این است که زیبایی و چشم نوازی بسیاری از طراحیها با این عدد در ارتباط است. در شکل زیر مستطیل طلایی نشان داده شده است. در حقیقت نسبت طول به عرض این مستطیل برابر با نسبت طلایی است. میتوان گفت مستطیلی با این نسبت به نحوی چشمنوازترین مستطیل ممکن محسوب میشود.
عدد اویلر ()
عددی مشخص و یکتا با مقداری حقیقی است. این عدد برابر با مقداری است که با انتخاب تابع بهصورت زیر، مشتق آن در نقطه برابر با بدست میآید.
تابع معکوس فوق نیز در مبنای محاسبه شده و آن را بهصورت لگاریتم طبیعی بیان میکنند. این عدد را به یاد ریاضیدان سوییسی، لئونارد اویلر، عدد اویلر نامیدهاند. البته در مواردی این عدد را ثابت نپر نیز مینامند. عدد نپر در بسیاری از شاخههای ریاضی، فیزیک و حتی آمار مشاهده میشود. با استفاده از نظریه اعداد مختلط میتوان بین این عدد و عدد ارتباط برقرار کرد. به عنوان مثال تساوی زیر نمونهای از این ارتباط را نشان میدهد.
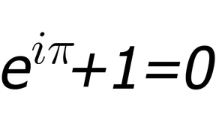
آزمون اعداد گنگ
۱. کدام ویژگی باعث میشود یک عدد را گنگ بدانیم و نه گویا؟
میتوان عدد را دقیقا روی عدد صحیح جای داد.
وجود الگوی تکراری در بخش اعشاری عدد.
امکان نوشتن عدد به صورت کسری با اعداد صحیح وجود ندارد.
عدد شامل رقم اعشاری کمتر از ۹ باشد.
عدد گنگ عددی است که نمیتوان آن را با استفاده از یک کسر حاوی اعداد صحیح نشان داد. این ویژگی باعث تفاوت آن با عدد گویا میشود، چون اعداد گویا برعکس اعداد گنگ، همیشه به صورت کسر با صورت و مخرج صحیح نوشته میشوند.
۲. چطور میتوان عدد اعشاری ۱٫۷۵ را به عنوان یک عدد گویا تشخیص داد؟
با مشاهده بخش اعشاری پایانناپذیر در ۱٫۷۵
با ضرب ۱٫۷۵ در عدد پی
با نوشتن ۱٫۷۵ به صورت کسر ساده
با تبدیل ۱٫۷۵ به عدد گنگ مانند ریشه ۲
روش تشخیص گویا بودن عددی مانند ۱٫۷۵ این است که بتوان آن را به صورت یک کسر با صورت و مخرج صحیح نوشت. این امکان فقط برای اعدادی وجود دارد که اعشاریشان پایانیافته باشد.
۳. کدام ویژگی درباره کاربرد اعداد گنگ مشهوری مانند π، √۲، φ و e در ریاضیات و هندسه درست است؟
√۲، π، φ و e فقط به صورت اعشاری بیپایان نمایش داده میشوند و کاربرد مشترک ندارند.
π و φ در بیشتر مسائل هندسی کاربرد دارند، اما e بیشتر در ریاضیات پیشرفته است.
تمام این اعداد فقط در هندسه و طراحی ظاهر میشوند.
e و π تنها در فیزیک استفاده میشوند و در هندسه کاربرد ندارند.
π و φ هر دو ارتباط زیادی با هندسه و طراحی دارند (مثل رابطه طلایی و مساحت دایره)، در حالی که e غالبا در مباحث ریاضی مانند تابع نمایی و مشتق مطرح میشود و نه موضوعات هندسی.













سلام ببخشید اینکه ریاضی دانان مجموعه اعداد گنگ رو به دوتا زیر مجموعه افراز کردند ، میشه به نماد ریاضی بگیدشون؟
سلاممجیدجانمطالبتزیباوپربارممنون
دوستدارتعثمانعزیزیازسنندج
آیا کسری با صورت ٠ و مخرج ۵ عددی اول است؟
یا آیا عددی با مخرج ۰ و صورت ۲ باز اول است؟
اگه میشه یه کم زودتر جواب بدید ممنون میشم!
کسر با صورت ۰ همون ۰ میشه. مخرج مهم نیست. کسر با مخرج صفر، یه عبارت ریاضی تعریف نشده است.
سلام در قسمت مثال ها در ابتدا 1.75 ضرب در 3 برابر با 5.25 می شود.
نمودار ون رسم شده درباره ی اعداد طبیعی و صحیح و گنگ و گویا اشتباه است. هر عددی که گویا نباشد گنگ است اما در این نمودار اعداد گنگ محدود به یک بخش از اعداد حقیقی منهای اعداد گویا شده که اشتباه است
با سلام؛
مجموعه اعداد گنگ و گویا، بخشی از مجموعه اعداد حقیقی هستند. برای نمایش این موضوع، باید این دو مجموعه را به طور جداگانه درون مجموعه اعداد حقیقی قرار داد. اگر قسمت مد نظر شما (بخش سبز کمرنگ) را هم به عنوان مجموعه اعداد گنگ در نظر بگیریم، نمودار به اشتباه مجموعه اعداد گویا را به عنوان زیرمجموعه اعداد گنگ نمایش میدهد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
یه سوال اگه رادیکال دو ضربدر رادیکال دو بشه که جواب ۲ میشه و عدد صحیح درمیاد که..درصورتی که توی متن گفت عددی نیست که ضربدر رادیکال دو بشه و جواب عدد صحیح دربیاد
با سلام؛
منظور، عددی به غیر از عدد مورد بررسی است که امکان نوشتن آن به صورت کسری وجود داشته باشد. در اینجا قصد داریم گنگ بودن یا نبودن عدد را بررسی کنیم. بنابراین، استفاده از آن عدد، پیش از اطمینان از گنگ بودن یا نبودن آن درست نیست.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام.
متن بازبینی و اصلاح شد.
سپاس از همراهی و بازخوردتان.
عدد p ساخته ی خود انسانه چطور تا هنوز اخرش پیدا نشده؟
خب نسبت فطر یک دایره به محیطش مگه خودش کسر نیست؟!؟!؟!پس چرا گنگه؟!
سلام ببخشید یک عدد به توان گنگ چجوری محاسبه میشه
اعداد کشف میشن اختراع یا ابداع نمیشن که بشه گفت انسان ساختتش
یه نسبتی بین قطر یک دایره و محیطش بوده که دیسکاور شده وسسلام
چطوری میتونم این رو به صورت pdf دانلود کنم؟؟
درود بر شما.عالی بود
بسته بودن اعداد گنگ هم توضیح بدید
یبار معلممون گفت اگر روی محور اعداد حقیقی، یک عدد رو بصورت شانسی انتخاب کنید، به احتمال 100 درصد اون عدد گنگه ?
چطوری؟! مگه میشه؟! درسته هر دو بی نهایتن ولی گویا ها بنظر خیلی بیشتر میان
یا دیگه حداقل 50-50
چطور ممکنه یه عدد شانسی روی محور اعداد حقیقی انتخاب کنیم و به احتمال 100 درصد اون گنگ باشه!؟!؟!
گفت برین دنبال اثباتش ولی هرچی گشتم چیزی پیدا نکردم
میشه یکی بگه؟!؟!
مغزم داره میترکه
تعداد اعداد گنگ بینهایته و گویا هم بینهایته ولی بینهایت گنگ بسیار بسیار بسیار بزرگتر از بینهایت گویاست
درود ، از ملا نصرالدین پرسیدن مرکز زمین کجاست ، یک میخ در همانجا روی زمین کوبید وگفت اینجا ، نمی خواهید برید اندازه بگیرید.
خب راست گفته نکته کار همان محور است
ممکن نیست مثلا عدد دقیقا وقتی دست میزارید ۶۴ باشه ممکنه ۵۵.۸۷۶۹۶۵۹۵۷۹۵۸۹۶۷۹۷۷…… الی آخر باشه
۱۰۰ درصد که اغراقه
ولی ۵۰ ۵۰ خیلی کمه واسه اعداد گنگ !
شما بین دو عدد میتونید بی نهایت عدد گنگ پیدا کنید شاید بنظرم ۷۵ به ۲۵ باشه .
سلام اعداد گنگ چند دسته هستند
عالی بود مرسی