گذردهی الکتریکی – به زبان ساده

در آموزش‌های قبلی مجله فرادرس، درباره میدان الکتریکی صحبت کردیم. در این آموزش قصد داریم «گذردهی الکتریکی» (Permitivity) را بررسی کنیم. در بخش مقدماتی، ساختار اتم و مولکول ماده را بررسی می‌کنیم. سپس به بررسی قطبیت در مواد می‌پردازیم و در پایان به معرفی یکی از خواص الکتریکی ماده یعنی گذردهی الکتریکی می‌پردازیم.

مقدمه

اتم یک عنصر، از یک هسته فشرده و تعدادی الکترون با بار منفی تشکیل می‌شود. الکترون‌ها در اتم، به دور هسته می‌چرخند. هسته اتم شامل نوترون‌‌ها یا ذرات خنثی و پروتون‌ها یا ذرات با بار مثبت است. همه مواد از یک یا چند عنصر از ۱۱۸ عنصر موجود در طبیعت ساخته شده‌اند. البته عناصر ۱۱۲ تا ۱۱۸ کشف شده‌اند، اما وجود آنها تا به حال اثبات نشده است. از این ۱۱۸ عنصر، تنها ۹۲ عنصر در طبیعت یافت می‌شود. یک ماده مرکب، شامل دو یا چند عنصر است. کوچکترین واحد سازنده یک ماده مرکب،‌ «مولکول» (Molecule) نام دارد. یک یا چند اتم در کنار هم تشکیل یک مولکول می‌دهند. این اتم‌ها به وسیله نیروهای ناشی از بار الکتریکی در کنار یکدیگر نگه داشته می‌شوند.

در یک عنصر خاص، تعداد پروتون‌ها در هسته همه اتم‌های عنصر با هم برابر است. هر عنصر از شماره یک تا ۱۱۸، «عدد اتمی» (Atomic Number) خاص خود را دارد. برای یک اتم در حالت نرمال، تعداد الکترون‌ها با تعداد پروتون‌ها و عدد اتمی عنصر برابر است. الکترون‌های چرخان به دور هسته، در لایه‌های مختلف اتم قرار دارند. این الکترون‌ها، به یکدیگر نیروی دافعه و به پروتون‌های هسته اتم نیروی جاذبه وارد می‌کنند.

بیرونی‌ترین لایه یک اتم با نام «لایه ظرفیت» (Valence Shell) یا باند شناخته می‌شود. الکترون‌هایی که در لایه ظرفیت اتم قرار دارند، «الکترون‌های ظرفیت» (Valence Electrons) نام دارند. این تعریف از اتم، «مدل بور» (Bohr Model) نامیده می‌شود. خواص اتم‌ها و بارهای آن برای عناصر پرکاربرد در الکترونیک از قبیل هیدروژن، آلومینیوم، سیلیکون و ژرمانیم حائز اهمیت بسیاری است. شکل زیر، اتم تعدادی از عناصر مختلف را نشان می‌دهد:

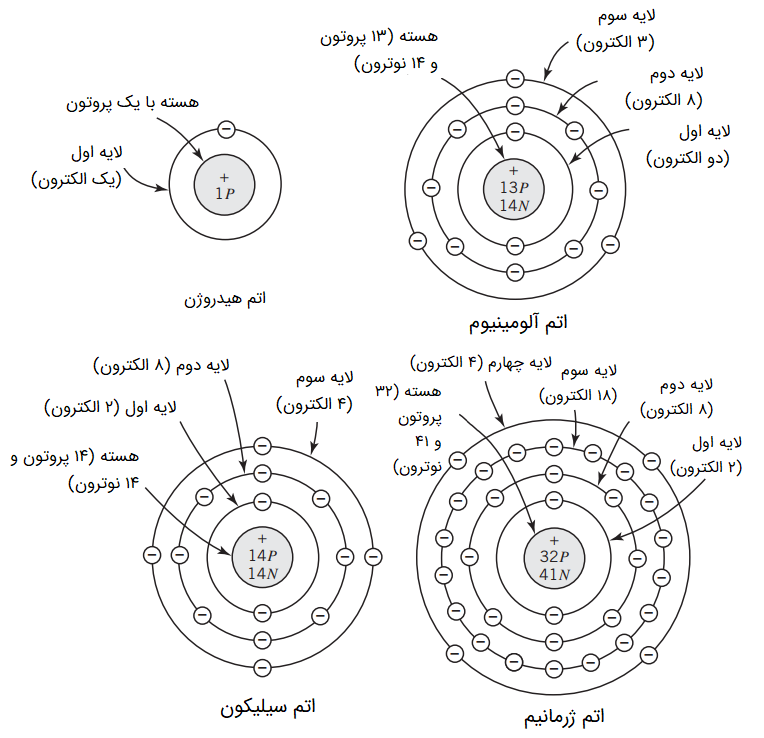
همه الکترون‌های موجود در یک لایه یا «مدار» (Orbit) از اتم، سطح انرژی یکسانی دارند. از آنجا که اطراف هسته یک اتم، لایه‌ها یا مدارهای متعددی وجود دارد، سطوح متفاوتی از انرژی نیز وجود دارد. هر کدام از این سطوح انرژی مجزا، نمایان‌گر یک لایه یا مدار با شعاع معین است. در حالت کلی، سطوح انرژی از تعداد الکترون‌ها بیشتر است. بنابراین در بعضی از سطوح انرژی (مدارها، لایه‌ها، باندهای انرژی) هیچ الکترونی وجود ندارد. مدل اتمی بور بیان می‌دارد که:

1. الکترون‌های هر اتم، فقط در حالت‌های مشخصی وجود دارند. سطح انرژی این الکترون‌ها نیز مجزاست. این سطح انرژی به شعاع مشخص آن لایه مداری وابسته است.
2. الکترون برای حرکت از لایه‌های پایین‌تر و سطوح پایین‌تر انرژی و رسیدن به لایه‌های بالاتر یا سطوح بالاتر انرژی نیاز به مقدار مشخص و ثابتی از انرژی دارد. این انرژی مشخص، «کوانتم» (Quantum) نام دارد.
3. الکترون برای حرکت از سطوح بالاتر انرژی یا لایه‌های بیرونی به سطوح پایین‌تر انرژی یا لایه‌های درونی، مقدار مشخصی انرژی را تشعشع می‌کند.
4. اگر یک الکترون سطح مشخصی از انرژی داشته باشد و در لایه یا مدار خود باقی بماند، نه انرژی جذب می‌کند و نه آن را تشعشع می‌کند.

هنگامی که یک مولکول از ترکیب یک یا چند اتم تشکیل می‌شود، نیروهای بین اتم‌های مولکول باعث ایجاد چیدمان جدیدی از بارها درون مولکول می‌شود. برای آنکه یک الکترون از اتم آزاد شود، باید انرژی لازم برای غلبه بر نیروهای اتمی و تبدیل شدن به یک بار آزاد را کسب کند.

این مسئله همانند آن است که بخواهیم یک پرتابه یا موشک را به فضا پرتاب کنیم. برای این کار باید به نیروی جاذبه یا گرانشی زمین غلبه کنیم تا پرتابه به یک جسم آزاد تبدیل شود. اما برای غلبه بر این جاذبه، به مقدار مشخصی از انرژی نیاز داریم.

دی‌الکتریک و قطبیت

«دی‌الکتریک» (Dielectric) یا «عایق» (Insulator)، ماده‌ای است که بارهای غالب در اتم‌ها و مولکول‌های آن، بارهای مثبت و منفیِ محدود هستند. این بارها به وسیله نیروهای مولکولی و اتمی در کنار یکدیگر نگه داشته شده‌اند و نمی‌توانند آزادانه حرکت کنند.

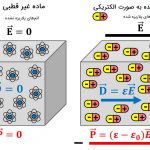
اما در یک هادی، الکترون‌ها به صورت بار آزاد وجود دارند و می‌توانند آزادانه حرکت کنند. بنابراین یک دی‌الکتریک ایده‌آل، هیچ بار آزادی ندارد و اتم‌ها و مولکول‌های آن از نظر ماکروسکوپی خنثی هستند. شکل زیر اتم یک ماده دی‌الکتریک را در غیاب میدان مغناطیسی نشان می‌دهد:

به علاوه، هنگامی که میدان خارجی به یک دی‌الکتریک اعمال می‌شود، بارهای محدودشده مثبت و منفی به سطح ماده مهاجرت نمی‌کنند. اما با اعمال میدان الکتریکی خارجی به یک هادی، بارها به دلیل آزادی، به سطح هادی مهاجرت می‌کنند. البته با اعمال میدان خارجی به دی‌الکتریک، مرکز ثقل این مواد کمی تغییر مکان می‌دهد. فرض می‌شود که این جابجایی بی‌نهایت کوچک است. به این ترتیب، تعدادی زیادی «دوقطبی الکتریکی» (‌Electric Dipole) ایجاد می‌شود. شکل زیر اتم یک ماده دی‌الکتریک را در حضور میدان مغناطیسی خارجی نشان می‌دهد:

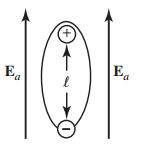
بارهای مثبت و منفی در هادی‌ها، با فاصله ماکروسکوپی از یکدیگر فاصله دارند و می‌توان آنها را از هم جدا کرد. در دی‌الکتریک‌ها، بارهای محدود امکان فاصله گرفتن از یکدیگر را ندارند و نمی‌توان آنها را از هم جدا کرد. این مسئله تفاوت اساسی بارهای محدود در دی‌الکتریک‌ها و بارهای حقیقی در هادی‌ها را نشان می‌دهد.

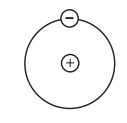
آرایش دوقطبی‌های الکتریکی در دی‌الکتریک‌ها، با نام «قطبیت جهت‌دار» (Orientational Polarization) شناخته می‌شود. شکل زیر، مفهوم یک دوقطبی الکتریکی را نشان می‌دهد:

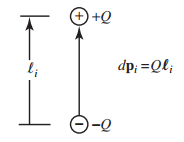
ممان دوقطبی $$dp_i$$ به وسیله رابطه زیر تعریف می‌شود:

$$\Large dp_i = Q l_i$$
معادله (۱)

در این معادله، $$Q$$ (با واحد کولن) مقدار هریک از بارهای مثبت و منفی است که به اندازه $$l_i$$ از یکدیگر فاصله دارند.

هنگامی که به یک ماده، میدان الکتریکی اعمال می‌شود، دوقطبی‌های قطبیت ماده با میدان الکترومغناطیسی اعمال‌شده تعامل خواهند داشت. صرفنظر از اینکه دی‌الکتریک جامد، مایع یا گاز باشد، این تعامل باعث می‌شود که ماده بتواند انرژی الکتریکی در خود ذخیره کند. ذخیره‌سازی انرژی به دلیل جابجایی مرکز ثقل ماده روی می‌دهد. این مسئله همانند بلند کردن یک وزنه یا فشرده کردن یک فنر است و «انرژی پتانسیل» (Potential Energy) را نشان می‌دهد.

حضور این دوقطبی‌ها را می‌توان به مدل میکروسکوپی ماده مربوط دانست. در این مدل، ممان هر یک از بارها و دوقطبی‌ها به وسیله معادله (۱) مشخص می‌شود. اگرچه این فرآیند بسیار دقیق است، اما بسیار غیر عملی است. برای مثال در یک تیغه دی‌الکتریک، محاسبه ممان دوقطبی‌ها کاری بسیار زمان‌بر است، زیرا مکان فضایی هر یک از اتم‌ها و مولکول‌های ماده باید دانسته شود. در عمل به جای این کار، رفتار دوقطبی‌ها و بارهای محدود به وسیله یک روش کیفی پیش‌بینی می‌شود. در این روش، یک «بردار قطبیت الکتریکی» (Electric Polarization Vector) یا P با استفاده از مدل ماکروسکوپی تعریف می‌شود که شامل هزاران اتم و مولکول است.

ممان دوقطبی کلی یک ماده ($$p_t$$)، به صورت جمع ممان‌های دوقطبی در همه دوقطبی‌ها با قطبیت جهت‌دار تعریف می‌شود. ممان هر یک از این دو قطبی‌ها به وسیله رابطه (۱) داده می‌شود. برای یک حجم $$\Delta v$$ که به اندازه $$N_e$$ دوقطبی الکتریکی در واحد حجم یا به طور کلی $$N_e \Delta v$$ دوقطبی الکتریکی دارد، می‌توان نوشت:

$$\Large p_t = \sum_{i=1}^{N_e \Delta v}dp_i$$
معادله (۲)

بردار پلاریزاسیون الکتریکی ($$P$$) را می‌توان به صورت ممان دوقطبی در واحد حجم تعریف کرد. یعنی:

$$\Large P= \lim_{\Delta v\to 0} \left[ \frac{1}{\Delta v} p_t\right]=\lim_{\Delta v \to 0}\left [ \frac{1}{\Delta v} \sum_{i=1}^{N_e \Delta v}dp_i \right ] (C/m^2)$$
معادله (۳)

بردار $$P$$ چگالی بار سطحی را نشان می‌دهد و واحد آن کولن بر متر مکعب یا کولن بر متر مربع است. ذکر این نکته ضروری است که $$P$$ چگالی بار سطحی محدود ($$q_{sp}$$) است و نمی‌توان بارهای مثبت و منفی را از یکدیگر جدا کرد. بنابراین در یک حجم، تعداد مشخصی جفت بار مثبت و منفی (دوقطبی) وجود دارد و بار خالص ماده باید صفر باشد. بنابراین نمی‌توان از این بار سطحی محدود در شرایط مرزی الکترومغناطیسی برای محاسبه میدان‌های الکتریکی و مغناطیسی استفاده کرد.

ممان دوقطبی متوسط هر مولکول به صورت زیر فرض می‌شود:

$$\Large dp_i = dp_{av}= Q l_{av}$$
معادله (۴)

اگر همه دوقطبی‌ها در یک جهت مشخص به موازات هم قرار گیرند، بردار پلاریزاسیون الکتریکی با استفاده از معادله (۳) قابل محاسبه است:

$$P=\Large \lim _{\Delta v \to 0} \left[ \frac{1}{\Delta v}\sum_{ i=1}^{N_e \Delta v} dp_i\right] = N_e dp_{av}= N_e Q l_{av}$$
معادله (۵)

مکانیزم تولید قطبیت الکتریکی برای دی‌الکتریک‌ها به یکی از سه روش زیر است. البته قطبیت الکتریکی در برخی مواد، می‌تواند به هر سه روش تولید شود.

1. قطبیت جهت‌دار یا دوقطبی: این قطبیت در غیاب میدان‌های الکتریکی خارجی وجود دارد و مربوط به مشخصات ساختار ماده است. قطبیت جهت‌دار، ناشی از ممان‌های دوقطبی دائمی داخل خود ماده است که جهت‌گیری تصادفی دارند. هرچند هنگامی که یک میدان الکتریکی خارجی اعمال می‌شود، دوقطبی‌ها تمایل دارند که با میدان اعمالی هم‌جهت شوند. به این مواد، «قطبی» (Polar) گویند. یک مثال از این نوع مواد، آب است.
2. قطبیت مولکولی یا یونی: این پلاریزاسیون در موادی مثل سدیم کلراید (NaCl) یا همان نمک خوراکی مشاهده می‌شود. اتم‌ها در این پلاریزاسیون، یون‌های مثبت و منفی دارند و هنگامی که میدان الکتریکی به آنها اعمال می‌شود، جابجا می‌شوند.
3. قطبیت الکترونیکی: این قطبیت در بیشتر مواد وجود دارد. هنگامی که یک میدان الکتریکی به ماده اعمال می‌شود، مرکز ابر الکتریکی اتم نسبت به مرکز هسته جابجا می‌شود. به این ترتیب، دوقطبی‌های الکتریکی به وجود می‌آید.

شکل زیر، مکانیزم‌های مختلف تولید قطبیت الکتریکی در دی‌الکتریک‌ها را نشان می‌دهد:

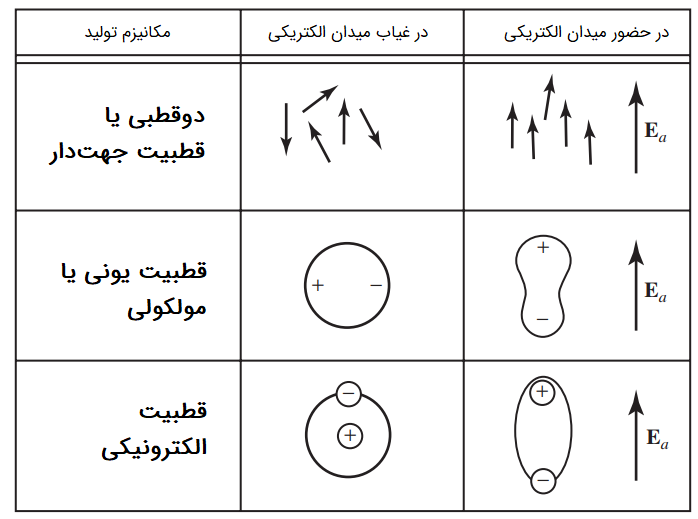
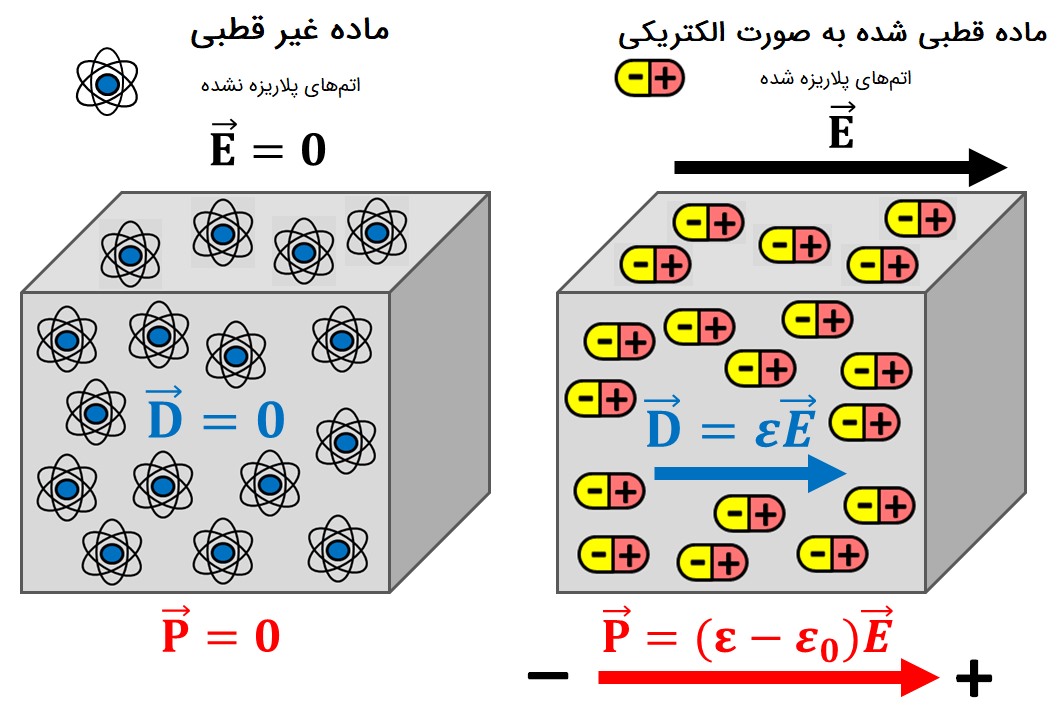
اگر بارهای موجود در یک ماده در غیاب میدان الکتریکی خارجی $$E_a$$ به گونه‌ای متوسط‌گیری شوند که بارهای مثبت و منفی در کل ماده یکدیگر را خنثی کنند، آنگاه دوقطبی شکل نمی‌گیرد و ممان دوقطبی کلی در معادله (۲) و بردار قطبیت الکتریکی $$P$$ در معادله (۳) برابر صفر می‌شوند. هرچند اگر یک میدان الکتریکی خارجی اعمال شود، قطبیت دیگر صفر نخواهد بود. به چنین ماده‌ای، «غیر قطبی» (Nonpolar) گویند. شکل زیر دو نوع مختلف ماده را نشان می‌دهد:

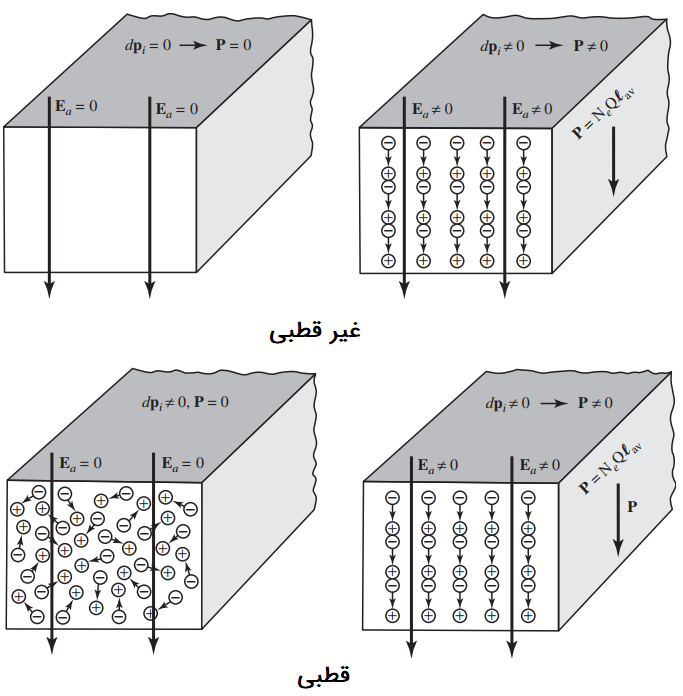
در مواد قطبی بدون آنکه میدان الکتریکی خارجی اعمال شود، تعدادی دوقطبی مشخص وجود دارد. ممان دوقطبی $$p_i$$ برای هر یک از این دوقطبی‌ها طبق معادله (۱) محاسبه می‌شود. اما ممان دوقطبی خالص آن ($$p_t$$) برابر صفر خواهد بود. جهت‌گیری این دوقطبی‌ها تصادفی است. به همین دلیل، ممان دوقطبی کل ($$p_t$$) و بردار قطبیت الکتریکی ($$P$$) برابر صفر هستند. این پدیده، معمولا نتیجه جهت‌گیری تصادفی دوقطبی‌هاست که در شکل (۶) نشان داده شده است. مقدار ممان دوقطبی برای مواد قطبی معمولا در حدود $$10^{-30}C\cdot m$$ است. موادی که در غیاب میدان الکتریکی خارجی $$E_a$$، ممان دوقطبی و بردار پلاریزاسیون الکتریکی ($$P$$) غیر صفر دارند، به نام «الکتریت» (Electret) شناخته می‌شوند.

یک گروه دیگر از مواد دی‌الکتریک، «فروالکتریک» (Ferroelectric) است. در این مواد، منحنی قطبیت ($$P$$) نسبت به میدان الکتریکی ($$E$$) یک «حلقه هیسترزیس» (Hysteresis Loop) تشکیل می‌دهد. این حلقه همانند حلقه هیسترزیس تشکیل‌شده در منحنی چگالی شار مغناطیسی ($$B$$) نسبت به میدان مغناطیسی ($$H$$) در مواد فرومغناطیس است. منحنی $$P$$ نسبت به $$E$$ در مواد فروالکتریک، یک «قطبیت باقیمانده» (Remnant Polarization) به اندازه $$P_r$$ و یک «میدان وادارنده الکتریکی» (Coercive Electric Field) دارد که با نماد $$E_r$$ نشان داده می‌شود.

در یک دمای بحرانی که به آن «دمای کوری فروالکتریک» (Ferroelectric Curie Temperature) گفته می‌شود، قطبیت خودبخودی در فروالکتریک از بین می‌رود. بالاتر از دمای کوری «گذردهی الکتریکی نسبی» (Relative Permitivity)، بر اساس «قانون کوری-وایس» (Curie-Weiss Law) تغییر می‌کند. پایین‌تر از این دما، چگالی شار الکتریکی $$D$$ و قطبیت $$P$$ توابعی خطی از میدان الکتریکی $$E$$ نیستند. به عنوان یک مثال از مواد فروالکتریک می‌توان باریم تیتانات ($$BaTiO_3$$) را نام برد.

بار دیگر شکل (۶) را در نظر بگیرید. هنگامی که یک میدان الکتریکی به ماده دی‌الکتریکی قطبی یا غیر قطبی اعمال می‌شود، بارها در دو محیط جهت‌گیری مشخصی پیدا می‌کنند. به این ترتیب دوقطبی‌ها، یک ممان دوقطبی غیر صفر را در داخل ماده تشکیل می‌دهند. هرچند، هنگامی که این ماده در ابعاد میکروسکوپی بررسی می‌شود، موارد زیر از شکل (۶) بدیهی خواهند بود:

1. در سطح پایینی، چگالی سطحی خالص بار مثبت محدود به اندازه $$q_s^+$$ خواهد بود.
2. در سطح بالایی، چگالی سطحی خالص بار منفی محدود به اندازه $$q_s^-$$ خواهد بود.
3. چگالی بار حجمی $$q_v$$ داخل ماده برابر صفر خواهد بود. زیرا بارهای مثبت و منفی در دوقطبی‌های مجاور، اثر یکدیگر را خنثی خواهند کرد.

مواردی که در بالا بیان شدند، به صورت ماکروسکوپی نیز قابل مشاهده هستند. شکل زیر را در نظر بگیرید:

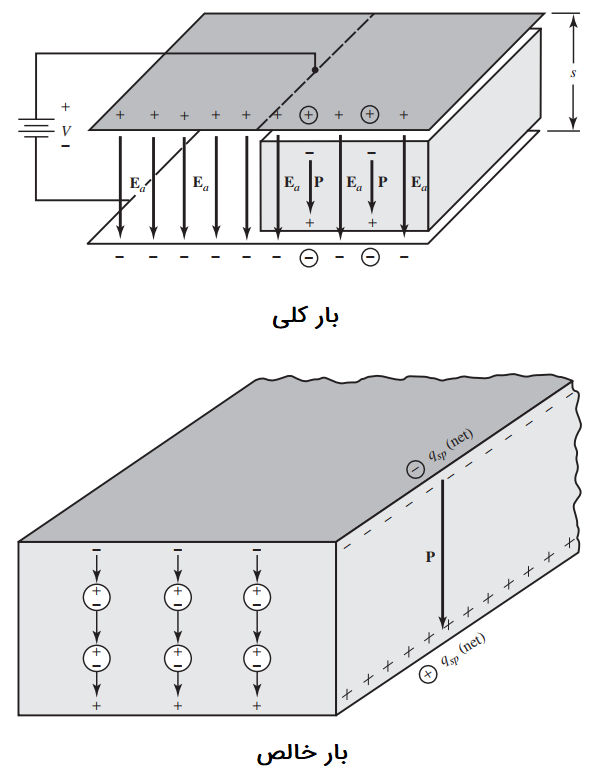
یک منبع ولتاژ DC به دو صفحه فلزی با فاصله $$s$$ وصل می‌شود. در این حالت، نصف فضای بین دو صفحه موازی به وسیله دی‌الکتریک اشغال می‌شود و نیمه دیگر، فضای آزاد است. فرض کنید در نیمه فضای آزاد، پنج بار آزاد روی هر کدام از صفحات حضور داشته باشد. به همین تعداد بار آزاد نیز روی صفحات در ناحیه دی‌الکتریک وجود دارد. به دلیل چینش مجدد بارهای محدود در ماده دی‌الکتریک و شکل‌گیری دوقطبی‌های الکتریکی و خنثی شدن اثر بارهای مخالف هم در شکل (۷)، بردار قطبیت الکتریکی $$P$$ داخل ماده دی‌الکتریک شکل می‌گیرد. بنابراین بردار قطبیت $$P$$ در نتیجه چگالی سطحی بار محدود $$-q_{sp}$$ در سطح بالایی و چگالی سطحی بار محدود $$+q_{sp}$$ در سطح پایینی تیغه دی‌الکتریک ایجاد می‌شود.

فرض کنید که دو جفت بار محدود که چگالی سطحی بار محدود $$q_{sp}$$ را شکل می‌دهند، روی سطح تیغه دی‌الکتریک شکل (۷) موجود باشند. بار الکتریکی منفی روی سطح بالایی و بار الکتریکی مثبت روی سطح پایینی این تیغه قرار دارد. سطح تیغه در تماس با صفحه‌های خازن فرض شده است. به همین دلیل دو بار منفی محدود روی سطح بالایی دی‌الکتریک، دو بار مثبت آزاد روی سطح بالایی خازن را خنثی می‌کند. همین پدیده در صفحه پایینی نیز روی می‌دهد. به این ترتیب تعداد خالص بارها روی صفحه‌های بالایی و پایینی صفحه خازنی به سه عدد کاهش می‌یابد و شدت میدان الکتریکی در ماده دی‌الکتریک بین دو صفحه خازنی کاهش می‌یابد.

به دلیل منبع ولتاژ DC ثابت بین دو صفحه خازنی و بارهای آزاد اضافی روی هر کدام از این دو صفحه (بار مثبت روی صفحه بالایی و بار منفی روی صفحه پایینی) کل بار خالص روی صفحات بالایی و پایینی خازن و شدت میدان الکتریکی در ماده دی‌الکتریک بین دو صفحه ثابت باقی می‌ماند. در شکل (۷) دو بار آزاد القا شده با علامت دایره مشخص شده‌اند.

گذردهی الکتریکی

در همه وضعیت‌های پیشین، اثر خالص بین صفحه‌های بالایی و پایینی دی‌الکتریک در نظر گرفته شده است. یک بردار قطبیت الکتریکی خالص با نام $$P$$ تعریف کردیم و جهت این بردار را از صفحه بالایی به سمت صفحه پایینی رسم کردیم. این بردار هم‌جهت با میدان الکتریکی اعمالی $$E_a$$ است. اندازه این بردار با رابطه زیر مشخص می‌شود:

$$\Large P = q_{sp}$$
معادله (۶)

در این معادله میدان الکتریکی اعمالی $$E_a$$ مقداری ثابت دارد. اما چگالی شار الکتریکی داخل ماده دی‌الکتریک با حالتی که به جای دی‌الکتریک فضای آزاد قرار دارد، متفاوت است. در شکل (۷)، قسمتی از خازن که با فضای آزاد اشغال شده است، چگالی شار الکتریکی $$D_0$$ به وسیله رابطه زیر داده می‌شود:

$$\Large D_0 = \varepsilon_0 E_a$$
معادله (۷)

در قسمت دی‌الکتریک بین دو صفحه خازنی، چگالی شار الکتریکی $$D$$ با چگالی شار الکتریکی $$D_0$$ در فضای آزاد به صورت زیر رابطه دارد:

$$\Large D= \varepsilon_0 E_a + P$$
معادله (8)

اندازه بردار $$P$$ با معادله (۶) مشخص می‌شود. چگالی شار الکتریکی $$D$$ در معادله (۸) را می‌توان به شدت میدان الکتریکی اعمالی $$E_a$$ نیز مربوط دانست. پارامتری به نام $$\varepsilon_s$$ را برای ارتباط بین $$D$$ و $$E_a$$ با واحد فاراد بر متر تعریف می‌کنیم. بنابراین می‌توان نوشت:

$$\Large D= \varepsilon_s E_a$$
معادله (۹)

با مقایسه روابط (۸) و (۹) می‌توان $$P$$ را بر $$E_a$$ نوشت. داریم:

$$\Large P=\varepsilon_0\chi _e E_a$$
معادله (10)

یا به عبارت دیگر:

$$\Large \chi _e = \frac{1}{\varepsilon_0} \frac{P}{E_a}$$
معادله (۱۱)

 $$\chi_e$$ در معادله (۱۱)، «حساسیت الکتریکی» (Electric Susceptibility) نام دارد و بدون واحد است.

با جایگزینی معادله (10) در معادله (8) و قرار دادن آن در معادله (۹) خواهیم داشت:

$$\Large D= \varepsilon_0 E_a + \varepsilon_0 \chi_e E_a = \varepsilon_ 0 (1+ \chi_e)E_a =\varepsilon_s E_a$$
معادله (۱۲)

یا به عبارت دیگر:

$$\Large \varepsilon_s = \varepsilon_ 0 (1+ \chi_e)$$
معادله (۱۳)

در معادله (۱۳)، $$\varepsilon_s$$ «ضریب گذردهی الکتریکی استاتیک» (Static Perimitvity) برای محیط نام دارد. مقدار ضریب گذردهی الکتریکی نسبی برابر $$\varepsilon_{sr}$$ نسبت به گذردهی الکتریکی فضای آزاد ($$\varepsilon_0$$) فرض می‌شود. این ضریب به صورت زیر تعریف می‌شود:

$$\Large \varepsilon_{sr}= \frac{\varepsilon_s}{\varepsilon_0} = 1+ \chi_e$$
معادله (14)

که معمولا به آن «گذردهی الکتریکی نسبی» (Relative Permitvity) گفته می‌شود. این ضریب در عمل، «ثابت دی‌الکتریک» (Dielectric Constant) نام دارد. مهندسان و دانشمندان، گذردهی الکتریکی را به گونه‌ای انتخاب می‌کنند که ریشه دوم آن با «ضریب شکست» (Index of Refraction) برابر شود.

بنابراین ثابت دی‌الکتریک یک ماده دی‌الکتریک، قابلیت ذخیره سازی نسبی بار الکتریکی (نسبت به فضای آزاد) یا انرژی را در ماده دی‌الکتریک نشان می‌دهد. هرچه مقدار این ثابت بزرگتر باشد، قابلیت ذخیره بار یا انرژی نیز بیشتر خواهد بود. خازن‌های صفحه موازی از ماده دی‌الکتریک بین صفحات خود استفاده می‌کنند تا ظرفیت ذخیره بار یا انرژی در آنها افزایش یابد. در این حالت، بارهای آزاد بیشتری روی صفحه خازن القا می‌شوند. این بارهای آزاد، اثر بارهای محدود روی سطح دی‌الکتریک را خنثی می‌کنند. به همین دلیل، شدت میدان الکتریکی و پتانسیل بین دو صفحه خازن ثابت باقی می‌ماند.

مثال

ثابت دی‌الکتریک استاتیک آب مقداری برابر ۸۱ دارد. فرض کنید شدت میدان الکتریکی اعمالی به آب، برابر $$1V/m$$ باشد. مقدار چگالی شار الکتریکی و بردار قطبیت الکتریکی داخل آب را بیابید.

حل: با استفاده از معادله (۹) خواهیم داشت:

$$\large D= \varepsilon_s E_a = 81(8.854 \times 10^{-12})(1) = 7.17 \times 10^{-10}\text{C/m^2}$$

با استفاده از معادله (14) نیز خواهیم داشت:

$$\large \chi_e = \varepsilon_{sr}-1 = 81-1 =80$$

بنابراین اندازه بردار قطبیت الکتریکی با استفاده از معادله (۱۰) به صورت زیر به دست می‌آید:

$$\large P= \varepsilon_0 \chi_e E_a =8.854 \times 10^{-12} (80)(1)=7.08 \times 10^{-10} \text{C/m^2}$$

ضریب گذردهی الکتریکی در معادله (12) یا فرم نسبی آن در معادله (14)، در فرکانس‌های ساکن یا شبه ساکن معتبر است. اگر میدان‌های الکترومغناطیسی متغیر با فرکانس داشته باشیم، گذردهی الکتریکی تابعی از فرکانس متغیر میدان خواهد بود.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• امواج الکترومغناطیسی — از صفر تا صد
• میدان مغناطیسی جریان — از صفر تا صد

^^