چرخه کارنو — به زبان ساده

در اوایل قرن نوزدهم میلادی، موتورهای بخار نقش مهمی در صنعت و حمل و نقل پیدا کردند. در سال 1824، «نیکولاس لئونارد سعدی کارنو» (Nicolas Léonard Sadi Carnot)، مهندس فرانسوی، کتابی تحت عنوان «اندیشه‌هایی درباره نیروی محرکه گرما» منتشر کرد. او در این کتاب، نظریه‌ای پیرامون موتورهای حرارتی و همچنین مدل ایده‌آلی برای یک موتور حرارتی ارائه کرد. این نظریه، امروزه به عنوان چرخه کارنو (Carnot Cycle) شناخته می‌شود. توسعه قانون دوم ترمودینامیک توسط کارنو موجب شد تا از او به عنوان پدر علم ترمودینامیک یاد شود. در این مقاله، ابتدا به معرفی چرخه کارنو می‌پردازیم. سپس کار و تبادل گرما را در آن محاسبه می‌کنیم. در پایان نیز راندمان این چرخه را به دست خواهیم آورد.

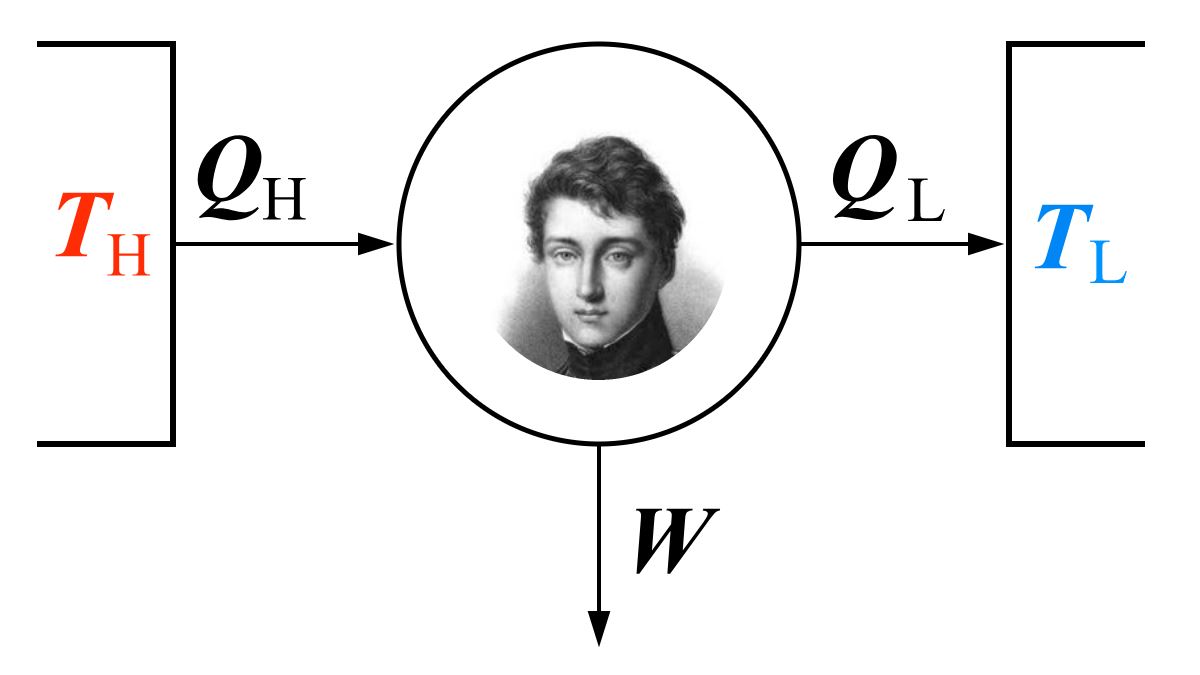
مراحل چرخه کارنو

چرخه کارنو از چهار فرآیند برگشت‌پذیر تشکیل شده است. شماتیک این چهار مرحله را در شکل زیر مشاهده می‌کنید.

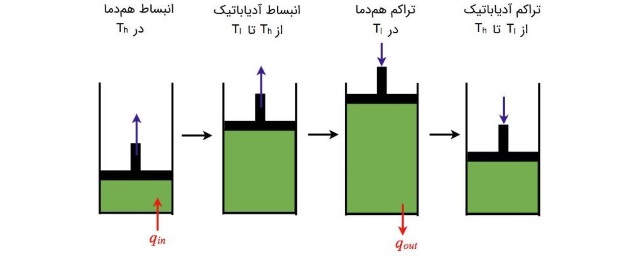
• فرآیند انبساط هم‌دما: در این فرآیند، گاز ایده‌آل، گرمای $$q_{in}$$ را از یک منبع گرما با دمای $$T_h$$ دریافت می‌کند. در این حین، گاز منبسط شده و روی محیط، کار انجام می‌دهد.

فیلم آموزش فیزیک پایه دهم – فیزیک 1 در فرادرس

کلیک کنید

• فرآیند انبساط آدیاباتیک: در مرحله دوم، انتقال حرارت سیستم با محیط صفر است. گاز منبسط می‌شود و روی محیط، کار انجام می‌دهد. در نتیجه دمای سیستم تا $$T_l$$ پایین می‌آید.
• فرآیند تراکم هم‌دما: در این مرحله، محیط روی گاز کار انجام می‌دهد و دمای $$T_l$$ ثابت می‌ماند. به همین دلیل، گاز گرمای $$q_{out}$$ را از دست می‌دهد.
• فرآیند تراکم آدیاباتیک: بالاخره در مرحله چهارم و در شرایطی که انتقال گرما با محیط صفر است، محیط روی گاز کار انجام می‌دهد. در انتهای این فرآیند، دمای گاز تا $$T_h$$ بالا می‌رود.

نمودار P-V

برای تحلیل این چرخه، نمودار فشار برحسب حجم را که در پایین رسم شده است، در نظر بگیرید. در فرآیندهای اول و سوم که هم‌دما هستند، $$\large \Delta U=0$$ است. زیرا در این فرآیندها، دما تغییر نمی‌کند. فرآیندهای دوم و چهارم آدیاباتیک (بی‌دررو) هستند و انتقال گرما صفر است. مقادیر کار، انتقال گرما، $$\large \Delta U$$ و $$\large \Delta H$$ را می‌توان در هریک از این مراحل به صورت زیر محاسبه کرد.

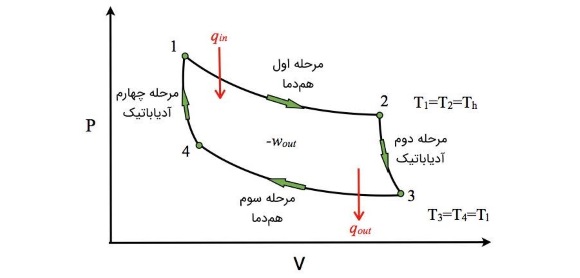
در فرآیند انبساط هم‌دما که در مرحله اول رخ می‌دهد، مقدار $$\large \Delta U$$ و $$\large \Delta H$$ صفر است و فقط انتقال کار و گرما داریم.

$$\large W_{1\rightarrow2} =-nRT_h\ln(\frac{V_2}{V_1})\\~\\ \large Q_{1\rightarrow2} = nRT_h\ln(\frac{V_2}{V_1})$$

در فرآیند انبساط آدیاباتیک که در مرحله دوم رخ می‌دهد، تبادل گرما با محیط صفر است. ولی سایر مقادیر به صورت زیر قابل محاسبه است.

$$\large W_{2\rightarrow3} =n\bar{C}_v(T_l-T_h)\\~\\ \large \Delta U_{2\rightarrow3} = n\bar{C}_v(T_l-T_h)\\~\\ \large \Delta H_{2\rightarrow3}=n\bar{C}_p(T_l-T_h)$$

در فرآیند تراکم هم‌دما که در مرحله سوم رخ می‌دهد، دما ثابت است. در نتیجه، مقدار $$\large \Delta U$$ و $$\large \Delta H$$ صفر است و فقط تبادل کار و گرما انجام می‌شود.

$$\large W_{3\rightarrow4} =-nRT_h\ln(\frac{V_4}{V_3})\\~\\ \large Q_{3\rightarrow4} = nRT_h\ln(\frac{V_4}{V_3})$$

در مرحله آخر، فرآیند تراکم آدیاباتیک رخ می‌دهد. در این فرآیند، تبادل گرما با محیط صفر است. در نتیجه مقدار $$\large \Delta U$$ با مقدار کار انجام شده برابر است. برای محاسبه این مقادیر و همچنین به دست آوردن $$\large \Delta H$$ به صورت زیر عمل می‌کنیم.

$$\large W_{4\rightarrow1} =n\bar{C}_v(T_h-T_l)\\~\\ \large \Delta U_{4\rightarrow1} = n\bar{C}_v(T_h-T_l)\\~\\ \large \Delta H_{4\rightarrow1}=n\bar{C}_p(T_h-T_l)$$

نمودار T-S

نمودار دما برحسب آنتروپی در چرخه کارنو، به صورت زیر است.

فیلم آموزش ترمودینامیک مهندسی شیمی ۲ – مرور و حل مساله در فرادرس

کلیک کنید

مقادیر $$\large \Delta T$$ و $$\large \Delta S$$ را می‌توان در هریک از این چهار مرحله به صورت زیر به دست آورد.

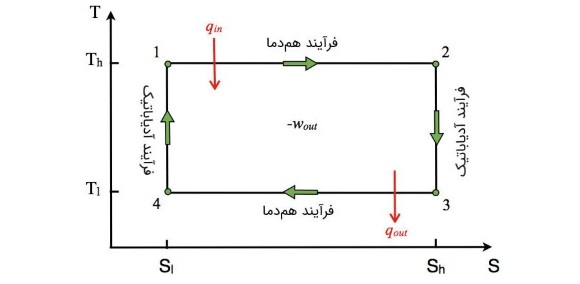
در فرآیند انبساط هم‌دما که در مرحله اول رخ می‌دهد، مقدار $$\large \Delta T$$ صفر است. برای محاسبه تغییر آنتروپی می‌توان از رابطه زیر استفاده کرد.

$$\large \Delta S_{1\rightarrow2} =-nR\ln(\frac{V_2}{V_1})$$

در فرآیند انبساط آدیاباتیک که در مرحله دوم رخ می‌دهد، با توجه به تعریف فرآیند آدیاباتیک، تغییر آنتروپی صفر است. در این حالت، فقط تغییر دما رخ داده، که آن هم برابر با $$\large T_l-T_h$$ است.

در مرحله سوم، فرآیند تراکم به صورت هم‌دما رخ داده است. در نتیجه دمای ابتدا و انتهای فرآیند با هم برابرند. تغییر آنتروپی از نقطه ۳ به ۴ با کمک رابطه زیر به دست می‌آید.

$$\large \Delta S_{3\rightarrow4} =-nR\ln(\frac{V_4}{V_3})$$

فرآیند انبساطی که در مرحله چهارم اتفاق افتاده، از نوع آدیاباتیک یا بی‌دررو است. در نتیجه آنتروپی از نقطه ۴ به ۱ بدون تغییر می‌ماند. تغییر دما در این فرآیند برابر $$\large T_h-T_l$$ است.

راندمان چرخه کارنو

راندمان چرخه کارنو به صورت نسبت انرژی خروجی به انرژی ورودی تعریف شده و به صورت زیر نشان داده می‌شود. این چرخه در بین تمام چرخه‌های موتور حرارتی که بین دو دمای $$\large T_h$$ و $$\large T_l$$ کار می‌کنند، بیشترین بازده را به همراه دارد. دقت کنید که دما باید برحسب کلوین محاسبه شود.

$$\large \eta =\frac{-W_{net}}{Q_h}=\frac{nRT_h\ln(\frac{V_2}{V_1})+nRT_l\ln(\frac{V_4}{V_3})}{nRT_h\ln(\frac{V_2}{V_1})}$$

فرآیندهای دوم و چهارم آدیاباتیک هستند. در نتیجه رابطه‌های زیر برقرار است.

$$\large (\frac{T_2}{T_3})^{C_V/R}=\frac{V_3}{V_2},~~~~~~~~ \large (\frac{T_1}{T_4})^{C_V/R}=\frac{V_4}{V_1}$$

از طرفی هم مراحل اول و سوم هم‌دما هستند. پس رابطه‌های زیر را می‌توان نوشت.

$$\large \frac{V_3}{V_4}=\frac{V_2}{V_1}$$

با ادغام تمام این رابطه‌ها، راندمان چرخه کارنو به صورت زیر به دست می‌آید.

$$\large \eta =1-\frac{Q_l}{Q_h}=1-\frac{T_l}{T_h}$$

مثال

سؤال: در یک نیروگاه حرارتی دمای بویلر $$550\:K$$ و دمای اگزوز خروجی برابر $$400\:K$$ است. اگر عملکرد این نیروگاه مطابق چرخه کارنو باشد، با فرض توان خروجی $$2.5\:MW$$، انرژی حرارتی جذب و دفع شده را در هر ثانیه محاسبه کنید.

پاسخ: ابتدا راندمان چرخه کارنو را به دست می‌آوریم.

$$\large \eta =1-\frac{T_l}{T_h} =1-\frac{400}{550}=0.273$$

حال با داشتن راندمان چرخه کارنو و توان خروجی، مقادیر انرژی حرارتی به راحتی محاسبه می‌شود.

$$\large \eta =\frac{-W_{net}}{Q_h} \Rightarrow 0.273=\frac{-2.5\:MJ}{Q_h}\\~\\ \large \Rightarrow Q_h=9.2\:MJ\\~\\ \large \Delta U=Q+W=Q_h+Q_l+W=0\\~\\ \large \Rightarrow Q_l=-6.7\:MJ$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک حرارت و سیالات،‌ آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• آنتروپی — از صفر تا صد
• فرآیند آدیاباتیک — به زبان ساده
• سیکل ترمودینامیکی اتو (Otto Cycle) و موتور احتراق داخلی — یادگیری با مثال
• سیکل ترمودینامیکی چیست؟ — به زبان ساده

^^