چرخ دنده ساده و محاسبات آن – از صفر تا صد

قبلاً در مجله فرادرس، انواع پرکاربرد چرخ دنده را در مقاله چرخ دنده - به زبان ساده معرفی کردیم. ساده‌ترین نوع آنها چرخ دنده ساده بود. چرخ دنده ساده برای انتقال نیرو بین محورهای موازی به کار می‌رود. این نوع چرخ دنده، به دلیل شکل ظاهری در دسته چرخ دنده‌های استوانه‌ای قرار می‌گیرد. سطح دندانه‌ها در این چرخ دنده، موازی محور است. در نتیجه، هیچ‌گونه نیروی تراستی در جهت محور ایجاد نخواهد شد. به دلیل ساختار ساده، چرخ دنده ساده را می‌توان با بیشترین دقت ممکن ساخت. راندمان چرخ دنده ساده در بازه $$94$$ تا $$98$$ درصد تغییر می‌کند. یکی از مهمترین معایب این چرخ دنده‌ها، سر و صدای آنهاست. هنگامی که دو چرخ دنده ساده با یکدیگر درگیر می‌شوند، با برخورد دندانه‌ها به یکدیگر، نویز و تمرکز تنش زیادی ایجاد می‌شود. پیش از محاسبه سرعت و نیروهای وارد به چرخ دنده ساده لازم است برخی اصطلاحات مربوط به هندسه چرخ دنده را تعریف کنیم.

پارامترهای هندسی چرخ دنده ساده

تصویر زیر، یک چرخ دنده ساده را از نزدیک نشان داده است. پارامترهای اصلی چرخ دنده را در شکل می‌بینید. در ادامه به تعریف برخی از این پارامترها خواهیم پرداخت.

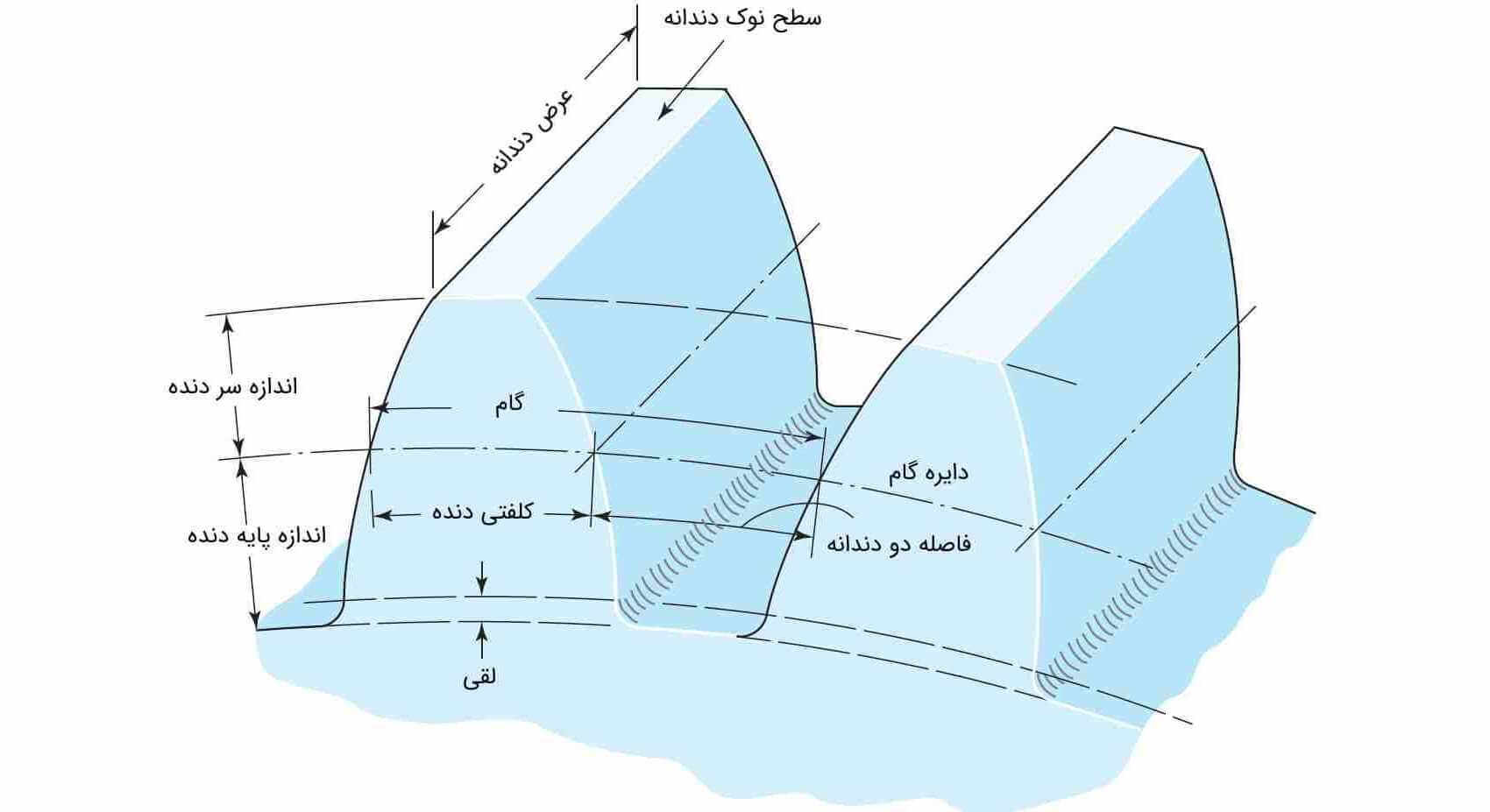
• گام: فاصله یک نقطه‌ روی دندانه تا نقطه متناظرش در دندانه مجاور بعدی را گام (Pitch) چرخ دنده می‌نامند. این فاصله با $$p$$ نشان داده می‌شود. مجموع کلفتی دنده و فاصله دو دندانه مجاور برابر با گام است.
• اندازه سر دنده: به فاصله شعاعی بین بالای دندانه تا دایره گام، سر دنده (Addendum) گفته می‌شود و آن را با $$a$$ نشان می‌دهند.
• اندازه پایه دنده: به فاصله شعاعی از ریشه دندانه تا دایره گام، اندازه پایه دنده (Dedendum) گفته می‌شود و آن را با $$d$$ نشان می‌دهند.
• عمق دندانه: به مجموع اندازه سر دنده و پایه دنده، عمق دندانه گفته می‌شود.

شکل زیر، دو چرخ دنده درگیر را نشان می‌دهد. برخی دیگر از پارامترهای اصلی در این شکل نشان داده شده است. آنها را با هم مرور می‌کنیم.

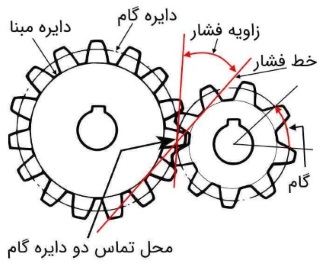
• دایره مبنا: دایره مبنا (Base Circle) دایره‌ای است که دندانه‌ها روی آن قرار گرفته‌اند.
• دایره گام: هنگامی که دو چرخ دنده باهم درگیر می‌شوند، دو دایره فرضی وجود دارد که به هم مماس هستند. این دو دایره، دایره گام (Pitch Circle) و قطر آنها نیز، قطر گام (Pitch Diameter) نامیده می‌شوند. برای به دست آوردن گام، محیط دایره گام را به تعداد دندانه‌ها تقسیم می‌کنیم.
• خط فشار: خطی که به هر دو دایره مبنا مماس است، خط فشار نامیده می‌شود. زاویه بین خط فشار و خط تماس دایره‌های گام، به عنوان زاویه فشار شناخته می‌شود. در طراحی‌ها، زاویه فشار معمولاً $$14.5$$، $$20$$ و $$25$$ درجه در نظر گرفته می‌شود.
• مدول چرخ دنده: یکی از مهمترین مشخصه‌های هر چرخ دنده که معیاری از سایز آن چرخ دنده را بیان می‌کند، مدول (Module) چرخ دنده نامیده می‌شود. مدول چرخ دنده به صورت نسبت قطر دایره گام (برحسب میلی‌متر) به تعداد دندانه‌ها و به صورت زیر تعریف می‌شود. مدول چرخ دنده را همچنین می‌توان با تقسیم گام به عدد $$\large \pi$$ محاسبه کرد. این مشخصه، عموماً عددی بین $$0.3$$ تا $$25$$ میلی‌متر است. مدول چرخ دنده با اندازه سر دنده برابر است. در بیشتر موارد، اندازه پایه دنده نیز با حاصل‌ضرب عدد $$1.25$$ در مدول چرخ دنده برابری می‌کند. شرط اینکه دو چرخ دنده با هم درگیر شوند، این است که مدول یکسان داشته باشند.
• گام قطری: گام قطری با $$P$$ (حرف بزرگ) نشان داده شده و عکس مدول محاسبه می‌شود. تعداد دندانه‌ها تقسیم بر قطر دایره گام، برابر با گام قطری (Diametral Pitch) است. گام ($$p$$) و گام قطری ($$P$$) دو مفهوم مجزا هستند و با رابطه $$\large p=\frac{\pi}{P}$$ می‌توان یکی را برحسب دیگری محاسبه کرد.

محاسبه سرعت در چرخ دنده ساده

هنگامی که دو چرخ دنده باهم درگیر می‌شوند، دایره‌های گام آنها بدون لغزش روی هم می‌غلتند. بنا به قرار داد، در نام‌گذاری‌ها عدد ۱ به قاب و چهارچوب ماشین اختصاص داده می‌شود. پس از آن، چرخ دنده‌ها با شروع از عدد ۲ نام‌گذاری می‌شوند. شعاع دایره گام هریک از دو چرخ دنده را $$r_2$$ و $$r_3$$ می‌نامیم. هر دو دایره به ترتیب با سرعت زاویه‌ای $$\omega_2$$ و $$\omega_3$$ در حال چرخش هستند. در این وضعیت، سرعت خطی ذره‌ای که روی دایره گام قرار دارد، به صورت زیر محاسبه می‌شود.

$$\large V=|r_2\omega_2|=|r_3\omega_3|$$

بنابراین، بین نسبت شعاع دو دایره و سرعت زاویه‌ای آنها رابطه زیر برقرار است.

$$\large |\frac{\omega_2}{\omega_3}|=|\frac{r_3}{r_2}|$$

فرض کنید قرار است یک کاهنده‌ سرعت را طوری طراحی کنیم که سرعت ورودی $$1800\:rev/min$$ را به سرعت خروجی $$1200\:rev/min$$ تبدیل کند. در اینجا سرعت با نسبت $$3:2$$ کم شده است. در نتیجه اگر به عنوان مثال، شعاع دایره گام پینیون $$4$$ سانتیمتر باشد، شعاع دایره گام چرخ دنده باید $$6$$ سانتیمتر در نظر گرفته شود.

چرخ دنده‌های 2 و ۳ را در شکل زیر در نظر بگیرید. با داشتن سرعت چرخ دنده شماره ۲ و تعداد دندانه‌ یا قطر گام هر دو چرخ دنده، سرعت چرخ دنده شماره ۳ به صورت زیر قابل محاسبه است.

$$\large n_3=|\frac{N_2}{N_3}n_2|=|\frac{d_2}{d_3}n_2|$$

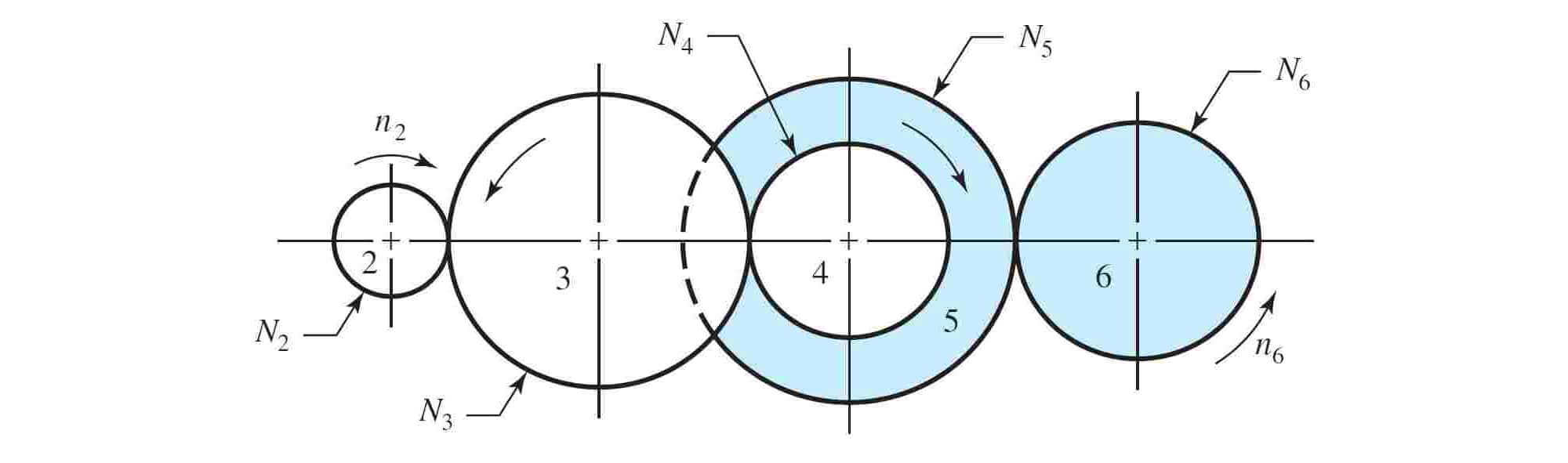
در رابطه بالا، $$n$$ سرعت برحسب دور در دقیقه، $$N$$ تعداد دندانه و $$d$$ هم قطر دایره گام را نشان می‌دهد. این رابطه، برای تمام انواع چرخ دنده (ساده، مارپیچ، مخروطی و حلزونی) قابل استفاده است. در طراحی‌ها پیشنهاد می‌شود نسبت تبدیل سرعت در دو چرخ دنده مجاور، از $$\large 10:1$$ بیشتر نشود. حال آنکه در شرایط عادی، از چرخ دنده ساده برای نسبت‌های سرعت‌ $$1:1$$ تا $$6:1$$ استفاده می‌شود. همین روش را می‌توان برای به دست آوردن سرعت چرخ دنده‌های بعدی نیز به کار برد. به عنوان مثال در شکل قبل، سرعت چرخ دنده شماره ۶ به صورت زیر به دست می‌آید.

$$\large n_6=|\frac{N_2}{N_3}\frac{N_3}{N_4}\frac{N_5}{N_6}n_2|$$

مثال ۱

سؤال: مجموعه دنده‌ای را در نظر بگیرید که از یک پینیون و یک چرخ دنده تشکیل شده است. پینیون، 16 دندانه و چرخ دنده ۴۰ دندانه دارد. گام قطری برابر ۲ است. ارتفاع سر دنده و پایه دنده، به ترتیب با $$\large \frac{1}{P}$$ و $$\large \frac{1.25}{P}$$ به دست می‌آید و زاویه فشار 20 درجه است. الف) گام، فاصله مرکز دو چرخ دنده و شعاع دایره‌های مبنا را محاسبه کنید. ب) هنگام سوار کردن این دو چرخ دنده روی محور، فاصله مرکز آنها به اشتباه، $$\large \frac{1}{4}\:in$$ بیشتر شده است. زاویه فشار و قطر دایره گام را در حالت جدید به دست آورید.

پاسخ: برای حل قسمت الف، ابتدا گام چرخ دنده را حساب می‌کنیم.

$$\large p=\frac{\pi}{P}=1.57 in$$

حال، قطر دایره گام را در پینیون و چرخ دنده به دست می‌آوریم.

$$\large d_P= \frac{N_P}{P}=\frac{16}{2}= 8\:in,~~~~~~ d_G= \frac{N_G}{P}=\frac{40}{2}= 20\:in$$

در نتیجه، فاصله بین مرکز دو چرخ دنده به صورت زیر است.

$$\large \frac{d_P+d_G}{2}=\frac{8+20}{2}= 14\:in$$

از آنجایی که زاویه فشار ۲۰ درجه است، شعاع دایره مبنا را از طریق رابطه زیر محاسبه می‌کنیم.

$$\large r_b=r\:\cos\phi\\~\\ \large \Rightarrow\begin{cases} r_{bP} =\frac{8}{2}\cos20^\circ = 3.76\:in \\ r_{bG} =\frac{20}{2}\cos20^\circ =9.40\:in \end{cases}$$

برای حل قسمت دوم سؤال، قطرهای جدید دایره گام را $$\large d_P^\prime$$ و $$\large d_G^\prime$$ می‌نامیم. در این حالت، فاصله مرکز دو چرخ دنده به صورت زیر به دست می‌آید.

$$\large \frac{d_P^\prime+d_G^\prime}{2} = 14.25\:in$$

از طرفی، می‌دانیم نسبت سرعت به شکل رابطه زیر است و تغییر نمی‌کند.

$$\large \frac{d_P^\prime}{d_G^\prime} = \frac{16}{40}$$

با ادغام دو رابطه اخیر، قطر جدید گام به دست می‌آید.

$$\large d_P^\prime =8.14\:in~~~~~ d_G^\prime =20.36\:in$$

با قرار دادن مقادیر مربوط به هریک از دو چرخ دنده، زاویه جدید فشار به صورت زیر قابل محاسبه است.

$$\large r_b=r\:\cos\phi\\~\\ \large \Rightarrow \phi^\prime =\cos^{-1}\frac{r_{bP}}{d_P^\prime/2}=\cos^{-1}\frac{3.76}{8.14/2}=22.59^\circ$$

محاسبه نیروها در چرخ دنده ساده

شکل زیر را در نظر بگیرید. دو چرخ دنده ساده باهم درگیر شده‌اند. پینیون با سرعت $$\large n_2$$ دور در دقیقه در جهت عقربه‌های ساعت در حال چرخش است. با حرکت پینیون، چرخ دنده نیز با سرعت $$\large n_3$$ دور در دقیقه می‌چرخد. نیروهای عکس‌العمل بین دندانه‌های این دو چرخ‌دنده ساده، در راستای خط فشار است.

نیرو و گشتاوری که از طرف محور $$\large a$$ به پینیون وارد می‌شود را به ترتیب با $$F_{a2}$$ و $$T_{a2}$$ نشان داده‌ایم. $$F_{32}$$ هم نیرویی است که چرخ دنده به پینیون وارد می‌کند. به طریقی مشابه، نیروها و گشتاور وارد به چرخ دنده نیز در جهت عکس است. مولفه $$t$$ نشان دهنده نیرو در جهت مماسی و مولفه $$r$$ نشان دهنده نیرو در جهت شعاعی است. نیروی انتقالی برابر با مولفه مماسی نیروی $$F_{32}$$ است و به صورت زیر تعریف می‌شود.

$$\large W_t=F_{32}^t=\frac{2T_{a2}}{d_2}$$

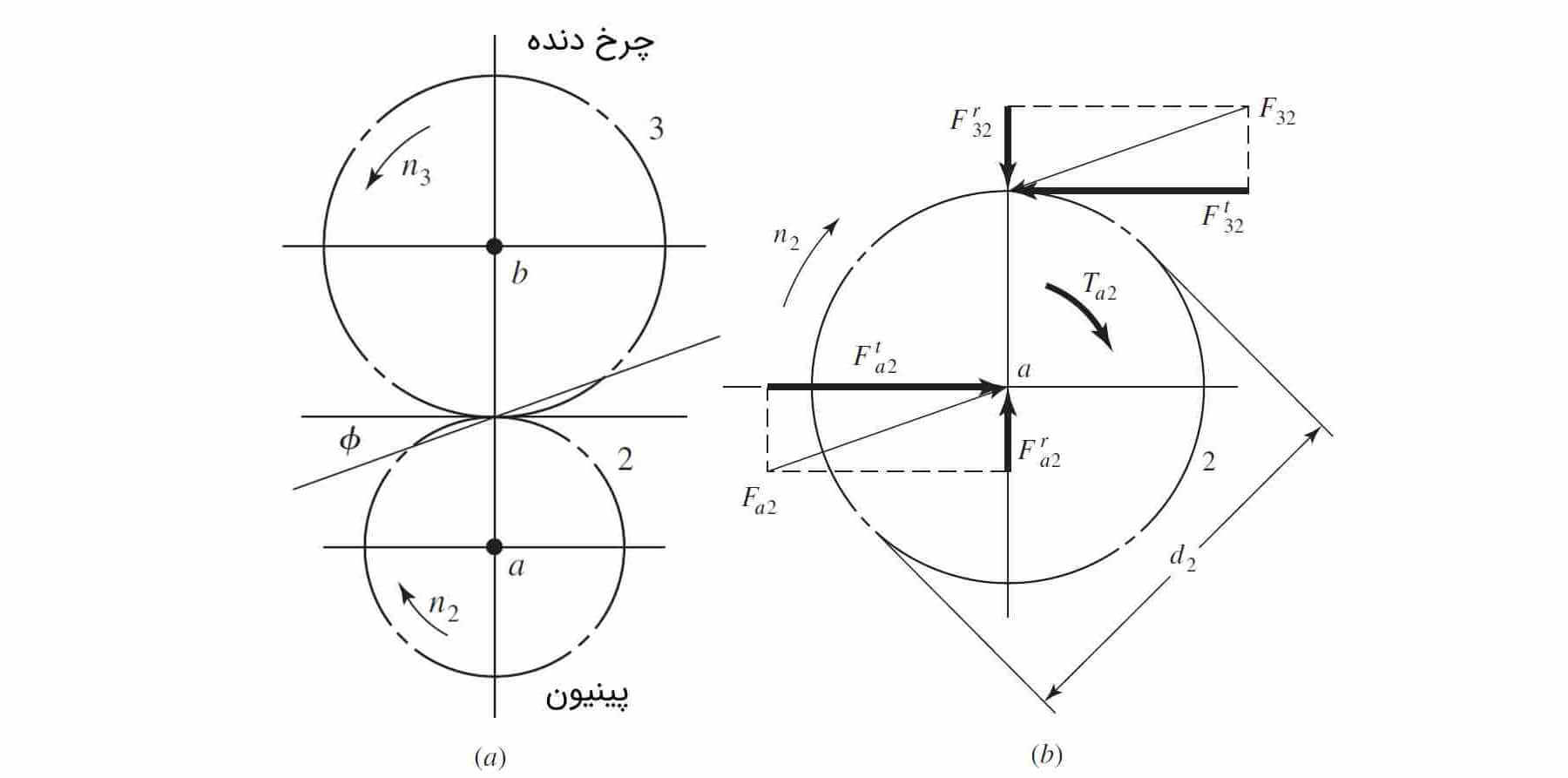
توجه کنید که مولفه شعاعی نیروی $$F_{32}$$، هیچ کمکی به انتقال نیرو نمی‌کند. همچنین توان انتقالی را نیز می‌توان با استفاده از رابطه زیر به دست آورد. توان انتقالی را با $$H$$ نشان می‌دهیم.

$$\large H=T\omega=(W_td/2)\omega$$

از آنجایی که راندمان چرخ دنده‌ها بالا و اصطکاک بین آنها ناچیز است، رابطه بالا را می‌توان با قرار دادن از $$d$$ و $$\omega$$ هر کدام از چرخ دنده‌ها محاسبه کرد. سرعت چرخ دنده را به صورت زیر هم می‌توان بیان کرد. رابطه زیر، سرعت خطی ذره‌ای را نشان می‌دهد که روی محیط دایره گام چرخ دنده قرار دارد.

$$\large V=(d/2)\omega~~\rightarrow~~V=\frac{\pi dn}{12}$$

در رابطه بالا، $$n$$ سرعت دوران چرخ دنده را به صورت دور در دقیقه نشان می‌دهد. نیروی انتقالی را می‌توان برحسب سرعت خطی چرخ‌دنده و در سیستم انگلیسی به صورت زیر بازنویسی کرد.

$$\large W_t=33,000 \:\frac{H}{V}$$

در این رابطه، $$W_t$$ نیروی انتقالی را با واحد $$lbf$$ نشان می‌دهد. توان انتقالی $$H$$ برحسب اسب بخار است و سرعت خطی به صورت فوت در دقیقه اندازه‌گیری می‌شود. سیستم $$SI$$، رابطه بالا را به شکل زیر تبدیل می‌کند. در این رابطه، توان به صورت کیلووات و نیروی انتقالی با واحد کیلو نیوتن محاسبه می‌شوند.

$$\large W_t=60,000 \:\frac{H}{\pi dn}$$

مثال ۲

سؤال: به شکل زیر توجه کنید. پینیون شماره ۲ با سرعت $$\large 1750\:rev/min$$ می‌چرخد و توانی برابر با $$\large 2.5\:kW$$ به چرخ دنده شماره ۳ منتقل می‌کند. زاویه فشار ۲۰ درجه و مدول چرخ دنده برابر با $$\large m=2.5\:mm$$ است. نیروهای وارد به چرخ دنده شماره ۳ را محاسبه کنید.

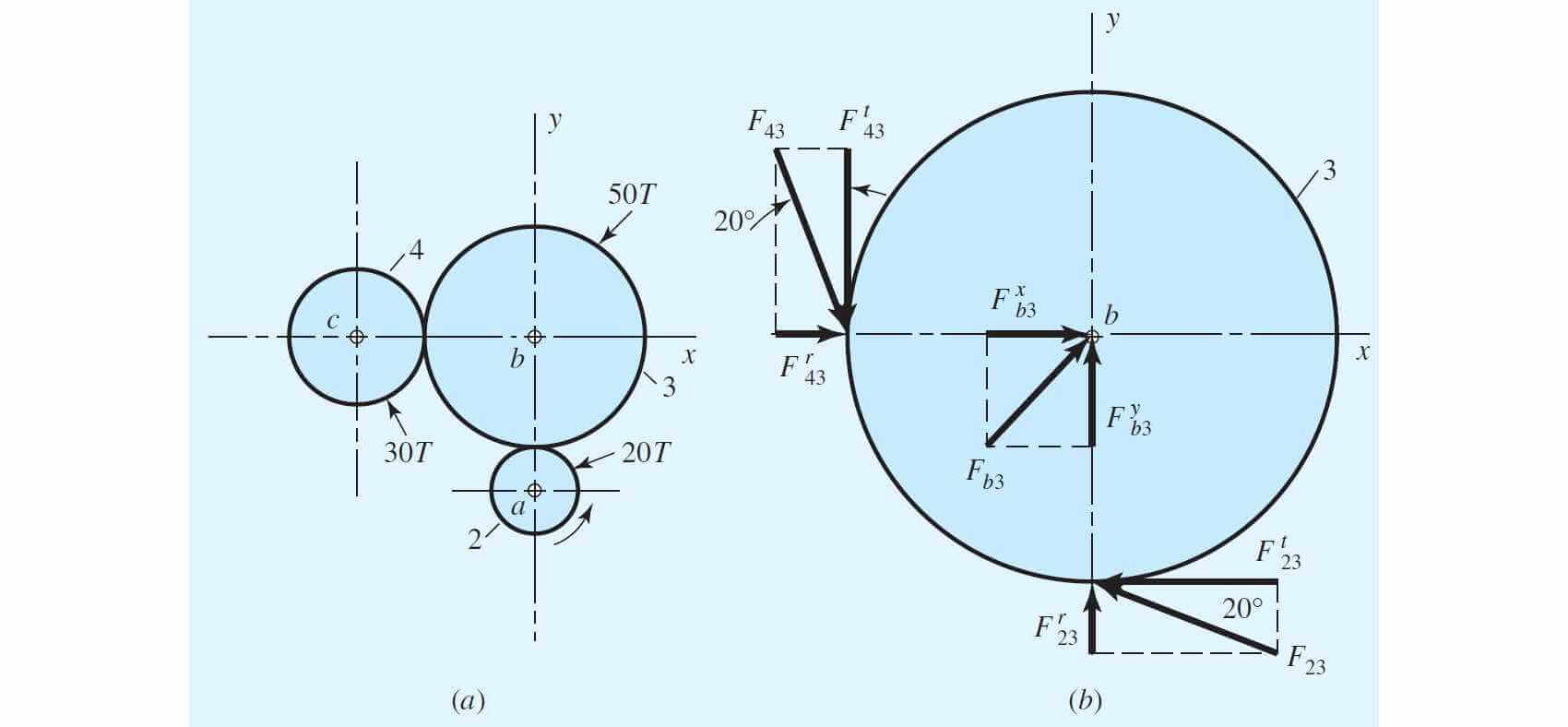
پاسخ: ابتدا قطر گام را در چرخ دنده‌های ۲ و ۳ محاسبه می‌کنیم.

$$\large d_2=N_2m=20\times2.5=50\:mm\\~\\ \large d_3=N_3m=50\times2.5=125\:mm$$

حال، نیروی انتقالی را با کمک رابطه زیر به دست می‌آوریم. در این رابطه، به جای سرعت $$\omega$$ از سرعت $$n$$ استفاده شده است که برحسب دور در دقیقه محاسبه می‌شود.

$$\large W_t=\frac{60,000H}{\pi dn}=\frac{60,000\times2.5}{\pi \times50\times1750}=0.546\:kN=F_{23}^t$$

اکنون با استفاده از زاویه فشار، به راحتی نیروی شعاعی و برآیند نیرویی که چرخ دنده ۲ به ۳ وارد می‌کند، به دست می‌آید.

$$\large F_{23}^r=F_{23}^t\times\tan 20^\circ = 0.546\times\tan 20^\circ = 0.199\:kN\\~\\ \large F_{23}=\frac{F_{23}^t}{\cos20^\circ}=0.581\:kN$$

چرخ دنده شماره ۳، هرزگرد است و توانی را به محور خود انتقال نمی‌دهد. بنابراین، نیروی مماسی چرخ دنده شماره ۴ به ۳ هم برابر $$\large W_t$$ است.

$$\large F_{43}^T =0.546\:kN,~~~~~F_{43}^r =0.199\:kN,~~~~~F_{43} =0.581\:kN$$

در نهایت، نیروی عکس‌العمل محوری را به صورت زیر به دست می‌آوریم.

$$\large F_{b3}^x =-(F_{23}^t +F_{43}^r ) =-(-0.546+0.199) =0.347kN\\~\\ \large F_{b3}^y =-(F_{23}^r +F_{43}^t ) =-(0.199-0.546) =0.347kN\\~\\ \large F_{b3}=\sqrt{(0.347)^2+(0.347)^2}=0.491\:kN$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• چرخ دنده – به زبان ساده
• نسبت چرخ دنده — به زبان ساده
• حرکت دایره ای – به زبان ساده