نرمال سازی با تبدیل باکس کاکس (Box–Cox) – به زبان ساده
بسیاری از تحلیلهای آمار کلاسیک، براساس توزیع نرمال صورت میگیرند. چنین تحلیلهایی معمولا به نام روشهای پارامتری شهرت دارند. در مقابل ممکن است حجم دادهها کم بوده یا میزان چولگی زیاد باشد و نتوان با استفاده از قضیه حد مرکزی CLT برای نرمال فرض کردن دادهها کمک گرفت. بنابراین گاهی به کمک بعضی از تبدیلات میتوان دادهها را با توزیع نرمال یکسو کرد. در این نوشتار به روش نرمال سازی با تبدیل باکس کاکس (Box-Cox) میپردازیم که از گروه تبدیلات توانی (نمایی) یا Power Transform است.
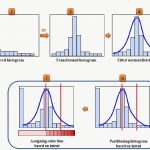
به منظور آشنایی بیشتر با شیوه تشخیص دادههای نرمال به مطلب نمودار چندک چندک (Q-Q plot) — به زبان ساده و آزمون نرمال بودن داده (Normality Test) --- پیاده سازی در پایتون مراجعه فرمایید. مطالعه توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها و قضیه حد مرکزی و تعمیم آن — به زبان ساده نیز خالی از لطف نیست.
نرمال سازی با تبدیل باکس کاکس (Box-Cox)
روش نرمال سازی با تبدیل باکس کاکس (Box-Cox) شیوهای برای تبدیل متغیرهای وابسته غیرنرمال به دادههایی با توزیع نرمال است. نرمال بودن چنین دادههایی فرض مهمی برای بسیاری از تکنیکهای آماری است. اگر دادههای شما دارای توزیع نرمال نباشند، با استفاده از نرمال سازی با تبدیل باکس کاکس (Box-Cox) میتوانید توزیع احتمالی آنها را تقریبا به توزیع نرمال نزدیک کنید تا بتوانید از مزایای روشهای پارامتری و آزمونهای پرتوان آن برای انجام تحلیلهای آماری کمک بگیرید.
تبدیل باکس کاکس، نوع خاصی از تبدیلهای توانی (Power Transformation) است. بنابراین بهتر است ابتدا با این نوع تبدیلها بیشتر آشنا شده، سپس به بررسی نرمال سازی با تبدیل باکس کاکس (Box-Cox) بپردازیم. این شیوه تبدیل توسط دو دانشمند انگلیسی آمار به نامهای «جورج باکس» (George Edward Pelham Box) و «دیوید کاکس» (Sir David Roxbee Cox) ابداع و مورد بررسی قرار گرفت. آنها نشان دادند که با استفاده از این تبدیل، توزیع دادههای غیر نرمال به توزیع نرمال نزدیک میشود.


تبدیل توانی (Power Transformation)
در آمار، تبدیل توانی (Power Transformation)، به خانوادهای از توابع گفته میشود که برای ایجاد یکنواختی روی دادهها با استفاده از توابع توانی (Power Functions) به کار میروند. این روشهای تبدیل در تحلیلهایی که احتیاج به تثبیت واریانس دارند یا ایجاد دادهها با توزیع نرمال هدف است و همچنین بهبود سنجش ارتباط بین متغیرها بخصوص توسط ضریب همبستگی پیرسون و ... مورد استفاده هستند.
فرض کنید مشاهدات یا دادهها به صورت یک بردار () با توجه به نوشته شده باشند در این حالت فرم کلی برای چنین تبدیلهایی به صورت زیر نوشته میشود.
رابطه ۱
در رابطه بالا، همان میانگین هندسی (Geometric Mean) مشاهدات است که به صورت زیر محاسبه میشود.
مشخص است که رابطه ۱، یک تابع دو ضابطهای است و براساس میانگین هندسی از مشاهدات ساخته شده است.
نکته: مثبت بودن دادهها در اینجا یک شرط محسوب میشود. ولی اگر دادهها چنین وضعیتی نداشته باشند، کافی است که هم مقادیر را با قدر مطلق کوچکتر مقدار جمع کنیم، به این ترتیب یک انتقال به سوی مقادیر نامنفی خواهیم داشت.
کاری که باکس و کاکس انجام دادند، استفاده از تابع درستنمایی توزیع نرمال و استفاده از ژاکوبین (Jacobian) تبدیل ذکر شده بود. در نظر بگیرید که تبدیلی به فرم زیر داشته باشید. قرار است که اعمال این تبدیل، یا شکلی از این تبدیل، روی مقادیر ها باعث بوجود آمدن دادههایی با توزیع نرمال شود.
ژاکوبین این تبدیل به صورت زیر نوشته میشود.
به این ترتیب میانگین هندسی در این تبدیل ظاهر میشود. به همین ترتیب تابع درستنمایی (Likelihood Function) حداکثر مقدار خود را به صورت زیر خواهد داشت.
از آنجایی که تمایل داریم توزیع به صورت نرمال درآید، تابع درستنمایی را برحسب توزیع نرمال نوشتهایم. در نتیجه با تکنیک مجموع مربعات روی حداقل و در نتیجه تابع لگاریتم تابع درستنمایی حداکثر خواهد شد. این گزاره یکی از خصوصیات توزیع نرمال است.
تبدیل باکس کاکس (Box-Cox)
براساس رابطه ۱، تبدیل باکس کاکس (Box-Cox) تعریف میشود. در حالت تک پارامتری، این تبدیل به صورت زیر نوشته میشود.
رابطه ۲
به این ترتیب مقادیر تبدیل شده و به صورت در میآیند. البته در این حالت باید شرط وجود داشته باشد در غیراینصورت ضابطه دوم مربوط به رابطه ۲ در حالتی که قابل محاسبه نیست.
فرم دیگری نیز از تبدیل باکس کاکس وجود دارد که به صورت دو پارامتری است. این تبدیل در رابطه ۳ دیده میشود.
رابطه ۳
که در آن باید باشد.
در جدول زیر بعضی از این تبدیلات به ازاء مقدارهای مختلف دیده میشود.
| Common Box-Cox Transformations
تبدیل باکس کاکس تک پارامتری برحسب مقدارهای مختلف | |
| Lambda value () | Transformed data () |
|
| |
|
| |
برای تعیین مقدار مناسب در تبدیل باکس کاکس، معمولا روشهای تبدیل را با پارامترهای مختلف روی دادهها به کار برده و با استفاده مقدار حداکثر تابع درستنمایی، بهترین مقدار پارامتر را انتخاب میکنند. البته این امر را با تکنیکهای سنجش نرمال بودن دادهها نظیر Q-Q plot و یا آزمونهای نرمال بودن نیز میتوان مشخص کرد که کدام مقدار بهترین تبدیل برای ایجاد دادههای نرمال برای نمونه اصلی است.
نرمال سازی با تبدیل باکس کاکس (Box-Cox) در نرمافزارهای محاسبات آماری
در اغلب نرمافزارهای محاسبات آماری گزینهای برای استفاده از این تبدیل وجود دارد. برای مثال اگر بخواهیم در زبان برنامهنویسی محاسبات آماری R از تبدیل باکس کاکس استفاده کنیم، کافی است تابع boxcox را به کار بریم. همچنین در پایتون نیز تابعی در کتابخانه SCiPy وجود دارد که وظیفه انجام محاسبات مربوط به تبدیل باکس کاکس را انجام میدهد.
در ادامه به بررسی دو مثال میپردازیم که در اولی به کمک R و تابع boxcox و در دومی به زبان پایتون (Python) و با تابع stats.boxcox عمل تبدیل صورت گرفته است. در انتها نیز به کمک نمودار Q-Q plot صحت نرمال بودن دادههای تبدیل یافته را مورد بررسی قرار میدهیم.
مثال ۱
در این جا به کمک یک نمونه صدتایی از توزیع یکنواخت در بازه ۱ تا ۵ دادههایی تولید میکنیم که در مدل به عنوان متغیر مستقل ثبت شده است. از طرفی به کمک این دادهها، یک رابطه خطی به صورت مکعب ایجاد میکنیم. البته برای اینکه مدل تصادفی شود، به هر یک از مقادیر مکعب شده، میزان خطای یا نوفه سفید (White Noise) از توزیع نرمال استاندارد نیز اضافه میکنیم. بنابراین خواهیم داشت:
کدهایی که در ادامه مشاهده میکنید به این منظور تهیه شدهاند.
حال قرار است پارامترهای این مدل خطی (رابطه بین و ) را بدست آوریم.
ابتدا یک مدل خطی ساده ایجاد کرده و سپس به کمک تبدیل باکس کاکس، مدل جدیدی را برازش میکنیم. نتایج مربوط به مدل خطی ساده در متغیر m و نتایج مربوط به تبدیل باکس کاکس در متغیر bc ذخیره شدهاند.
همانطور که در کد دیده میشود، به کمک تابع boxcox بهترین مقدار پارامتر تبدیل نیز حاصل شده است. همچنین نموداری که براساس آن مقدار تابع درستنمایی حداکثر شده نیز مشخص شده است. مشخص است که مقدار پارامتر است.
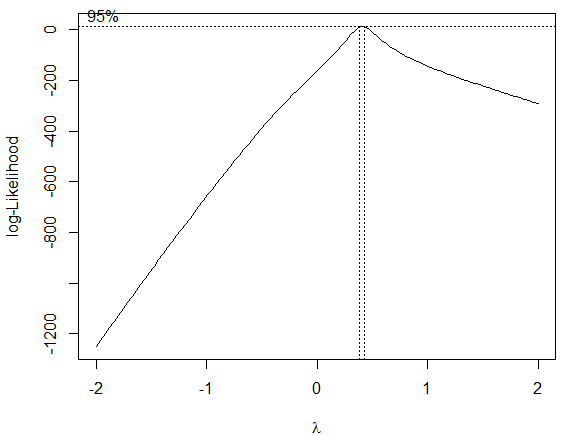
حال تبدیل را به کمک تابعی که در کد زیر با نام poweTransform نوشتهایم انجام میدهیم.
در انتها نیز مدل را به کمک دادههای تبدیل یافته و پارامتر برازش میدهیم.
در انتها نیز مقایسهای بین مدل برازش حاصل از رگرسیون خطی ساده و همچنین مدل رگرسیونی با تبدیل باکس کاکس ارائه شده است. در انتها نمودارهای چندک- چندک Q-Q plot، نمایشگر نزدیکی باقیمانده مدل رگرسیونی به توزیع نرمال در دادههای تبدیل شده است.
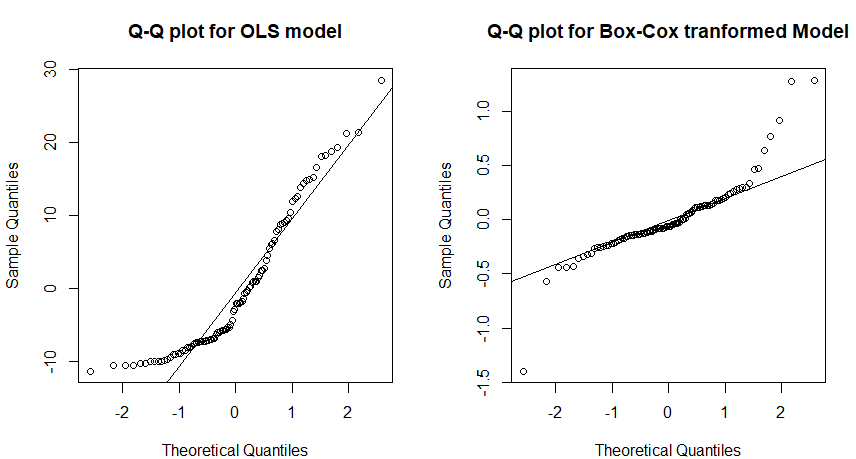
همانطور که دیده میشود، نمودار سمت راست، به جز در چند مورد خاص، برازش بهتری را برای دادهها با توزیع نرمال نشان میدهد، در حالیکه در نمودار سمت چپ، بسیاری از مقدارها (باقیماندههای حاصل از مدل رگرسیونی) از توزیع نرمال پیروی نمیکنند.
مثال ۲
در این مثال به کمک یک مجموعه داده واقعی که مربوط به پروازهای یک فرودگاه است، عمل تبدیل را انجام میدهیم. این مجموعه داده را میتوانید از (+) دریافت کنید. این فایل به قالب فشرده است ولی اگر آن را از حالت فشرده خارج کنید متوجه میشوید که در آن فایلی به نام sample_data.csv وجود دارد که توسط اکسل قابل نمایش است.
کدها زیر به منظور فراخوانی و به کارگیری این فایل نوشته شده است. در این قطعه کد از کتابخانههای Pandas و mathlibplot استفاده شده است.
همانطور که مشاهده میکنید، نمودار فراوانی این دادهها به نظر چوله میرسد بنابراین به کمک تبدیل باکس کاکس میتوان آن را به نرمال تبدیل کرد.
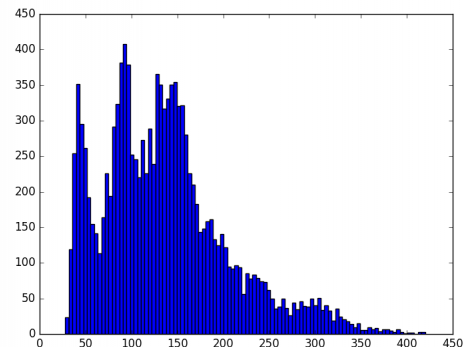
در تصویر بالا، چولگی به سمت راست در نمودار فراوانی یا هیستوگرام (Histogram) به خوبی دیده میشود.
حال برنامه زیر که به منظور نرمال سازی با تبدیل باکس کاکس (Box-Cox) نوشته شده است را اجرا میکنیم. در این بین برای نرمال سازی با تبدیل باکس کاکس (Box-Cox) از کتابخانه Scipy کمک گرفتهایم. تابع stats.boxcox در این کتابخانه به این امر اختصاص داده شده است.
پس از اجرای این کار، نمودار فراوانی نشان از نرمال بودن دادههای تبدیل یافته میدهد. مقدار پارامتر این تبدیل در متغیر lam ذخیره شده است. پس از اجرا، مقدار برآورد برای پارامتر برابر با 8.4721 خواهد بود.
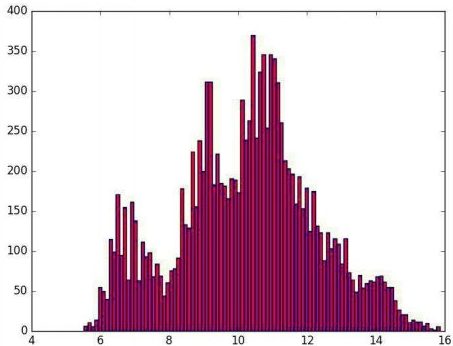
این نمودار نیز نشان میدهد که چقدر دادهها به توزیع نرمال نزدیک شدهاند. در تصویر زیر مقایسهای بین حالت اولیه دادهها و تبدیل یافته آنها توسط روش باکس کاکس مشاهده میشود. مشخص است که چولگی تا حد زیادی از بین رفته است.
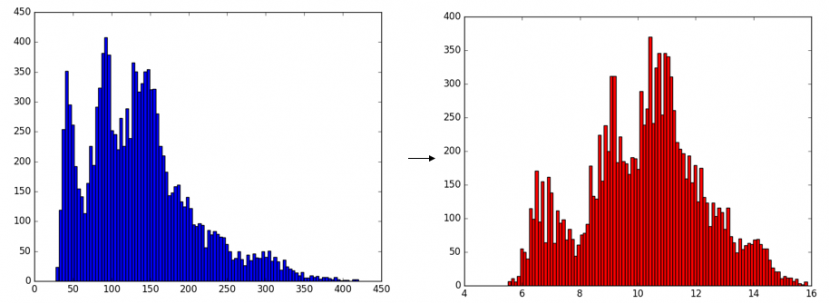
توجه داشته باشید که نرمال سازی با تبدیل باکس کاکس (Box-Cox) میتواند روی دادهها به کار رود و امکان پیشبینی توسط مدل بهبود مییابد ولی مواردی نیز وجود دارد که این تبدیل باعث انحراف و عدم بهبود مدل میشود. برای مثال در دادههای دم-سنگین (Heavy tail) استفاده از تبدیل باکس کاکس باعث میشود که مدلهای رگرسیونی ایجاد شده توسط تکنیک رگرسیون OLS مناسب تشخیص داده نشوند. در این موارد بهتر است تکینکهای دیگر رگرسیون مانند رگرسیون ستیغی (Ridge Regression)، رگرسیون لار (LAR Regression) یا لاسو (Lasso Regression) مورد استفاده قرار گیرند.
خلاصه و جمعبندی
در این نوشتار با مفاهیم اولیه و شیوه اجرای نرمال سازی با تبدیل باکس کاکس (Box-Cox) آشنا شدیم و نحوه محاسبه آن را براساس پارامترهای مختلف، فرا گرفتیم. همچنین با استفاده از دو مثال در محیط برنامه نویسی R و پایتون، شیوه اجرای این تبدیلات مشاهده کرده و نحوه اجرای دستورات مرور شد.
البته باید به این نکته نیز توجه داشت که همیشه نمیتوان با استفاده از این تبدیلات، دادهها را به شکلی درآورد که توزیع دادههای جدید، نرمال باشد. این امر بخصوص در مورد دادههای دم سنگین خطرناک است و باعث میشود که نتایج حاصل معتبر نباشند. یکی از دلایل مهم در این زمینه ناموجود بودن واریانس برای چنین توزیعهایی است در حالیکه در نرمال سازی با تبدیل باکس کاکس (Box-Cox) فرض وجود واریانس از شرطهای اصلی محسوب میشود.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار و احتمالات
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای برنامه نویسی R و نرم افزار RStudio
- توزیعهای آماری — مجموعه مقالات جامع وبلاگ فرادرس
- نمودار چندک چندک (Q-Q plot) — به زبان ساده
- توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
^^












