تقریب عدد پی با روش سوزن بوفون – پیاده‌سازی در متلب و پایتون

عدد پی که با نماد $$\pi$$ نشان داده می‌شود، یک عدد حقیقی و گنگ است که در ریاضیات، فیزیک و مهندسی کاربرد فراوانی دارد. این عدد اغلب به عنوان نسبت محیط دایره به قطر آن تعریف می‌شود. اگر تاریخچه عدد پی را مطالعه کنید، خواهید دید که دانشمندان زیادی تلاش کرده‌اند مقدار این عدد را با دقتی بیش از آنچه که وجود داشته است، تقریب بزنند و از این رو، روش‌های مختلفی را برای این منظور به کار برده‌اند. در این آموزش، یکی از این روش‌ها را برای تقریب عدد پی معرفی می‌کنیم. مسئله سوزن بوفون یا قضیه سوزن بوفون، عنوان روشی است که با آن آشنا می‌شویم.

مسئله سوزن بوفون (Buffon's Needle Problem) به پرسشی بر می‌گردد که «ژرژ-لوئی لکرک کنت دو بوفون» (Georges-Louis Leclerc, Comte de Buffon)، ریاضی‌دان، زیست‌شناس و ستاره‌شناس فرانسوی، در قرن هجدهم آن را مطرح کرد:

فرض کنید سطحی داریم که از نوارهای چوبی موازی با عرض یکسان ساخته شده است. سوزنی را روی این سطح می‌اندازیم. احتمال اینکه سوزن خط بین دو نوار را قطع کند (با آن متقاطع باشد) چقدر است؟

در ادامه، نسخه ساده و عمومی از مسئله سوزن بوفون برای تقریب عدد پی را شرح خواهیم داد. همچنین، برای کسانی که به برنامه‌نویسی علاقه‌مندند، کدهای متلب و پایتون تقریب عدد پی با استفاده از روش بوفون ارائه شده است.

نسخه ساده تقریب عدد پی با روش سوزن بوفون

فرض کنید مجموعه‌ای از نوارهای چوبی در کنار یکدیگر به طور موازی قرار گرفته‌اند که عرض هرکدام از آن‌ها برابر با یک واحد است.

سوزنی به طول یک واحد را روی این سطح چوبی می‌‌اندازیم.

نمودار یک سوزن بعد از قرار گرفتن روی سطح، مطابق شکل زیر است. از آنجایی که سوزن کاملاً تصادفی روی سطح انداخته می‌شود، موقعیت آن را می‌توان با دو متغیر مستقل بیان کرد. متغیر اول $$d$$ است که فاصله نقطه میانی سوزن از نزدیک‌ترین لبه نوار چوبی را نشان می‌دهد. متغیر دوم نیز $$\theta$$ است که معرف زوایه سوزن نسبت به خطوط موازی است.

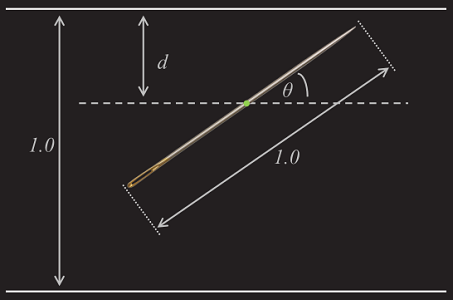
در نمودار شکل بالا سوزن خط لبه نوار را قطع نکرده است. اما چه زمانی سوزن خط را قطع می‌کند؟ با توجه به نمودار بالا، سوزن زمانی خط لبه نوار چوبی را قطع می‌کند که اندازه $$d$$ کوچک‌تر یا مساوی $$\frac {1 }{2} \sin \theta$$ باشد. این گفته را به صورت بصری بررسی می‌کنیم.

اندازه زاویه $$\theta$$ بین 0 و $$\pi$$ است (طبق خاصیت تقارن، اگر زاویه بیش از این مقدار باشد، گویی که سوزن مشابهی در جهت معکوس قرار گرفته است). همچنین، طبق آنچه که گفتیم، اندازه $$d$$ می‌تواند بین 0 و $$\frac { 1 } { 2 }$$ باشد (نقطه میانی سوزن هیچگاه نمی‌تواند فاصله‌ای بیش از $$\frac {1}{2}$$ از هریک از لبه‌ها داشته باشد).

هر ترکیبی (با احتمال برابر) از $$\theta$$ و $$d$$ را می‌توان با نقطه‌ای روی نمودار زیر نشان داد. با اعمال شرط $$d \le 1/2 \sin \theta$$ برای تقاطع سوزن و خط، ناحیه مشخص شده شکل زیر را خواهیم داشت. بنابراین، احتمال اینکه سوزن خط را قطع کند، برابر با نسبت ناحیه مشخص (آبی) به کل مساحت مستطیل است.

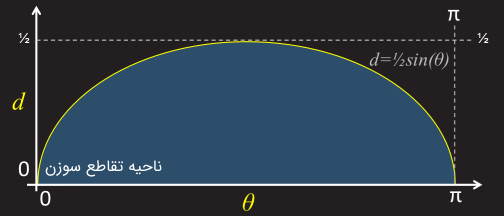
مساحت کل فضای جواب برابر با $$\frac{1}{2}\pi$$ است. مساحت ناحیه آبی نیز برابر با انتگرال معین عبارت $$\frac{1}{2} \sin \theta$$ از ۰ تا $$\pi$$ است.

$$\large A = \int _ 0 ^ \pi { \frac { 1 } { 2 } } \sin \theta d \theta$$

$$\large A = \left [ - \frac{ 1 } { 2 } \cos \theta \right ] _ 0 ^ \pi = \left [ \frac { 1 } { 2 } \right ] - \left [ - \frac { 1 } { 2 } \right ] = 1$$

احتمال اینکه سوزن از یک لبه عبور کند و با آن متقاطع باشد، برابر با نسبت مساحت زیر منحنی بر مساحت کل مستطیل است:

$$\large Pr = \frac { 1 } { \pi / 2 } = \frac { 2 } { \pi }$$

این بدین معنی است که اگر آزمایش انداختن سوزن را بارها و بارها تکرار کرده و تعداد دفعاتی که سوزن خطوط موازی را قطع می‌کند، ثبت کنیم، می‌توانیم تقریبی از عدد $$\pi$$ را به دست آوریم. به عبارت دیگر، اگر تعداد دفعات انداختن سوزن را در دو ضرب کرده و آن را بر تعداد دفعاتی که سوزن با خط تقاطع داشته، تقسیم کنیم، تقریب عدد $$\pi$$ به دست می‌آید.

برای مثال، اگر سوزنی را ۱۰۰ بار بیندازیم و ۶۴ بار از آن خط را قطع کند، تقریب عدد $$\pi$$ برابر با $$\frac {2 \times 100} { 64}$$ خواهد بود که تقریباً برابر با ۳٫۱۲۵ است. بدیهی است که برای گرفتن نتایج دقیق‌تر، باید تعداد دفعات آزمایش را افزایش دهیم.

نسخه عمومی تقریب عدد پی با روش سوزن بوفون

آنچه در بخش قبل شرح دادیم، حالت ساده‌ای بود که یک سوزن با طولی برابر با فاصله خطوط، روی سطح انداخته می‌شد.

فیلم آموزش کتابخانه NumPy برای محاسبات علمی در پایتون (رایگان) در فرادرس

کلیک کنید

حال مسئله را با نگاهی کلی‌تر بررسی می‌کنیم.

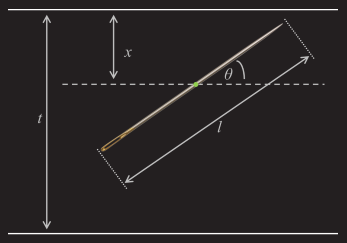
فرض کنید سوزنی به طول $$l$$ داریم و فاصله بین خطوط موازی برابر با $$t$$ است. در این صورت باید دو حالت را بررسی کنیم:

• در حالت اول، سوزن کوتاه است ($$l \le t$$). برای یک سوزن کوتاه، بسته به زاویه‌ای که روی سطح قرار می‌گیرد، ممکن است خطی را قطع کند.
• در حالت دوم، اگر سوزن بلند باشد ($$l > t$$)، علاوه بر اینکه می‌تواند بین خطوط قرار بگیرد یا یکی از آن‌ها را قطع کند، حداقل زاویه‌ای برای آن وجود دارد که به ازای مقادیر بزرگ‌تر از این زاویه، سوزن حداقل یکی از خطوط را قطع خواهد کرد.

حالت اول (سوزن کوتاه)، مشابه مورد ساده‌ای است که در بخش قبل آن را بررسی کردیم. احتمال برابر با نسبت ناحیه تقاطع سوزن و خط به کل فضای جواب است. اکنون کل فضای جواب (مخرج)، بزرگ‌تر است ($$t \pi$$) و اندازه ناحیه نیز برابر با $$\frac { l } { 2 } \sin \theta$$ خواهد بود. برای هر زاویه ممکن قرارگیری سوزن کوتاه روی سطح، احتمال برابر است با:

$$\large \operatorname {Pr} = \frac { \int _ { 0 } ^ { 2 \pi } \frac { l } { 2 } | \sin \theta | d \theta } { \pi t } = \frac { 4 \int _ { 0 } ^ { \pi / 2 } \frac { l } { 2 } | \sin \theta | d \theta } { \pi t }$$

که حاصل آن به صورت زیر است:

$$\large \operatorname {Pr} =\frac { 2 l } { \pi t }$$

اگر $$\frac {l}{t} = 1$$ را در رابطه اخیر قرار دهیم، می‌بینیم که نتیجه، مشابه مورد ساده‌ای است که در بخش قبل بررسی کردیم.

اکنون، حالت دوم را در نظر می‌گیریم که مربوط به سوزن بلند است و بررسی آن از نظر هندسی اندکی پیچیده‌تر است. دلیل این پیچیدگی آن است که در زوایای خاصی، صرف‌نظر از موقعیت نقطه میانی، سوزن یکی از خطوط را قطع می‌کند. معادله زیر احتمال را براساس طول سوزن و عرض تخته‌ها بیان می‌کند:

$$\large \operatorname {Pr} = \frac { 2 } { \pi } \cos ^ { - 1 } \left ( \frac { t } { l } \right ) + \frac { 2 l } { \pi t } ( 1-\sqrt { 1 - \left ( \frac { t } { l } \right ) ^ { 2 } } )$$

برای ساده کردن معادله بالا، نسبت طول سوزن به عرض تخته‌ها را $$x$$ فرض می‌کنیم و در نتیجه، خواهیم داشت:

$$\large \begin {array} {c} { x = \frac { l } { t } \quad \operatorname {Pr} = \frac { 2 } { \pi } \left ( x - \sqrt { x ^ { 2 } - 1 } + \sec ^ { - 1 } x \right ) } \\ { \operatorname {Pr} = \left \{ \begin {array} {cc} { \frac { 2 x } { \pi } \quad x \leq 1 } \\ { \frac { 2 } { \pi } \left ( x - \sqrt { x ^ { 2 } - 1 } + \sec ^ { - 1 } x \right ) } \end {array} \right . } \end{array}$$

معادله بالا در شکل زیر رسم شده است که در آن، محور افقی مقدار $$x$$ و محور عمودی مقدار احتمال را نشان می‌دهد.

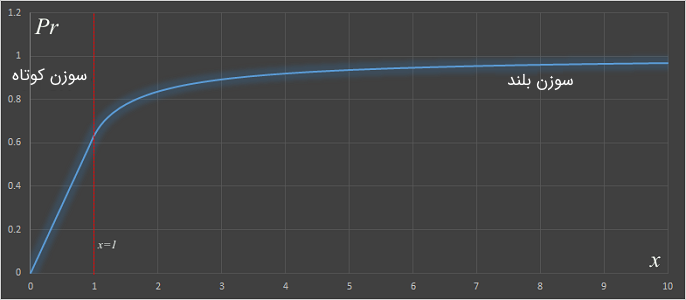
همان‌طور که نمودار بالا نشان می‌دهد، وقتی سوزن کوتاه باشد، احتمال خطی خواهد بود. همچنین، وقتی سوزن بلند باشد، با بزرگ‌تر شدن نسبت طول سوزن به عرض نوارها، احتمال به یک مقدار قطعی میل می‌کند.

جالب است بدانید که در سال ۱۹۰۱، ریاضی‌دان ایتالیایی، ماریو لازارینی (Mario Lazzarini)، آزمایش سوزن بوفون را انجام داد. او یک سوزن را ۳۴۰۸ بار انداخت و تقریب شناخته شده $$\frac {355}{113}$$ را تا شش رقم اعشار برای $$\pi$$ به دست آورد.

پیاده‌سازی تقریب عدد پی با روش بوفون در متلب

در این بخش،‌ طبق آنچه که درباره روش بوفون گفتیم، تقریب عدد پی را در متلب پیاده‌سازی می‌کنیم. این کار را به سادگی و طی مراحلی که در ادامه می‌آید، انجام می‌دهیم.

فیلم مجموعه آموزش متلب MATLAB – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

تعریف پارامترها

قبل از همه چیز، تعداد سوزن‌ها را تعیین (در اینجا ۱۰۰۰) و آن را به صورت زیر تعریف می‌کنیم:

1N = 1000;

طول هر سوزن را نیز ۰٫۲ در نظر می‌گیریم:

1L = 0.20;

می‌خواهیم نقاط ابتدای سوزن‌ها بین $$L$$ و $$1 - L$$ باشند، بنابراین، به بیرون از مربع واحد نمی‌رویم.

1xb = L + rand(1,N)*(1-2*L);
2yb = L + rand(1,N)*(1-2*L);
3angs = rand(1,N)*360;
4xe = xb + L*cosd(angs);
5ye = yb + L*sind(angs);

رسم سوزن‌ها

اکنون، پس از تعریف پارامترها و سوزن‌ها، برای درک بهتر، آن‌ها را رسم می‌کنیم. برنامه لازم برای رسم این خطوط به صورت زیر است:

1ax = axes;
2plot(ax,[xb;xe],[yb;ye])
3axis square

شکل زیر، از اجرای این برنامه به دست آمده است.

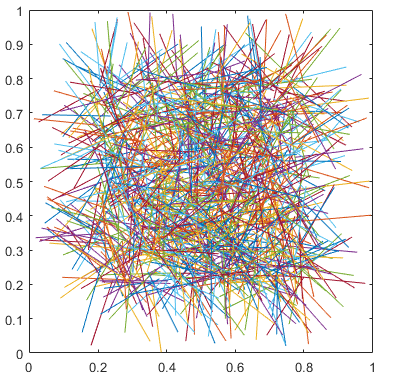
تعریف خطوط موازی

اکنون خطوط موازی را با دستور‌های زیر مشخص می‌کنیم که فاصله ‌آن‌ها از هم برابر با $$L$$ است:

1hold on
2glines = 0:L:1;
3for i = 1:length(glines)
4   xline(ax, glines(i));
5end

خطوط موازی در شکل زیر مشخص شده‌اند.

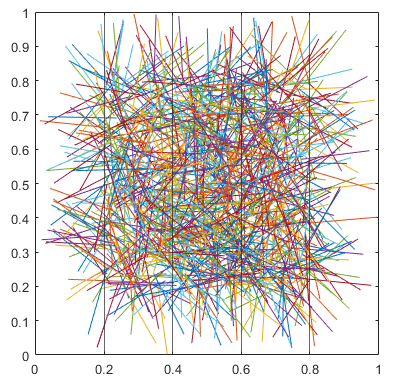
شمارش تعداد سوزن‌های متقاطع و تقریب پی

با اجرای دو دستور زیر، مقدار تقریبی $$pi$$ به دست می‌آید:

1n = sum(floor(xb/L) ~= floor(xe/L));
2piEstimate = 2 * N / n

در مورد خاص این مثال، نتیجه برابر است با:

piEstimate = 3.1153

رسم نمودار نهایی

با دستور زیر، شکل نهایی رسم خواهد شد که شامل سوزن‌ها، خطوط موازی و مقدار تقریبی به دست آمده عدد $$\pi$$ است.

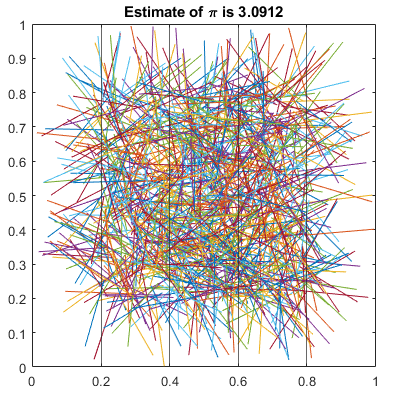
برنامه کامل متلب برای تقریب عدد پی با استفاده از روش بوفون به صورت زیر است:

1%% Estimating pi Using Buffon's Method
2% I recently attended the ICIAM meeting in Valencia, Spain which meant I
3% got to hang out with my pals Carlos Sanchis and
4% <https://www.mathworks.com/matlabcentral/profile/authors/1296922-lucas-garc%C3%ADa
5% Lucas Garcia> :-)!  Carlos showed me a problem he was working with
6% Professor Fernando Giménez from UPV regarding an app for estimating $\pi$
7% using <https://en.wikipedia.org/wiki/Buffon%27s_needle_problem Buffon's
8% method>. Here's the problem statement from Wikipedia:
9% 
10% _Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor._
11% _What is the probability that the needle will lie across a line between two strips?_
12%
13% Interesting that the original intention had nothing to do with computing
14% $\pi$ !  There's some fun, powerful, yet fairly easy code to demonstrate
15% the algorithm.
16%% Set Up Parameters
17% How many line segments?
18N = 1000;
19%%
20% Length of each line?
21L = 0.20;
22%%
23% We want the beginning points of the lines to lie between L and 1-L so we
24% don't go outside the unit square.
25xb = L + rand(1,N)*(1-2*L);
26yb = L + rand(1,N)*(1-2*L);
27angs = rand(1,N)*360;
28xe = xb + L*cosd(angs);
29ye = yb + L*sind(angs);
30%% Visualize the Lines
31ax = axes;
32plot(ax,[xb;xe],[yb;ye])
33axis square
34%% Show the Vertical Grid Lines Defined by L Spacing
35hold on
36glines = 0:L:1;
37for i = 1:length(glines)
38   xline(ax, glines(i));
39end
40%% Count the Segments Intersecting the Grid
41n = sum(floor(xb/L) ~= floor(xe/L));
42piEstimate = 2 * N / n
43%% Annotate Final Plot
44title("Estimate of \pi is " + piEstimate)
45%% What Happens as L and N change?
46% This could be a great exercise for the classroom - seeing how the
47% estimates depend on how many line segments and the spacing of the grid.
48% Not to mention running a bunch of times with different random numbers
49% each time.  What simple estimation problems do you like to use?  Let me
50% know <https://blogs.mathworks.com/loren/?p=3416#respond here>.
51
52%%
53% _Copyright 2019 The MathWorks, Inc._

پیاده‌سازی تقریب عدد پی در پایتون

برنامه پایتون تقریب عدد پی با استفاده از روش بوفون، به صورت زیر است:

1'''
2From Statistical Mechanics by Werner Krauth
3
4Buffon's Needle Experiment
5n = number of throws
6r = number of runs
7a = length of needle
8b = distance between cracks
9theta = angle needle makes to crack
10rcenter = center of needles on floor
110  < theta < pi/2
120 < xcenter < b/2
13
14nhits <===  number of hits of needle centered at x, with orientation theta
15nhits = 1 if x < a/2 and abs(theta) < arcos(x/(a/2))
16      = 0 otherwise
17'''
18
19import random
20import math
21
22def buffon(n,r,a,b):
23    data=[]
24    print 'Buffon Needle Experiment (Google it) ' 
25    print 'Runs       Number Hits  estimate of pi'
26    for jj in range(r):
27        nhits = 0
28        for ii in range(n):
29            xcent = random.uniform(0,b/2.0)
30            theta = random.uniform(0,math.pi/2)
31            xtip  = xcent - (a/2.0)*math.cos(theta)  #use of cosine not historically accurate
32            if xtip < 0 :
33                nhits += 1
34        #print str(jj)+'            '+str(nhits)+'               '+str((6.0/a*float(b))*nhits/n)
35        c = 2.0*a*n
36        d = b*nhits
37        print str(jj)+'            '+str(nhits)+'               '+str(c/d)
38        data.append([jj,nhits])
39    return data
40        
41
42r=5
43n=4000
44a = 2  #needle 2 inches
45b = 2  #cracks 2 inch spacing
46
47hits= buffon(n,r,a,b)

نتیجه حاصل از اجرای این برنامه به صورت زیر خواهد بود:

Buffon Needle Experiment (Google it)
Runs Number Hits estimate of pi
0 2557 3.12866640594
1 2535 3.15581854043
2 2564 3.12012480499
3 2550 3.13725490196
4 2595 3.08285163776

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های محاسبات عددی
• آموزش محاسبات عددی با MATLAB
• مجموعه آموزش‌های دروس ریاضیات
• آموزش ریاضی پایه دانشگاهی
• شبیه سازی مونت کارلو (Monte Carlo Simulation) – محاسبه انتگرال‌ به روش عددی
• روش نیوتن — به زبان ساده
• تقریب خطی — به زبان ساده

^^