تابع یک به یک و پوشا — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

پیش‌تر در بلاگ فرادرس مفاهیم تابع، ترکیب آن‌ها و دامنه و برد تابع شرح داده شدند. در این مطلب قصد داریم تا دو نوع پرکاربرد از توابع، تحت عنوان تابع «پوشا» (Surjective) و تابع «یک به یک» (Injective) را توضیح دهیم.

تعاریف

تابع، مفهومی است که می‌توان با استفاده از آن اعضای دو مجموعه هم‌چون مجموعه A را به اعضای مجموعه‌ی B نسبت داد.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

توجه داشته باشید که این نسبت دادن بایستی به شکلی خاص باشد تا بتوان ارتباط ایجاد شده را تابع نامید. از طرفی اگر هر عضو از مجموعه A تنها یک عضو را از مجموعه B انتخاب کند، تابع ایجاد شده از نوع یک به یک خواهد بود. در شکل زیر حالت‌های مختلف ارتباط بین اعضای دو مجموعه نشان داده شده است.

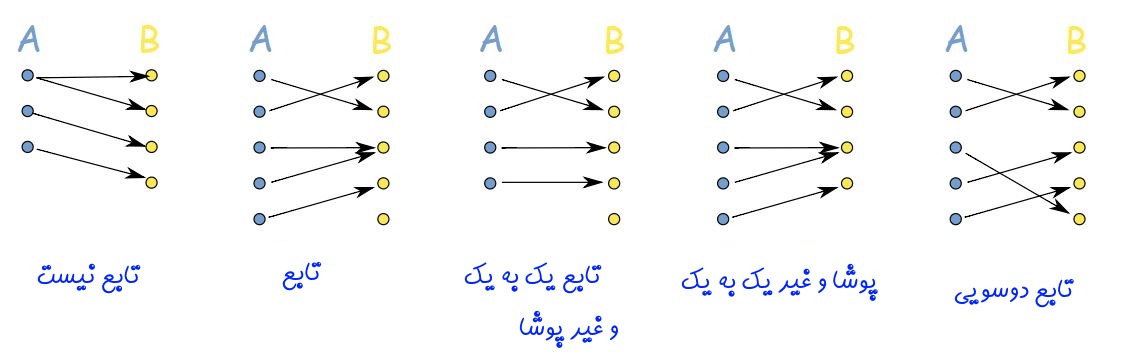
در ادامه هریک از مفاهیم فوق را به تفکیک توضیح خواهیم داد.

تابع

همان‌طور که در بالا نیز عنوان شد، تابع، مفهومی است که در آن هر عضو از یک مجموعه به عضوی متناظر در مجموعه‌ای دیگر مرتبط می‌شود. بنابراین مطابق با شکل زیر اگر یک عضو از مجموعه A، به دو عضو از مجموعه B اختصاص داده شود، ارتباط ایجاد شده، تابع نیست.

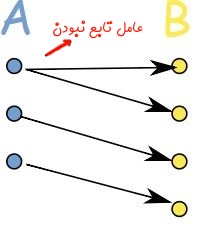
بنابراین اگر (f(x یک تابع باشد، نمی‌تواند برای یک مقدار x، همزمان دو مقدار ۷ و ۶ داشته باشد.

تابع یک به یک

به تابعی که در آن هر خروجی ناشی از فقط یک ورودی باشد، یک به یک گفته می‌شود.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

در حقیقت برای بوجود آوردن تابعی یک به یک، نمی‌توان از دو یا چند عضو از A به سمت یک B، برداری رسم کرد. در ادامه دو تابع یک به یک و غیر یک به یک نشان داده شده‌اند.

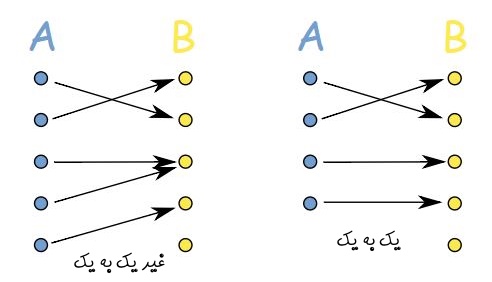
همان‌گونه که مشاهده می‌کنید در تابع سمت چپ دو عضو از مجموعه A به یک عضو از B مرتبط شده‌اند، بنابراین نمی‌تواند یک به یک باشد. از طرفی در تصویر سمت راست، هر عضو از B، تنها یک بار انتخاب شده، بنابراین تابع یک به یک است.

تابع پوشا

پوشا، به تابعی گفته می‌شود که در آن تمامی اعضای B، حداقل یک بار انتخاب شده باشند. برای درک بهتر به شکل‌های زیر توجه فرمایید. همان‌طور که در شکل سمت چپ می‌بینید یکی از اعضای مجموعه B انتخاب نشده است. بنابراین تابع سمت چپ پوشا نیست.

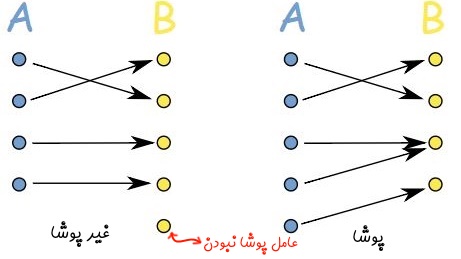
تابع یک به یک و پوشا

به تابعی که در آن تمامی اجزای A و B برای دقیقا یک بار با یکدیگر در ارتباط باشند، تابع «یک به یک و پوشا» (Bijective) گفته می‌شود.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

اگر به تعریف توجه فرمایید، تابعی که چنین ویژگی را داشته باشد، هم پوشا و هم یک به یک است. در شکل زیر نمونه‌ای از این تابع نشان داده شده است.

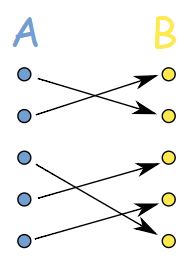
نکته مهم در توابع یک به یک و پوشا، این است که آن‌ها قطعا می‌توانند تابع معکوس داشته باشند. یعنی معکوس آن‌ها نیز خود یک تابع است.

تشخیص تابع یک به یک و پوشا

در بالا توابع یک به یک و پوشا در قالب اجزای یک مجموعه توضیح داده شدند. اما شاید این سوال برایتان پیش آمده باشد که چطور می‌توان با توجه به نمودار یک تابع، نوع آن را مشخص کرد؟ برای پاسخ به این سوال، مثال‌هایی از تشخیص نوع توابع از روی نمودارشان ارائه شده است.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

فرض کنید مقادیر A، متناظر با محور x و مقادیر B، متناظر با محور y باشد. با این فرض، نمودار ارائه شده در ادامه را در نظر بگیرد.

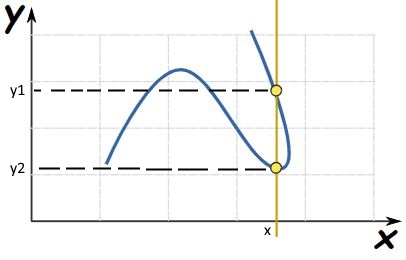
همان‌گونه که در شکل نیز مشاهده می‌کنید، اگر خطی را به صورت عمودی رسم کنید، در دو نقطه نمودار را قطع می‌کند. در حقیقت به ازای یک مقدار از x، دو مقدار از y خواهیم داشت؛ در حقیقت نمودار فوق نمی‌تواند یک تابع باشد.

نکته: به‌منظور تشخیص تابع بودن یا نبودنِ یک نمودار،‌ تمامی خطوط عمودی رسم شده، بایستی تابع را حداکثر در یک نقطه قطع کنند. می‌توان گفت شکل کلی یک تابع بایستی به‌ صورت زیر باشد.

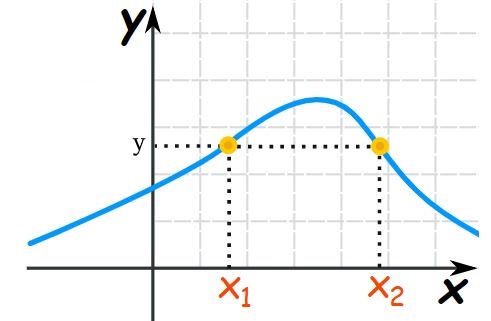
با توجه به توضیحات فوق، احتمالا نحوه تشخیص توابع یک به یک را حدس زده‌اید. به‌منظور تشخیص این نمونه از توابع، تمامی خطوط افقی گذرنده از نمودار، بایستی حداکثر آن را در یک نقطه قطع کند.

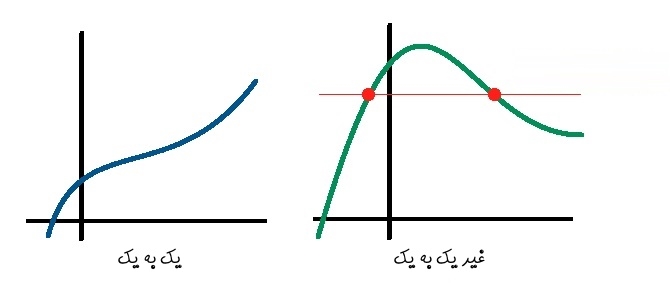
برای نمونه دو نمودار ارائه شده در بالا را در نظر بگیرید. در نمودار سمت چپ هر خط افقی نمودار را تنها در یک نقطه قطع می‌کند؛ از طرفی در نمودار سمت راست، مشاهده می‌شود که نمودار در دو نقطه قطع شده است.

بنابراین می‌توان به‌طور خلاصه گفت:

• خطوط عمودی، یک تابع را حداکثر در یک نقطه قطع می‌کنند.
• خطوط افقی، یک تابعِ یک به یک را حداکثر در یک نقطه قطع می‌کنند.

تشخیص از روی تابع

برای تشخیص تابع پوشا و یک به یک، بایستی در قدم اول دامنه و برد تابع را بدست آورید. سپس بررسی کنید و ببینید آیا به ازای دو ورودیِ متفاوت، می‌توان خروجی یکسانی داشت؟ در صورت مثبت بودن پاسخ سوال، تابع مذکور یک به یک نخواهد بود.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

عبارت فوق را می‌توان به شکلی ریاضیاتی و به صورت $$f ( x ) = f ( y ) \rightarrow x = y$$ بیان کرد. بنابراین در مواجه با یک تابع،‌ معادله (f(x)=f(y را تشکیل دهید. اگر در نتیجه‌ی این عبارت به رابطه‌ی x=y رسیدید، تابع یک به یک است؛‌ در غیر این‌ صورت تابع، یک به یک نیست. برای نمونه می‌توانید به مثال‌های زیر توجه فرمایید.

مثال ۱

تابعی را به شکل $$f ( x ) = x+5$$ به نحوی در نظر بگیرید که در مجموعه اعداد حقیقی تعریف شده باشد (f:R→R). همان‌طور که بیان شد در قدم اول بایستی (f(y را نوشته و برابری آن را با تابع (f(x بررسی کرد. بدین منظور دو تابع $$f ( x ) = x+5$$ و $$f ( y ) = y+5$$ را با یکدیگر برابر قرار می‌دهیم. در نتیجه با توجه به معادله $$x + 5 = y + 5$$، رابطه بین x و y به‌صورت x=y بدست می‌آید. در نتیجه تابع مذکور یک به یک است. این تابع می‌تواند در بازه اعداد حقیقی هر مقداری را به عنوان خروجی داشته باشد. بنابراین تابع مذکور پوشا نیز هست.

مثال ۲

تابع $$f ( x ) = x^2$$ را در بازه اعداد حقیقی در نظر بگیرید. وقتی می‌گوییم در بازه اعداد حقیقی، یعنی مجموعه A برابر با اعداد حقیقی و مجموعه B نیز برابر با کل اعداد حقیقی در نظر گرفته شده‌ است. اما این تابع تنها می‌تواند مقادیری مثبت را به‌ عنوان خروجی داشته باشد. درنتیجه -در بازه اعداد حقیقی- این تابع پوشا نیست.

از طرفی به منظور تعیین یک به یک بودن تابع، از معادله (f(x)=f(y استفاده می‌شود. با توجه به این معادله رابطه‌ی بین x و y به صورت x=±y بدست می‌آید. این رابطه می‌گوید با انتخاب x+ و x- به‌عنوان ورودی،‌ تابع یک y ثابت را به ما می‌دهد. برای نمونه با انتخاب 2+ و 2- به عنوان ورودی داریم:

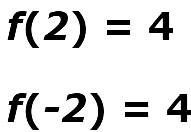
بنابراین همان‌گونه که می‌بینید به ازای دو مقدار متفاوتِ x به یک مقدار از y رسیدیم. حال این سوال مطرح می‌شود که آیا این تابع همواره غیر یک به یک و غیر پوشا است؟ پاسخ منفی است. در حقیقت اگر این تابع در مجموعه اعداد طبیعی ($$N \rightarrow N$$) تعریف شود، هم پوشا و هم یک به یک خواهد بود. بنابراین مهم است بدانید که پوشا یا یک به یک بودن یک تابع، وابسته به فضایی است که تابع روی آن تعریف می‌شود. این فضا، حاصل از دامنه و برد تابع است.