فرادرسآزمون والد (Wald Test) — مفهوم و کاربردها
در آمار و تحلیل‌های آماری، انجام آزمون فرض و انتخاب آماره آزمون مناسب، یکی از مهم‌ترین بخش‌های نظری و تئوری آمار محسوب می‌شود. آماره والد (Wald Statistics) و آزمون والد (Wald Test) یکی از این گونه مباحث است. در این نوشتار ابتدا موضوع آزمون والد را مطرح کرده و شرایط اجرای آن را بازگو می‌کنیم. سپس آماره آزمون، نحوه محاسبه و کاربردهای آن را در دیگر بخش‌های تحلیل آماری بررسی خواهیم کرد.
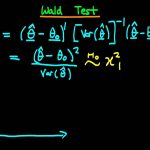
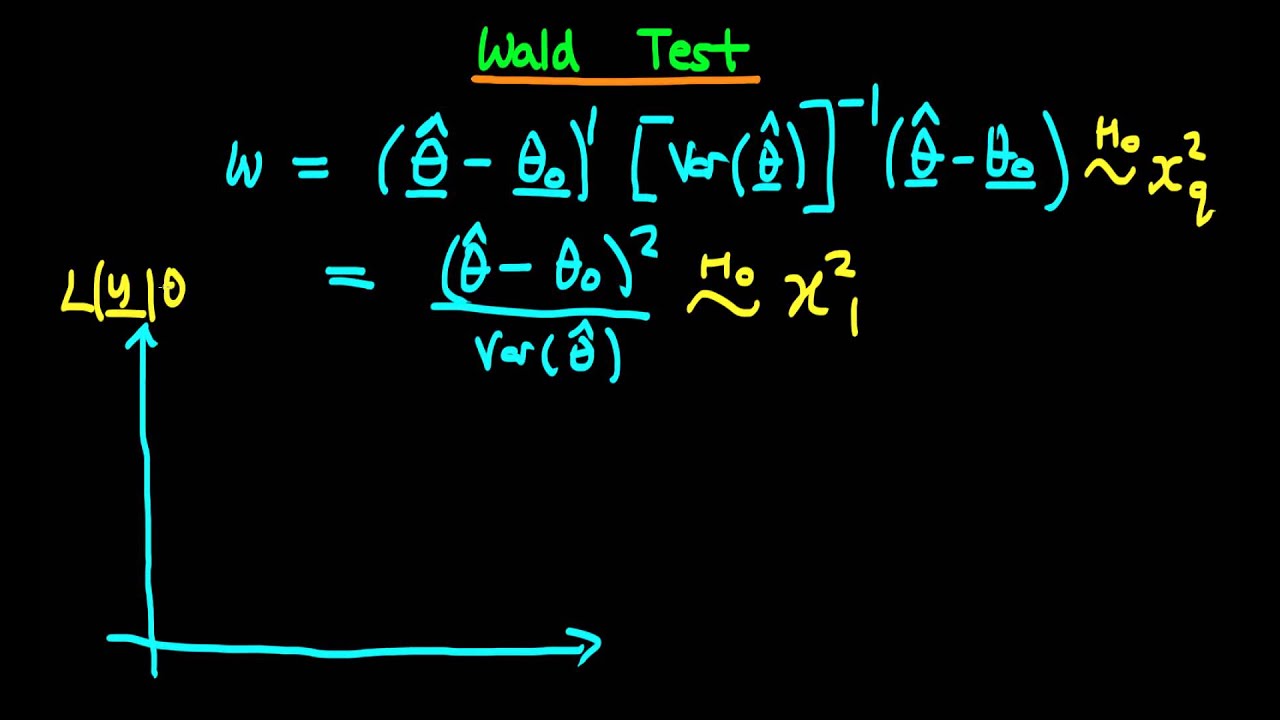
برای آشنایی با شیوه انجام آزمون فرض و اصطلاحات آن مطلب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات را مطالعه کنید. همچنین برای آگاهی از نحوه انجام آزمون مقایسه میانگین نوشتار آزمون فرض میانگین جامعه در آمار — به زبان ساده را بخوانید. همچنین مطالعه تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده نیز خالی از لطف نیست.
آزمون والد و آماره والد (Wald Test)
«آزمون والد» (Wald Test) به عنوان یک آزمون‌های پارامتری در نظر گرفته می‌شود زیرا به توزیع داده‌ها نیاز دارد. این آزمون به افتخار دانشمند آمار و ریاضی‌دان مجارستانی «آبراهام والد» انتخاب شده است.
او این روش را برای آزمون کردن برابری پارامتر جامعه ($$\theta$$) با یک مقدار ثابت ($$\theta_0$$) ایجاد کرد.
فرض کنید که برآورد حداکثر درستنمایی یا (MLE (Maximum Likelihood Estimator پارامتر $$\theta$$ به صورت $$\widehat{\theta}$$ باشد. همچنین اگر $$\theta_0$$ برآوردگر حدسی باشد، با فرض نرمال بودن اختلاف بین این دو، می‌توان توزیع کسر زیر را کای-۲ در نظر گرفت.
$$\large W=\dfrac{(\widehat{\theta}-\theta_0)^2}{Var(\hat{\theta)}}$$
به این ترتیب اگر مقدار $$W$$ بیشتر از مقدار چندک $$\alpha$$ام توزیع کای-۲ با یک درجه آزادی باشد، فرض صفر که به صورت زیر نوشته می‌شود، در سطح خطای $$\alpha$$ رد خواهد شد.
$$\large \begin{cases} H_0: \theta =\theta_0 \\ \large H_1: \theta \neq \theta_0\\ \end{cases}$$
همانطور که دیده می‌شود، این آماره و آزمون در حالت یک بعدی به کار می‌روند. در ادامه به حالت چند بعدی این آزمون خواهیم پرداخت.
آزمون همزمان والد روی چندین پارامتر (Wald Test on Multiple Parameters)
از آزمون والد می‌توان برای انجام آزمون تکی بر روی چندین پارامتر یا آزمون‌های همزمان ترکیب یک یا چند پارامتر استفاده کرد. فرض کنید که بردار $$\widehat{\theta}$$ برآوردگرهای p پارامتر باشند. به این ترتیب $$\widehat{\theta}$$ یک بردار $$p\times 1$$ بوده که برآوردگر درستنمایی برای بردار پارامترهای $$\theta$$ است.
فرض می‌شود که این بردار برآوردگرها، دارای توزیع نرمال چند متغیره با بردار میانگین $$\theta$$ و ماتریس کوواریانس $$V$$ است. در نتیجه رابطه زیر را خواهیم داشت.
$$\large \sqrt {n}({\hat {\theta }}_{n}-\theta ){\xrightarrow {\mathcal {D}}}N(0,V)$$
این رابطه به این معنی است که طرف راست در توزیع به نرمال چند متغیره با بردار میانگین صفر و ماتریس کوواریانس $$V$$ میل می‌کند. حال فرض کنید که Q تعداد آزمونی‌هایی باشد که روی P پارامتر صورت خواهد گرفت. این آزمون ها را به کمک یک ماتریس به نام R که دارای Q سطر و P ستون است معرفی می‌کنیم. به این ترتیب فرضیات آزمون به صورت زیر نوشته خواهند شد.
$$\large \begin{cases} H_0: R\theta =\theta_0 \\ \large H_1: R\theta \neq \theta_0\\ \end{cases}$$
برای مثال فرض کنید که برای یک بردار با ۳ سطر از پارامترها می‌خواهید آزمون والد را اجرا کنید. در این صورت ماتریس R، بردار $$\theta_0$$ و بردار $$\theta$$ به شکل زیر نوشته خواهند شد. با در نظر گرفتن این ماتریس و بردارها، مقایسه سه پارامتر با مقدار ثابت انجام خواهد گرفت.
| بردار پارامترها$$\theta$$ | بردار مقادیر حدسی $$\theta_0$$ | ماتریس R |
| $$\large \theta=\begin{bmatrix}\theta_1\\ \theta_2\\ \theta_3\\ \end{bmatrix}$$ |
$$\large \theta_0=\begin{bmatrix} \theta_{0_1}\\ \theta_{0_2}\\ \theta_{0_3}\\ \end{bmatrix} $$ |
$$\large R=\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ \end{bmatrix}$$ |
در این حالت آماره آزمون به صورت زیر نوشته خواهد شد. مشخص است که این آماره دارای توزیع کای ۲ با Q درجه آزادی است.
$$ \large (R{\hat {\theta }}_{n}-r)^{T}[R({\hat {V}}_{n}/n)R^{'}]^{-1}(R{\hat {\theta }}_{n}-r)\quad {\xrightarrow {\mathcal {D}}}\quad \chi _{Q}^{2}$$
مشخص است که در این جا $$\hat{V_n}$$ برآوردگر ماتریس کوواریانس برای $$\hat{\theta}$$ است.
کاربردها
هنگام استفاده از آزمون فرض مربوط به میانگین جامعه، به جای آزمون و آماره T می‌توان از آماره والد استفاده کرد. همچنین در بعضی از روش‌های رگرسیونی، زمانی که احتیاج به انجام آزمون روی ضرایب رگرسیونی لازم است، آزمون والد مفید به نظر می‌رسد. بخصوص اگر برآوردگر پارامتر براساس حداکثر تابع درستنمایی حاصل شده باشد. برای مثال در رگرسیون لجستیک از آنجایی که برآورد پارامترهای مدل رگرسیون، توسط برآوردگرهای حداکثر درستنمایی بدست می‌آیند، انجام آزمون برای ضرایب مدل رگرسیونی توسط آزمون والد صورت می‌گیرد. بنابراین در بیشتر نرم‌افزار محاسبات آماری در خروجی رگرسیون لجستیک، آماره والد به همراه Sig یا همان p-value مربوط به آزمون، ظاهر می‌شود و کاربر می‌تواند نسبت به رد فرض صفر که نشانه بی‌اثر بودن آن متغیر در مدل رگرسیون لجستیک است، تصمیم بگیرد.
اگر مطلب بالا برای شما مفید بوده است و به یادگیری مباحث مشابه آن علاقه‌مند هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های SPSS
- آموزش آمار و احتمال مهندسی
- مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
- آزمایش تصادفی، پیشامد و تابع احتمال
- مجموعه آموزش‌های نرم‌افزارهای آماری
- جامعه آماری — انواع داده و مقیاس‌های آن‌ها
- تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
^^
